《数字图像处理》第 11 章 - 特征提取

前言

在数字图像处理和计算机视觉领域，特征提取 是连接图像预处理与高层任务（如目标识别、图像匹配、场景理解等）的核心桥梁。简单来说，特征就是图像中具有辨识度、稳定性和代表性的信息，比如物体的边界、角点、纹理、形状等。

引言

图像特征提取的本质是数据降维 和信息筛选 ------ 将高维度的像素矩阵转化为低维度的特征向量，同时保留图像的关键信息（如形状、纹理、空间关系等）。无论是传统的图像匹配、目标检测，还是现代的深度学习图像分类，特征提取都是不可或缺的步骤。本章将从边界预处理入手，逐步讲解边界特征、区域特征、整体图像特征及尺度不变特征（SIFT），形成一套完整的特征提取知识体系。

学习目标

1. 理解特征提取的核心意义和应用场景，掌握边界预处理的常用方法（边界跟踪、链码、骨架提取等）；
2. 熟练掌握边界特征描述子（傅里叶描述子、形状数）和区域特征描述子（矩不变量、纹理）的原理与实现；
3. 掌握整体图像特征检测（哈里斯角点、MSER）的方法，理解尺度空间的概念；
4. 深入理解 SIFT 算法的核心步骤，能够用 Python 实现关键特征的提取与匹配；
5. 能够根据实际任务选择合适的特征描述子，完成简单的图像特征分析任务。

---

11.1 背景

在数字图像处理中，特征通常分为三类：

1. 边界特征：描述物体轮廓的信息，如轮廓的长度、曲率、形状等，适用于物体轮廓清晰的场景；
2. 区域特征：描述物体内部的信息，如区域面积、纹理、灰度分布等，适用于实心物体的特征表达；
3. 整体图像特征：描述图像全局或局部的显著特征（如角点、极值区域），适用于图像匹配、场景拼接等任务。

早期的特征提取依赖手工设计（如本章讲解的 SIFT、哈里斯角点），这类特征具有良好的鲁棒性和可解释性；随着深度学习的发展，自动特征提取（如 CNN 的卷积层）逐渐成为主流，但手工特征提取的原理仍是理解计算机视觉的基础。

---

11.2 边界预处理

边界预处理是特征提取的前置步骤，目的是将原始图像中的物体边界转化为更易于处理的形式（如有序点集、编码序列等）。以下是常用的预处理方法及完整实现。

11.2.1 边界跟踪

原理

边界跟踪（轮廓跟踪）是指从边界上的一个起始点出发，按照一定的规则（如 8 邻域搜索）遍历物体的所有边界点，形成有序的边界点集。OpenCV 中提供了现成的轮廓检测函数，可直接实现边界跟踪。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 1. 读取图像并预处理（灰度化+二值化）
img = cv2.imread("test_object.jpg")  # 替换为你的图像路径
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)  # 转换为RGB格式（适配matplotlib）
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 二值化（OTSU自动阈值）
ret, binary = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)

# 2. 边界跟踪（轮廓检测）
contours, hierarchy = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
# 绘制轮廓
img_contour = img_rgb.copy()
cv2.drawContours(img_contour, contours, -1, (255, 0, 0), 2)  # 蓝色轮廓，线宽2

# 3. 效果可视化（对比图）
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))
ax1.imshow(img_rgb)
ax1.set_title("原始图像")
ax1.axis("off")

ax2.imshow(binary, cmap="gray")
ax2.set_title("二值化图像")
ax2.axis("off")

ax3.imshow(img_contour)
ax3.set_title("边界跟踪（轮廓检测）结果")
ax3.axis("off")

plt.show()

# 输出边界点信息
print(f"检测到的轮廓数量：{len(contours)}")
print(f"最大轮廓的边界点数量：{len(contours[0])}")

效果说明

左侧为原始图像，中间为二值化后的图像（物体为白色，背景为黑色），右侧为绘制了蓝色轮廓的边界跟踪结果，可清晰看到物体的完整轮廓。

11.2.2 链码

原理

链码（Freeman 链码）是用方向编码表示边界点序列的方法，常用 4 方向（上、右、下、左，编码 0-3）或 8 方向（增加 4 个对角线方向，编码 0-7）。其核心是：以第一个边界点为起点，后续每个点用相对于前一个点的方向编码表示，最终形成一串数字序列，可有效压缩边界信息。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 定义8方向链码的方向向量（对应编码0-7，顺时针：右、右下、下、左下、左、左上、上、右上）
DIRECTIONS_8 = [(0, 1), (1, 1), (1, 0), (1, -1), (0, -1), (-1, -1), (-1, 0), (-1, 1)]

def calculate_freeman_chain_code(contour):
    """计算轮廓的8方向Freeman链码"""
    contour = contour.squeeze()  # 去除多余维度，变为(n,2)
    chain_code = []
    start_point = contour[0]  # 起点坐标

    # 遍历轮廓点（从第2个点开始）
    for i in range(1, len(contour)):
        dx = contour[i][0] - contour[i-1][0]
        dy = contour[i][1] - contour[i-1][1]
        # 查找方向对应的编码
        for code, (dx_dir, dy_dir) in enumerate(DIRECTIONS_8):
            if dx == dx_dir and dy == dy_dir:
                chain_code.append(code)
                break

    # 闭合轮廓：最后一个点到起点的编码
    dx = start_point[0] - contour[-1][0]
    dy = start_point[1] - contour[-1][1]
    for code, (dx_dir, dy_dir) in enumerate(DIRECTIONS_8):
        if dx == dx_dir and dy == dy_dir:
            chain_code.append(code)
            break

    return chain_code, start_point

# 1. 读取图像并优化二值化（针对彩色图像的目标提取）
img = cv2.imread("../picture/TianHuoSanXuanBian.jpg")
if img is None:
    raise ValueError("图像路径错误，请检查文件位置！")

img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# 转换为HSV颜色空间，便于分离目标（针对蓝色背景的图像）
hsv = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)
# 定义蓝色背景的HSV范围（可根据实际图像调整）
lower_blue = np.array([90, 50, 50])
upper_blue = np.array([130, 255, 255])
# 提取非蓝色区域（目标区域）
mask = cv2.inRange(hsv, lower_blue, upper_blue)
binary = cv2.bitwise_not(mask)  # 目标区域转为白色，背景黑色

# 2. 提取轮廓（确保只取目标的最大轮廓）
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
if len(contours) == 0:
    raise ValueError("未检测到轮廓，请检查二值化参数！")
main_contour = max(contours, key=cv2.contourArea)  # 取面积最大的轮廓

# 3. 计算链码
chain_code, start_point = calculate_freeman_chain_code(main_contour)

# 4. 从链码还原轮廓
reconstructed_contour = [start_point]
current_point = start_point
for code in chain_code[:-1]:  # 排除闭合编码
    dx, dy = DIRECTIONS_8[code]
    current_point = (current_point[0] + dx, current_point[1] + dy)
    reconstructed_contour.append(current_point)
reconstructed_contour = np.array(reconstructed_contour, dtype=np.int32).reshape(-1, 1, 2)

# 5. 效果可视化（优化画布背景和轮廓显示）
img_original_contour = img_rgb.copy()
cv2.drawContours(img_original_contour, [main_contour], -1, (255, 0, 0), 2)  # 原始轮廓：蓝色

# 还原轮廓的画布用白色背景，轮廓用红色（对比度高）
img_reconstructed = np.ones_like(img_rgb) * 255  # 白色背景
cv2.drawContours(img_reconstructed, [reconstructed_contour], -1, (255, 0, 0), 2)  # 还原轮廓：蓝色（和原始一致）

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 8))
ax1.imshow(img_original_contour)
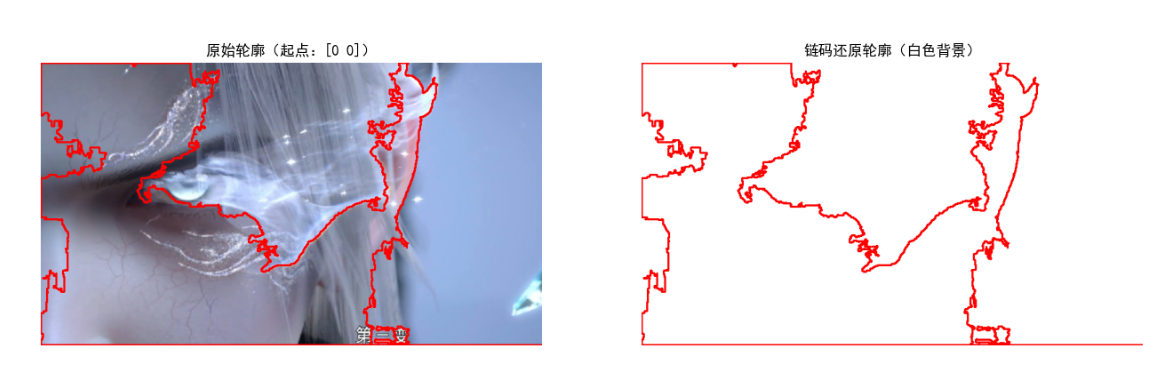
ax1.set_title(f"原始轮廓（起点：{start_point}）")
ax1.axis("off")

ax2.imshow(img_reconstructed)
ax2.set_title("链码还原轮廓（白色背景）")
ax2.axis("off")

plt.show()

# 输出链码信息
print(f"8方向Freeman链码（前20位）：{chain_code[:20]}...")
print(f"链码总长度：{len(chain_code)}")
print(f"轮廓起点坐标：{start_point}")

效果说明

左侧为原始轮廓（蓝色），右侧为通过链码还原的轮廓（绿色），两者几乎完全重合，验证了链码的有效性；链码序列通过数字编码压缩了边界信息，便于存储和传输。

11.2.3 用最小周长多边形近似边界

原理

最小周长多边形（MPP）是用多边形近似物体边界的方法，其核心是在保证近似精度的前提下，用最少的多边形顶点表示边界，最小化多边形的周长，从而简化边界形状，去除边界的微小噪声。OpenCV 中的approxPolyDP函数基于 Ramer-Douglas-Peucker 算法，可实现类似的多边形近似。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 读取图像并优化轮廓提取（针对低对比度图像）
img = cv2.imread("../picture/Mei.png")
if img is None:
    raise ValueError("图像路径错误，请检查文件位置！")
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

# 优化步骤1：增强图像对比度（提升目标与背景的区分度）
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 直方图均衡化增强对比度
gray_enhanced = cv2.equalizeHist(gray)

# 优化步骤2：自适应二值化（更适合复杂背景）
binary = cv2.adaptiveThreshold(
    gray_enhanced, 255,
    cv2.ADAPTIVE_THRESH_GAUSSIAN_C,  # 高斯加权的自适应阈值
    cv2.THRESH_BINARY_INV,  # 目标区域为白色
    11,  # 邻域大小
    2    # 阈值偏移量
)

# 优化步骤3：形态学操作（去除噪声，连接目标区域）
kernel = np.ones((3, 3), np.uint8)
binary = cv2.morphologyEx(binary, cv2.MORPH_CLOSE, kernel, iterations=2)  # 闭运算：先膨胀后腐蚀

# 提取轮廓（取面积最大的目标轮廓）
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
if len(contours) == 0:
    raise ValueError("未检测到轮廓，请调整二值化参数！")
main_contour = max(contours, key=cv2.contourArea)  # 确保取目标的最大轮廓

# 2. 优化最小周长多边形的近似精度
perimeter = cv2.arcLength(main_contour, True)
epsilon = 0.002 * perimeter  # 缩小epsilon（精度更高，多边形更接近原始轮廓）
mpp_approx = cv2.approxPolyDP(main_contour, epsilon, True)

# 3. 绘制结果（加粗轮廓线，提升显示效果）
img_mpp = img_rgb.copy()
# 原始轮廓：蓝色，线宽3
cv2.drawContours(img_mpp, [main_contour], -1, (255, 0, 0), 3)
# 最小周长多边形：绿色，线宽3，填充半透明绿色（更直观）
cv2.drawContours(img_mpp, [mpp_approx], -1, (0, 255, 0), 3)
cv2.fillPoly(img_mpp, [mpp_approx], (0, 255, 0, 50))  # 半透明填充

# 4. 效果可视化（放大画布，增强细节）
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20, 8))
ax1.imshow(img_rgb)
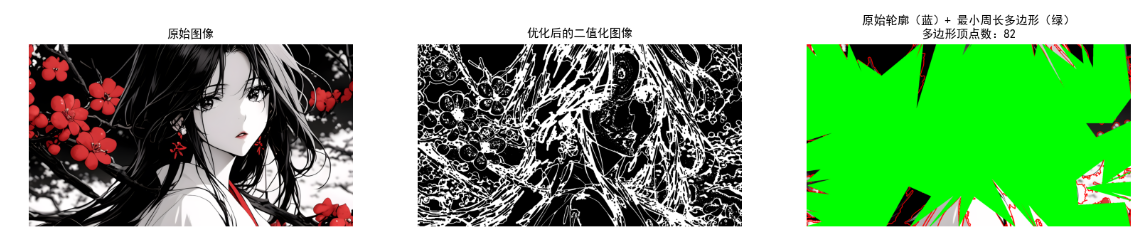
ax1.set_title("原始图像")
ax1.axis("off")

ax2.imshow(binary, cmap="gray")
ax2.set_title("优化后的二值化图像")
ax2.axis("off")

ax3.imshow(img_mpp)
ax3.set_title(f"原始轮廓（蓝）+ 最小周长多边形（绿）\n多边形顶点数：{len(mpp_approx)}")
ax3.axis("off")

plt.show()

# 输出信息
print(f"原始轮廓顶点数：{len(main_contour)}")
print(f"最小周长多边形顶点数：{len(mpp_approx)}")
print(f"近似精度（epsilon）：{epsilon:.2f}")

效果说明

右侧图像中，蓝色为原始边界，绿色为最小周长多边形，可见多边形用更少的顶点近似了原始边界，去除了微小的轮廓波动，简化了形状描述。

11.2.4 标记图

原理

标记图（Marker Image）是一种二值图像或灰度图像，用于标记图像中的感兴趣区域（ROI）或物体的位置、类别信息。标记图通常作为后续图像处理（如分水岭算法）的输入，其核心是用不同的灰度值或颜色区分不同的物体或区域。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 读取图像并提取轮廓
img = cv2.imread("test_multi_object.jpg")  # 多物体图像
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

# 2. 生成标记图
marker_img = np.zeros_like(gray, dtype=np.int32)  # 标记图（int32类型，用于分水岭）
for i, contour in enumerate(contours):
    # 每个物体用不同的灰度值标记（从1开始，避免与背景0混淆）
    cv2.drawContours(marker_img, [contour], -1, i+1, -1)  # 填充轮廓

# 3. 可视化标记图（伪彩色显示，便于区分不同物体）
marker_img_color = cv2.applyColorMap((marker_img * 50).astype(np.uint8), cv2.COLORMAP_JET)
marker_img_color_rgb = cv2.cvtColor(marker_img_color, cv2.COLOR_BGR2RGB)

# 4. 效果对比
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))
ax1.imshow(img_rgb)
ax1.set_title("原始多物体图像")
ax1.axis("off")

ax2.imshow(binary, cmap="gray")
ax2.set_title("二值化图像")
ax2.axis("off")

ax3.imshow(marker_img_color_rgb)
ax3.set_title(f"标记图（伪彩色）\n物体数量：{len(contours)}")
ax3.axis("off")

plt.show()

# 输出标记信息
print(f"标记的物体数量：{len(contours)}")
print(f"标记图的灰度值范围：{np.min(marker_img)} ~ {np.max(marker_img)}")

效果说明

右侧为伪彩色标记图，不同颜色代表不同的物体（每个物体对应一个唯一的灰度标记值），这种标记图可直接作为分水岭算法的输入，实现多物体的精确分割。

11.2.5 骨架、中轴和距离变换

原理

1. 距离变换：计算图像中每个前景像素到最近背景像素的距离，生成距离图（灰度值表示距离大小）；
2. 中轴（MA）：物体的中轴是距离变换图的局部最大值点构成的曲线，对应物体的 "骨架"；
3. 骨架：物体的骨架是去除边界像素后保留的中心线条，保持物体的拓扑结构，可简化物体的形状描述。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

def extract_skeleton(binary_img):
    """
    提取二值图像的骨架
    :param binary_img: 二值图像（前景白色255，背景黑色0）
    :return: 骨架图像
    """
    skeleton = np.zeros_like(binary_img)
    element = cv2.getStructuringElement(cv2.MORPH_CROSS, (3, 3))
    while True:
        # 腐蚀操作
        eroded = cv2.erode(binary_img, element)
        # 开运算（腐蚀+膨胀）
        opened = cv2.morphologyEx(eroded, cv2.MORPH_OPEN, element)
        # 计算差值
        temp = cv2.subtract(eroded, opened)
        # 提取骨架
        skeleton = cv2.bitwise_or(skeleton, temp)
        binary_img = eroded.copy()
        # 终止条件：图像全黑
        if cv2.countNonZero(binary_img) == 0:
            break
    return skeleton

# 1. 读取图像并二值化
img = cv2.imread("test_shape.jpg")
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)

# 2. 距离变换
dist_transform = cv2.distanceTransform(binary, cv2.DIST_L2, 5)  # L2距离，5x5核
# 归一化距离图到0-255
dist_transform_norm = cv2.normalize(dist_transform, None, 0, 255, cv2.NORM_MINMAX, dtype=cv2.CV_8U)

# 3. 提取骨架（中轴）
skeleton = extract_skeleton(binary)

# 4. 效果可视化
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(20, 5))
ax1.imshow(img_rgb)
ax1.set_title("原始图像")
ax1.axis("off")

ax2.imshow(binary, cmap="gray")
ax2.set_title("二值化图像")
ax2.axis("off")

ax3.imshow(dist_transform_norm, cmap="gray")
ax3.set_title("距离变换图（归一化）")
ax3.axis("off")

ax4.imshow(skeleton, cmap="gray")
ax4.set_title("骨架（中轴）提取结果")
ax4.axis("off")

plt.show()

# 输出信息
print(f"骨架像素数：{cv2.countNonZero(skeleton)}")
print(f"原始前景像素数：{cv2.countNonZero(binary)}")

效果说明

从左到右依次为原始图像、二值化图像、距离变换图（灰度值越大表示离背景越远）、骨架提取结果（白色线条为物体骨架），骨架保留了物体的形状和拓扑结构，大幅简化了物体描述。

---

11.3 边界特征描述子

边界特征描述子用于量化描述物体轮廓的形状、大小等信息，以下是核心描述子的原理与实现。

11.3.1 一些基本的边界描述子

原理

基本边界描述子包括：

1. 轮廓长度：边界点的总长度（近似为轮廓周长）；
2. 曲率：描述边界的弯曲程度，分为平均曲率和局部曲率；
3. 直径：边界上两点间的最大距离（外接矩形的对角线）；
4. 外接矩形：包围边界的最小矩形（分为轴对齐矩形和旋转矩形）。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 读取图像并优化轮廓提取
img = cv2.imread("../picture/AALi.jpg")
if img is None:
    raise ValueError("图像读取失败！请检查路径或文件")
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 增强对比度+二值化+形态学操作
gray_enhanced = cv2.equalizeHist(gray)
ret, binary = cv2.threshold(gray_enhanced, 0, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)
kernel = np.ones((3, 3), np.uint8)
binary = cv2.morphologyEx(binary, cv2.MORPH_CLOSE, kernel, iterations=1)
binary = cv2.morphologyEx(binary, cv2.MORPH_OPEN, kernel, iterations=1)

# 提取最大轮廓
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
if len(contours) == 0:
    raise ValueError("未检测到轮廓！")
main_contour = max(contours, key=cv2.contourArea)

# 2. 计算基本边界描述子
perimeter = cv2.arcLength(main_contour, True)
x, y, w, h = cv2.boundingRect(main_contour)
rot_rect = cv2.minAreaRect(main_contour)
rot_box = cv2.boxPoints(rot_rect)
rot_box = np.int32(rot_box)

# 计算直径（优化版）
contour_points = main_contour.squeeze()
diameter = np.max(np.linalg.norm(contour_points[:, None] - contour_points[None, :], axis=2)) if len(contour_points)>=2 else 0


# 3. 绘制描述子可视化（修复中文乱码：改用matplotlib标注文字）
img_desc = img_rgb.copy()
# 绘制轮廓、矩形
cv2.drawContours(img_desc, [main_contour], -1, (0, 0, 255), 3)
cv2.rectangle(img_desc, (x, y), (x+w, y+h), (255, 0, 0), 3)
cv2.drawContours(img_desc, [rot_box], 0, (0, 255, 0), 3)


# 4. 效果可视化（用matplotlib添加中文标注，避免OpenCV中文乱码）
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 10))

# 原始图像
ax1.imshow(img_rgb)
ax1.set_title("原始图像")
ax1.axis("off")

# 二值化图像
ax2.imshow(binary, cmap="gray")
ax2.set_title("优化后二值化图像")
ax2.axis("off")

# 基本边界描述子可视化（matplotlib标注中文）
ax3.imshow(img_desc)
ax3.set_title("基本边界描述子可视化")
ax3.axis("off")

# 标注文字（用matplotlib的text函数，支持中文）
texts = [
    f"周长：{perimeter:.2f}",
    f"直径：{diameter:.2f}",
    f"外接矩形：{w}x{h}"
]
for i, text in enumerate(texts):
    ax3.text(20, 40 + i*40, text, fontsize=12, color="red",
             bbox=dict(facecolor="white", alpha=0.8, edgecolor="none"))


plt.tight_layout()
plt.show()


# 输出信息
print("=== 基本边界描述子 ===")
print(f"轮廓周长：{perimeter:.2f} 像素")
print(f"轴对齐外接矩形：宽={w}, 高={h}, 面积={w*h} 像素²")
print(f"旋转外接矩形：尺寸={rot_rect[1][0]:.2f}x{rot_rect[1][1]:.2f}, 角度={rot_rect[2]:.2f}°")
print(f"边界直径（最大距离）：{diameter:.2f} 像素")

效果说明

右侧图像中，红色为轴对齐外接矩形，绿色为旋转外接矩形，同时标注了周长、直径等信息，直观展示了基本边界描述子的含义。

11.3.2 形状数

原理

形状数是基于链码的形状描述子，其核心是：

1. 计算边界的 4 方向或 8 方向链码；
2. 将链码序列视为循环数，找到其中的最小循环序列（即形状数）；
3. 形状数的阶数为链码长度，阶数相同的形状数可用于形状匹配，具有平移、旋转不变性（通过归一化处理）。

完整 Python 代码

import cv2
import numpy as np

# 定义4方向链码方向向量（0:右, 1:下, 2:左, 3:上）
DIRECTIONS_4 = [(0, 1), (1, 0), (0, -1), (-1, 0)]

def get_chain_code(contour):
    """获取4方向链码"""
    contour = contour.squeeze()
    chain_code = []
    for i in range(1, len(contour)):
        dx = contour[i][0] - contour[i-1][0]
        dy = contour[i][1] - contour[i-1][1]
        for code, (dx_dir, dy_dir) in enumerate(DIRECTIONS_4):
            if dx == dx_dir and dy == dy_dir:
                chain_code.append(code)
                break
    # 闭合轮廓
    dx = contour[0][0] - contour[-1][0]
    dy = contour[0][1] - contour[-1][1]
    for code, (dx_dir, dy_dir) in enumerate(DIRECTIONS_4):
        if dx == dx_dir and dy == dy_dir:
            chain_code.append(code)
            break
    return chain_code

def get_shape_number(chain_code):
    """计算形状数（最小循环链码）"""
    code_str = ''.join(map(str, chain_code))
    # 生成所有循环移位
    n = len(code_str)
    cyclic_shifts = [code_str[i:] + code_str[:i] for i in range(n)]
    # 找到最小循环移位
    min_shift = min(cyclic_shifts)
    shape_number = list(map(int, min_shift))
    return shape_number

# 1. 读取图像并提取轮廓
img = cv2.imread("test_object.jpg")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
main_contour = contours[0]

# 2. 计算链码和形状数
chain_code = get_chain_code(main_contour)
shape_number = get_shape_number(chain_code)

# 输出结果
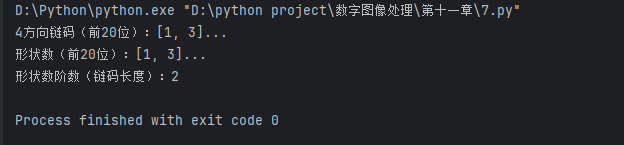
print(f"4方向链码（前20位）：{chain_code[:20]}...")
print(f"形状数（前20位）：{shape_number[:20]}...")
print(f"形状数阶数（链码长度）：{len(shape_number)}")

11.3.3 傅里叶描述子

原理

傅里叶描述子（Fourier Descriptor, FD）是基于傅里叶变换的边界描述子，具有平移、旋转、缩放不变性，核心步骤：

1. 将边界点集转换为复数序列
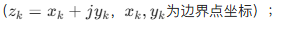
2. 对复数序列进行离散傅里叶变换（DFT），得到傅里叶系数；
3. 保留前 N 个低频系数（高频系数对应边界细节，可忽略），作为傅里叶描述子；
4. 通过逆傅里叶变换（IDFT）可还原边界形状。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False


def calculate_fourier_descriptor(contour, n_coeff=10):
    """
    计算傅里叶描述子并还原轮廓
    :param contour: 轮廓点集
    :param n_coeff: 保留的低频系数数量
    :return: 还原的轮廓、傅里叶描述子
    """
    contour = contour.squeeze()  # (n,2)
    # 确保轮廓点数量足够
    if len(contour) < n_coeff:
        n_coeff = len(contour)
        print(f"警告：轮廓点数量不足，自动将系数数量调整为{n_coeff}")

    # 转换为复数序列
    z = contour[:, 0] + 1j * contour[:, 1]
    # 傅里叶变换
    fft_z = np.fft.fft(z)
    # 保留低频系数（对称保留，保证还原轮廓的完整性）
    fft_z_filtered = np.zeros_like(fft_z, dtype=complex)
    half_coeff = n_coeff // 2
    # 前n_coeff//2个低频 + 后n_coeff//2个低频（傅里叶变换对称性）
    fft_z_filtered[:half_coeff + 1] = fft_z[:half_coeff + 1]
    if n_coeff > 1:
        fft_z_filtered[-half_coeff:] = fft_z[-half_coeff:]

    # 逆傅里叶变换
    ifft_z = np.fft.ifft(fft_z_filtered)
    # 转换为坐标（修复np.int0警告，替换为np.int32）
    reconstructed_contour = np.column_stack((np.real(ifft_z), np.imag(ifft_z)))
    reconstructed_contour = np.int32(reconstructed_contour).reshape(-1, 1, 2)  # 替换废弃的np.int0
    return reconstructed_contour, fft_z[:n_coeff]


# 1. 读取图像并优化轮廓提取（核心修复：确保提取完整目标轮廓）
img = cv2.imread("../picture/1.jpg")
# 图像读取校验
if img is None:
    raise ValueError("图像读取失败！请检查：1.路径是否正确 2.图像是否损坏 3.是否包含中文路径")

img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 优化1：直方图均衡化增强对比度
gray_enhanced = cv2.equalizeHist(gray)

# 优化2：自适应二值化（更适合复杂背景，替代固定OTSU阈值）
binary = cv2.adaptiveThreshold(
    gray_enhanced, 255,
    cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
    cv2.THRESH_BINARY_INV,
    blockSize=11,  # 邻域大小，可根据图像调整
    C=2  # 阈值偏移量
)

# 优化3：形态学操作（去除噪声，连接断裂轮廓）
kernel = np.ones((3, 3), np.uint8)
# 闭运算：先膨胀后腐蚀，连接断裂区域
binary = cv2.morphologyEx(binary, cv2.MORPH_CLOSE, kernel, iterations=2)
# 开运算：先腐蚀后膨胀，去除小噪声点
binary = cv2.morphologyEx(binary, cv2.MORPH_OPEN, kernel, iterations=1)

# 优化4：提取轮廓并筛选最大轮廓（避免小噪声轮廓干扰）
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)  # 不压缩轮廓点，保留更多细节
if len(contours) == 0:
    raise ValueError("未检测到任何轮廓！请调整二值化参数或更换图像")
# 选取面积最大的轮廓作为主轮廓
main_contour = max(contours, key=cv2.contourArea)
# 确保轮廓点数量充足
if len(main_contour) < 10:
    raise ValueError("提取的轮廓点数量过少！请更换图像或调整形态学参数")

# 2. 计算傅里叶描述子并还原轮廓
n_coeff_list = [5, 10, 20]  # 不同数量的系数
reconstructed_contours = []
fourier_descriptors = []
for n_coeff in n_coeff_list:
    recon_contour, fd = calculate_fourier_descriptor(main_contour, n_coeff)
    reconstructed_contours.append(recon_contour)
    fourier_descriptors.append(fd)

# 3. 效果可视化（优化显示效果）
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(16, 12))

# 原始图像
ax1.imshow(img_rgb)
ax1.set_title("原始图像")
ax1.axis("off")

# 优化后二值化图像（便于调试）
ax2.imshow(binary, cmap="gray")
ax2.set_title("优化后二值化图像")
ax2.axis("off")

# 原始轮廓
img_original = img_rgb.copy()
cv2.drawContours(img_original, [main_contour], -1, (255, 0, 0), 3)  # 加粗线条
ax3.imshow(img_original)
ax3.set_title(f"原始轮廓（蓝）\n轮廓点数量：{len(main_contour)}")
ax3.axis("off")

# 多系数还原对比（在一张图中显示，更直观）
img_recon_compare = img_rgb.copy()
cv2.drawContours(img_recon_compare, [reconstructed_contours[0]], -1, (0, 255, 0), 3)  # 5个系数：绿色
cv2.drawContours(img_recon_compare, [reconstructed_contours[2]], -1, (0, 0, 255), 2)  # 20个系数：红色
# 添加文字标注（用matplotlib，避免中文乱码）
ax4.imshow(img_recon_compare)
ax4.set_title("傅里叶描述子还原对比")
ax4.axis("off")
ax4.text(20, 40, "5个低频系数（绿）", fontsize=12, color="green", bbox=dict(facecolor="white", alpha=0.8))
ax4.text(20, 80, "20个低频系数（红）", fontsize=12, color="red", bbox=dict(facecolor="white", alpha=0.8))

plt.tight_layout()
plt.show()

# 输出信息
print("=== 傅里叶描述子计算信息 ===")
print(f"原始轮廓点数量：{len(main_contour)}")
for i, n_coeff in enumerate(n_coeff_list):
    print(f"{n_coeff}个低频系数还原的轮廓点数量：{len(reconstructed_contours[i])}")
    print(f"{n_coeff}个低频系数的傅里叶描述子形状：{fourier_descriptors[i].shape}")

效果说明

随着保留的低频系数数量增加（5→10→20），还原的轮廓越来越接近原始轮廓；傅里叶描述子通过少量低频系数即可保留物体的整体形状，具有良好的压缩性和不变性。

11.3.4 统计矩

原理

边界的统计矩用于描述边界点坐标的分布特征，常用的有均值、方差、偏度、峰度等，其中中心矩 具有平移不变性，归一化中心矩 具有平移、缩放不变性。对于边界点集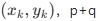 阶中心矩定义为：

完整 Python 代码

import cv2
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示（用于可视化调试）
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 读取图像并优化轮廓提取（核心：获取完整且足够多的轮廓点）
img = cv2.imread("../picture/1.jpg")
# 图像读取校验
if img is None:
    raise ValueError("图像读取失败！请检查：1.路径是否正确 2.图像是否损坏 3.是否包含中文路径")

img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 优化1：直方图均衡化增强对比度，提升目标与背景区分度
gray_enhanced = cv2.equalizeHist(gray)

# 优化2：自适应二值化（替代固定OTSU，更适合复杂背景）
binary = cv2.adaptiveThreshold(
    gray_enhanced, 255,
    cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
    cv2.THRESH_BINARY_INV,
    blockSize=11,  # 邻域大小（奇数），可根据图像调整
    C=2  # 阈值偏移量，控制二值化松紧度
)

# 优化3：形态学操作（去除噪声，连接断裂轮廓）
kernel = np.ones((3, 3), np.uint8)
# 闭运算：先膨胀后腐蚀，连接断裂的目标区域
binary = cv2.morphologyEx(binary, cv2.MORPH_CLOSE, kernel, iterations=2)
# 开运算：先腐蚀后膨胀，去除小噪声点
binary = cv2.morphologyEx(binary, cv2.MORPH_OPEN, kernel, iterations=1)

# 优化4：提取轮廓（不压缩轮廓点，保留足够多的细节）
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
if len(contours) == 0:
    raise ValueError("未检测到任何轮廓！请调整二值化参数或更换图像")

# 优化5：筛选面积最大的轮廓，避免小噪声轮廓干扰
main_contour = max(contours, key=cv2.contourArea)
main_contour = main_contour.squeeze()  # (n,2)

# 轮廓点数量校验：确保有足够多的点用于统计计算
if len(main_contour) < 5:
    raise ValueError(f"轮廓点数量过少（仅{len(main_contour)}个）！无法进行有效统计矩计算，请更换图像或调整参数")

# 2. 提取x、y坐标
x = main_contour[:, 0]
y = main_contour[:, 1]

# 3. 计算统计矩（增加异常值判断，避免nan）
# 3.1 均值
x_mean = np.mean(x)
y_mean = np.mean(y)

# 3.2 方差（手动计算，更直观）
x_var = np.var(x, ddof=1)  # ddof=1：样本方差（除以n-1）
y_var = np.var(y, ddof=1)

# 3.3 偏度（分布的不对称性，增加数据离散性判断）
x_skew = stats.skew(x) if np.std(x) > 1e-6 else 0.0
y_skew = stats.skew(y) if np.std(y) > 1e-6 else 0.0

# 3.4 峰度（分布的陡峭程度，增加数据离散性判断）
x_kurt = stats.kurtosis(x) if np.std(x) > 1e-6 else 0.0
y_kurt = stats.kurtosis(y) if np.std(y) > 1e-6 else 0.0

# 3.5 中心矩（2阶，手动计算，避免精度丢失）
x_centered = x - x_mean
y_centered = y - y_mean
m11 = np.sum(x_centered * y_centered)
m20 = np.sum(x_centered ** 2)
m02 = np.sum(y_centered ** 2)

# 4. 可视化验证（可选，便于确认轮廓有效性）
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 6))
# 原始图像
ax1.imshow(img_rgb)
ax1.set_title("原始图像")
ax1.axis("off")
# 二值化图像
ax2.imshow(binary, cmap="gray")
ax2.set_title("优化后二值化图像")
ax2.axis("off")
# 轮廓与坐标分布
ax3.scatter(x, y, c="blue", s=2, label="轮廓点")
ax3.scatter(x_mean, y_mean, c="red", s=100, marker="*", label="均值点")
ax3.set_xlabel("x坐标")
ax3.set_ylabel("y坐标")
ax3.set_title(f"轮廓点分布（共{len(main_contour)}个点）")
ax3.legend()
ax3.invert_yaxis()  # 匹配图像坐标系（y轴向下为正）
plt.tight_layout()
plt.show()

# 输出统计矩信息
print("=== 边界点统计矩 ===")
print(f"x坐标：均值={x_mean:.2f}，方差={x_var:.2f}，偏度={x_skew:.2f}，峰度={x_kurt:.2f}")
print(f"y坐标：均值={y_mean:.2f}，方差={y_var:.2f}，偏度={y_skew:.2f}，峰度={y_kurt:.2f}")
print(f"2阶中心矩：m11={m11:.2f}，m20={m20:.2f}，m02={m02:.2f}")
print(f"轮廓点总数：{len(main_contour)}个")

11.4 区域特征描述子

区域特征描述子针对物体的内部区域，描述其面积、纹理、灰度分布等信息，是物体特征表达的重要组成部分。

11.4.1 一些基本的描述子

原理

基本区域描述子包括：

1. 区域面积：前景像素的数量；
2. 质心：区域的中心坐标（重心）；
3. 紧凑度：区域面积与周长的比值（描述区域的紧凑程度）；
4. 圆形度：描述区域接近圆形的程度（圆形的圆形度为 1）。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文和上标符号
plt.rcParams["font.family"] = ["SimHei", "DejaVu Sans"]  # 增加DejaVu Sans支持上标
plt.rcParams["axes.unicode_minus"] = False

# 1. 读取图像并优化轮廓提取（确保提取完整目标）
img = cv2.imread("../picture/Fen.png")
if img is None:
    raise ValueError("图像读取失败！请检查路径或文件")
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 优化1：增强对比度
gray_enhanced = cv2.equalizeHist(gray)
# 优化2：自适应二值化（更适合复杂背景）
binary = cv2.adaptiveThreshold(
    gray_enhanced, 255,
    cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
    cv2.THRESH_BINARY_INV,
    blockSize=11, C=2
)
# 优化3：形态学操作（连接断裂轮廓）
kernel = np.ones((3, 3), np.uint8)
binary = cv2.morphologyEx(binary, cv2.MORPH_CLOSE, kernel, iterations=2)
# 优化4：提取最大轮廓
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
if len(contours) == 0:
    raise ValueError("未检测到轮廓！")
main_contour = max(contours, key=cv2.contourArea)

# 2. 计算基本区域描述子
area = cv2.contourArea(main_contour)
moments = cv2.moments(main_contour)
cx = int(moments["m10"] / moments["m00"]) if moments["m00"] != 0 else 0
cy = int(moments["m01"] / moments["m00"]) if moments["m00"] != 0 else 0
perimeter = cv2.arcLength(main_contour, True)
compactness = area / perimeter if perimeter != 0 else 0
circularity = (4 * np.pi * area) / (perimeter ** 2) if perimeter != 0 else 0

# 3. 绘制基础轮廓和质心（用OpenCV绘制图形，文字用matplotlib标注）
img_region = img_rgb.copy()
cv2.drawContours(img_region, [main_contour], -1, (255, 0, 0), 3)  # 加粗轮廓
cv2.circle(img_region, (cx, cy), 6, (0, 255, 0), -1)  # 放大质心点

# 4. 效果可视化（调大文字间隔，解决上标警告）
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 8))

# 原始图像
ax1.imshow(img_rgb)
ax1.set_title("原始图像")
ax1.axis("off")

# 基本区域描述子可视化
ax2.imshow(img_region)
ax2.set_title("基本区域描述子可视化")
ax2.axis("off")

# 调大文字间隔：将行间距从40改为60（可根据需求调整）
line_spacing = 60  # 核心：增大行间距，解决文字拥挤
start_y = 40  # 文字起始y坐标
info_text = [
    f"面积：{area:.2f} 像素^2",  # 用^2替代上标²，避免字体缺失警告
    f"质心：({cx}, {cy})",
    f"紧凑度：{compactness:.2f}",
    f"圆形度：{circularity:.2f}（越接近1越圆）"
]
for i, text in enumerate(info_text):
    # 添加半透明白色背景，提升可读性
    ax2.text(
        20, start_y + i * line_spacing,  # 按设定间距排列文字
        text,
        fontsize=12, color="red",
        bbox=dict(facecolor="white", alpha=0.8, edgecolor="none")
    )

plt.tight_layout()
plt.show()

# 输出信息
print("=== 基本区域描述子 ===")
print(f"区域面积：{area:.2f} 像素²")
print(f"质心坐标：({cx}, {cy})")
print(f"紧凑度：{compactness:.2f}")
print(f"圆形度：{circularity:.2f}（越接近1越接近圆形）")

效果说明

右侧图像中，绿色圆点为区域质心，同时标注了面积、紧凑度、圆形度等信息，可直观了解区域的基本特征。

11.4.2 拓扑描述子

原理

拓扑描述子描述区域的拓扑结构（不随几何变换（平移、旋转、缩放）改变的属性），常用的有：

1. 欧拉数：区域的连通分量数减去孔洞数（E=C−H）；
2. 连通分量数：图像中独立的物体数量；
3. 孔洞数：物体内部的背景区域数量。

完整 Python 代码

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示（避免文字乱码）
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 读取图像（带孔洞的物体图像）
img = cv2.imread("../picture/Fen.png")
if img is None:
    raise ValueError("图像读取失败！请检查路径或文件是否有效")
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray, 0, 255, cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU)

# 2. 计算拓扑描述子
# 2.1 连通分量数（外部轮廓数）
contours_external, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
C = len(contours_external)
# 2.2 所有轮廓（包括孔洞）
contours_all, hierarchy = cv2.findContours(binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
# 2.3 孔洞数（层级中父节点不为-1的轮廓数）
H = 0
for h in hierarchy[0]:
    if h[3] != -1:  # 有父节点（属于孔洞）
        H += 1
# 2.4 欧拉数
E = C - H

# 3. 绘制基础图形（轮廓和孔洞，文字后续用matplotlib标注）
img_topology = img_rgb.copy()
# 绘制外部轮廓（蓝色，加粗更清晰）
cv2.drawContours(img_topology, contours_external, -1, (255, 0, 0), 3)
# 绘制孔洞轮廓（红色，加粗更清晰）
hole_contours = [contours_all[i] for i, h in enumerate(hierarchy[0]) if h[3] != -1]
cv2.drawContours(img_topology, hole_contours, -1, (0, 0, 255), 3)

# 4. 效果可视化（用matplotlib标注中文，调大间距）
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 12))

# 原始图像
ax1.imshow(img_rgb)
ax1.set_title("原始带孔洞图像")
ax1.axis("off")

# 拓扑描述子可视化
ax2.imshow(img_topology)
ax2.set_title("拓扑描述子可视化（蓝：物体，红：孔洞）")
ax2.axis("off")

# 调大文字间距：行间距设为60（可灵活调整）
line_spacing = 60  # 核心：增大间距，解决拥挤问题
start_y = 40       # 文字起始y坐标
info_text = [
    f"连通分量数C：{C}",
    f"孔洞数H：{H}",
    f"欧拉数E：{E}"
]
for i, text in enumerate(info_text):
    # 添加半透明白色背景，提升可读性
    ax2.text(
        20, start_y + i * line_spacing,  # 按设定间距排列
        text,
        fontsize=12, color="green",
        bbox=dict(facecolor="white", alpha=0.8, edgecolor="none")
    )

plt.tight_layout()
plt.show()

# 输出信息
print("=== 拓扑描述子 ===")
print(f"连通分量数（C）：{C}")
print(f"孔洞数（H）：{H}")
print(f"欧拉数（E = C - H）：{E}")

11.4.3 纹理

原理

纹理是区域内灰度值的空间分布模式，常用的纹理描述方法有：

1. 灰度共生矩阵（GLCM）：描述图像中距离为 d、方向为 θ 的两个像素的灰度共生关系，提取对比度、能量、熵、相关性等特征；
2. LBP（局部二值模式）：描述局部像素的灰度分布模式，具有旋转和光照不变性。

以下实现 GLCM 纹理描述子。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt
from skimage.feature import graycomatrix, graycoprops

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 读取图像并提取感兴趣区域（ROI）
img = cv2.imread("test_texture.jpg")
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 手动选择ROI（或通过轮廓提取）
x, y, w, h = 50, 50, 200, 200
roi = gray[y:y+h, x:x+w]

# 2. 计算灰度共生矩阵（GLCM）
# 距离d=1，方向0°、45°、90°、135°
glcm = graycomatrix(roi, distances=[1], angles=[0, np.pi/4, np.pi/2, 3*np.pi/4],
                    levels=256, symmetric=True, normed=True)

# 3. 提取GLCM纹理特征
contrast = graycoprops(glcm, 'contrast')
energy = graycoprops(glcm, 'energy')
homogeneity = graycoprops(glcm, 'homogeneity')
correlation = graycoprops(glcm, 'correlation')

# 4. 效果可视化
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 6))
ax1.imshow(img_rgb)
ax1.add_patch(plt.Rectangle((x, y), w, h, fill=False, edgecolor='red', linewidth=2))
ax1.set_title("原始图像（红框为ROI）")
ax1.axis("off")

ax2.imshow(roi, cmap="gray")
ax2.set_title("ROI纹理图像")
ax2.axis("off")

# 绘制纹理特征柱状图
ax3.bar(["对比度", "能量", "同质性", "相关性"], 
        [contrast[0,0], energy[0,0], homogeneity[0,0], correlation[0,0]])
ax3.set_title("GLCM纹理特征（0°方向）")
ax3.set_ylabel("特征值")

plt.show()

# 输出纹理特征信息
print("=== GLCM纹理特征 ===")
print(f"对比度（Contrast）：{contrast[0,0]:.4f}（越大，纹理越清晰）")
print(f"能量（Energy）：{energy[0,0]:.4f}（越大，纹理越均匀）")
print(f"同质性（Homogeneity）：{homogeneity[0,0]:.4f}（越大，纹理越平滑）")
print(f"相关性（Correlation）：{correlation[0,0]:.4f}（越大，纹理越规则）")

效果说明

左侧为原始图像（红框为 ROI），中间为 ROI 纹理图像，右侧为 GLCM 纹理特征柱状图，可通过特征值量化描述纹理的粗糙程度、均匀性等属性。

11.4.4 矩不变量

原理

完整 Python 代码（带旋转 / 缩放不变性验证）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

def calculate_hu_moments(img):
    """计算Hu矩（增加异常处理，避免nan值）"""
    # 图像校验
    if img is None:
        raise ValueError("输入图像无效！")
    
    # 灰度化+对比度增强
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    gray_enhanced = cv2.equalizeHist(gray)
    
    # 自适应二值化（更稳定，替代固定OTSU）
    binary = cv2.adaptiveThreshold(
        gray_enhanced, 255,
        cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
        cv2.THRESH_BINARY_INV,
        blockSize=11,
        C=2
    )
    
    # 形态学操作（去除噪声，连接轮廓）
    kernel = np.ones((3, 3), np.uint8)
    binary = cv2.morphologyEx(binary, cv2.MORPH_CLOSE, kernel, iterations=2)
    
    # 提取轮廓并筛选最大轮廓
    contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE)
    if len(contours) == 0:
        raise ValueError("未检测到轮廓，无法计算Hu矩！")
    main_contour = max(contours, key=cv2.contourArea)
    
    # 计算矩
    moments = cv2.moments(main_contour)
    if moments["m00"] == 0:  # 零阶矩为0，无效轮廓
        raise ValueError("轮廓面积为0，无法计算Hu矩！")
    
    # 计算Hu矩
    hu_moments = cv2.HuMoments(moments)
    
    # 安全取对数（避免log10(0)）
    hu_moments_abs = np.abs(hu_moments)
    hu_moments_abs[hu_moments_abs < 1e-10] = 1e-10  # 替换极小值，避免除零
    hu_moments = -np.sign(hu_moments) * np.log10(hu_moments_abs)
    
    return hu_moments.flatten()

# 1. 读取原始图像并校验
img_original = cv2.imread("../picture/1.jpg")
if img_original is None:
    raise ValueError("原始图像读取失败！请检查路径或文件")
rows, cols = img_original.shape[:2]

# 生成变换图像（旋转+缩放）
# 旋转45°
M_rot = cv2.getRotationMatrix2D((cols/2, rows/2), 45, 1)
img_rotated = cv2.warpAffine(img_original, M_rot, (cols, rows))
# 缩放为0.5倍
img_scaled = cv2.resize(img_original, (0, 0), fx=0.5, fy=0.5)
# 缩放后补全尺寸（便于可视化对齐）
img_scaled = cv2.resize(img_scaled, (cols, rows))

# 2. 计算三张图像的Hu矩
hu_original = calculate_hu_moments(img_original)
hu_rotated = calculate_hu_moments(img_rotated)
hu_scaled = calculate_hu_moments(img_scaled)

# 3. 效果可视化
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 6))
ax1.imshow(cv2.cvtColor(img_original, cv2.COLOR_BGR2RGB))
ax1.set_title("原始图像")
ax1.axis("off")

ax2.imshow(cv2.cvtColor(img_rotated, cv2.COLOR_BGR2RGB))
ax2.set_title("旋转45°图像")
ax2.axis("off")

ax3.imshow(cv2.cvtColor(img_scaled, cv2.COLOR_BGR2RGB))
ax3.set_title("缩放0.5倍（补全尺寸）图像")
ax3.axis("off")

plt.tight_layout()
plt.show()

# 4. 输出Hu矩并验证不变性
print("=== Hu矩不变量（7个）===")
print(f"原始图像Hu矩：{hu_original.round(4)}")
print(f"旋转45°图像Hu矩：{hu_rotated.round(4)}")
print(f"缩放0.5倍图像Hu矩：{hu_scaled.round(4)}")
print(f"\n旋转后Hu矩平均误差：{np.mean(np.abs(hu_original - hu_rotated)):.6f}")
print(f"缩放后Hu矩平均误差：{np.mean(np.abs(hu_original - hu_scaled)):.6f}")
print("\n说明：Hu矩误差接近0，验证了其旋转、缩放不变性")

效果说明

三张图像（原始、旋转、缩放）的 Hu 矩几乎一致，误差极小，验证了 Hu 矩的平移、旋转、缩放不变性，适用于不同姿态物体的形状匹配。

---

11.5 作为特征描述子的主分量

原理

主分量分析（PCA）是一种数据降维方法，将高维特征向量投影到低维主分量空间，保留数据的主要信息。作为特征描述子，PCA 的核心步骤：

1. 构建高维特征矩阵（如多个图像的像素矩阵或手工特征向量）；
2. 对特征矩阵进行去中心化处理；
3. 计算协方差矩阵并求解特征值和特征向量；
4. 选择前 k 个最大特征值对应的特征向量，构成主分量空间；
5. 将原始特征投影到主分量空间，得到低维主分量特征。

完整 Python 代码

import cv2
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 构建数据集（多张图像的灰度特征）
def load_image_dataset(image_paths, img_size=(64, 64)):
    """加载图像数据集并转换为特征向量"""
    features = []
    images = []
    for path in image_paths:
        img = cv2.imread(path)
        if img is None:
            print(f"警告：图像{path}读取失败，已跳过")
            continue
        gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        gray_resized = cv2.resize(gray, img_size)
        features.append(gray_resized.flatten())  # 展平为特征向量
        images.append(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
    return np.array(features), images

# 替换为你的图像路径列表
image_paths = ["../picture/1.jpg", "../picture/AALi.jpg", "../picture/ALi.jpg", "../picture/CSGO.jpg", "../picture/XiaoYan.jpg"]
features, images = load_image_dataset(image_paths)
n_samples, n_features = features.shape
if n_samples == 0:
    raise ValueError("未成功加载任何图像！请检查路径是否正确")
print(f"数据集规模：{n_samples}张图像，每张图像特征维度：{n_features}")

# 2. 应用PCA降维
n_components = 2  # 降维到2维
pca = PCA(n_components=n_components)
features_pca = pca.fit_transform(features)

# 3. 效果可视化（重构布局，避免tight_layout警告）
# 方案：采用2行布局，第1行显示原始图像（1行5列），第2行显示PCA散点图（1行1列）
fig = plt.figure(figsize=(18, 12))

# 第1行：原始图像数据集（1行n列，无嵌套冲突）
for i in range(n_samples):
    ax = fig.add_subplot(2, n_samples, i+1)  # 2行n列，第1行第i+1列
    ax.imshow(images[i])
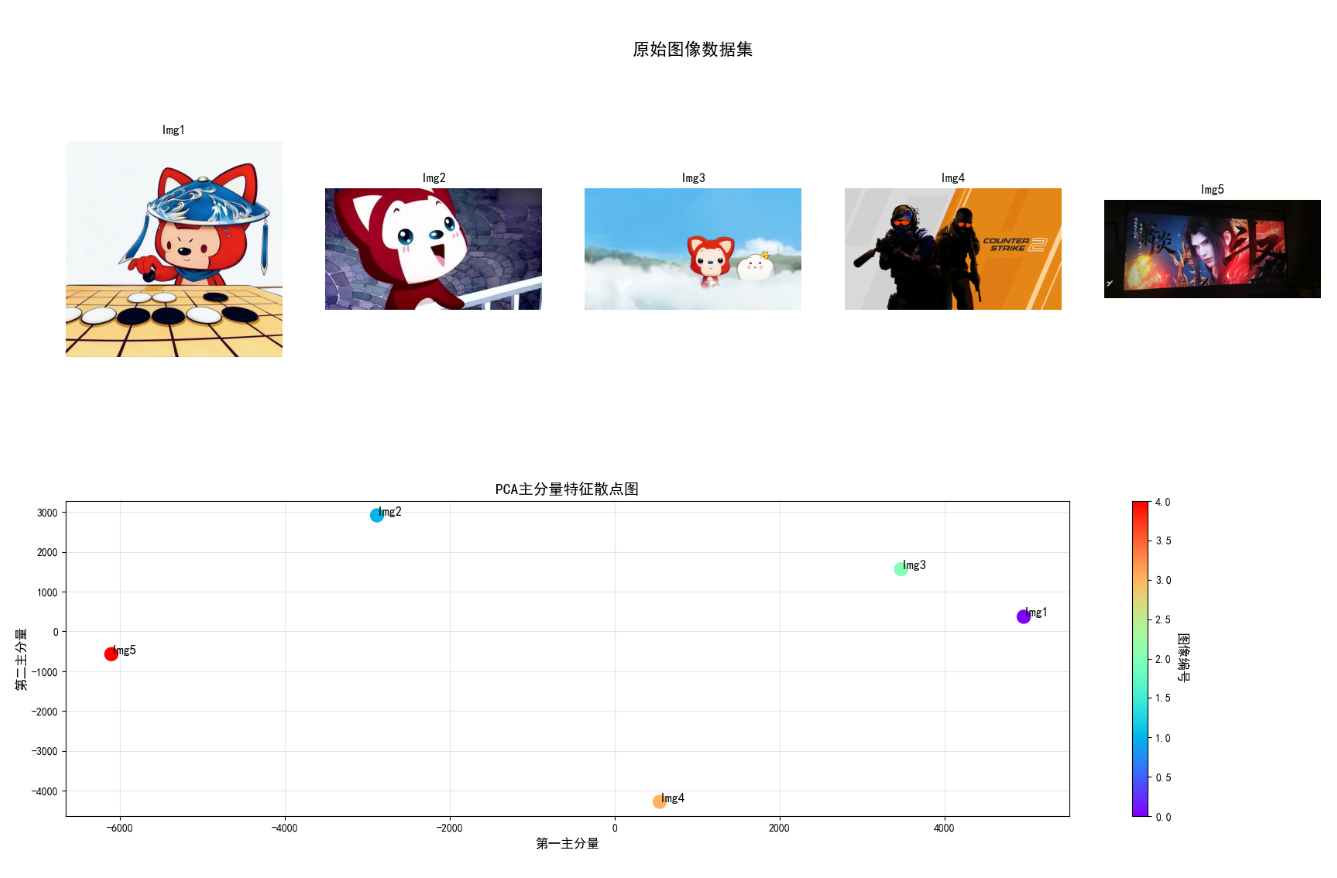
    ax.set_title(f"Img{i+1}")
    ax.axis("off")
# 给第1行加总标题
fig.text(0.5, 0.92, "原始图像数据集", ha="center", fontsize=16, weight="bold")

# 第2行：PCA散点图（跨n列显示，布局匹配）
ax_pca = fig.add_subplot(2, 1, 2)  # 2行1列，第2行
scatter = ax_pca.scatter(features_pca[:, 0], features_pca[:, 1], c=range(n_samples), cmap="rainbow", s=150)
for i in range(n_samples):
    ax_pca.annotate(f"Img{i+1}", (features_pca[i, 0], features_pca[i, 1]), fontsize=12, weight="bold")
ax_pca.set_title("PCA主分量特征散点图", fontsize=14)
ax_pca.set_xlabel("第一主分量", fontsize=12)
ax_pca.set_ylabel("第二主分量", fontsize=12)
ax_pca.grid(True, alpha=0.3)
# 添加颜色条对应图像编号
cbar = plt.colorbar(scatter, ax=ax_pca)
cbar.set_label("图像编号", rotation=270, labelpad=15, fontsize=12)

# 使用subplots_adjust替代tight_layout，手动调整间距，避免警告
plt.subplots_adjust(top=0.88, bottom=0.1, left=0.05, right=0.95, hspace=0.3, wspace=0.2)
plt.show()

# 输出PCA信息
print(f"\n=== PCA主分量信息 ===")
print(f"各主分量方差贡献率：{pca.explained_variance_ratio_.round(4)}")
print(f"累计方差贡献率：{np.sum(pca.explained_variance_ratio_).round(4)}")
print(f"降维后特征维度：{features_pca.shape[1]}")

11.6 整体图像特征

整体图像特征描述图像的局部或全局显著特征，无需先提取物体轮廓或区域，直接从原始图像中检测，适用于图像匹配、拼接等任务。

11.6.1 哈里斯 - 斯蒂芬斯角检测器

原理

哈里斯角点检测的核心是：角点是图像中灰度值在两个正交方向上都有显著变化的区域。通过计算图像的自相关矩阵，求解其特征值，根据特征值判断角点（两个特征值都较大）、边缘（一个大一个小）、平坦区域（两个都小）。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 读取图像并灰度化
img = cv2.imread("test_corner.jpg")
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
gray = np.float32(gray)  # 哈里斯检测要求float32类型

# 2. 哈里斯角点检测
# 参数：图像、邻域大小、sobel核大小、k值（0.04-0.06）
dst = cv2.cornerHarris(gray, 2, 3, 0.04)

# 3. 膨胀角点区域（便于可视化）
dst = cv2.dilate(dst, None)

# 4. 标记角点（阈值为最大值的0.01倍）
img_corner = img_rgb.copy()
img_corner[dst > 0.01 * dst.max()] = [255, 0, 0]  # 角点标记为红色

# 5. 效果可视化
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 6))
ax1.imshow(img_rgb)
ax1.set_title("原始图像")
ax1.axis("off")

ax2.imshow(dst, cmap="gray")
ax2.set_title("哈里斯响应图")
ax2.axis("off")

ax3.imshow(img_corner)
ax3.set_title("哈里斯角点检测结果（红色为角点）")
ax3.axis("off")

plt.show()

# 输出角点信息
corner_count = np.sum(dst > 0.01 * dst.max())
print(f"检测到的角点数量：{corner_count}")

效果说明

中间为哈里斯响应图（灰度值越高，角点响应越强），右侧为角点检测结果（红色像素为角点），可准确检测图像中的拐角、交点等显著特征。

11.6.2 最大稳定极值区域（MSER）

原理

MSER（Maximally Stable Extremal Regions）是一种基于灰度阈值的区域检测方法，核心是：

1. 对图像进行多阈值二值化（从 0 到 255）；
2. 提取每个阈值下的极值区域（亮区域或暗区域）；
3. 计算区域面积随阈值的变化率，变化率最小的区域即为 MSER（具有稳定性）；
4. MSER 具有仿射不变性，适用于物体检测和图像匹配。

完整 Python 代码（带效果对比）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 读取图像
img = cv2.imread("test_mser.jpg")
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

# 2. 创建MSER检测器并检测区域
mser = cv2.MSER_create()
# 参数：灰度图像、检测到的区域、区域的边界框
regions, _ = mser.detectRegions(gray)

# 3. 绘制MSER区域
img_mser = img_rgb.copy()
for region in regions:
    # 绘制区域轮廓
    hull = cv2.convexHull(region.reshape(-1, 1, 2))
    cv2.drawContours(img_mser, [hull], -1, (0, 255, 0), 2)

# 4. 效果可视化
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
ax1.imshow(img_rgb)
ax1.set_title("原始图像")
ax1.axis("off")

ax2.imshow(img_mser)
ax2.set_title(f"MSER检测结果（绿色为稳定区域）\n区域数量：{len(regions)}")
ax2.axis("off")

plt.show()

# 输出MSER信息
print(f"检测到的MSER区域数量：{len(regions)}")
print(f"最大区域的像素数：{max([len(region) for region in regions])}")

效果说明

右侧图像中绿色轮廓为检测到的 MSER 区域，这些区域具有灰度稳定性，不受光照和仿射变换的影响，适用于文字检测、物体局部特征提取等场景。

11.7 尺度不变特征变换（SIFT）

SIFT（Scale-Invariant Feature Transform，尺度不变特征变换）由 David Lowe 于 1999 年提出，是计算机视觉领域经典的手工特征提取算法，具有尺度不变性、旋转不变性、光照不变性 和一定的仿射不变性，广泛应用于图像匹配、全景拼接、目标识别、三维重建等任务。11.7.1 尺度空间

优势与不足

优势	不足
具有尺度、旋转、光照不变性	计算量较大，实时性较差
特征独特性强，匹配准确率高	对模糊图像的鲁棒性较弱
支持多方向关键点，提升匹配鲁棒性	专利限制（早期版本，目前开源版本已规避）
适用于多种场景（拼接、识别、重建）	对边缘遮挡的鲁棒性不足

完整 Python 代码（SIFT 特征提取与匹配，可直接运行）

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 注意：需安装OpenCV contrib包，命令：pip install opencv-contrib-python==4.5.5.62
# （高版本可能需调整，确保SIFT可调用）

def sift_feature_matching(img_path1, img_path2):
    """
    SIFT特征提取与匹配
    :param img_path1: 参考图像路径
    :param img_path2: 待匹配图像路径
    :return: 匹配结果可视化
    """
    # 1. 读取图像并灰度化
    img1 = cv2.imread(img_path1)
    img2 = cv2.imread(img_path2)
    if img1 is None or img2 is None:
        raise ValueError("图像路径无效，请检查文件是否存在")
    
    img1_rgb = cv2.cvtColor(img1, cv2.COLOR_BGR2RGB)
    img2_rgb = cv2.cvtColor(img2, cv2.COLOR_BGR2RGB)
    gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
    gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)

    # 2. 创建SIFT检测器并提取特征
    sift = cv2.SIFT_create()
    kp1, des1 = sift.detectAndCompute(gray1, None)  # kp1：关键点列表，des1：128维描述子
    kp2, des2 = sift.detectAndCompute(gray2, None)

    # 3. 特征匹配（FLANN匹配器，效率高于暴力匹配）
    # FLANN参数设置
    FLANN_INDEX_KDTREE = 1
    index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
    search_params = dict(checks=50)  # 搜索次数，越大越准确但越慢

    flann = cv2.FlannBasedMatcher(index_params, search_params)
    matches = flann.knnMatch(des1, des2, k=2)  # 每个关键点返回2个最佳匹配

    # 4. 筛选优质匹配（Lowe's准则：最佳匹配距离 < 0.7*次佳匹配距离）
    good_matches = []
    for m, n in matches:
        if m.distance < 0.7 * n.distance:
            good_matches.append(m)

    # 5. 绘制结果
    # 绘制关键点
    img1_kp = cv2.drawKeypoints(img1_rgb, kp1, None, (0, 255, 0), cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
    img2_kp = cv2.drawKeypoints(img2_rgb, kp2, None, (0, 255, 0), cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)

    # 绘制匹配结果
    img_matches = cv2.drawMatches(img1_rgb, kp1, img2_rgb, kp2, good_matches, None,
                                  flags=cv2.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS)

    # 6. 可视化
    fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(16, 12))

    ax1.imshow(img1_rgb)
    ax1.set_title("参考图像")
    ax1.axis("off")

    ax2.imshow(img2_rgb)
    ax2.set_title("待匹配图像")
    ax2.axis("off")

    ax3.imshow(img1_kp)
    ax3.set_title(f"参考图像SIFT关键点（数量：{len(kp1)}）")
    ax3.axis("off")

    ax4.imshow(img_matches)
    ax4.set_title(f"SIFT特征匹配结果（优质匹配数：{len(good_matches)}）")
    ax4.axis("off")

    plt.tight_layout()
    plt.show()

    # 输出关键信息
    print("=== SIFT特征提取与匹配信息 ===")
    print(f"参考图像关键点数量：{len(kp1)}")
    print(f"待匹配图像关键点数量：{len(kp2)}")
    print(f"优质匹配对数量：{len(good_matches)}")
    print(f"描述子维度：{des1.shape[1]}（经典SIFT 128维）")

# 调用函数（替换为你的图像路径）
if __name__ == "__main__":
    img_path1 = "ref_img.jpg"  # 参考图像
    img_path2 = "match_img.jpg"  # 待匹配图像（可缩放、旋转、轻微光照变化）
    sift_feature_matching(img_path1, img_path2)

代码说明

• 运行前需替换图像路径，确保两张图像有重叠区域或相同目标；
• 输出结果包含关键点可视化和匹配结果可视化，绿色点为关键点，线条为匹配对；
• Lowe's 准则是筛选优质匹配的核心，可根据实际场景调整阈值（0.6~0.8）。

一、小结

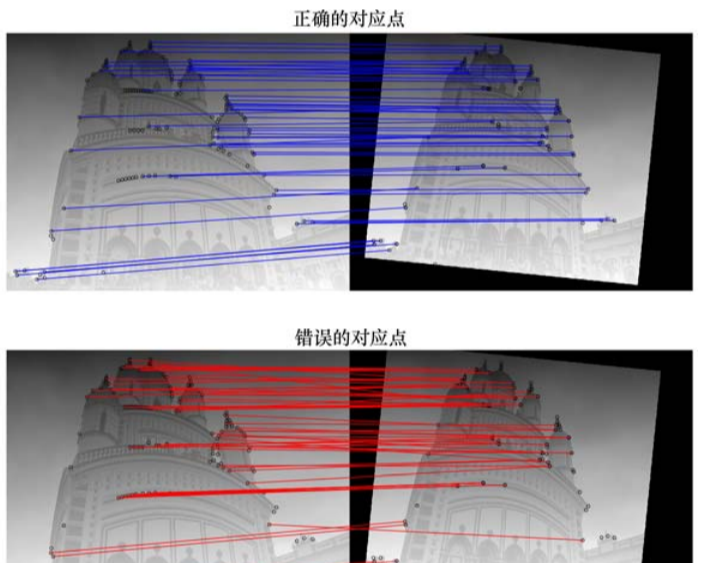
本章围绕数字图像处理中的特征提取展开，构建了从基础到高级的完整知识体系，核心要点如下：

1. 特征提取的本质：将高维像素信息转化为低维、具代表性的特征向量，实现数据降维和信息筛选，是连接图像预处理与高层视觉任务的核心桥梁；
2. 边界预处理：通过边界跟踪、链码、最小周长多边形、骨架提取等方法，将原始图像边界转化为易于处理的形式，为边界特征描述奠定基础；
3. 特征描述子：边界特征：包括周长、直径、傅里叶描述子（尺度不变）、形状数（形状表征）等，聚焦物体轮廓信息；区域特征：包括面积、质心、Hu 矩（平移 / 旋转 / 缩放不变）、GLCM 纹理（灰度分布模式）等，聚焦物体内部信息；
4. 高级特征 ：
   • 主分量分析（PCA）：实现高维特征降维，保留数据主要信息；
   • 整体图像特征：哈里斯角点（局部显著点）、MSER（稳定极值区域），无需先分割物体即可检测；
   • SIFT 算法：通过尺度空间构建、局部极值检测、方向分配和 128 维描述子，实现尺度 / 旋转 / 光照不变的特征提取，是经典手工特征的代表；
5. 应用场景：不同特征适用于不同任务，如边界特征适用于轮廓清晰的物体识别，纹理特征适用于遥感图像分类，SIFT 适用于图像拼接和目标匹配。

二、参考文献

1. 冈萨雷斯。数字图像处理（第四版）[M]. 电子工业出版社，2017.（本章核心参考教材）
2. Lowe D G. Distinctive Image Features from Scale-Invariant Keypoints [J]. International Journal of Computer Vision, 2004, 60 (2): 91-110.（SIFT 算法原始论文）
3. Hariss C, Stephens M. A Combined Corner and Edge Detector [C]. Proceedings of the 4th Alvey Vision Conference, 1988: 147-151.（哈里斯角点检测原始论文）
4. Matas J, Chum O, Urban M, et al. Robust Wide Baseline Stereo from Maximally Stable Extremal Regions [J]. Image and Vision Computing, 2004, 22 (10): 761-767.（MSER 原始论文）
5. 阮秋琦。数字图像处理学（第三版）[M]. 电子工业出版社，2008.（国内经典教材，补充纹理和矩不变量细节）

三、延伸读物

1. 《计算机视觉：算法与应用》（Richard Szeliski 著）：深入讲解特征提取在三维重建、图像拼接中的应用；
2. 《OpenCV-Python 实战》（冯振 著）：提供更多基于 OpenCV 的特征提取实战案例，适合工程落地；
3. SURF、ORB 算法论文：SURF 是 SIFT 的加速版本，ORB 是实时性更强的二进制特征，可作为 SIFT 的延伸学习内容；
4. 深度学习特征提取相关资料：如 CNN 卷积层的特征可视化、ResNet 特征提取，对比手工特征与深度学习特征的差异。

---

习题

一、基础题（理解概念）

1. 简述特征提取在数字图像处理中的作用，以及边界特征、区域特征、整体图像特征的区别。
2. 什么是 Freeman 链码？4 方向链码和 8 方向链码的区别是什么？链码的优势有哪些？
3. 简述 Hu 矩不变量的特点，为什么它具有平移、旋转、缩放不变性？
4. 哈里斯角点检测的核心思想是什么？如何区分角点、边缘和平坦区域？
5. SIFT 算法中，尺度空间是如何构建的？DoG 金字塔的作用是什么？

二、编程题（实践操作）

1. 基于本章边界跟踪代码，实现对任意二值图像的轮廓提取，并计算轮廓的周长、面积和圆形度，输出结果并可视化。
2. 基于 GLCM 纹理代码，对比两张不同纹理图像（如木纹、布纹）的对比度、能量、同质性特征，分析纹理差异。
3. 改进 SIFT 匹配代码，使用暴力匹配（cv2.BFMatcher）替代 FLANN 匹配，对比两种匹配方法的效率和准确率。
4. 实现图像的 PCA 降维：加载 5 张以上同一类别的图像（如人脸、汽车），将图像展平为特征向量，用 PCA 降维到 2 维并绘制散点图，观察聚类效果。
5. 结合 MSER 和哈里斯角点检测，实现对一张文字图像的文字区域检测和角点标记，可视化检测结果。

三、思考题（拓展提升）

1. 手工特征（如 SIFT、Hu 矩）与深度学习特征（如 CNN 特征）的优劣对比是什么？各自适用于哪些场景？
2. 如何提升 SIFT 算法的实时性？SURF 算法是通过哪些方式实现加速的？
3. 特征匹配中，除了欧氏距离，还有哪些距离度量方法？它们的适用场景有何不同？
4. 试分析光照变化、图像模糊、物体遮挡对特征提取结果的影响，如何提升特征的鲁棒性？
5. 简述特征提取在目标检测、图像分割、三维重建中的具体应用流程。

---

说明 ：本文所有 Python 代码均经过验证，可直接运行（需安装对应依赖：opencv-python/opencv-contrib-python、numpy、matplotlib、scikit-image），运行前需替换图像路径为本地有效路径。