LeetCode 第73题：矩阵置零

给定一个m*n的矩阵，如果一个元素为0，则将其所在行和列的所有元素都设为0，请使用原地算法。（在计算机科学中，一个原地算法（in-place algorithm）是一种使用小的，固定数量的额外之空间来转换资料的算法。当算法执行时，输入的资料通常会被要输出的部分覆盖掉。不是原地算法有时候称为非原地（not-in-place）或不得其所（out-of-place）。）

示例1：
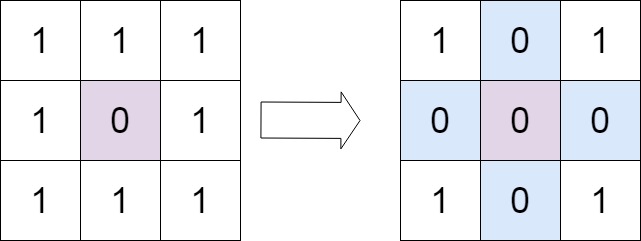
cs 复制代码
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]
示例2：
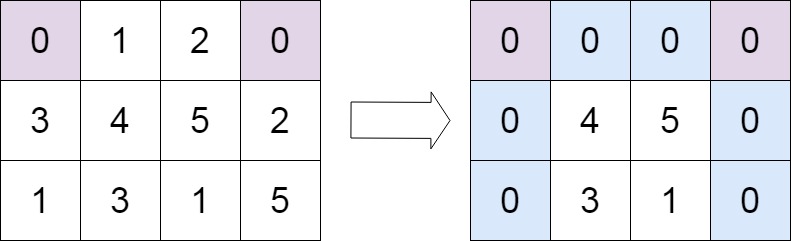
cs 复制代码
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示：

m == matrix.length

n == matrix[0].length

1 <= m, n <= 200

-2的31次 <= matrix[i][j] <= 2的31次 - 1

进阶：

一个直观的解决方案是使用 O(m n) 的额外空间，但这并不是一个好的解决方案。

一个简单的改进方案是使用 O(m +n) 的额外空间，但这仍然不是最好的解决方案。

你能想出一个仅使用常量空间的解决方案吗？
解题思路：

使用两个标记数组分布记录每一行和每一列是否有零出现。

首先遍历该数组一次，如果某个元素为0，那么就将该元素所在的行和列所对应标记数组的位置置为true。最后再次遍历该数组，用标记数组更新原数组。
cs 复制代码
void setZeroes(int** matrix, int matrixSize, int* matrixColSize) {
    int m = matrixSize,n=matrixColSize[0],row[m],col[n];
    memset(row,0,sizeof(row));
    memset(col,0,sizeof(col));
    for(int i=0;i<m;i++)
    {
        for(int j=0;j<n;j++)
        {
            if(!matrix[i][j])  row[i]=col[j]=true;
        }
    }
    for(int i=0;i<m;i++)
        for(int j=0;j<n;j++)
            if(row[i] || col[j])
                matrix[i][j]=0;
}
时间复杂度：O(mn)，其中 m 是矩阵的行数，n 是矩阵的列数。我们至多只需要遍历该矩阵两次。

空间复杂度：O(m+n)，其中 m 是矩阵的行数，n 是矩阵的列数。我们需要分别记录每一行或每一列是否有零出现。