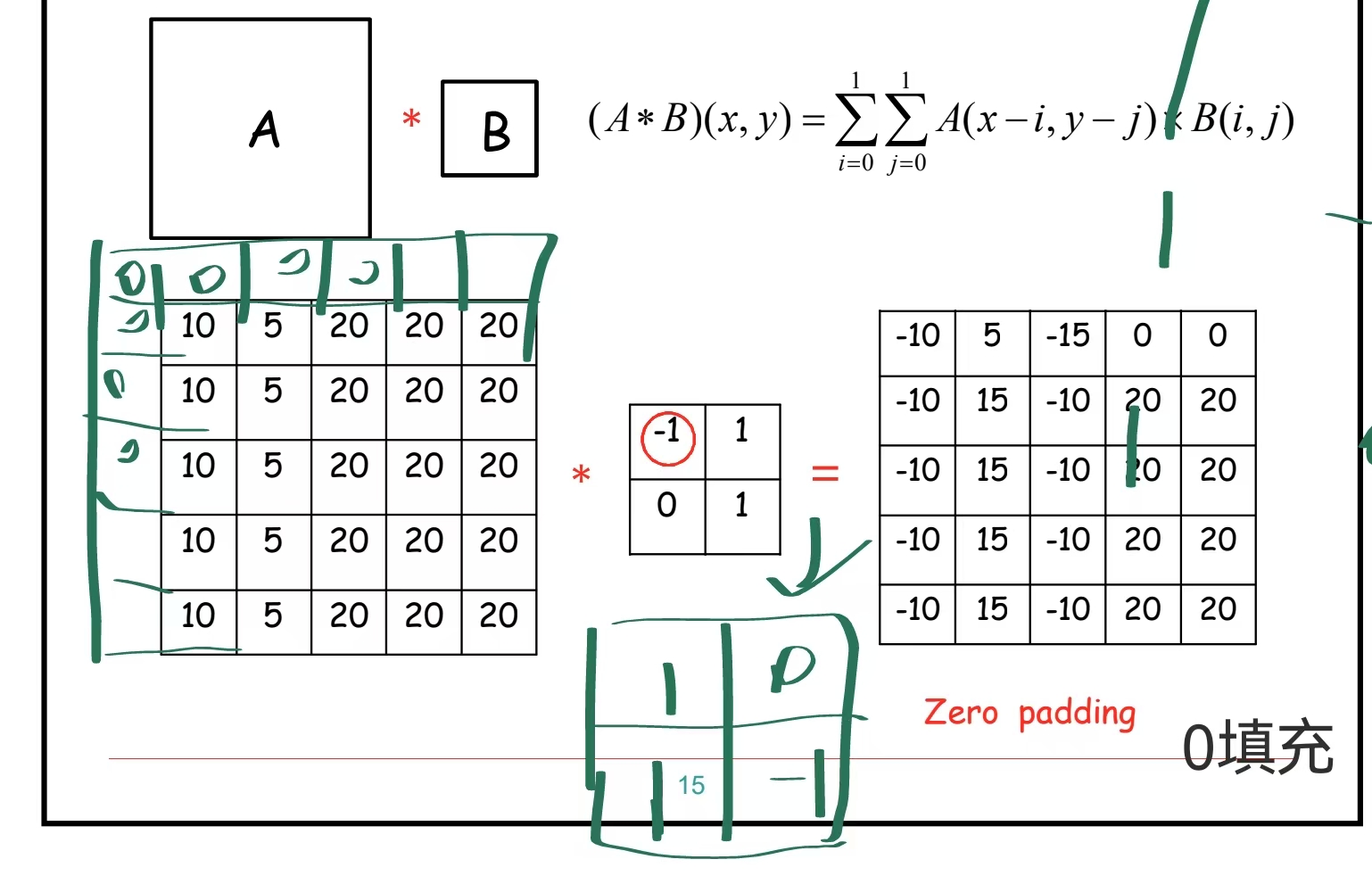
我们要计算两个矩阵的卷积。卷积操作在图像处理、信号处理等领域很常见。这里我们以二维离散卷积为例。
卷积操作的基本步骤:
- 将卷积核翻转180度(即旋转180度,也可以先沿x轴翻转再沿y轴翻转)。
- 将翻转后的卷积核覆盖在输入矩阵上,从左上角开始,每次移动一个位置。
- 在每个位置上,将卷积核与输入矩阵对应元素相乘,然后将乘积求和,得到输出矩阵在该位置的值。
- 重复步骤2和3,直到覆盖整个输入矩阵。
注意:边界处理通常有几种方式,比如忽略边界(输出尺寸变小)、补零等。这里我们默认使用"valid"模式,即只在卷积核完全覆盖输入矩阵的位置计算,输出尺寸会变小;如果需要全尺寸输出,则需要在输入矩阵周围补零("same"模式)。
但实际计算时,我们通常使用更简便的方法:直接滑动相乘相加,而不显式翻转,因为离散卷积中翻转180度后的卷积核滑动相乘就相当于翻转后的点积。但注意,如果按照严格的数学定义,是需要翻转的。不过在图像处理中,我们通常使用对称的卷积核(如高斯核),翻转后不变,所以可以忽略翻转步骤。
但是,为了严谨起见,我们还是按照数学定义进行:先翻转卷积核,然后再滑动点积。
例:计算矩阵A和卷积核K的卷积
设矩阵A为:
A = [[1, 2, 3],
4, 5, 6\], \[7, 8, 9\]
卷积核K为:
K = [[1, 0],
0, -1\]
注意:在卷积操作中,卷积核是要翻转的,所以先翻转K(旋转180度)得到:
K_rotated = [[-1, 0],
0, 1\]
现在,我们将翻转后的卷积核在矩阵A上滑动。按照valid模式(即卷积核完全覆盖在A上时),输出矩阵的大小为 (3-2+1) x (3-2+1) = 2x2。
具体计算:
第一步:覆盖A的左上角2x2区域:
1,2
4,5
与翻转后的卷积核(K_rotated)对应位置相乘并求和:
(1 * (-1) + 2 * 0 + 4 * 0 + 5 * 1) = (-1) + 0 + 0 + 5 = 4
第二步:向右移动一个位置,覆盖区域:
2,3
5,6
计算: (2 * (-1) + 3 * 0 + 5 * 0 + 6 * 1) = -2 + 0 + 0 + 6 = 4
第三步:向下移动一个位置,覆盖区域:
4,5
7,8
计算: (4 * (-1) + 5 * 0 + 7 * 0 + 8 * 1) = -4 + 0 + 0 + 8 = 4
第四步:再向右移动,覆盖区域:
5,6
8,9
计算: (5 * (-1) + 6 * 0 + 8 * 0 + 9 * 1) = -5 + 0 + 0 + 9 = 4
因此,输出矩阵为:
\[4, 4\], \[4, 4\]\]。 求矩阵A与矩阵B的卷积,先将B沿X轴翻转,然后沿Y轴翻转,然后将矩阵A左边一列和上边一列补0,然后对应位相乘并相加,得到某一位的结果。