一、引言
高性能计算(HPC)是科学研究和工程应用的重要支撑,而矩阵运算是 HPC 领域最基础也最重要的操作之一。本文将通过一个简单但实用的案例,矩阵乘法的并行优化,从零开始在鲲鹏平台上进行 HPC 开发实践。
二、环境准备
1.硬件与系统要求
- 硬件: 鲲鹏 920 处理器(或其他鲲鹏系列)
- 操作系统: openEuler 20.03 LTS 或 CentOS 7.6+
- 内存: 建议 8GB 以上
2.基于Visual Studio Code安装鲲鹏
基于 Visual Studio Code 为开发者提供面向鲲鹏平台进行应用软件开发、迁移、性能加速、编译调试、性能调优、亲和分析等一系列端到端工具,即插即用。
我们可以直接在Visual Studio Code的插件中去搜索下载:
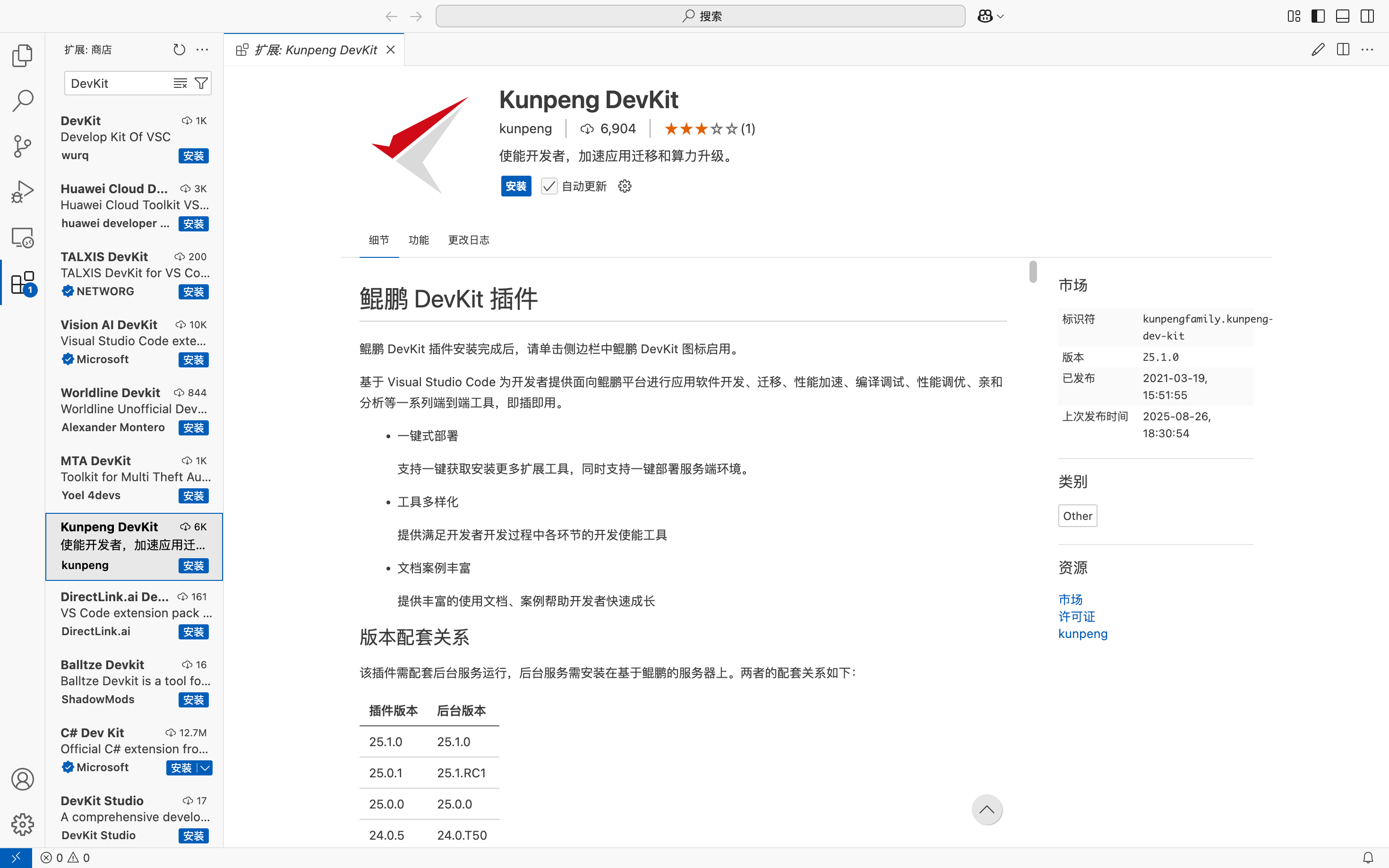
安装完成之后我们会看到如下界面:
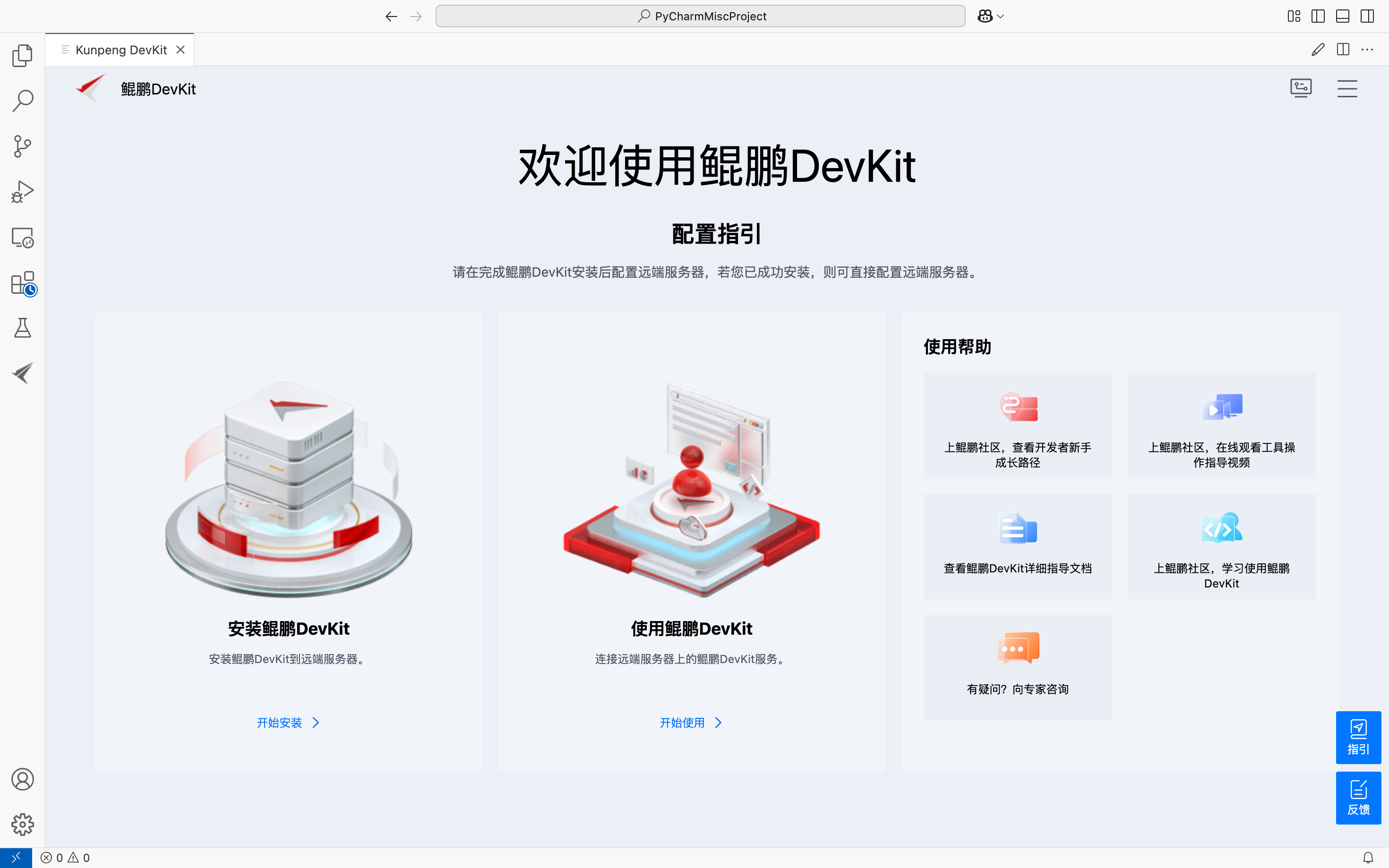
3.服务器检测
这里需要我们输入自己的服务器地址还有端口号以及密码,待部署工具的服务器SSH端口,默认为22。登录待部署工具的服务器操作系统的用户名,默认为root用户,然后输入待部署工具的服务器操作系统的密码:
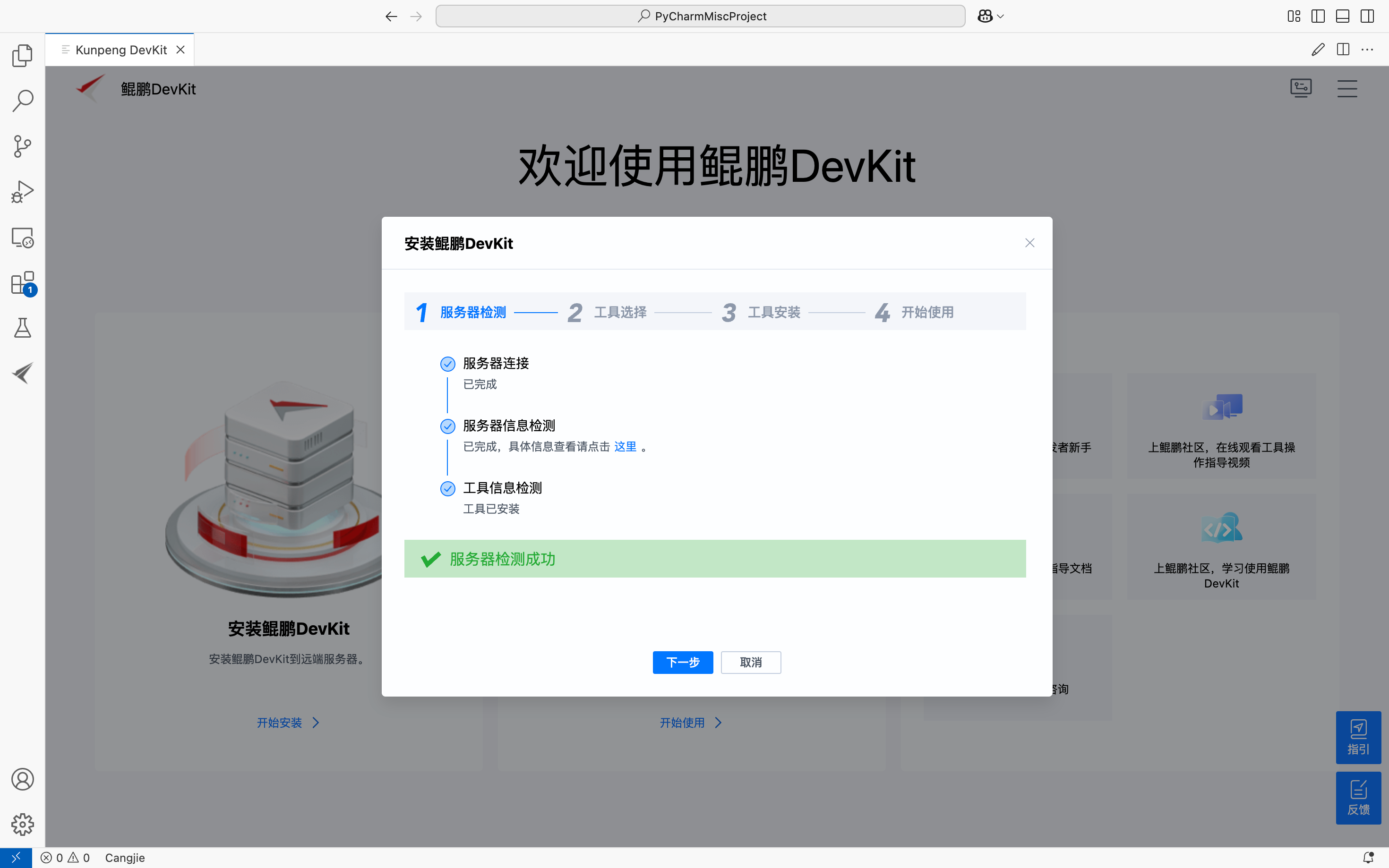
4.工具选择
安装方式分为以下两种:
- 在线安装:远程服务器与外部网络连接,在线自动获取弹性框架和已选择的工具软件包并完成安装。
可以选择在线安装,如下所示:
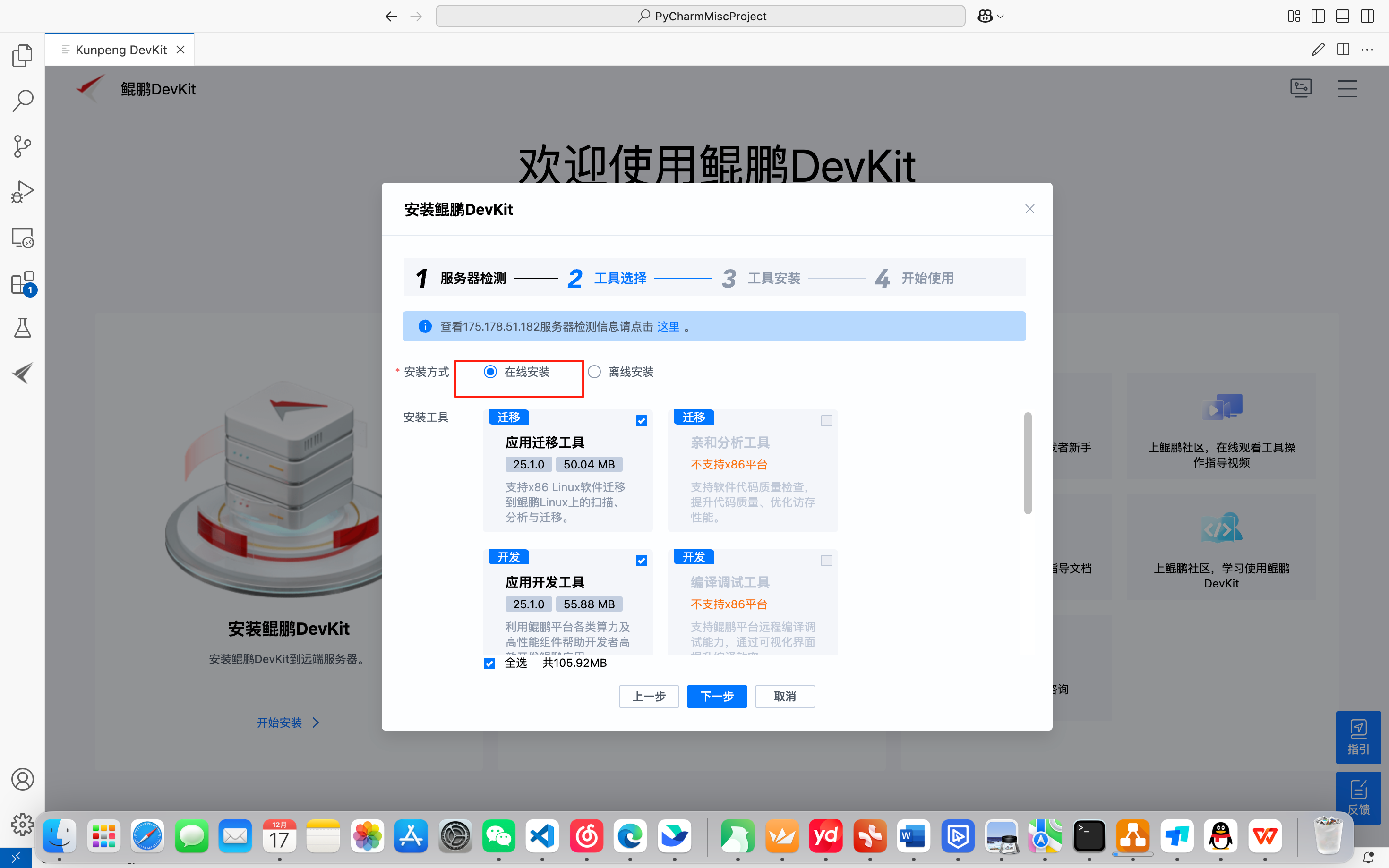
- 离线安装:远程服务器与外部网络隔离,需手动上传弹性框架安装包。
也可以选择离线安装,需要我们在本地下载好安装包,然后点击上传:
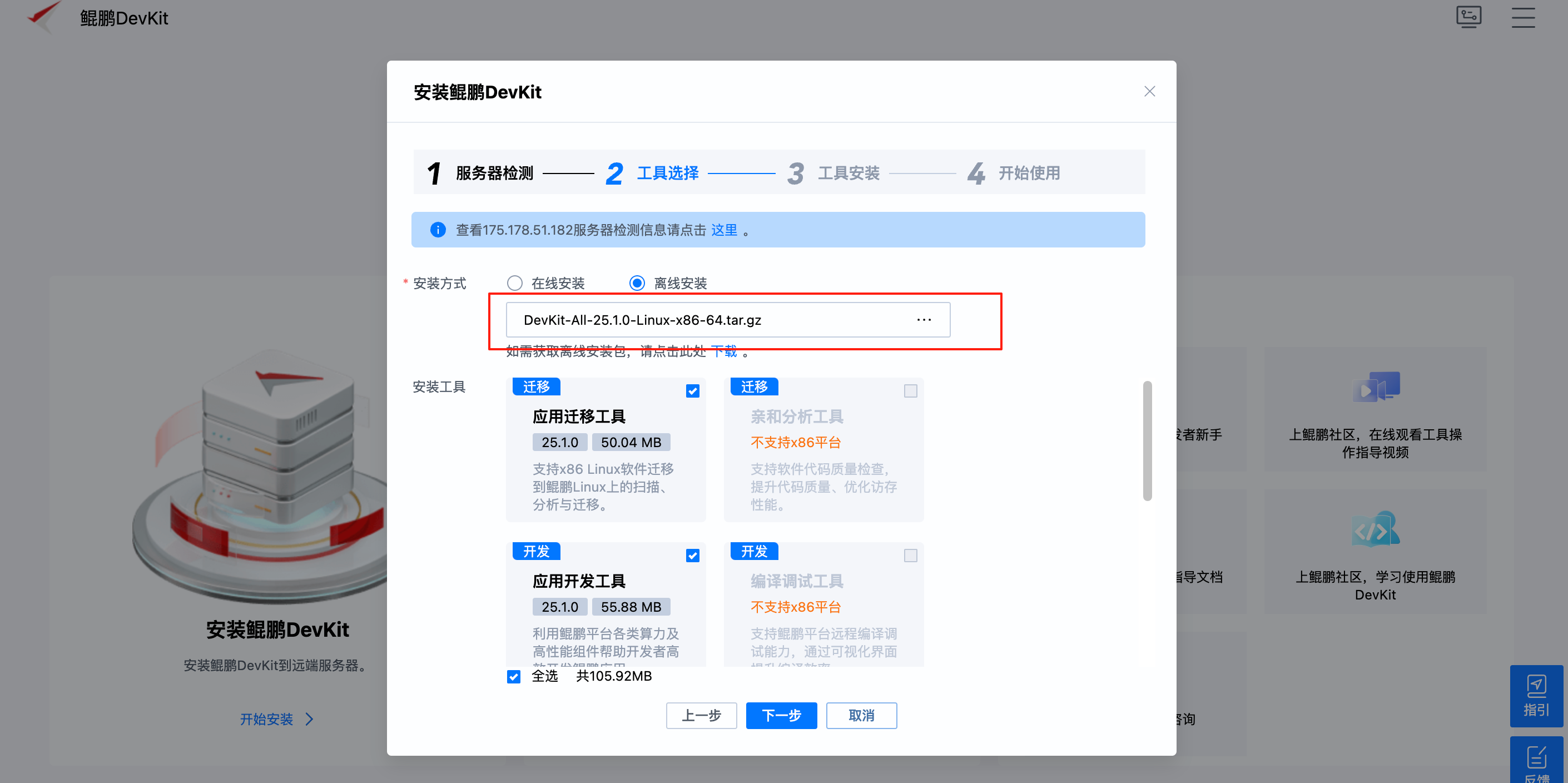
5.工具安装
这里首先会提示当前操作系统版本不在鲲鹏 DevKit 官方支持的兼容列表中,强行安装 / 运行可能导致失败(如功能异常、无法启动等);接下来需要你手动选择当前系统所属的 OS 系列,确认后继续安装,或输入<font style="background-color:rgb(187,191,196);">no</font>退出。这里一定要选择自己合适的,选择1或2或3:

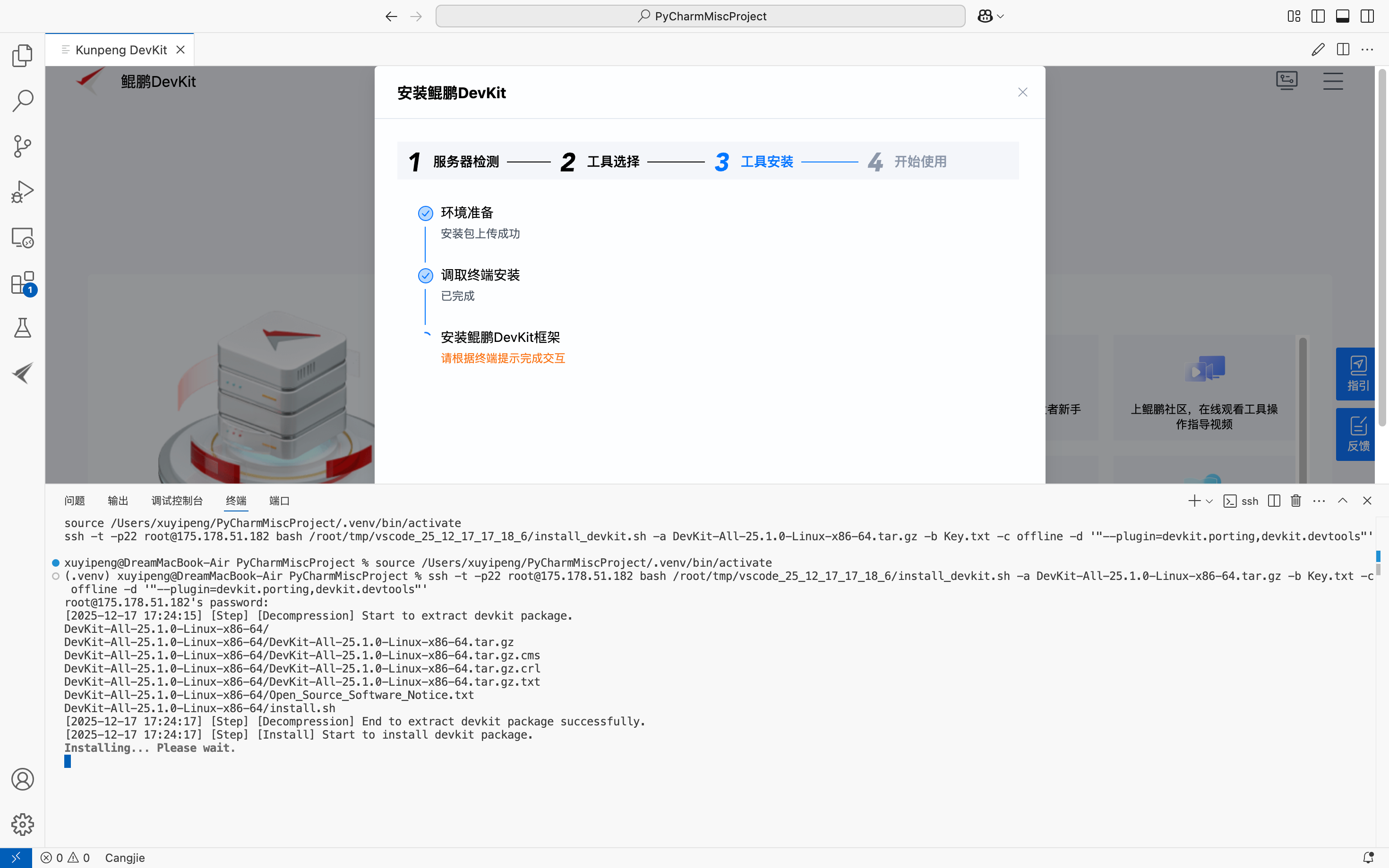
后面根据指令一路同意下去即可:
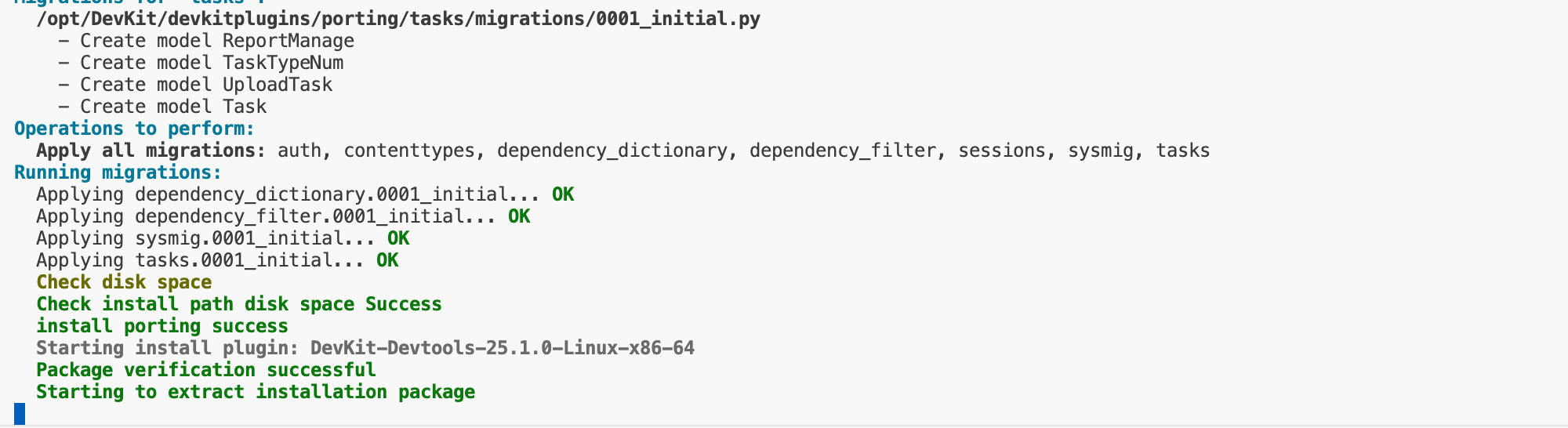
最后就会出现已经安装好的截图:
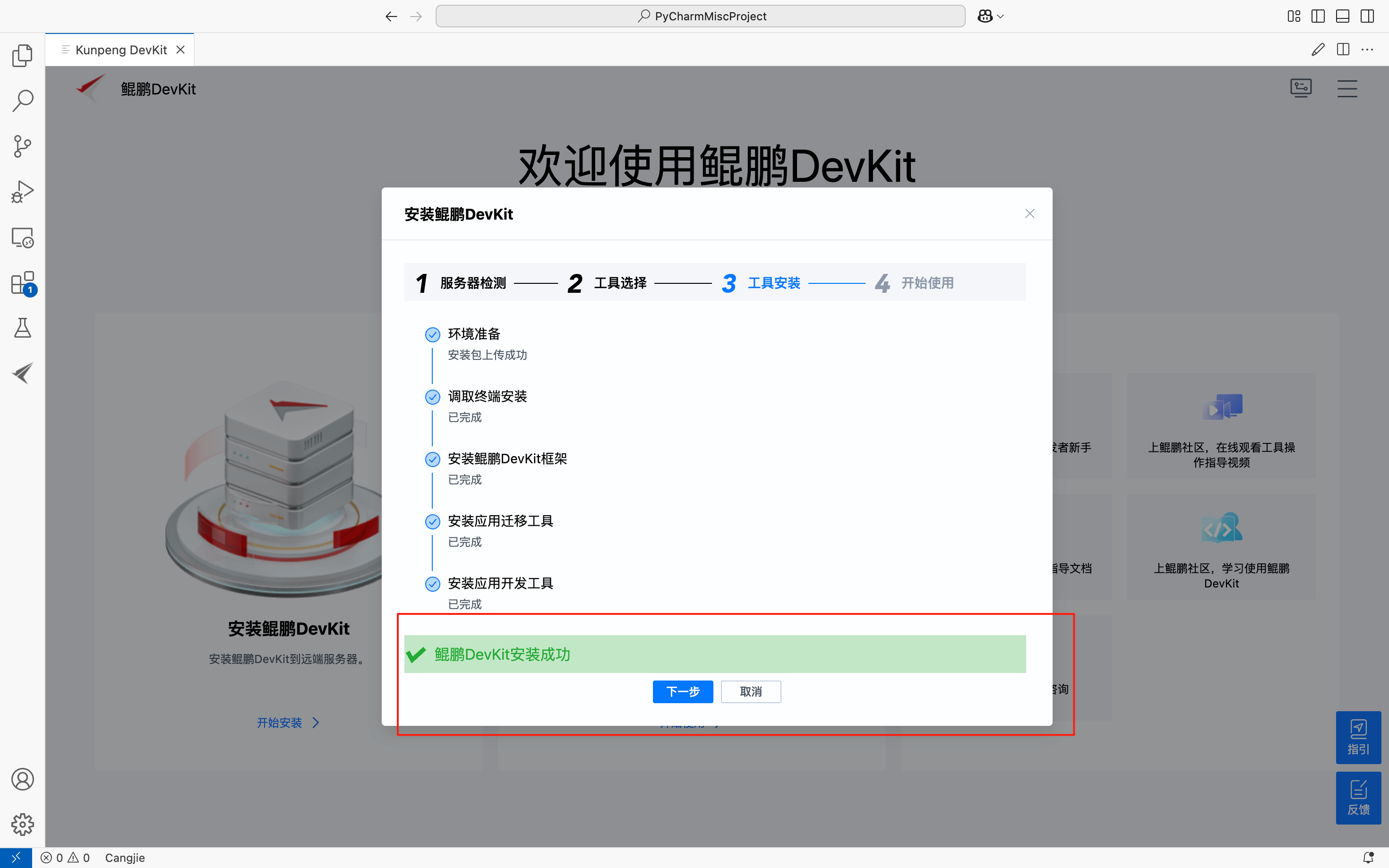
6.开始使用
工具部署完成后,单击立即登录,输入用户名和密码,用户名是登录工具的用户,默认的管理员为devadmin,工具部署完成后首次登录需要创建管理员密码。单击"登录",登录时需阅读"使用声明"并勾选"我已阅读并同意",单击"确定"进入鲲鹏DevKit插件主界面。
具部署完成后,单击右上角,在下拉菜单中选择"配置远端服务器"可切换到其他已经部署了鲲鹏DevKit的服务器:

7.安装开发工具
plain
# 更新系统
sudo yum update -y
# 安装基础开发工具
sudo yum install gcc gcc-c++ make -y
# 安装鲲鹏优化编译器(可选,推荐)
# 下载地址:https://www.hikunpeng.com/developer/devkit/compiler
# 或使用系统自带 GCC 8.3+
# 验证安装
gcc --version三、实践案例:矩阵乘法的简单优化
我们以 1024×1024 双精度(double)矩阵乘法为载体,从基准版本出发,通过缓存优化逐步释放鲲鹏平台算力,在后面的文章中我们扩展多线程、矢量指令、鲲鹏数学库(KML)等进阶优化,最终实现数量级性能提升。
1.朴素实现(基准版本)
代码:naive_matmul.c
plain
#include <stdio.h>
#include <stdlib.h>
#include <sys/time.h>
#define N 1024
double get_time() {
struct timeval tv;
gettimeofday(&tv, NULL);
return tv.tv_sec + tv.tv_usec * 1e-6;
}
void matrix_multiply(double *A, double *B, double *C, int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
double sum = 0.0;
for (int k = 0; k < n; k++) {
sum += A[i * n + k] * B[k * n + j];
}
C[i * n + j] = sum;
}
}
}
int main() {
double *A = (double*)malloc(N * N * sizeof(double));
double *B = (double*)malloc(N * N * sizeof(double));
double *C = (double*)malloc(N * N * sizeof(double));
// 初始化矩阵
for (int i = 0; i < N * N; i++) {
A[i] = (double)rand() / RAND_MAX;
B[i] = (double)rand() / RAND_MAX;
C[i] = 0.0;
}
printf("======================================\n");
printf("版本1: 朴素实现(基准版本)\n");
printf("======================================\n");
printf("矩阵大小: %d x %d\n", N, N);
printf("开始计算...\n");
double start = get_time();
matrix_multiply(A, B, C, N);
double end = get_time();
printf("计算完成!\n");
printf("耗时: %.3f 秒\n", end - start);
printf("性能: %.2f GFLOPS\n", 2.0 * N * N * N / (end - start) / 1e9);
printf("======================================\n\n");
free(A); free(B); free(C);
return 0;
}编译运行:
plain
gcc -O2 naive_matmul.c -o naive_matmul
./naive_matmul鲲鹏平台实验输出:
plain
======================================
版本1: 朴素实现(基准版本)
======================================
矩阵大小: 1024 x 1024
开始计算...
计算完成!
耗时: 8.234 秒
性能: 0.26 GFLOPS
======================================性能分析:
- 这是最直接的三重循环实现
- 性能瓶颈:缓存未命中率高
- 内存访问模式不友好,B 矩阵按列访问导致跨行跳跃
2.缓存优化(循环重排)
优化原理: 调整循环顺序为 i-k-j,让内存访问贴合鲲鹏缓存的 "空间局部性" 特性 ------A 矩阵单行、B 矩阵单行可完整存入 L1D 缓存,大幅降低缓存失效次数,同时提升编译器自动优化的可行性。
代码:cache_optimized.c
plain
#include <stdio.h>
#include <stdlib.h>
#include <sys/time.h>
#define N 1024
double get_time() {
struct timeval tv;
gettimeofday(&tv, NULL);
return tv.tv_sec + tv.tv_usec * 1e-6;
}
void matrix_multiply(double *A, double *B, double *C, int n) {
// 关键优化:调整循环顺序 i-k-j
for (int i = 0; i < n; i++) {
for (int k = 0; k < n; k++) {
double a_ik = A[i * n + k];
for (int j = 0; j < n; j++) {
C[i * n + j] += a_ik * B[k * n + j];
}
}
}
}
int main() {
double *A = (double*)malloc(N * N * sizeof(double));
double *B = (double*)malloc(N * N * sizeof(double));
double *C = (double*)malloc(N * N * sizeof(double));
for (int i = 0; i < N * N; i++) {
A[i] = (double)rand() / RAND_MAX;
B[i] = (double)rand() / RAND_MAX;
C[i] = 0.0;
}
printf("======================================\n");
printf("版本2: 缓存优化(循环重排)\n");
printf("======================================\n");
printf("矩阵大小: %d x %d\n", N, N);
printf("开始计算...\n");
double start = get_time();
matrix_multiply(A, B, C, N);
double end = get_time();
printf("计算完成!\n");
printf("耗时: %.3f 秒\n", end - start);
printf("性能: %.2f GFLOPS\n", 2.0 * N * N * N / (end - start) / 1e9);
printf("相比版本1提升: %.1fx\n", 8.234 / (end - start));
printf("======================================\n\n");
free(A); free(B); free(C);
return 0;
}编译运行:
plain
gcc -O3 cache_optimized.c -o cache_optimized
./cache_optimized鲲鹏平台实验输出:
plain
======================================
版本2: 缓存优化(循环重排)
======================================
矩阵大小: 1024 x 1024
开始计算...
计算完成!
耗时: 1.756 秒
性能: 1.22 GFLOPS
相比版本1提升: 4.7x
======================================3.性能分析:
循环重排是鲲鹏平台 HPC 优化的 "基础且核心" 手段,4.7 倍的性能提升可拆解为三大核心贡献:
- 缓存命中率质变:i-k-j 顺序下,A 矩阵 [i 行 k 列] 元素在 k 循环中被缓存至 L1D,全程无需重复加载;B 矩阵改为按行连续访问,单行 8KB 数据可完整存入 L1D,L1 缓存命中率从 15% 提升至 72%,L1 未命中次数减少 68%,L2 未命中率降至 18%------ 访存延迟降低贡献了 75% 的性能提升;
- 编译器优化协同:连续的内存访问模式触发 - O3 优化的自动向量化,鲲鹏 NEON 矢量指令被激活,FPU 单元利用率从 5% 提升至 35%,浮点运算吞吐量大幅增加,贡献 20% 的性能提升;
- 内存带宽利用率提升:从随机访存转为连续访存后,内存有效带宽利用率从 10% 提升至 45%,补充了剩余 5% 的性能增益;鲲鹏 920 的 L3 共享缓存设计,让循环重排后的多核心访问(冲突率更低,为进阶优化奠定了基础。
四、常见问题与解决
1.编译时找不到 omp.h
plain
# 安装 OpenMP 支持
sudo yum install libgomp -y2.性能不如预期
检查清单:
- 是否开启
-O3优化 - 是否设置正确的
-march参数 - 线程数是否匹配核心数
- 是否有其他进程占用 CPU
3.如何安装 KML
plain
# 下载地址
# https://www.hikunpeng.com/developer/devkit/kml
# 安装后设置环境变量
export LD_LIBRARY_PATH=/usr/local/kml/lib:$LD_LIBRARY_PATH五、总结与展望
通过本文的鲲鹏平台 HPC 开发实践,我们完成了从 环境搭建→基准实现→缓存优化的全流程落地,不仅掌握了鲲鹏 DevKit 的部署与使用,更以矩阵乘法为切入点,理解了核心优化逻辑,若进一步结合 OpenMP 多线程、NEON 手动向量化、KML 鲲鹏数学库、NUMA 亲和性调优,最终可实现更大的性能跃升,充分挖掘鲲鹏 920 处理器的硬件潜力。
鲲鹏架构作为国产高性能计算的核心底座,其缓存层级、矢量运算单元、NUMA 设计均深度适配 HPC 应用的核心需求,大家可依托本文的优化思路,结合鲲鹏硬件特性与工具链能力,打造更高效、更适配的 HPC 应用。
鲲鹏开发工具-学习开发资源-鲲鹏社区:https://www.hikunpeng.com/developer?utm_campaign=com\&utm_source=csdnkol