F. Daniel and Spring Cleaning
二进制数位dp 位运算trick

加起来等于异或,意味着两个数的交等于零。数位dp同时维护两个数的二进制位取什么即可,同时为1无法转移,别的都可以转移
D. Locked Out
调和级数

k x , ( k + 1 ) x ) \[kx,(k+1)x) \[kx,(k+1)x)之间的数都会变成 k x kx kx,我们枚举 x x x,枚举 x x x的所有倍数,然后前缀和统计每一个 \[ k x , ( k + 1 ) x ) \[kx,(k+1)x) \[kx,(k+1)x)里有多少个数字,就能计算出一个 x x x的 s u m ( a ) sum(a) sum(a)。整体是一个调和级数枚举 ## [E. Stairs and Lines](https://codeforces.com/problemset/problem/498/E) 分段矩阵快速幂 状压 dp预处理系数  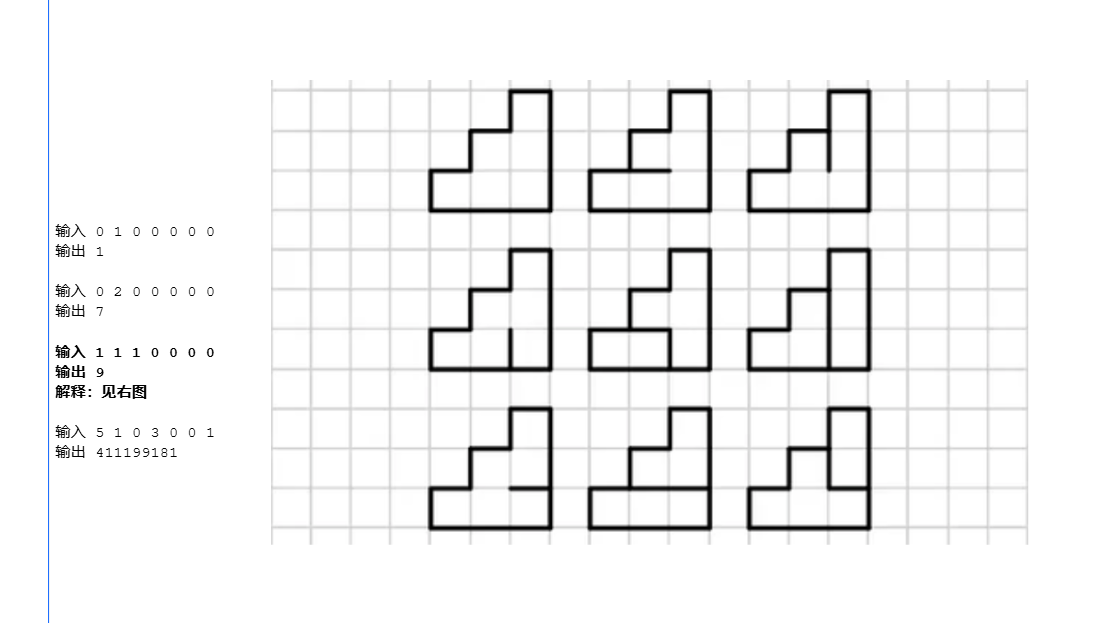 转移是一个 d p dp dp,因为每一列的右边界的选择,之和这一列的左边界有关,是无后效的,故用一个 m a s k mask mask表示第 i i i列的右边界,我们可以枚举这一列的左边界进行转移,确定了左边界还是可以有多种转移,还要考虑这一列的中间的横边的情况,最暴力的就是继续枚举,但把这个问题抽象出来,我们确定了左右两个 m a s k mask mask,中间每个横边可选可不选,问多少种方案使得没有一个格子有四条边,显然可以 d p dp dp解决。 每一段的高度相同,转移都是相同的,考虑快速幂加速转移,转移矩阵的每个位置,对应两个 m a s k mask mask,分别表示这一列的左右边界的情况,接下来跑一个 d p dp dp即可求出这个情况的方案数,也就是转移系数。 但是有多段,两段交界处,列高变了,需要重新构造状态向量和转移矩阵,利用前一段的结果即可构造。 初态和末态都是 m a s k mask mask全一 ## [E. Okabe and El Psy Kongroo](https://codeforces.com/problemset/problem/821/E) 分段快速幂  仍然分段进行快速幂,同时转移就是朴素的网格图路径问题,比较简单 ## [C. Vasya and Basketball](https://codeforces.com/problemset/problem/493/C) 枚举  把两队的所有距离一块排序,显然两个元素中间的区间,取任何值结果都是一样的,所以需要枚举的距离只有 O ( n + m ) O(n+m) O(n+m) ## [E. Power of Points](https://codeforces.com/problemset/problem/1857/E) 扫描线 前缀和  看成有多条线段共享一个端点,每次把这个端点移动一下,求线段长度和?类似于扫描线前缀和的思想,维护两侧的线段个数,和线段和,移动可以 O ( 1 ) O(1) O(1)更新线段和 ## [D. Right Left Wrong](https://codeforces.com/problemset/problem/2000/D) 贪心  每次选一个区间,消掉,获得区间和。每次选最左侧 L L L和最右侧 R R R是最优的。 如果 \[ L 1 , L 2 , R 1 , R 2 \] \[L_1,L_2,R_1,R_2\] \[L1,L2,R1,R2\]这样配对,两个区间有交集,消除完一个区间后另一个就不能消除了,不如 \[ L 1 , R 2 \] \[L_1,R_2\] \[L1,R2\]优 如果 \[ L 1 , R 1 , 0 , 0 , 0 , L 2 , R 2 \] \[L_1,R_1,0,0,0,L_2,R_2\] \[L1,R1,0,0,0,L2,R2\],两个各自配对,中间这一段 0 0 0的元素值则无法加入,不如 \[ L 1 , R 2 \] \[L_1,R_2\] \[L1,R2\]优 相向双指针分别从开头结尾开始维护下一个 L , R L,R L,R即可