预测概率的先验校准

zhb20002025-07-13 14:19

目录

在知乎上也发了一份：https://zhuanlan.zhihu.com/p/1926078272694878598

为什么需要校准？

在很多场景中，我们不仅关心模型输出的预测类别，还关心模型输出的预测概率，然而模型输出的预测概率未必等于真实的概率。概率校准就是重新计算预测概率，以让它尽量接近真实的概率。

预测概率不准确经常出现在点击率预估、风控等场景中，主要原因与训练数据有关。在一些实际场景中，例如广告/推荐系统的点击率预估、金融反欺诈、医疗诊断，正负样本的比例极度不均衡。例如，广告的点击率可能只有 1%，而 99% 都是未点击。

直接用这样高度不平衡的数据训练模型，会遇到两个问题：

  1. 模型预测偏向多数类：模型可能学到一个"捷径"，即总是预测多数类（如"不点击"），这样也能获得很高的准确率（Accuracy），但对于我们关心的少数类（"点击"）的识别能力很差。
  2. 训练效率低：大量的负样本提供了冗余信息，增加了训练的计算开销。

为了解决这个问题，一个常见的训练策略是对负样本欠采样 （Undersampling）。比如，我们保留所有正样本，但只从负样本中随机抽取 \(r = 10\%\) 进行训练。

这样做的后果是：我们人为地改变了训练数据中正负样本的比例。模型在训练时看到的是一个虚假的世界 ，在这个虚假的采样世界中，正负样本之比远高于现实世界。因此，模型预测出的正样本概率 \(p' = P'(y=1|x)\) 是基于这个采样后的数据分布的，而不是真实世界的分布。如果不加校准，这个预测概率 \(p'\) 是不准确的、偏高的，不能直接用于业务决策。

这里用 \(p\) 表示真实世界的数据分布下的概率，\(p'\) 表示采样世界的数据分布下的概率，\(r\) 表示负样本的采样率（r = 采样后的负样本数 / 原始负样本数）。

校准的目的：将模型在采样数据上学到的概率 \(p'\)（\(P'(y=1|x)\) 的简写），校准回它在真实数据分布下应有的概率 \(p\)（\(P(y=1|x)\) 的简写）。

应用贝叶斯定理

根据贝叶斯定理，一个事件的后验概率可以表示为：

\[P(A|B) = \frac{P(A)P(B|A)}{P(B)}. \]

我们将贝叶斯定理应用到我们的真实分布和采样后分布上。

在真实分布下：

\[P(y=1|x) = \frac{P(y=1)P(x|y=1)}{P(x)}, \]

\[P(y=0|x) = \frac{P(y=0)P(x|y=0)}{P(x)}, \]

两者相除，得到真实世界中后验概率的 odds，记为 \(o\)：

\[o = \frac{P(y=1|x)}{P(y=0|x)} = \frac{P(x|y=1)P(y=1)}{P(x|y=0)P(y=0)}. \]

在采样后的分布下：

\[P'(y=1|x) = \frac{P'(y=1)P'(x|y=1)}{P'(x)}, \]

\[P'(y=0|x) = \frac{P'(y=0)P'(x|y=0)}{P'(x)}, \]

两者相除，得到采样世界中后验概率的 odds，记为 \(o'\)：

\[o' = \frac{P'(y=1|x)}{P'(y=0|x)} = \frac{P'(x|y=1)P'(y=1)}{P'(x|y=0)P'(y=0)}. \]

注：Odds 又称几率或概率比，表示一个事件发生的概率与不发生的概率之比。

建立两个世界的联系

现在，我们来分析真实世界 odds 和采样世界 odds 中各项之间的关系。

(1) 似然（Likelihood） \(P(x|y)\)：

\(P'(x|y=1) = P(x|y=1)\)：我们保留了所有的正样本，所以对于正样本，其类内样本分布没有改变。

\(P'(x|y=0) = P(x|y=0)\)：我们对负样本是随机欠采样的，因此我们认为，对于负样本，其类内样本分布也基本上没有改变。

(2) 先验（Prior） \(P(y)\)：

先验概率正是我们通过采样改变的东西。

我们同样用 odds 的方式表达采样世界与真实世界的先验概率的关系，它们满足如下比例关系：

\[\frac{\frac{P'(y=1)}{P'(y=0)}}{\frac{P(y=1)}{P(y=0)}} = \frac{1}{r}. \]

这个比例关系从直观上很容易理解，先验概率的 odds \(\frac{P(y=1)}{P(y=0)}\) 就是正样本数量与负样本数量之比，采样后的负样本数量被乘上了 \(r\)，因此采样后的先验概率 odds \(\frac{P'(y=1)}{P'(y=0)}\) 是真实世界的先验概率 odds \(\frac{P(y=1)}{P(y=0)}\) 的 \(\frac{1}{r}\)。

推导校准公式

有了上面的比例关系，我们用两个世界中后验概率 odds 之比来推导校准公式：

\[\begin{aligned} \frac{o'}{o} & = \frac{\frac{P'(y=1|x)}{P'(y=0|x)}}{\frac{P(y=1|x)}{P(y=0|x)}} = \frac{\frac{P'(x|y=1)P'(y=1)}{P'(x|y=0)P'(y=0)}}{\frac{P(x|y=1)P(y=1)}{P(x|y=0)P(y=0)}} \\ & = \frac{\frac{P'(y=1)}{P'(y=0)}}{\frac{P(y=1)}{P(y=0)}} = \frac{1}{r}. \end{aligned} \]

于是我们得到了一个非常简洁优美的关系：

\[o = o' \cdot r. \]

我们的目标是得到校准公式，即用 \(p'\) 来计算 \(p\)，因此现在我们将几率（Odds）转换回概率（Probability）。Odds 表示为正样本后验概率与负样本后验概率之比：

\[o' = \frac{p'}{1 - p'}, \quad o = \frac{p}{1 - p}, \]

代入上面的关系：

\[\frac{p}{1 - p} = \frac{p'}{1 - p'} \cdot r, \]

解出 \(p\)：

\[p = \frac{p'}{p' + \frac{1 - p'}{r}}. \]

这就是最终的先验校准公式。

直观理解

让我们来直观地理解这个公式：

\[p = \frac{p'}{p' + \frac{1 - p'}{r}}, \]

在采样世界中，\(p'\) 是模型认为的"是正样本"的"证据"，\(1 - p'\) 是模型认为的"是负样本"的"证据"。正样本的后验概率可以视为正样本"证据"与总"证据"的比值，即：

\[\text{正样本后验概率} = \frac{\text{正样本"证据"}}{\text{正样本"证据"} + \text{负样本"证据"}}, \]

\[p' = \frac{p'}{p' + (1 - p')}. \]

但我们知道，负样本被我们欠采样了，其数量只占原来的 \(r\)，为了还原真相，我们需要把负样本的"证据"给放大回去。怎么放大？就是除以采样率 \(r\)。所以，校准后的负样本"证据"为 \(\frac{1 - p'}{r}\)，正样本"证据"仍然为 \(p'\)。

最后，我们用这个新的"证据"计算正样本的后验概率，就得到了校准后的概率 \(p\)：

\[p = \frac{p'}{p' + \frac{1 - p'}{r}}. \]

将先验校准融入偏置

在逻辑回归中，先验校准可以融入模型的偏置项（Bias）中。

Logistic 函数的形式为：

\[p' = \frac{1}{1 + e^{-z}} = \frac{e^z}{1 + e^z}, \]

其中 \(z\) 被称为 logit。Logit 就是 log of odds，即

\[z = \log\frac{p'}{1 - p'}, \]

而 \(e^z\) 就是 odds。

我们观察到先验校准公式中很容易凑出 odds（即 \(\frac{p'}{1 - p'}\)）的形式：

\[\begin{aligned} p & = \frac{p'}{p' + \frac{1 - p'}{r}} \\ & = \frac{\frac{p'}{1 - p'}}{\frac{p'}{1 - p'} + \frac{1}{r}} = \frac{e^z}{e^z + \frac{1}{r}} \\ & = \frac{1}{1 + \frac{1}{e^z \cdot r}} = \frac{1}{1 + (e^{z - \log r})^{-1}} \\ & = \frac{1}{1 + e^{-(z + \log r)}}. \end{aligned} \]

因此只需要往模型的偏置项中加上一个 \(\log r\) 就可以实现先验校准，无需额外的计算和修正步骤。

从这里我们也可以看出，由于先验校准与修改模型的 bias 项等价，因此先验校准是保序 的，即它不会改变模型对样本打分的序，因此先验校准不会影响 AUC 指标。

代码实践

接下来，我们将通过一个简单的例子演示先验校准的效果。以下实验代码建议在 Jupyter Notebook 中运行。

(1) 准备工作

python 复制代码 
import copy
import torch
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score, roc_auc_score
import matplotlib.pyplot as plt

# device = torch.device('cuda')
device = torch.device('cpu')
print(f'使用的设备是: {device}')

(2) 生成模拟数据集

模拟一个正负类别极度不均衡的"真实"数据集，其中正样本非常稀少。

你可以认为这是在模拟一个点击率预估（CTR）场景，其中正样本（点击）非常稀少，绝大部分样本都是负样本（未点击）。

python 复制代码 
def create_dataset(
    n_samples: int,
    weights: list[float],
    random_state: int = 42
) -> tuple[torch.Tensor, torch.Tensor]:
    """
    使用 sklearn 创建一个二分类数据集

    :param n_samples: 样本数量
    :param weights: 类别权重，例如 [0.99, 0.01] 表示 99% 的负样本和 1% 的正样本
    :param random_state: 随机种子
    """
    X, y = make_classification(
        n_samples=n_samples,
        n_features=20,
        n_informative=10,
        n_redundant=5,
        n_classes=2,
        weights=weights,
        flip_y=0.05,
        random_state=random_state
    )
    X = torch.tensor(X, dtype=torch.float32)
    y = torch.tensor(y, dtype=torch.int64)
    return X, y


# 创建真实的全量数据集
X_full, y_full = create_dataset(n_samples=100000, weights=[0.99, 0.01])

# 计算并打印真实数据集的统计信息
true_positive_rate = y_full.float().mean().item()
print(f'--- 真实数据集信息 ---')
print(f'总样本数: {len(y_full)}')
print(f'正样本数: {(y_full == 1).sum().item()}')
print(f'负样本数: {len(y_full) - y_full.sum().item()}')
print(f'真实正样本率 (真实 p): {true_positive_rate:.4f}')

输出：

Plain 复制代码 
--- 真实数据集信息 ---
总样本数: 100000
正样本数: 3445
负样本数: 96555
真实正样本率 (真实 p): 0.0344

(3) 负样本欠采样

为了高效训练，我们对负样本进行欠采样，这会"扭曲"训练集中的正负样本比例。

python 复制代码 
def undersample_negatives(
    X: torch.Tensor,
    y: torch.Tensor,
    sampling_rate: float
) -> tuple[torch.Tensor, torch.Tensor]:
    """
    对负样本 (y=0) 进行欠采样

    :param sampling_rate: 负样本采样率 (r)
    """
    pos_indices = (y == 1).nonzero(as_tuple=True)[0]
    neg_indices = (y == 0).nonzero(as_tuple=True)[0]
    # 从负样本中随机抽取一部分
    n_neg_sampled = int(len(neg_indices) * sampling_rate)
    sampled_neg_indices = neg_indices[torch.randperm(len(neg_indices))[:n_neg_sampled]]
    # 合并正样本和采样后的负样本
    all_indices = torch.cat([pos_indices, sampled_neg_indices])   
    # 打乱顺序
    all_indices = all_indices[torch.randperm(len(all_indices))]
    return X[all_indices], y[all_indices]


# r: 负样本采样率
NEG_SAMPLE_RATE_R = 0.1
# 生成用于训练的欠采样数据集
X_train, y_train = undersample_negatives(X_full, y_full, NEG_SAMPLE_RATE_R)

# 计算并打印训练数据集的统计信息
train_positive_rate = y_train.float().mean().item()
print(f'--- 欠采样训练集信息 ---')
print(f'负样本采样率 (r): {NEG_SAMPLE_RATE_R}')
print(f'训练集总样本数: {len(y_train)}')
print(f'训练集正样本数: {y_train.sum().item():.0f}')
print(f'训练集负样本数: {len(y_train) - y_train.sum().item()}')
print(f"训练集正样本率 (失真 p'): {train_positive_rate:.4f}")

输出：

Plain 复制代码 
--- 欠采样训练集信息 ---
负样本采样率 (r): 0.1
训练集总样本数: 13100
训练集正样本数: 3445
训练集负样本数: 9655
训练集正样本率 (失真 p'): 0.2630

(4) 模型定义与训练

这里我们使用一个简单的逻辑回归模型，在采样后的训练集上进行训练。

python 复制代码 
class LogisticRegression(torch.nn.Module):
    def __init__(self, input_dim: int):
        super().__init__()
        self.linear = torch.nn.Linear(input_dim, 1)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        # 输出原始的 logits，不经过 sigmoid
        return self.linear(x).squeeze(dim=-1)


def train_model(
    model: torch.nn.Module,
    X: torch.Tensor,
    y: torch.Tensor,
    device: torch.device,
    epochs: int,
    lr: float,
):
    """训练函数"""
    X, y = X.to(device), y.to(device)
    optimizer = torch.optim.SGD(model.parameters(), lr=lr, momentum=0.9, weight_decay=1e-3)
    model.train()
    for epoch in range(epochs):
        optimizer.zero_grad()
        logits = model(X)
        loss = torch.nn.functional.binary_cross_entropy_with_logits(logits, y.float())
        loss.backward()
        optimizer.step()
        if (epoch + 1) % 100 == 0:
            print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')


# --- 训练模型 ---
model = LogisticRegression(input_dim=X_train.size(1))
print('开始在采样数据集上训练模型...')
train_model(model, X_train, y_train, epochs=500, lr=0.01, device=device)
print('训练完成！')

输出：

Plain 复制代码 
开始在采样数据集上训练模型...
Epoch [100/500], Loss: 0.5467
Epoch [200/500], Loss: 0.5459
Epoch [300/500], Loss: 0.5458
Epoch [400/500], Loss: 0.5457
Epoch [500/500], Loss: 0.5457
训练完成！

(5) 评估校准前的模型

用训练好的模型在真实全量数据上预测，其平均预测概率会远高于真实的正样本率。

python 复制代码 
def get_predictions(model: torch.nn.Module, X: torch.Tensor) -> torch.Tensor:
    """获取模型预测的概率"""
    model.eval()
    with torch.no_grad():
        X = X.to(device)
        logits = model(X)
        probs = torch.sigmoid(logits)
    return probs.cpu()


# 获取校准前的预测概率
probs_before_correction = get_predictions(model, X_full)
avg_prob_before = probs_before_correction.mean()
print('--- 校准前评估 (在全量数据上) ---')
print(f'校准前模型的平均预测概率: {avg_prob_before:.4f}')
print(f'真实正样本率: {true_positive_rate:.4f}')
print()
print(f'校准前模型的准确率: {accuracy_score(y_full, (probs_before_correction > 0.5).int()):.4f}')
print(f'校准前模型的 AUC: {roc_auc_score(y_full, probs_before_correction):.4f}')

输出：

Plain 复制代码 
--- 校准前评估 (在全量数据上) ---
校准前模型的平均预测概率: 0.2484
真实正样本率: 0.0344

校准前模型的准确率: 0.9655
校准前模型的 AUC: 0.6150

结论：模型的预测概率严重偏高，因为它是在正样本比例被人为提高的数据集上训练的。

(6) 实施先验校准

python 复制代码 
# 获取原始 bias
print(f'原始 Bias: {model.linear.bias.item():.4f}')

# 计算校准项 log(r)
# 注意：r 是负样本采样率，不是正样本率
correction_term = torch.log(torch.tensor(NEG_SAMPLE_RATE_R, dtype=torch.float32))
print(f'校准项 log(r): {correction_term.item():.4f}')

# 应用先验校准
calibrated_model = copy.deepcopy(model)
calibrated_model.linear.bias.data += correction_term.to(device)
print(f'校准后 Bias: {calibrated_model.linear.bias.item():.4f}')

输出：

Plain 复制代码 
原始 Bias: -0.5210
校准项 log(r): -2.3026
校准后 Bias: -2.8236

(7) 评估校准后的模型

再次在全量数据上进行评估，可以看到校准后的平均预测概率已经非常接近正样本率的真实值。

python 复制代码 
# 获取校准后的预测概率
probs_after_correction = get_predictions(calibrated_model, X_full)
avg_prob_after = probs_after_correction.mean()

print('--- 校准后评估 (在全量数据上) ---')
print(f'校准后模型的平均预测概率: {avg_prob_after:.4f}')
print(f'真实正样本率: {true_positive_rate:.4f}')
print()
print(f'校准后模型的准确率: {accuracy_score(y_full, (probs_after_correction > 0.5).int()):.4f}')
print(f'校准后模型的 AUC: {roc_auc_score(y_full, probs_after_correction):.4f}')

输出：

Plain 复制代码 
--- 校准后评估 (在全量数据上) ---
校准后模型的平均预测概率: 0.0337
真实正样本率: 0.0344

校准后模型的准确率: 0.9656
校准后模型的 AUC: 0.6150

结论：经过先验校准，模型的平均预测概率被成功修正，与真实概率基本一致。

此外可以注意到，校准前后模型的 AUC 指标保持不变，因为先验校准不会改变模型对样本打分的序。

(8) 可视化对比

画出校准前后的预测概率分布图。

python 复制代码 
import matplotlib
# 让 matplotlib 支持中文显示，macOS 上可设置为 'Arial Unicode MS' 等字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False  # 正常显示负号

plt.figure(figsize=(8, 5), dpi=300)
# 绘制校准前概率分布
plt.hist(
    probs_before_correction,
    color='skyblue',
    label=f'校准前 (均值={avg_prob_before:.4f})',
    density=True,
    bins=100
)
# 绘制校准后概率分布
plt.hist(
    probs_after_correction,
    color='lightgreen',
    label=f'校准后 (均值={avg_prob_after:.4f})',
    density=True,
    bins=100
)
# 绘制真实概率的垂线
plt.axvline(
    true_positive_rate,
    color='red',
    linestyle='--',
    linewidth=2,
    label=f'真实概率均值 ({true_positive_rate:.4f})'
)

plt.title('先验校准效果对比', fontsize=16)
plt.xlabel('模型预测概率', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
plt.show()

输出：

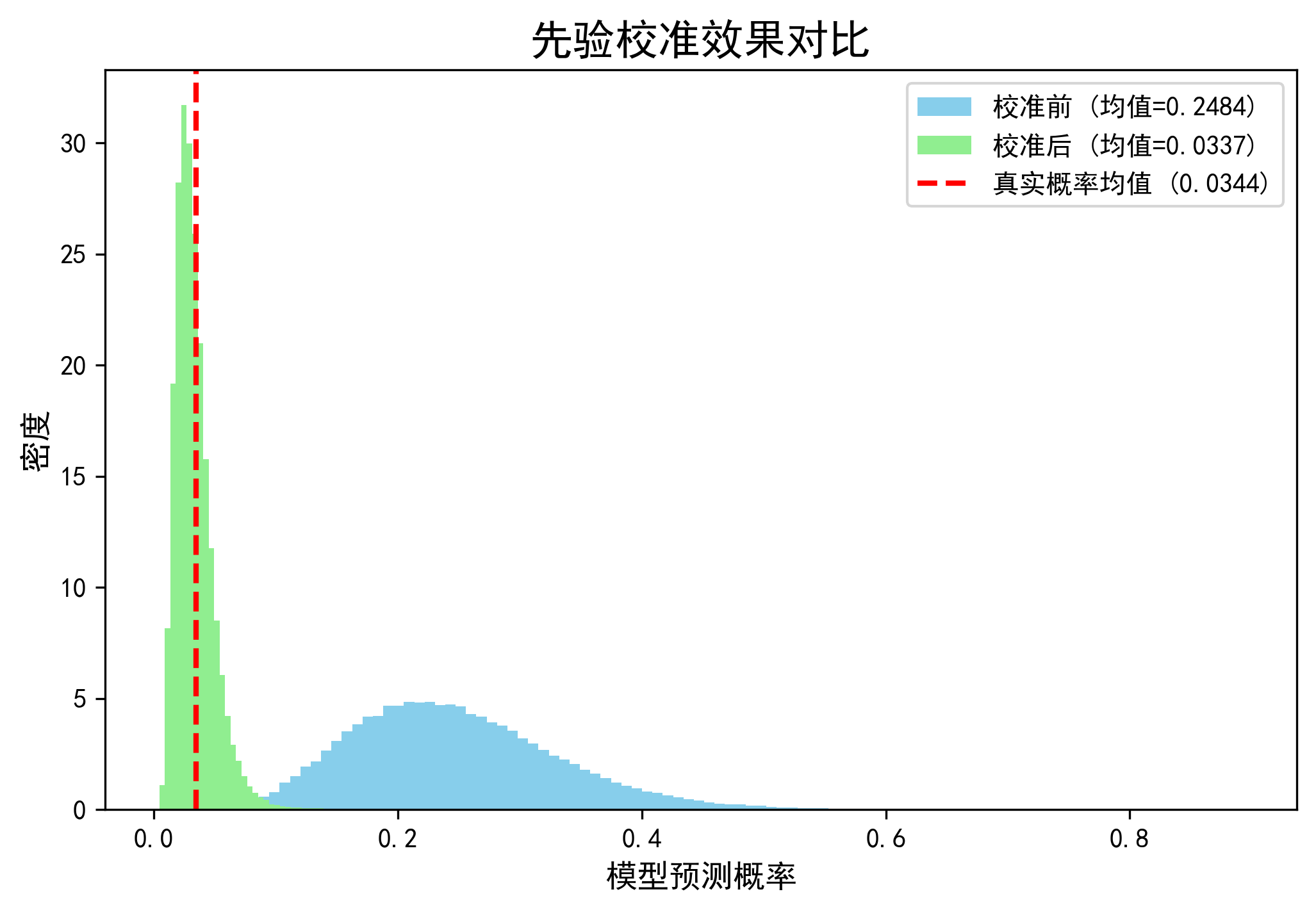
可视化结果解读：

  • 蓝色直方图（校准前）: 整个概率分布严重右偏，其均值（模型预估的整体点击率）远高于红色的真实概率线。
  • 橙色直方图（校准后）: 整个概率分布向左移动，其均值几乎与红色的真实概率线重合。
  • 红色虚线（真实概率）: 代表了在全量数据上我们期望模型达到的平均预测概率。

上述实验结果清晰地表明，先验校准技术能够有效地修正因样本采样不均衡而导致的模型预测偏差，让模型输出的预测概率在统计意义上更具解释性。

相关推荐
铸剑师欧冶子几秒前
AI领域的黄埔军校：OpenAI是新一代的PayPal Mafia，门生故吏遍天下
人工智能·深度学习·机器学习·gpt-3·文心一言
安特尼2 小时前
Datawhale AI夏令营：基于带货视频评论的用户洞察挑战赛
机器学习·语言模型·音视频
DAWN_T172 小时前
Transforms
pytorch·python·机器学习·jupyter·pycharm
一百天成为python专家3 小时前
python库之jieba 库
开发语言·人工智能·python·深度学习·机器学习·pycharm·python3.11
Blossom.1183 小时前
用一张“冰裂纹”石墨烯薄膜，让被动散热也能做 AI 推理——基于亚波长裂纹等离激元的零功耗温度-逻辑门
人工智能·深度学习·神经网络·目标检测·机器学习·机器人·语音识别
计算生物前沿5 小时前
单细胞分析教程 | （二）标准化、特征选择、降为、聚类及可视化
人工智能·机器学习·聚类
超龄超能程序猿5 小时前
(5)机器学习小白入门 YOLOv：数据需求与图像不足应对策略
人工智能·python·机器学习·numpy·pandas·scipy
cwn_6 小时前
回归（多项式回归）
人工智能·机器学习·数据挖掘·回归
优乐美香芋味好喝7 小时前
2025年7月11日学习笔记&一周归纳——模式识别与机器学习
笔记·学习·机器学习
众链网络7 小时前
AI进化论08：机器学习的崛起——数据和算法的“二人转”，AI“闷声发大财”
人工智能·算法·机器学习
热门推荐
01KGG转MP3工具|非KGM文件|解密音频02集群聊天服务器---MySQL数据库的建立03Coze扣子平台完整体验和实践（附国内和国际版对比）04全球最强模型Grok4，国内已可免费使用！（附教程）05使用Ruby接入实时行情API教程06扣子（coze）实战|我用扣子搭建了一个自动分析小红薯笔记内容的AI应用|详细步骤拆解07【无标题】08基于odoo17的设计模式详解---单例模式09DeepSeek各版本说明与优缺点分析10绿色建筑新态势：楼宇自控助力能效提升，推动成本优化新路径