
文章目录
-
- 从感知机到神经网络
- 1,神经网络到底有几层?
- [2,感知机 vs 神经网络:激活函数的作用](#2,感知机 vs 神经网络:激活函数的作用)
- 3,激活函数:阶跃函数、sigmoid函数与ReLU函数
- 4,多维数组的运算(重点是广播机制)
-
- [(4, 1)和(4,)的区别](#(4, 1)和(4,)的区别)
- 5,神经网络实现中的矩阵运算
- 6,输出层的设计:
- 7,牛刀小试:手写数字识别
- 8,本章小结
从感知机到神经网络
1,神经网络到底有几层?
所谓的层数,如何定义,是直接从表面形式上去看,某个网络有几层神经元吗?比如说下面这个简单的MLP有3层。
还是从实际上具有权重的神经元,我们才把它定义为一层,我们只看输入指向有权重的神经元数,有几层输入是有权重调整的,我们才定义这个是一层?
其实从哲学层面上讲,后者的定义是我们只要有功能的神经元,也就是能够对输入进行加权+偏置处理的神经元,相当于我们类比神经生物学上的定义,我们只把能够执行------将上一个输入的突出前膜的电信号,转换为突触后膜的化学信号的功能------的神经元,才认为是在大脑神经元交织的网络中有实际作用的神经元,然后才算进去一层。
简而言之:
在计算 神经网络的层数时,只计算具有计算能力的层,而输入层只是将数据进行输入,无计算过程,所以层数:隐藏层层数+1个输出层。

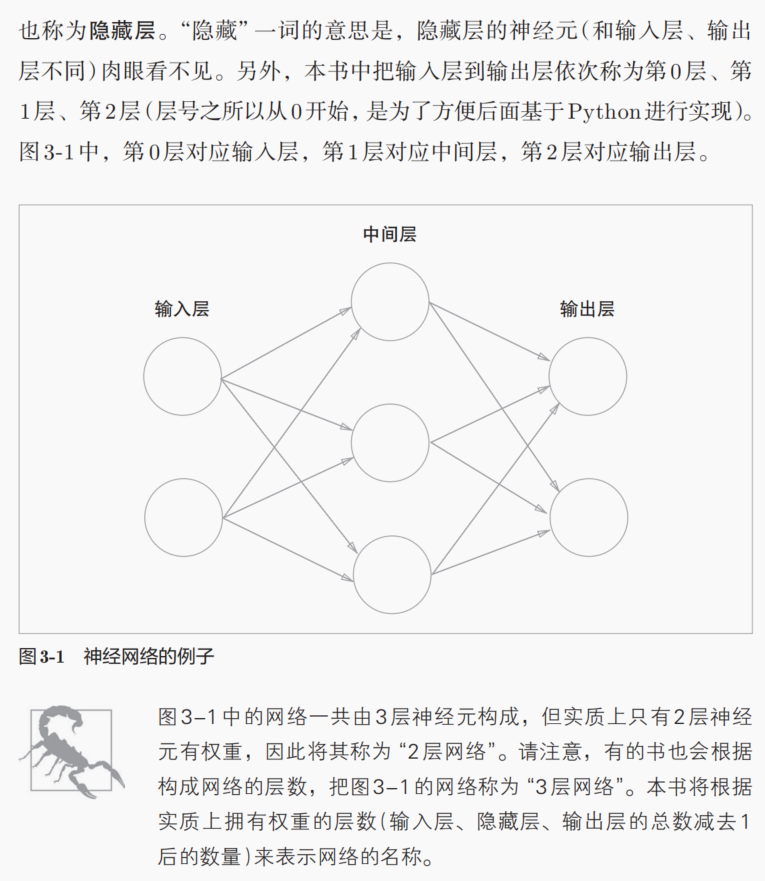

如何确定神经网络的层数以及隐藏层中的神经元数目?
分享一篇知乎上的文章:https://zhuanlan.zhihu.com/p/100419971
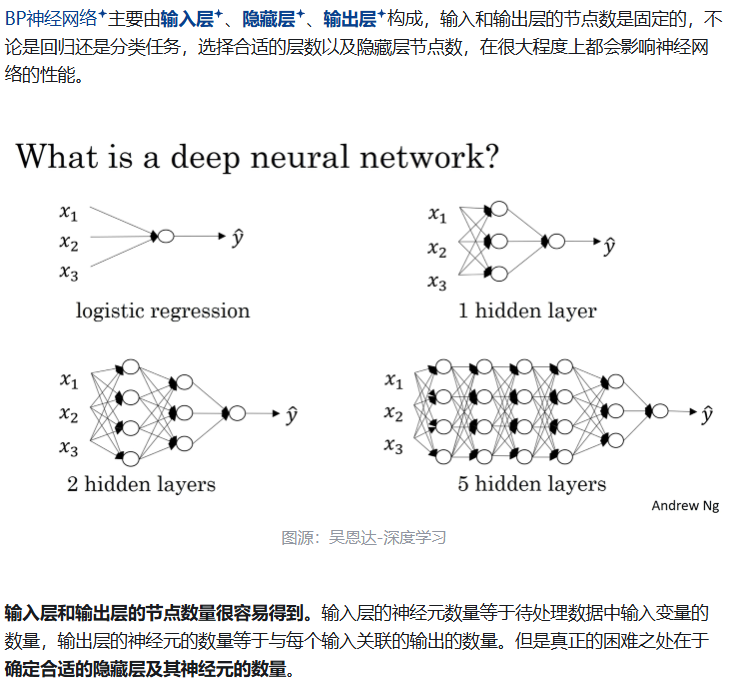



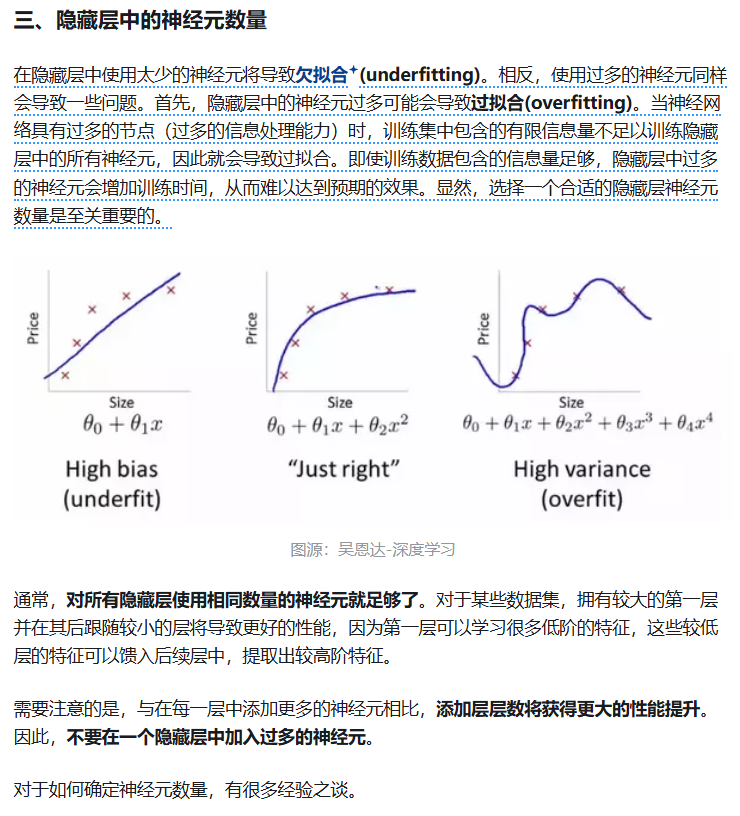

一提到隐藏层中神经元数目,就不得不提经典机器学习中的过拟合问题了。
我们一般认为的过拟合,
从model角度来讲,无非是model太复杂了(参数太多,至少相对于训练样本来说的规模),也就是model太灵活了,太flexible了。
我一般简单理解的话,就是model太复杂,然后就会导致在拟合训练数据的时候出现high variance高方差,low bias低偏差的情况(可以参考我之前总结经典机器学习时MSE的bias-var偏差-方差分解)
https://blog.csdn.net/weixin_62528784/article/details/148594466?spm=1001.2014.3001.5501
model太复杂的话,就相当于是有很大一部分自由度/灵活度(比如说神经网络中一大部分的神经元,就是一大部分冗余的参数),本来参数少的时候就可以拟合我们想要学习到的真实数据的规律(y~x),当然我们知道数据测量的时候会有误差,这一部分误差可能是因为系统误差或者是其他的原因,总之我们的数据一般是y=f(x)+error,然后我们一般很少的参数就可以学习到其中的函数关系f(x),也就是数据真实的规律了;
但是就是因为model太灵活了,一大部分冗余的参数有了很大的自由度,可以学习到这一部分error的信息,也就是将这部分noise也当做是f(x)内需要学习的知识,结果就会导致model会拟合每一个数据点。
从结果角度来讲,过拟合的效果就是train集上error小,但是test集上error却反而很大(可以参考李宏毅老师机器学习课程对于model训练可能问题类型的分类那一节课)。
------》如果要对刚入门的本科学生一句话解释什么是过拟合,我一般会直接解释为 输入data维度小于model的参数维度等原因,导致model对训练data的拟合过于复杂(当然有点以偏概全了,仅作参考)。
过拟合并不仅仅是因为输入数据维度小于模型的参数维度,但这种情况确实是一个重要的因素。过拟合通常发生在模型对训练数据的拟合过于复杂,以至于它不仅学习到了数据中的真实规律,还学习到了训练数据中的噪声和随机波动,从而导致模型在新的、未见过的数据上表现不佳。关键因素有很多:
- 模型复杂度过高
- 参数数量过多:当模型的参数数量(如神经网络中的权重和偏置)远大于输入数据的维度时,模型有足够的自由度去"记住"训练数据中的每一个细节,包括噪声。例如,一个简单的线性回归模型可能不会过拟合,但如果使用一个具有成千上万个参数的深度神经网络来拟合少量数据,就很容易过拟合。
- 隐藏层神经元过多:在神经网络中,隐藏层的神经元数量过多会增加模型的复杂度。如果隐藏层的神经元数量过多,模型可能会学习到训练数据中的噪声,而不是数据的真实分布。
- 训练数据量不足
- 当训练数据的样本数量较少时,模型很难从有限的数据中学习到通用的规律。如果模型复杂度很高,它可能会过度拟合这些有限的数据样本,从而导致过拟合。例如,如果只有10个数据点,但模型有100个参数,模型可能会完美拟合这10个点,但对新的数据毫无泛化能力。
- 数据噪声和随机性
- 训练数据中可能包含噪声(如测量误差、数据录入错误等)。如果模型复杂度很高,它可能会将这些噪声当作真实的规律来学习。例如,一个简单的线性关系可能因为数据中的噪声而被拟合为一个复杂的曲线。
- 模型训练时间过长
- 即使模型的复杂度适中,但如果训练时间过长,模型可能会逐渐学习到训练数据中的噪声。在实际应用中,通常会设置早停(early stopping)机制,即在验证集的性能不再提升时停止训练,以防止过拟合。
- 输入数据维度小于模型的参数维度
- 这是过拟合的一个常见场景,但并不是唯一原因。当输入数据的维度(特征数量)远小于模型的参数数量时,模型很容易过拟合。例如,一个只有10个特征的数据集,如果使用一个具有数百万参数的深度神经网络来拟合,模型可能会过度拟合这些特征的组合。
如何避免过拟合?
为了避免过拟合,可以采取以下措施:
- 增加训练数据量:更多的数据可以帮助模型学习到更通用的规律。
- 简化模型:减少模型的复杂度,例如减少隐藏层神经元的数量或层数。
- 正则化:使用L1或L2正则化限制模型的权重大小,防止模型过于复杂。
- 早停机制:在训练过程中监控验证集的性能,一旦性能不再提升就停止训练。
- 数据增强:通过数据增强技术(如旋转、缩放、噪声注入等)增加训练数据的多样性。
- Dropout:在训练过程中随机丢弃一部分神经元,防止模型过度依赖某些特定的神经元。
2,感知机 vs 神经网络:激活函数的作用

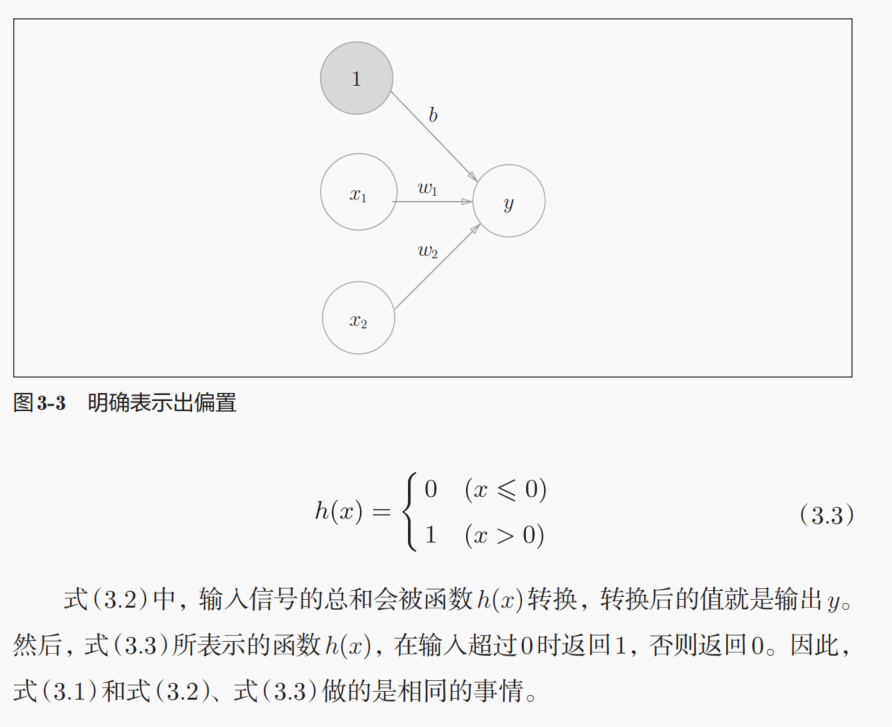
偏置也可以用神经元来表示。

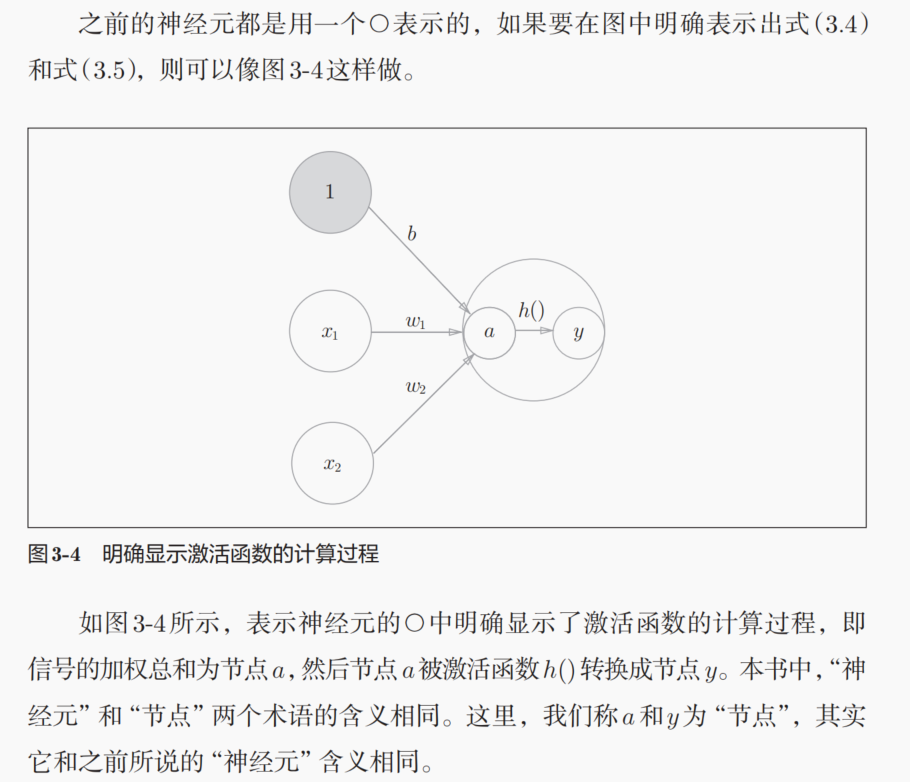
我们在理解激活函数这一个过程的时候,其实是倾向于将激活函数放在神经元内部进行处理的,也就是说区别与权重和偏置等参数,后者我们一般是放在神经元之间的信号传递上去理解,而不是放在神经元所在的层去理解;
但是前者,也就是激活函数,我们是倾向于认为是在神经元所在层中进行的处理。类比生物学中的神经元来讲,每一个神经元之间的信号处理以及传递作用,其实是在突触前膜到突触后膜之间的时空坐标中进行的生物学过程,但是激活函数,也就是传递到突触后膜上的化学信号(离子浓度)是否达到指定的通道蛋白的浓度阈值,这个才是对应着激活函数的,然后这个过程实际上也是发生在后面一个神经元上的,这个是从生物学过程中的空间先验知识进行的理解。
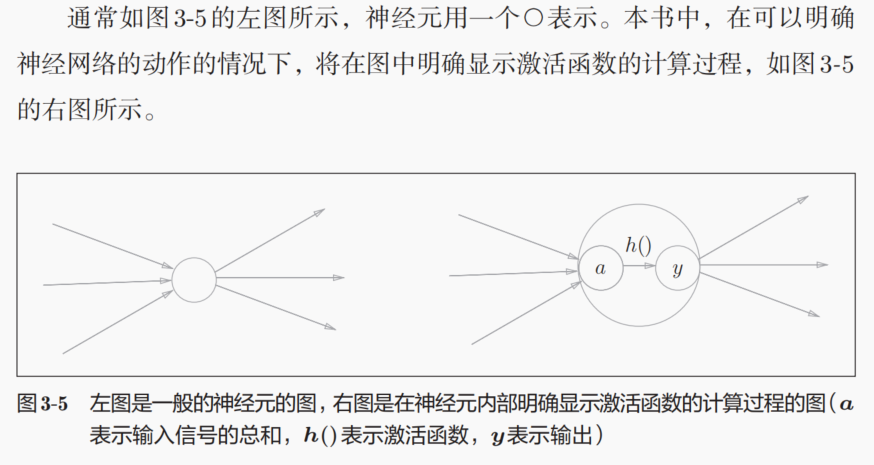

简单来说,单层感知机(朴素感知机)是使用非平滑激活函数,然后MLP也就是神经网络使用了平滑的激活函数。
3,激活函数:阶跃函数、sigmoid函数与ReLU函数


(1)单值输入与多值输入(tensor张量输入)信号的激活


只能说恰好是阶跃函数的输出是1或者是0,而逻辑运算的转换又恰好可以是转换为1或者是0,所以可以直接使用逻辑运算的结果进行一个数值输出的转换;
而且需要注意输入以及输出的数据类型到底是什么,在使用astype的时候可以使用dtype属性查看一下输入数据的具体的数据类型;
注意这里并没有np.int类型的数据,得使用np.int64类型
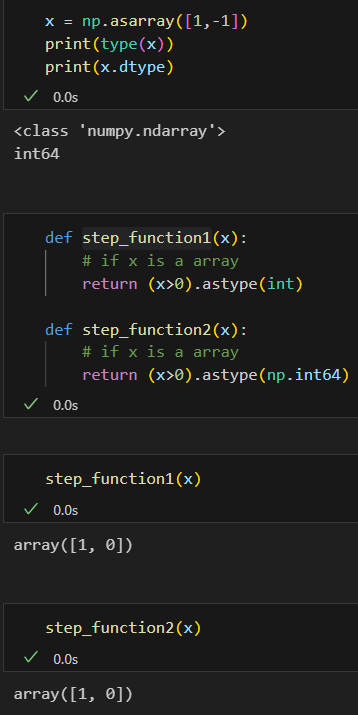

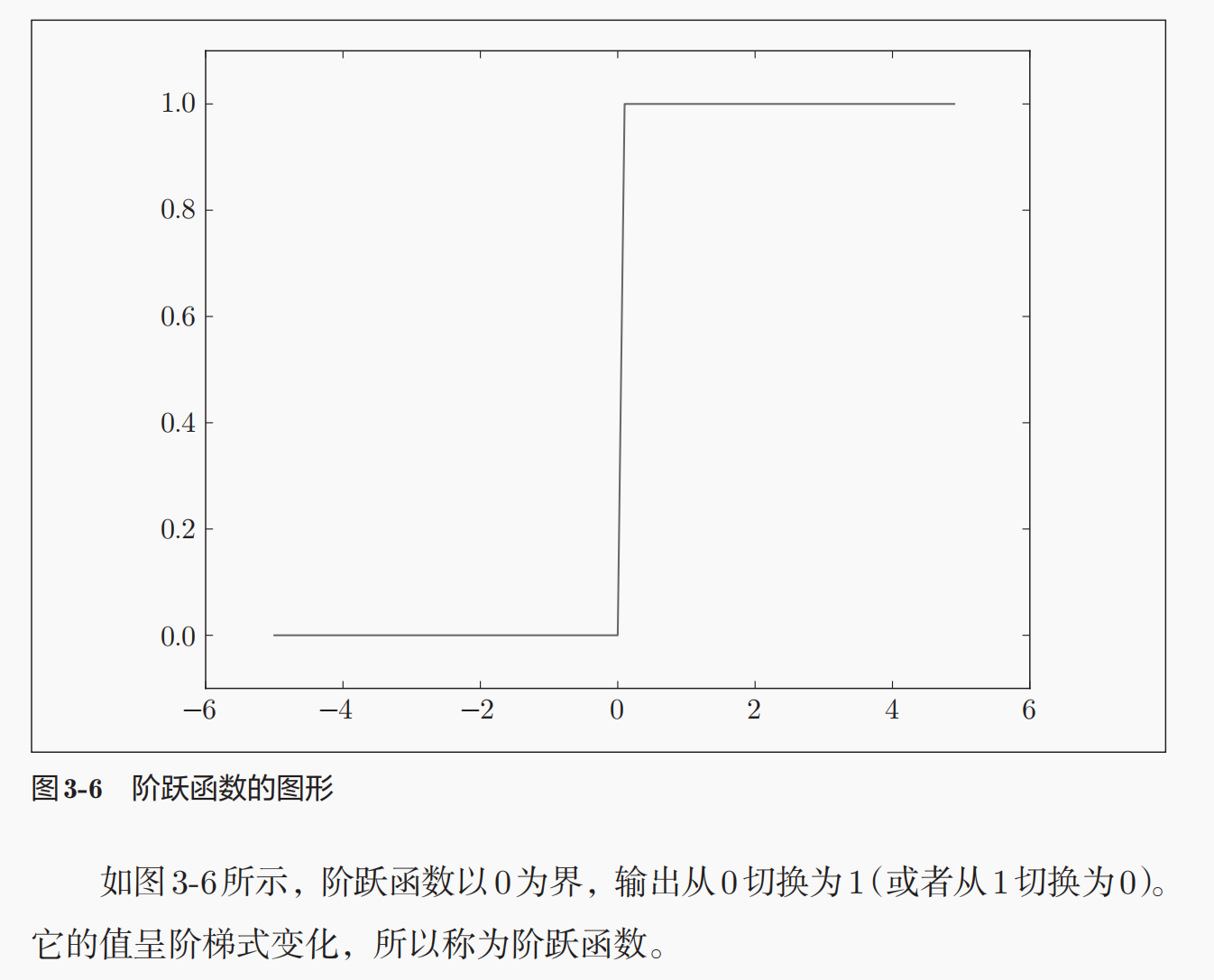
python
import numpy as np
import matplotlib.pyplot as plt
# 首先是需要定义1个激活函数,也就是此处的阶跃函数
def step_function(x):
return (x>0).astype(np.int64)
# 定义输入的数据,可以是1个序列数据
x = np.arange(-5.0,5.0,0.1)
# 然后计算激活函数的输出
y = step_function(x)
# 可以绘制对应激活函数的形状
plt.plot(x,y)
plt.show()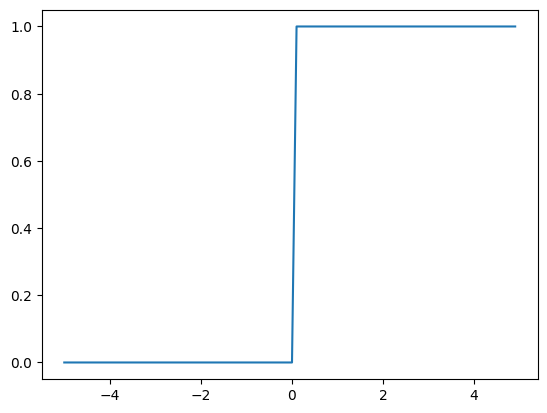
然后就是sigmoid函数的实现,也就是非平滑激活函数的实现:


sigmoid函数本质上也是一种算子(单一标量操作),所以同样是可以广播机制的;
python
import numpy as np
# 算子可以被广播,所以不用担心是单值信号的输入还是数组信号的输入
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-5.0,5.0,0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.show()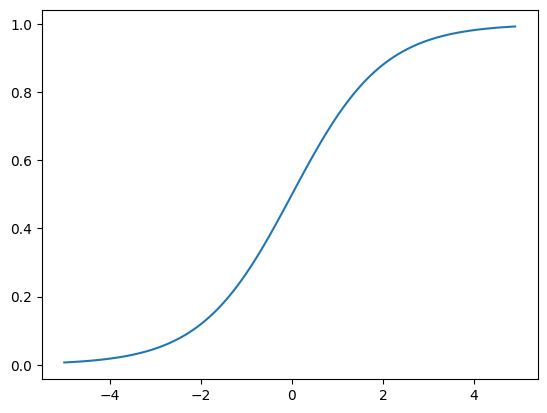

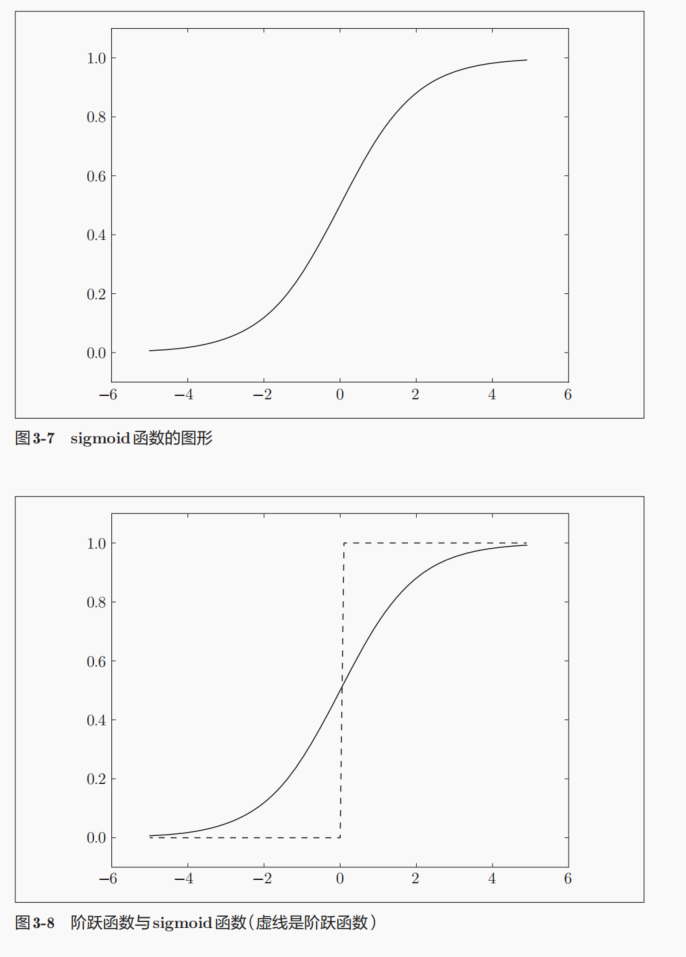

然后就是激活函数的线性(可加性,标量数乘性)与非线性:

激活函数必须是非线性函数:

ReLU函数:线性整流元

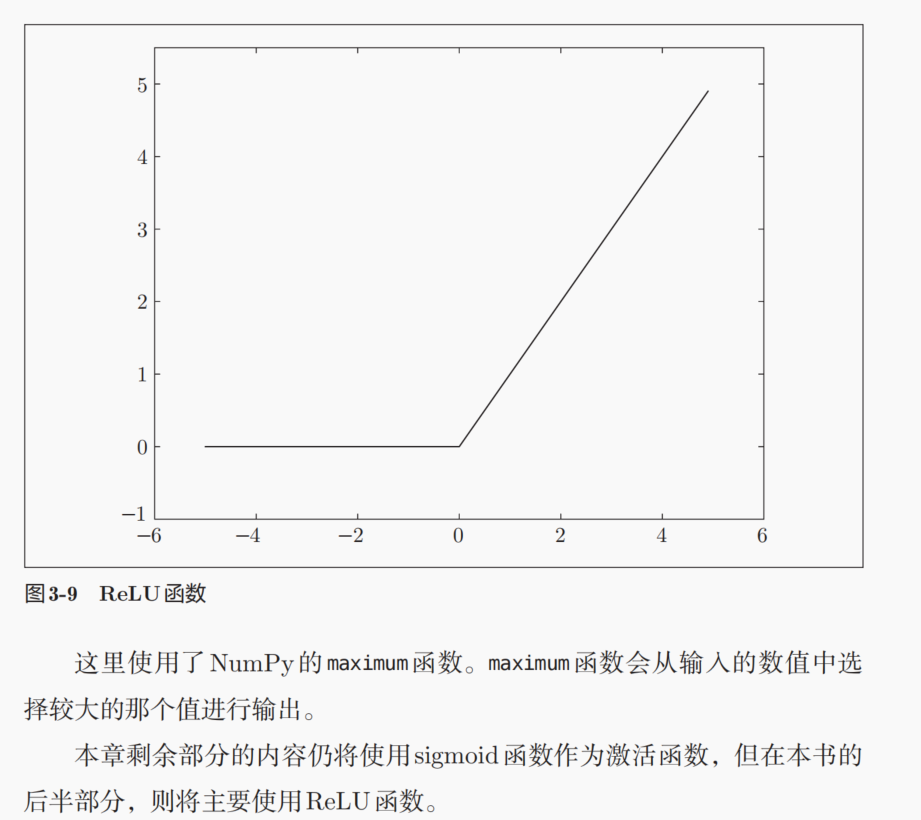
4,多维数组的运算(重点是广播机制)

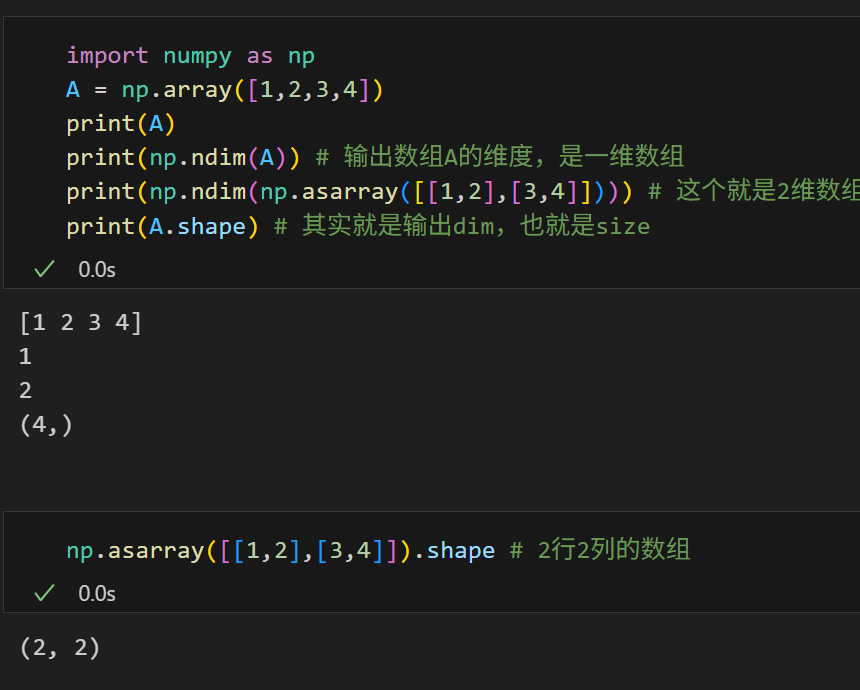
当然,这里其实也有细节需要注意,比如说(4, 1)和(4,)
(4, 1)和(4,)的区别
这两个之间有什么区别呢?
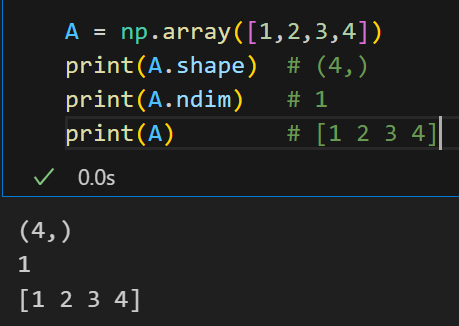
实际上上面的A是一个一维数组,这是毋庸置疑的,所以输出shape的时候是(4,),这其实是一个行向量或者是列向量的表示方式;
我们真正要看的(4,1)其实是一个二维数组,
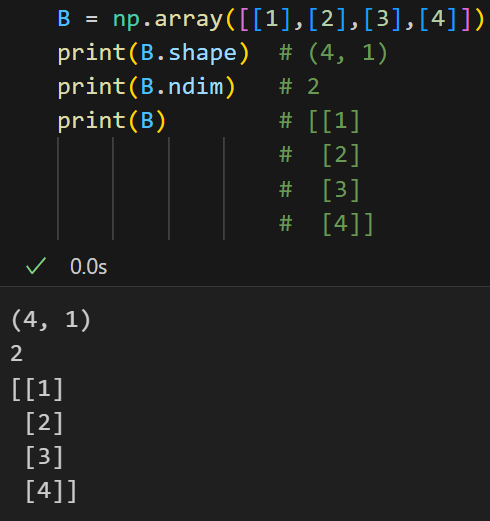
总而言之:
(4,) - 一维数组
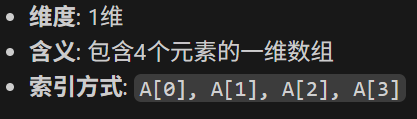
(4,1) - 二维数组(列向量)
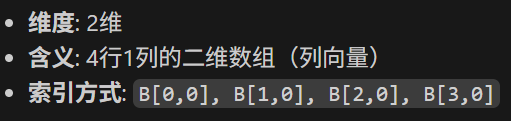
更多的区别在于:
python
# 1. 数据结构不同
import numpy as np
# 一维数组
A = np.array([1,2,3,4])
print(f"A的形状: {A.shape}") # (4,)
print(f"A的维度: {A.ndim}") # 1
# 二维数组(列向量)
B = A.reshape(4,1)
print(f"B的形状: {B.shape}") # (4, 1)
print(f"B的维度: {B.ndim}") # 2
plain
# 2. 矩阵运算行为不同
# 转置操作
print(f"A为{A},形状{A.shape},维度{A.ndim}\n")
# (4,) - 一维数组转置还是自己
print(f"A的转置为{A.T},形状为{A.T.shape},维度为{A.T.ndim}\n")
# 对应2维数组的B
print(f"B为{B},形状{B.shape},维度{B.ndim}\n")
# (1, 4) - 变成行向量
print(f"B的转置为{B.T},形状为{B.T.shape},维度为{B.T.ndim}\n")
# 转置通常与矩阵乘法相关联,什么时候需要转置呢?只有当维度不匹配的时候!
# 矩阵乘法
C = np.array([[1,2,3,4]]) # (1, 4) 行向量
print(f"C为{C},形状{C.shape},维度{C.ndim}\n")
print(f"C的转置为{C.T},形状为{C.T.shape},维度为{C.T.ndim}\n") # (4, 1) 列向量
print(f"A与C相乘:")
try:
result = A @ C.T # 一维数组可以灵活参与运算
print(f"A @ C.T结果为{result}, 形状为{result.shape}, 维度为{result.ndim}\n")
except:
print("A @ C.T运算失败\n")
try:
result = A @ C
print(f"A @ C结果为{result}, 形状为{result.shape}, 维度为{result.ndim}\n")
except:
print("A @ C运算失败\n")
print(f"B与C相乘:")
result = B @ C # 严格的矩阵乘法 (4,1) × (1,4) = (4,4)
print(f"结果为{result}, 形状为{result.shape}, 维度为{result.ndim}\n") # (4, 4)
主要是这里的一维数组参与运算时候的转变,
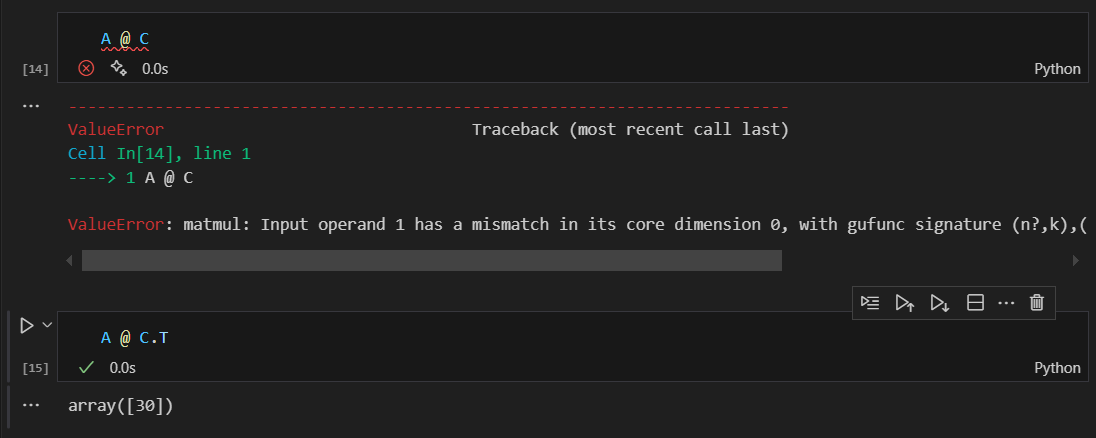
这里A是一维数组,注意numpy中一维数组和行列向量是不一样的,行列向量是二维数组!
然后这里的C是二维数组,是C为[[1 2 3 4]],形状(1, 4),维度2;
依据线性代数的简单知识,我们知道矩阵运算的时候要确定矩阵的维度是否匹配,
C我们是知道的,右乘是1行4列;
那么A呢,A在这里只是一维数组。所以numpy在运算的时候其实是自动将一维数组进行了升维。
一维数组左乘的时候作为行向量,所以这个时候A是实际上是A.reshape(1,4),变成了1行4列的行向量;
所以我们这个时候只能将C进行转置,转置为4行1列的矩阵,才能够和A.reshape(1,4)进行右乘,不然运算就会报错。


总而言之,一维数组在矩阵乘法的时候是很灵活的,可以灵活运算,
左乘被当作行向量reshape,右乘被当作列向量reshape

但是以为数组实际上有些时候在特征处理的时候并不是很方便,所以在机器学习中我们经常将一维数组转换为二维数组:通过使用reshap函数
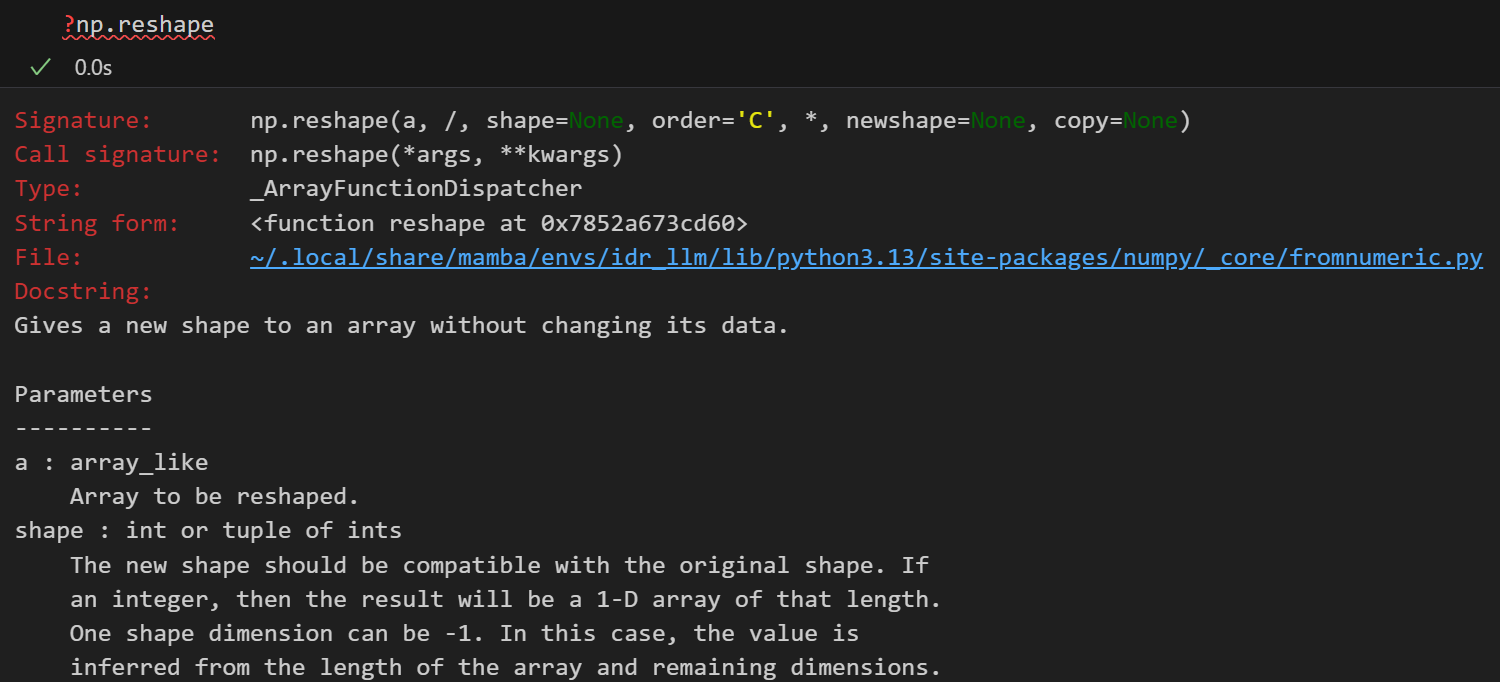
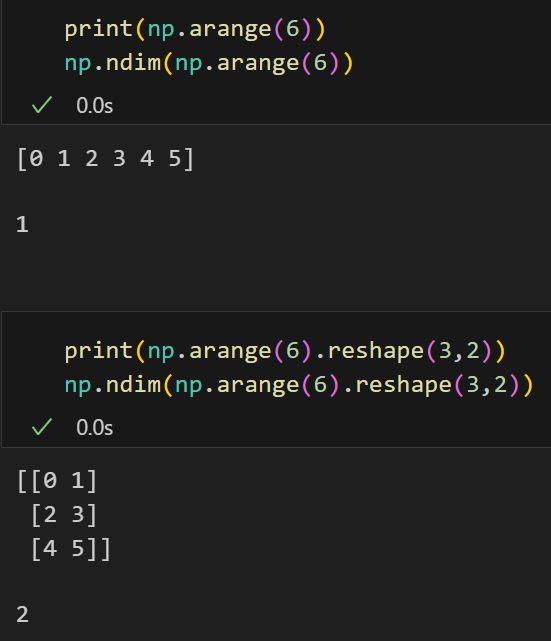
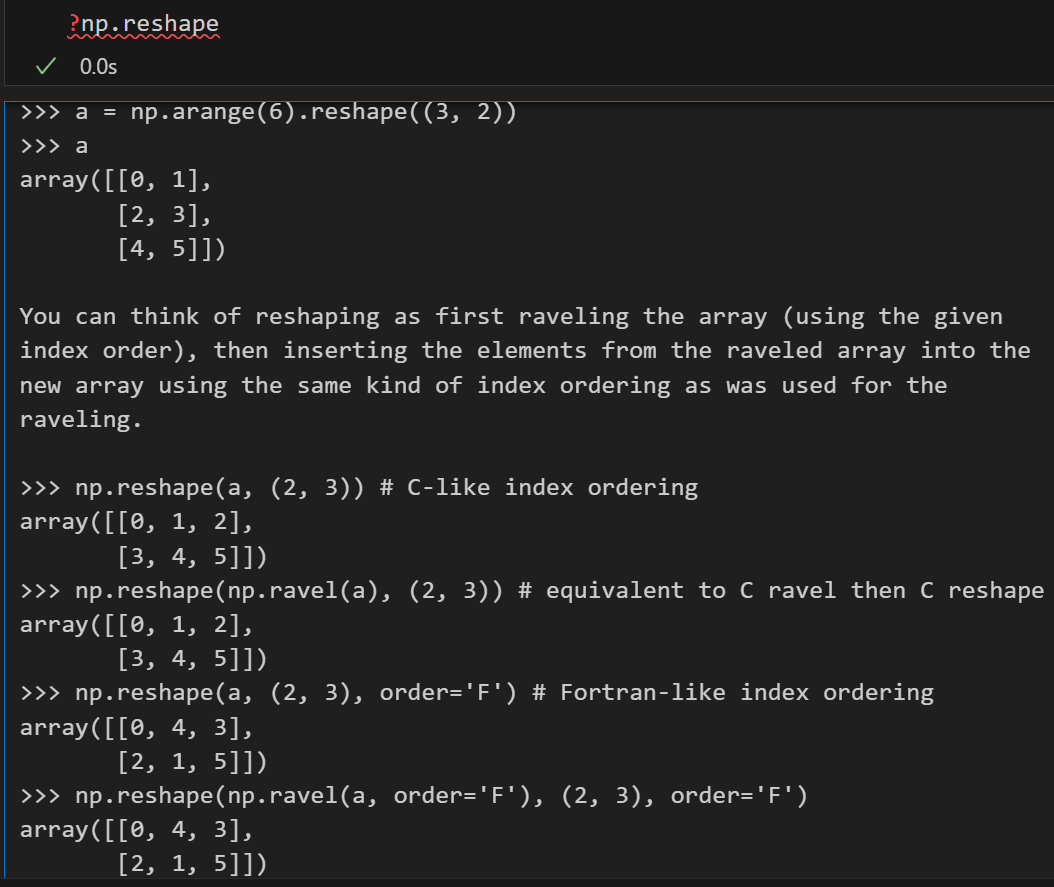
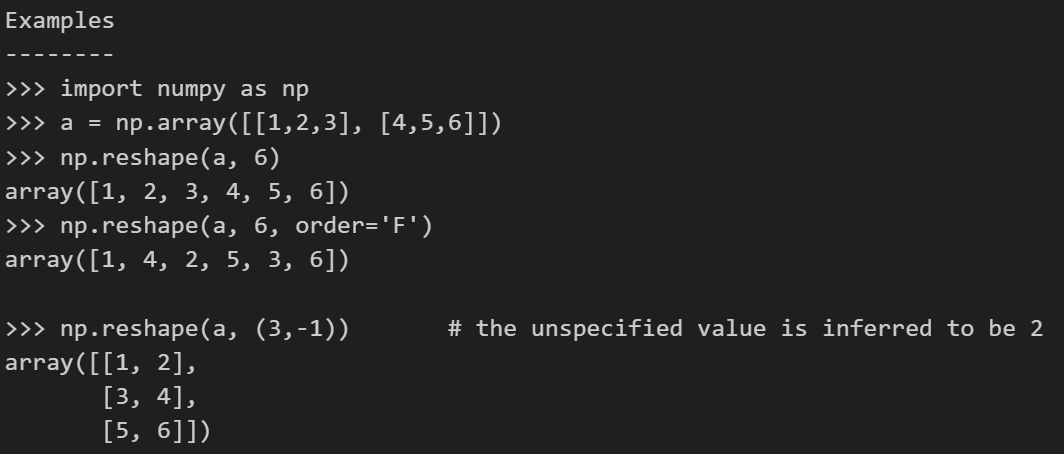
然后这里没有指定的值,其实可以使用-1来替代(一般指定-1之后,numpy会自动推断出来-1具体替代的维度)
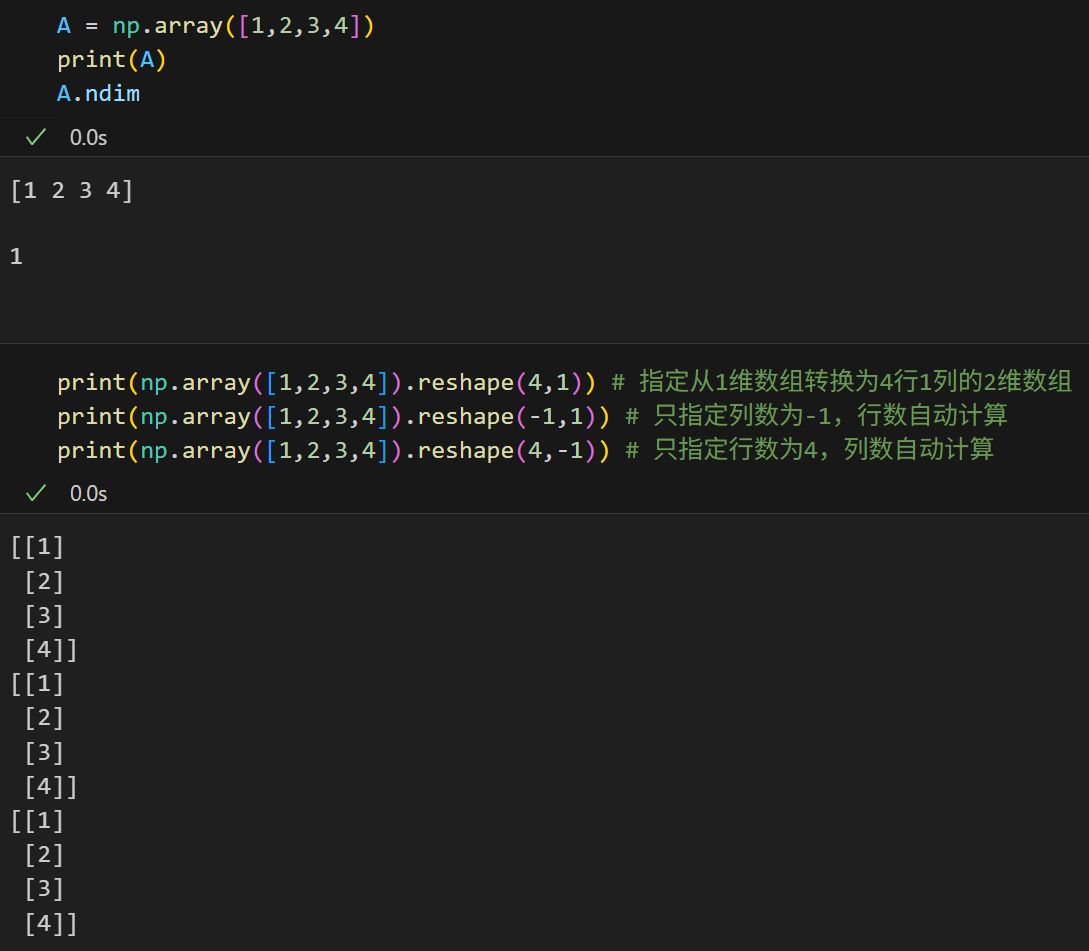

多维数组我之前关于sklearn的简单机器学习的博客系列中总结了1个口诀------"行0行,列1列",
行是第0维(从index上讲,0-indexed)------0维第一个维度有3行,3个元素;
列是第1维------1维第二个维度有2列,2个元素。
numpy中很多函数有axis这个参数,axis=0还是1,其实就是看维度,我一般按照我这里的经验进行判断。

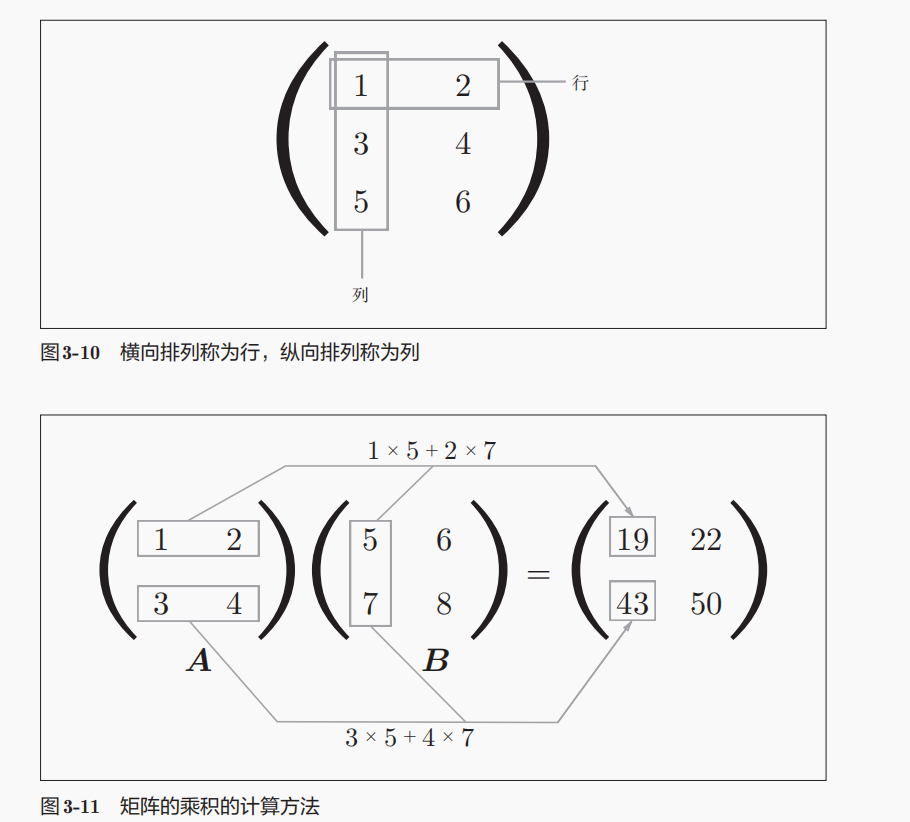




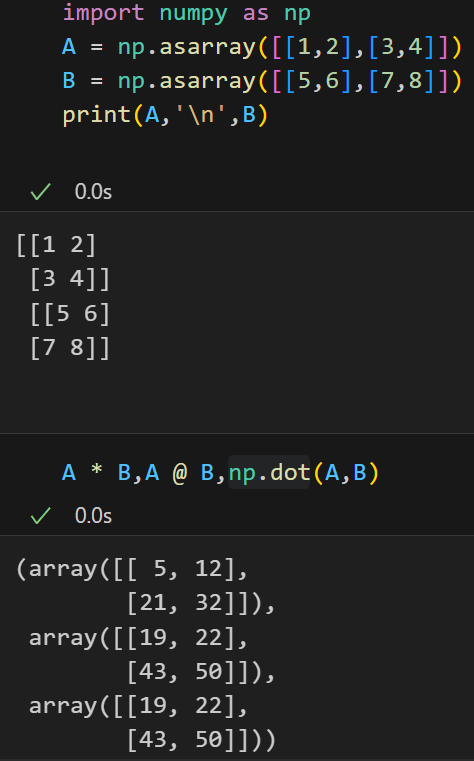
*运算是逐元素运算(element-wise),也就是矩阵A的第1行第1列和矩阵B的第1行第1列相乘,得到结果矩阵的第1行第1列元素,其余同理;
@和np.dot这里都是指的矩阵乘法,也就是点积;
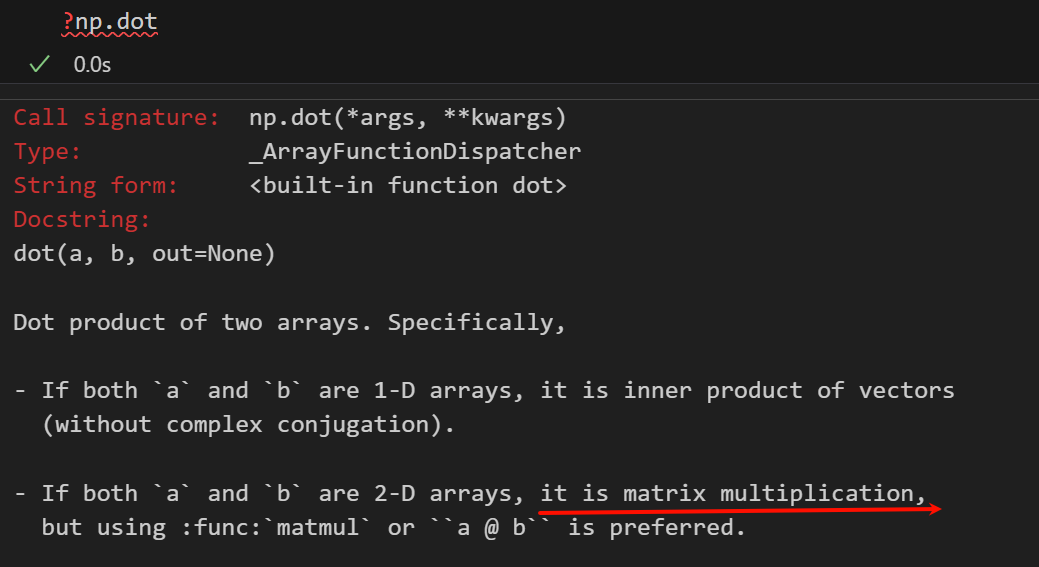
对于双2维矩阵来说,这里的点积内积其实就是矩阵乘法;
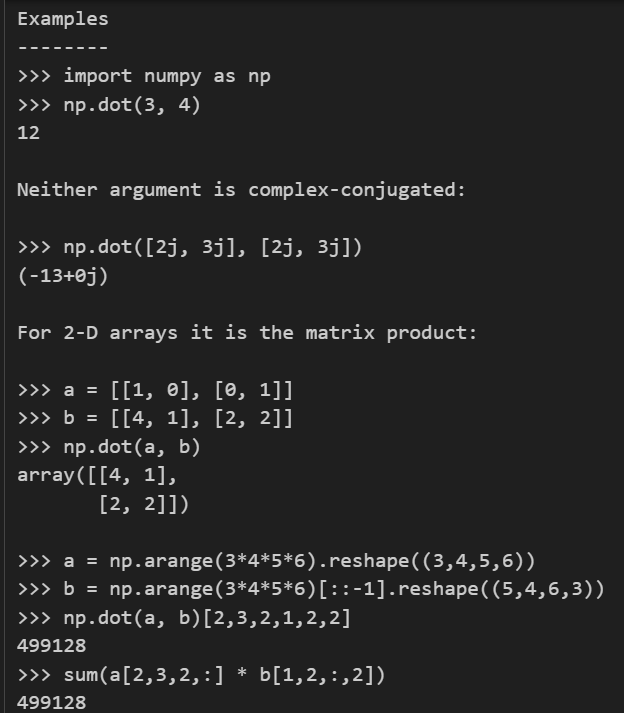

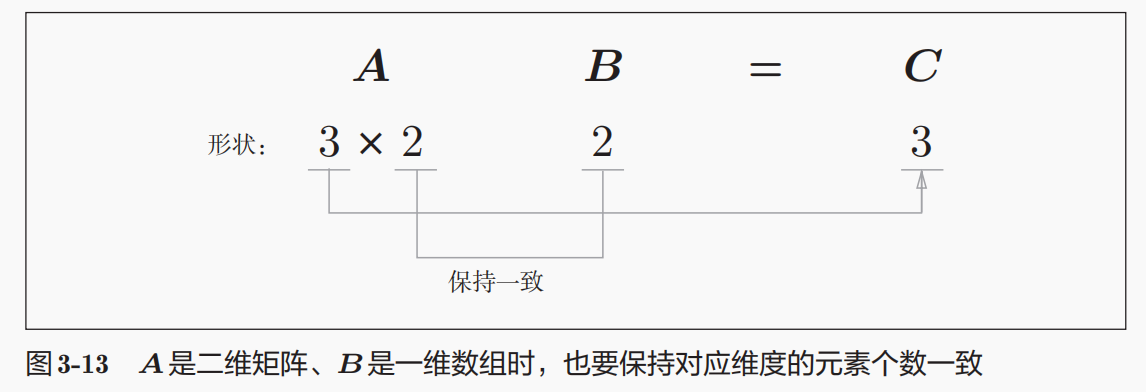
按照我们前面的说法,一维数组参与矩阵运算比较灵活,右乘的话作为列向量,所以这里其实是
A * B.reshape(2,1) ------》当然,实际结果上并不是(3,1)的列向量,
运算结果的3个数字是没有算错的,
总体逻辑还是应该按照(3,2) * (2,) = (3,)还是一维数组来考虑,
计算结果是按照(3,2) * (2,).reshape(2,1) 来计算,
总之:
**逻辑按照(3,2) * (2,) = (3,),运算按照(3,2) * (2,).reshape(2,1) **
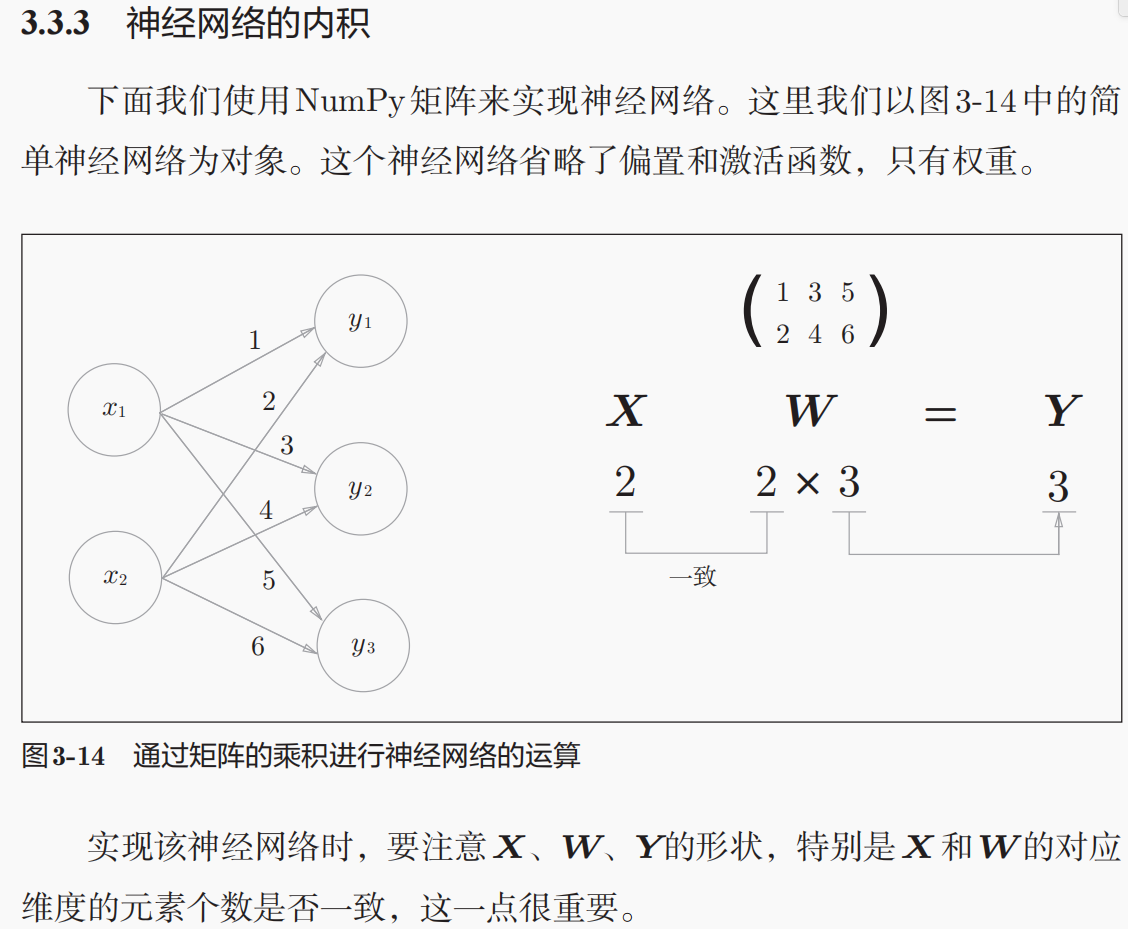
一维数组的输入,2个输入每个输入对应的3个weight,一维数组的输出


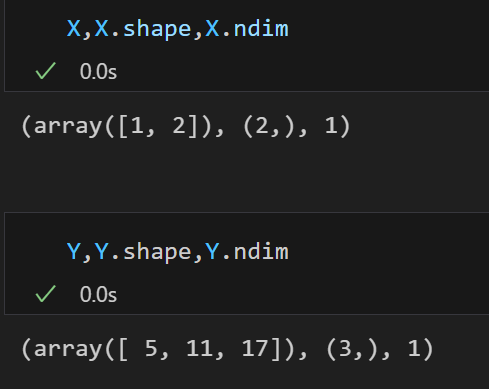
结合前面涉及到一维数组的运算,粗略总结如下:
涉及到一维数组运算的,运算逻辑按照一维数组.reshape来计算(需要匹配维度),
结果逻辑按照依然是一维数组来:
因为一维数组左乘作为行向量,当作是(1,-1自动推断);右乘作为列向量,当作是(-1自动推断,1),
其实可以看到结果无论如何,必定有一个维度是1,所以结果形式依然是一维数组

说白了,就是numpy运算的时候,自动升维是我们理解运算的逻辑;
计算结果出来之后,如果还有一个维度是1维的,自动降维是numpy自动移除了最后的单一维度。
5,神经网络实现中的矩阵运算
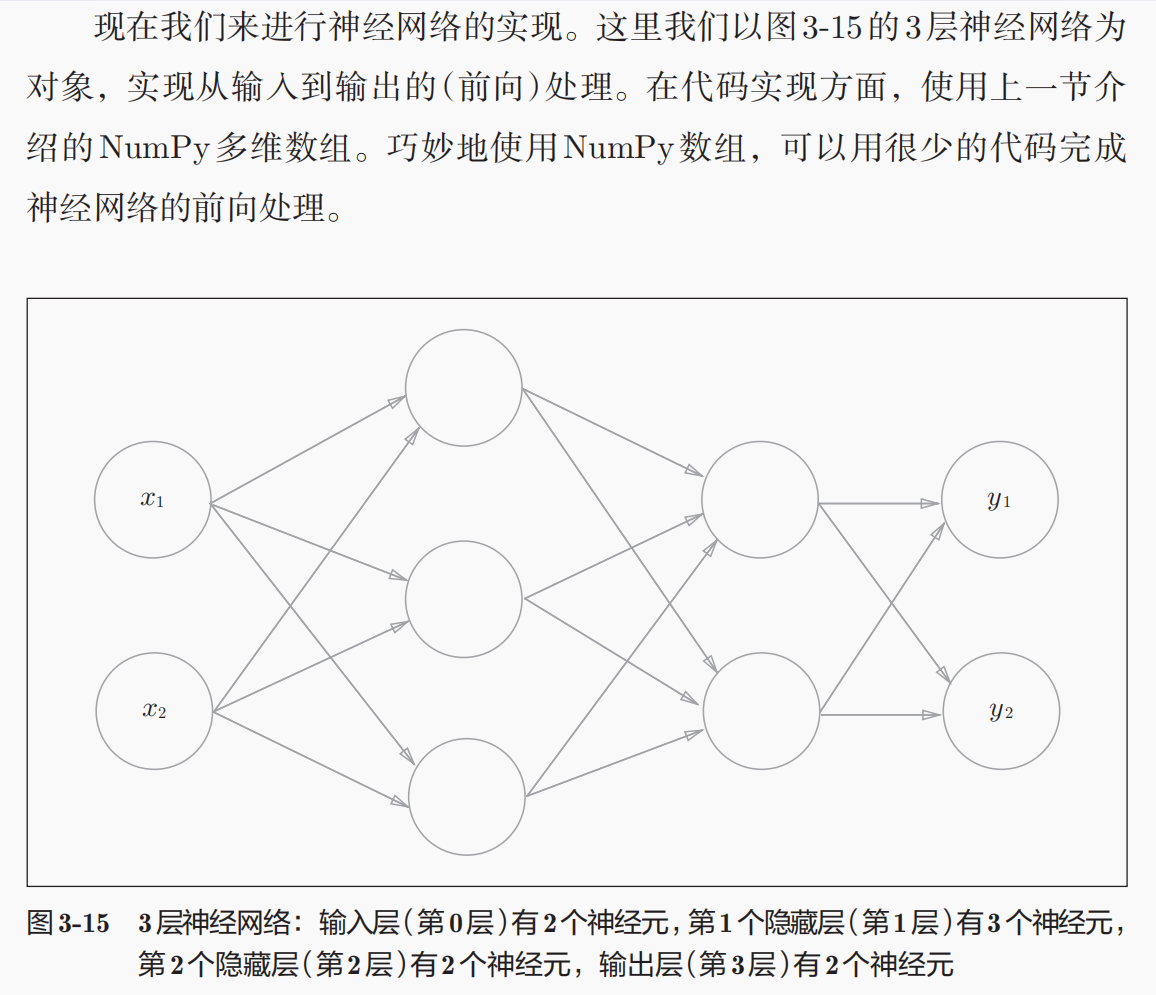

当然,符号不是关键,符号是自定义的,按照后一层前一层来标注,我猜想此处是为了照顾后面计算梯度的时候反向传播BP相协调。(从之参数理解上就认为是wij是后一层的第i个神经元接受了前面一层第j个神经元的输入)
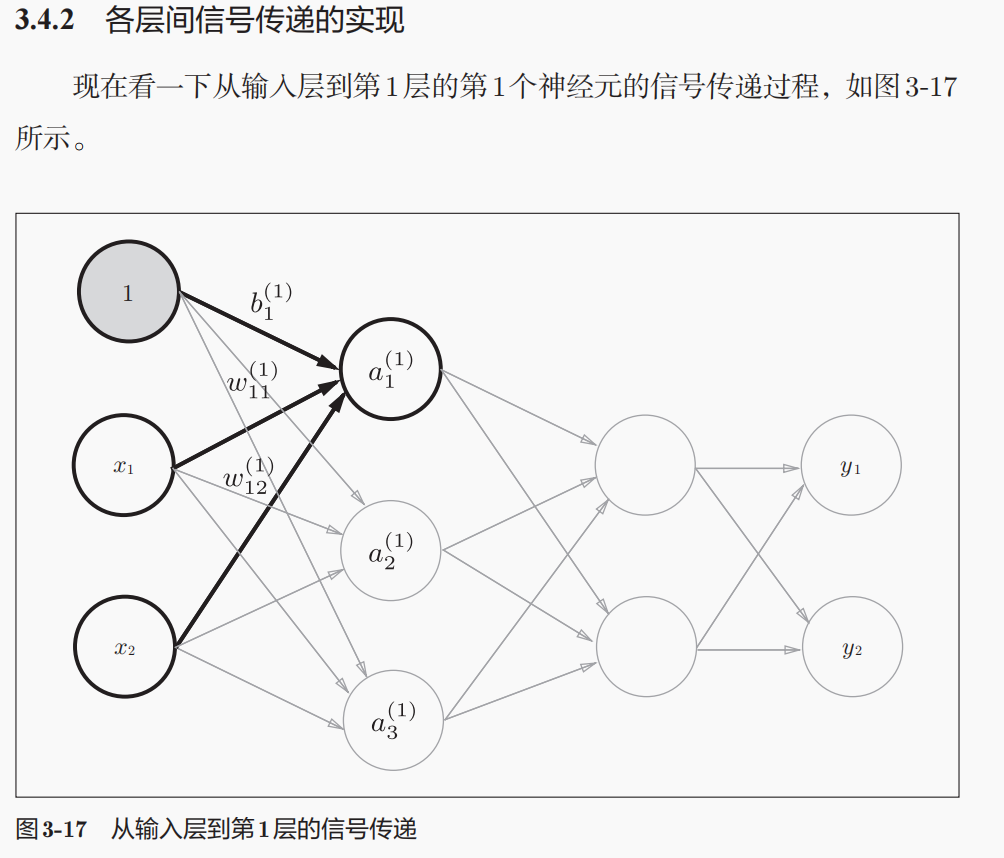



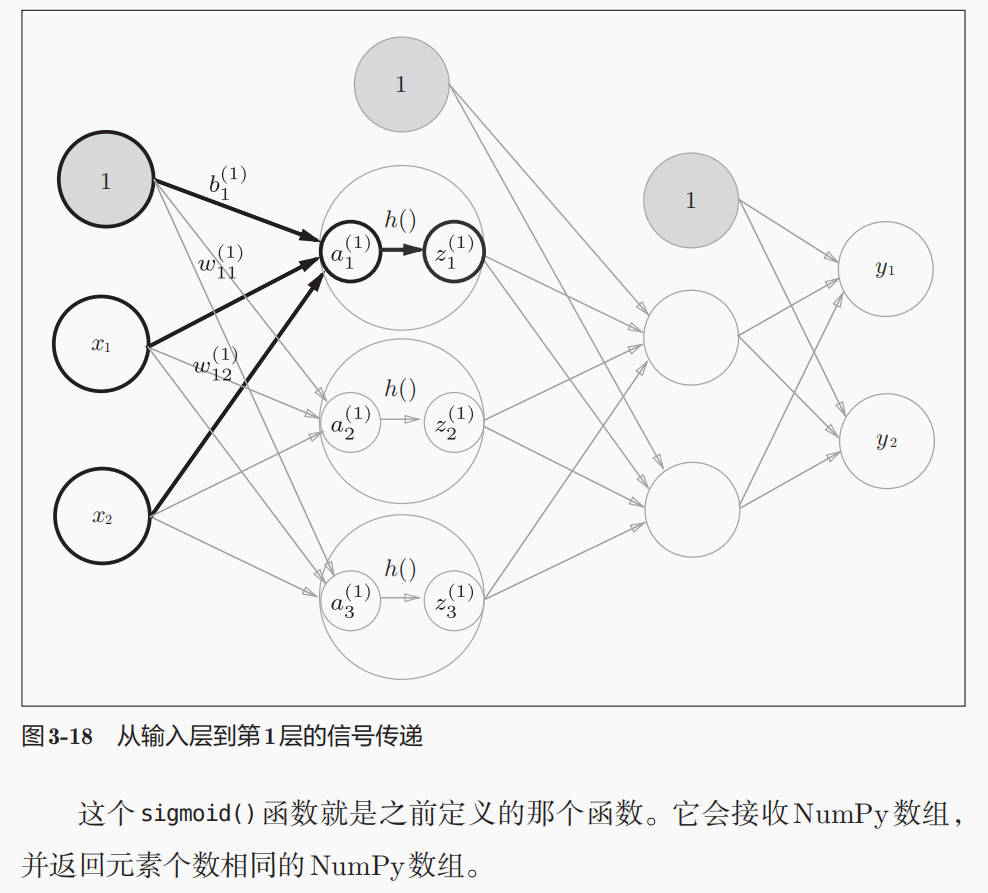

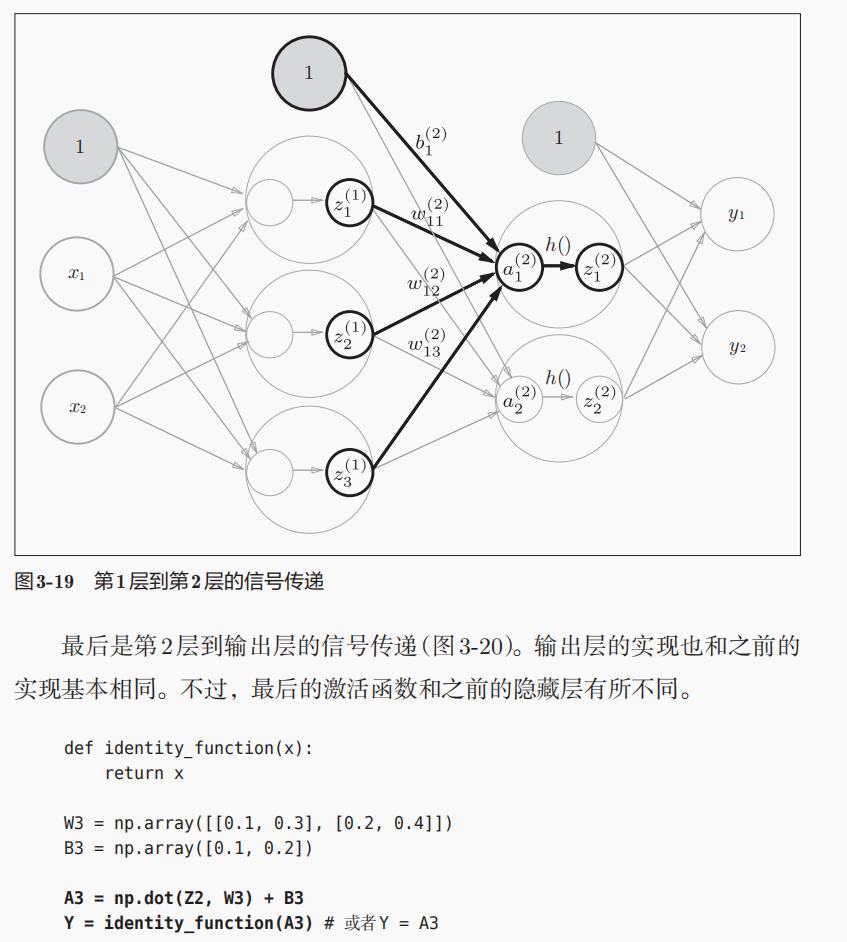

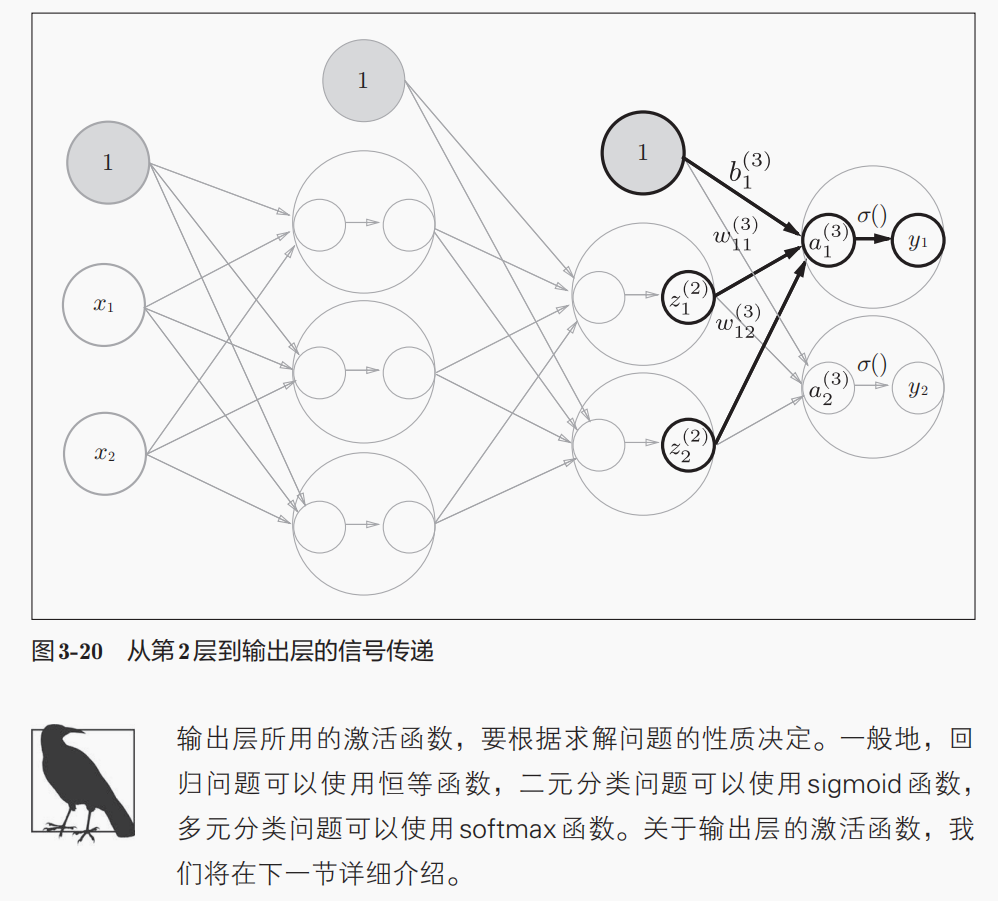
参数矩阵的维度shape
权重矩阵的维度shape:(前1层神经元的数目,后一层神经元的数目),
所以上面的w1是2行(输入层的2个神经元)3列(到第1层隐藏层的3个神经元),w2是3行2列;
偏置矩阵的维度shape:后一层神经元的数目,是1个一维数组



从第一性原理上讲,其实实现一个神经网络的第一要素我们已经很简单地完成了,
下面其实就已经是1个神经网络了!
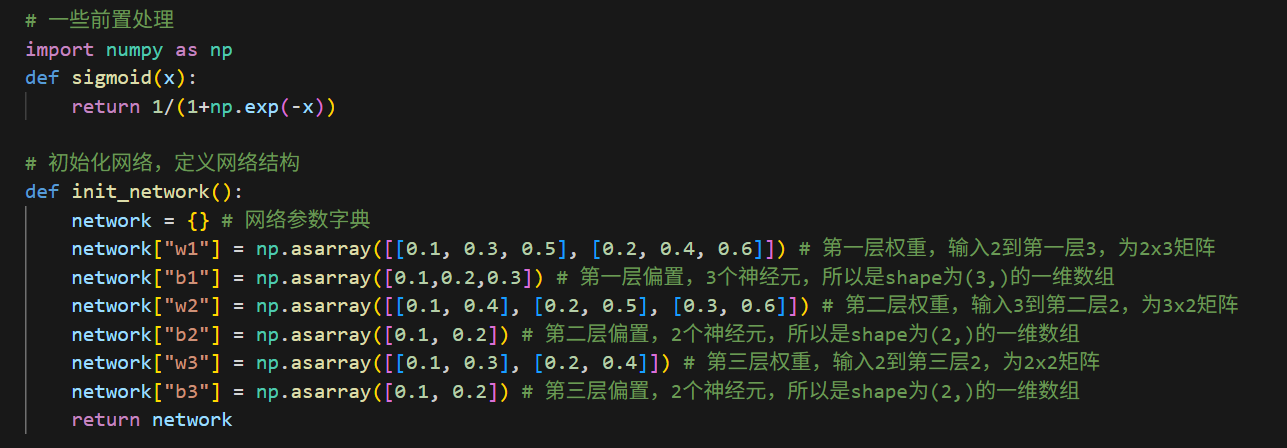

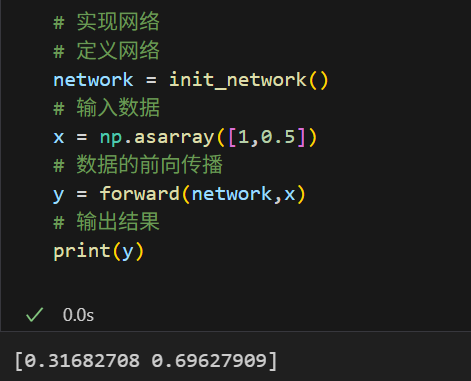
输入数据在权重左乘
在矩阵的实际运算写法上,我们一般按照顺序写成输入权重+偏执(注意是输入数据权重,不是权重*输入数据,看数学表达式中的维度匹配,数据输入写在左边)
6,输出层的设计:




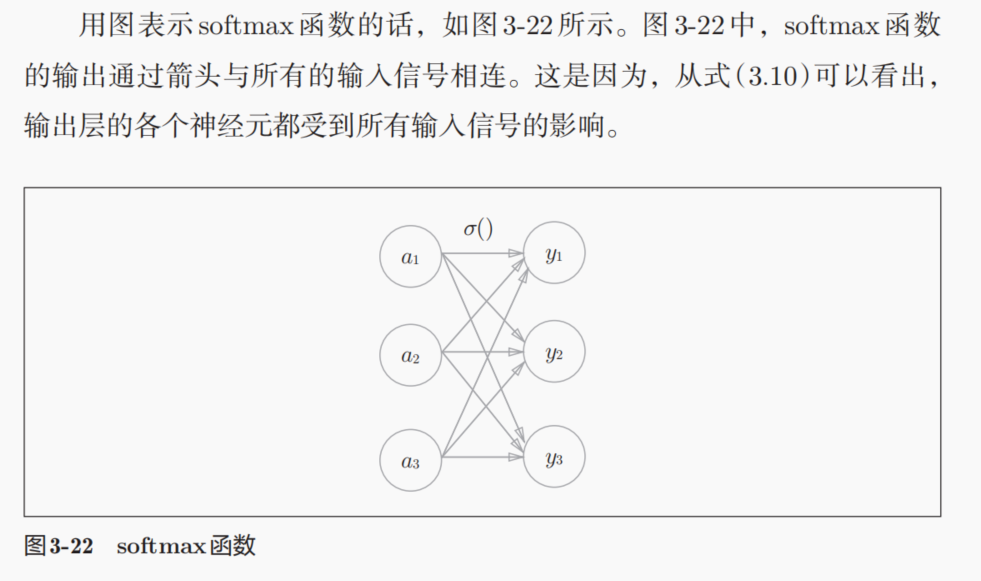

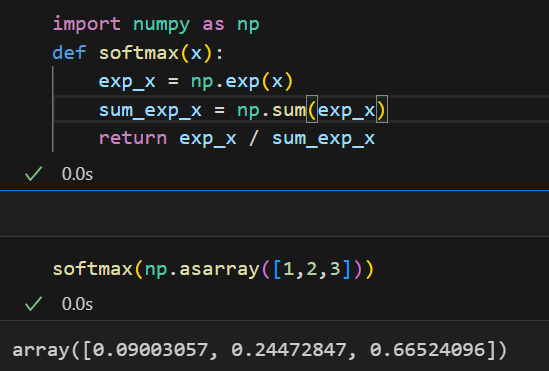


果然会有值溢出的问题:
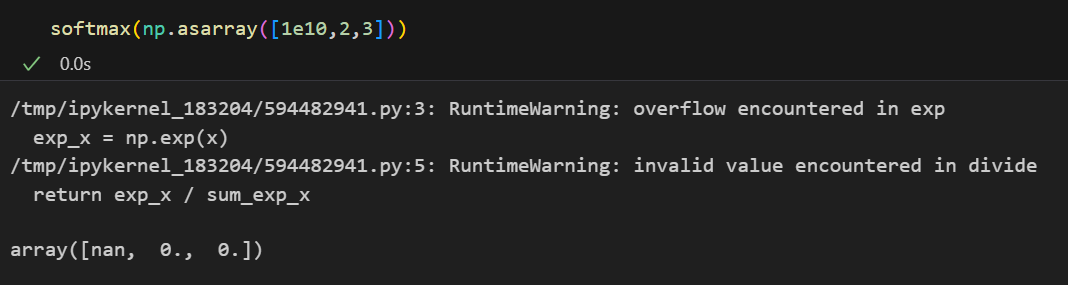
可以类似于归一化来解决溢出的最大值问题:

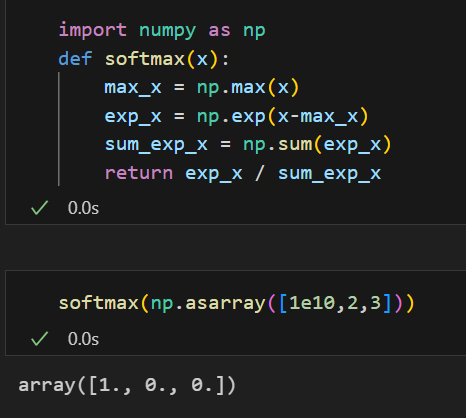



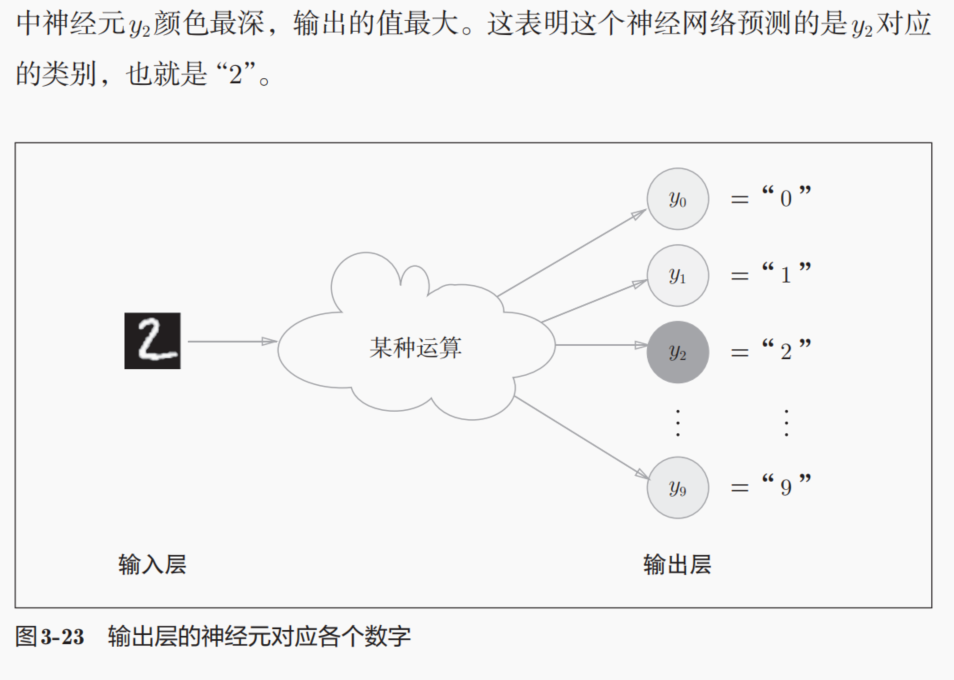
7,牛刀小试:手写数字识别

学习:训练model,计算梯度,反向传播;
推理:使用训练好的model,传递数据并计算,前向传播




但是由于mnist数据集下载一直有问题,所以代码没有复现展示,暂时搁置,如果mnist数据集有其他可以下载的方式,倒是可以以后试试(to do)!!!!!!!!
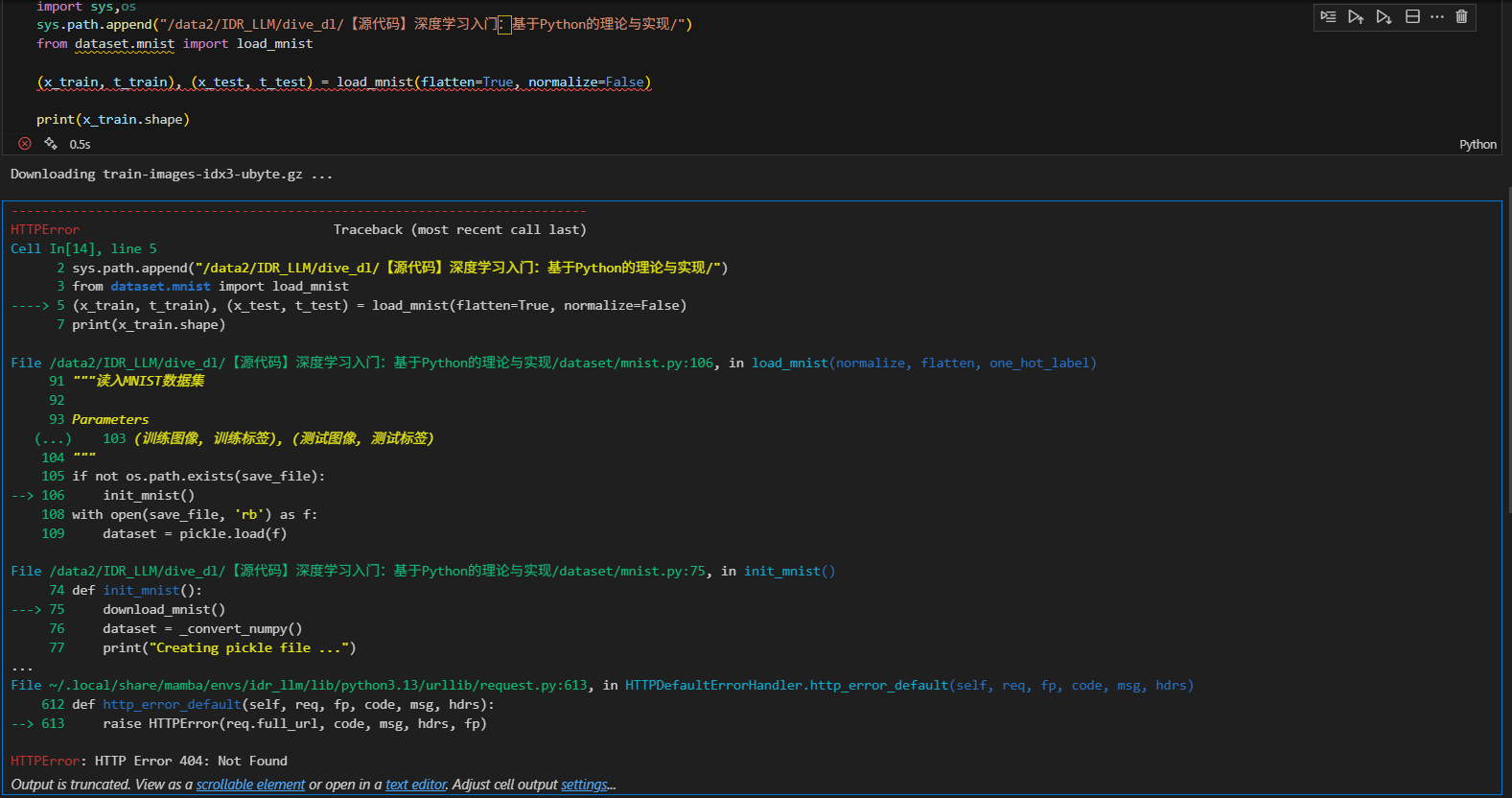



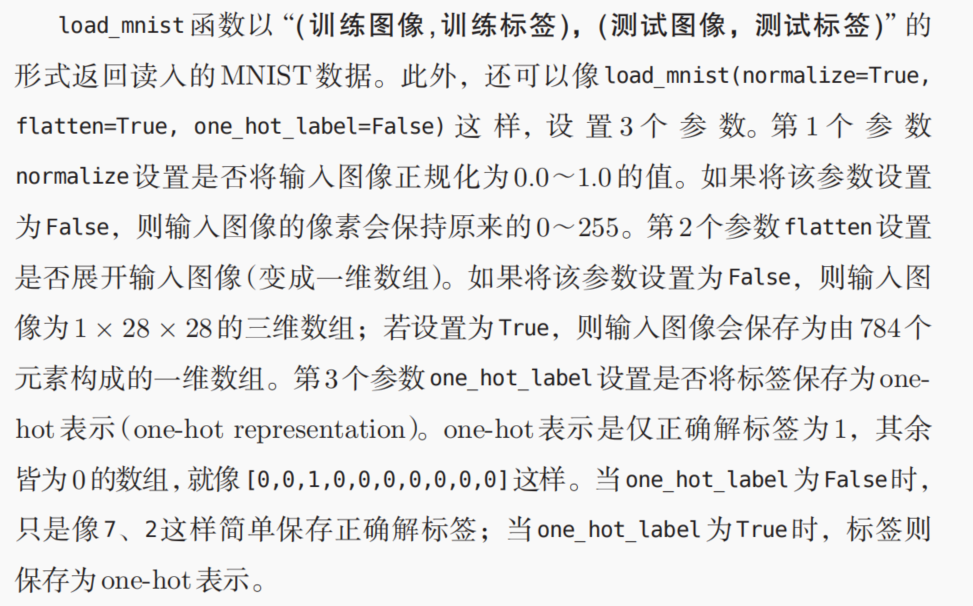
注意图像像素的flatten和reshape的复原。

因为之前我们假设学习已经完成,所以学习到的参数被保存下来。假设保存在sample_weight.pkl
文件中,在推理阶段,我们直接加载这些已经学习到的参数。




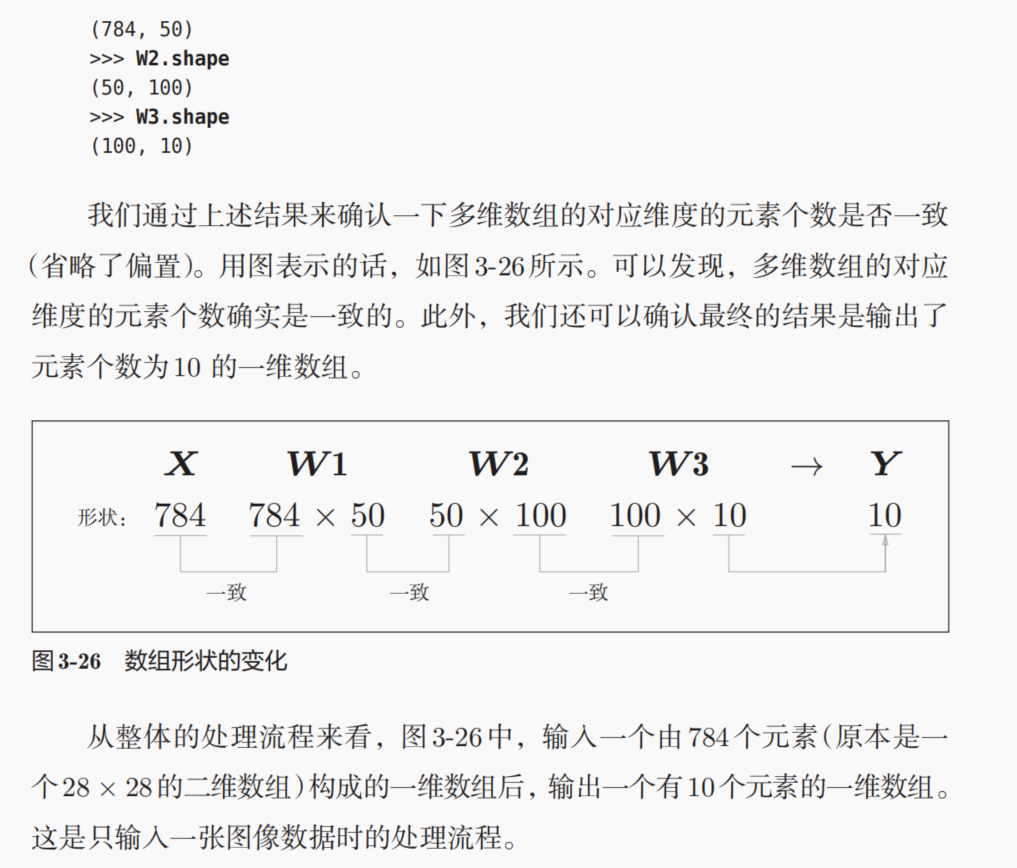
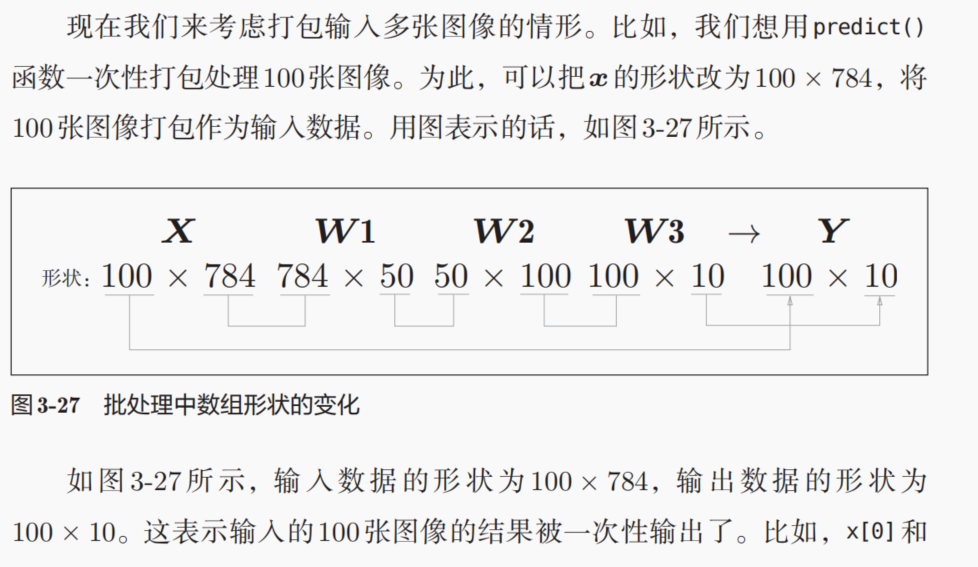




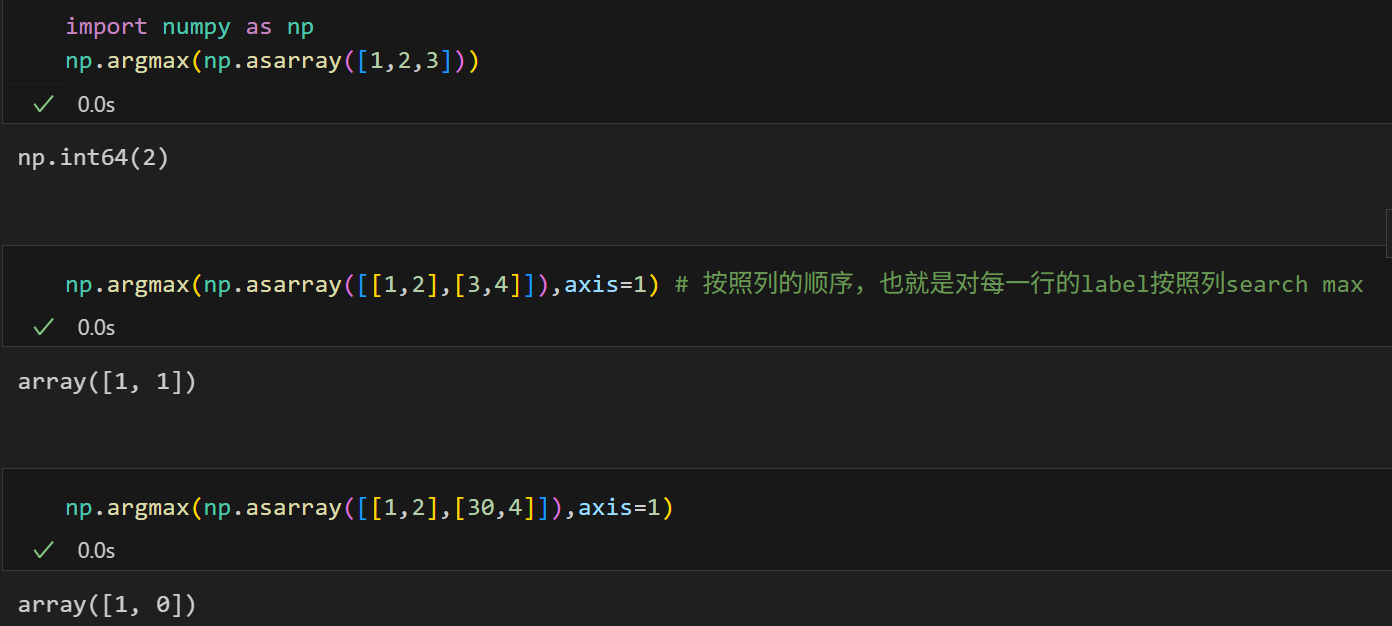
8,本章小结
