递归与迭代的优雅之舞：我在评论区功能中悟出的“树”之道（104. 二叉树的最大深度）

递归与迭代的优雅之舞：我在评论区功能中悟出的"树"之道😎

大家好，我是一个热衷于在代码世界里摸爬滚打的开发者。今天想跟大家聊聊一个我最近在项目中遇到的"小"问题，以及它如何让我对一个基础算法------"二叉树的最大深度"------有了全新的认识和感悟。

我遇到了什么问题

故事是这样的，我们团队正在开发一款新的社交应用，我负责的是其中一个核心功能：嵌套评论区。就像你在各大论坛或社交媒体上看到的那样，用户可以对一篇文章发表评论，也可以对其他人的评论进行回复，形成一个层层嵌套的评论楼。

功能初期开发很顺利，但产品经理小姐姐（PM）很快就提出了一个新的需求："为了保持UI的整洁和可读性，咱们得限制一下评论的嵌套层级，最多不能超过10层。"

我当时的第一反应是："简单！" 但下一秒，一个问题浮现在我脑海里：我怎么知道当前用户回复的评论，已经是在第几层了？ 🤔

我需要一个方法，能在用户点击"回复"时，迅速判断出当前评论节点的"深度"。更进一步说，为了做一些全局的统计和展示，我需要能随时计算出任何一个评论分支下的"最大嵌套深度"。

这个评论和回复的结构，一个父评论下有多个子回复，每个子回复又可以有自己的回复......这不就是一棵活生生的"树"嘛！而PM的需求，本质上就是要求我计算出这棵"评论树"的最大深度。

这问题一下就变得有趣起来了，因为它完美地对应上了 LeetCode 上的这道经典题目：

104. 二叉树的最大深度

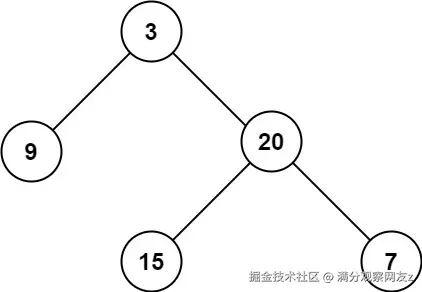
给定一个二叉树 root ，返回其最大深度。二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。

题目的提示也给了我一些信息：

树中节点的数量在 [0, 10^4] 区间内：这个数量级告诉我，一个 O(N)（N是节点数）的算法是完全可以接受的，我不需要去想什么黑科技。
-100 <= Node.val <= 100：节点的值，在我的场景里就是评论内容，跟深度计算无关。可以忽略。

那么，开干！

我是如何用[深度优先搜索(DFS)]解决的

灵光一现：递归大法好！

我盯着草稿纸上画的评论树，突然"恍然大悟"😉。

一棵树（或者一个评论分支）的最大深度是多少？

如果这个分支是空的（没有评论），那深度就是0。
如果不为空，那它的深度就是 1（它自己这一层）+ 它所有回复中，那个最深的回复分支的深度。

这简直就是为递归量身定做的！一个大问题可以分解成性质相同的小问题。我迅速写下了第一版解决方案，也就是深度优先搜索（DFS）的递归实现。

它的思路是利用递归"分而治之"的思想。一个节点的深度等于其最深的子节点深度加一。我们只需要不断地向下递归，直到遇到没有回复的"叶子评论"，然后层层返回深度即可。

java 复制代码

/*
 * 思路：递归法（深度优先搜索）。
 * 这方法太直观了！一个评论树的深度 = 1 + max(左边回复分支的深度, 右边回复分支的深度)。
 * 时间复杂度：O(N)，每个评论节点我们都得看一遍。
 * 空间复杂度：O(H)，H是评论树的高度。最坏情况是用户恶意盖楼，一条线回到底，那就是O(N)。
 */
class Solution {
    public int maxDepth(TreeNode root) {
        // 如果根节点（顶层评论）为空，那深度自然是0。
        if (root == null) {
            return 0;
        }

        // 递归去问问左边的回复分支有多深。
        int leftDepth = maxDepth(root.left);
        // 再问问右边的回复分支有多深。
        int rightDepth = maxDepth(root.right);

        // Math.max() 是Java里最直接的比较大小的工具，清晰明了。
        // 我的深度就是我所有回复里最深的那个，再加我自己这一层。
        return Math.max(leftDepth, rightDepth) + 1;
    }
}

这代码简洁、优雅，完美地解决了问题。我甚至已经能想象到PM小姐姐满意的微笑了。

踩坑与反思：万一有人恶意盖楼怎么办？

但作为一个严谨的程序员，我多想了一步。如果有个无聊的用户，在一个评论下疯狂地自我回复，盖了一个上万层的"摩天高楼"呢？

我的递归代码，每调用一次 maxDepth，就会在程序的"调用栈"上增加一层。如果这个栈太深，就会导致一个经典的错误：StackOverflowError！栈被撑爆了！💥

虽然题目提示节点数最多10^4，一般系统栈都能应付，但在实际生产环境中，我们必须考虑这种极限情况。我不能让一个恶意用户搞垮我的服务。

那么，有没有不依赖系统调用栈的方法呢？当然有！

换个姿势再来一次：广度优先搜索 (BFS)

我想，既然一条道走到黑（DFS）有风险，那我何不"广撒网"呢？我可以一层一层地来遍历我的评论树。这思路就是广度优先搜索（BFS），也叫层序遍历。

它的核心思路是使用一个队列（Queue）来辅助。首先，先把顶层评论（根节点）放进队列。接着，只要队列里还有评论，我就开始处理"一层"：先记录当前层的评论数，然后把这些评论一个个取出来，并把它们的直接回复加入队尾。每处理完一整层，深度计数器就加1。当队列为空时，所有评论都看完了，计数器的值就是最大深度。

java 复制代码

import java.util.LinkedList;
import java.util.Queue;

/*
 * 思路：迭代法（广度优先搜索/层序遍历）。
 * 一层一层地数，数到最后一层，总共数了多少次就是深度。非常稳健！
 * 时间复杂度：O(N)，每个评论还是只访问一次。
 * 空间复杂度：O(W)，W是评论树的最大宽度。如果一个热门评论有成千上万条直接回复，这里会耗费较多内存。
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
      
        // Java中 Queue 是个接口，LinkedList 实现了它，提供了经典的 offer(入队) 和 poll(出队) 操作。
        // ArrayDeque 通常性能更好，但这里用 LinkedList 完全没问题，也更经典。
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
      
        int depth = 0;
      
        while (!queue.isEmpty()) {
            // 关键一步：在开始处理新一层前，锁定当前层有多少个节点。
            int levelSize = queue.size();
          
            // 遍历处理当前层的所有节点
            for (int i = 0; i < levelSize; i++) {
                TreeNode currentNode = queue.poll(); // 从队首取出
              
                // 把下一层的节点（回复）加入队尾
                if (currentNode.left != null) {
                    queue.offer(currentNode.left);
                }
                if (currentNode.right != null) {
                    queue.offer(currentNode.right);
                }
            }
            // 处理完一整层，深度加1
            depth++;
        }
      
        return depth;
    }
}

这个方法完美地避开了栈溢出的风险，因为它用的是堆内存里的队列，空间大得多。而且逻辑清晰，一层一层数，绝对不会错。

究极进化：手动栈实现的深度优先搜索

我还想，我真的很喜欢递归那种"一条道走到黑"的逻辑，能不能在避免栈溢出的同时，保留DFS的灵魂呢？

答案是肯定的！我们可以手动模拟递归。递归用的是系统栈，那我们自己 new 一个栈（Stack）不就行了！为了实现这个，我们需要一个栈来存放待访问的节点，但只存节点还不够，我还需要知道这个节点在第几层。所以，我需要两个栈，一个存节点，一个存对应的深度。或者用一个栈存一个包含节点和深度的自定义对象。

java 复制代码

import java.util.ArrayDeque;
import java.util.Deque;

/*
 * 思路：迭代法（深度优先搜索）。
 * 模拟递归的过程，自己管理一个栈，这样多深都不怕栈溢出了。
 * 时间复杂度：O(N)，还是每个节点访问一次。
 * 空间复杂度：O(H)，和递归一样，栈的大小取决于树的高度。
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
      
        // Java官方推荐用 Deque (比如ArrayDeque) 来作为栈使用，比古老的 Stack 类性能好。
        // push 压入，pop 弹出，完美符合栈的 LIFO (后进先出) 特性。
        Deque<TreeNode> nodeStack = new ArrayDeque<>();
        Deque<Integer> depthStack = new ArrayDeque<>();
      
        nodeStack.push(root);
        depthStack.push(1);
      
        int maxDepth = 0;
      
        while (!nodeStack.isEmpty()) {
            TreeNode currentNode = nodeStack.pop();
            int currentDepth = depthStack.pop();
          
            maxDepth = Math.max(maxDepth, currentDepth);
          
            // 先把右回复压栈，再压左回复
            // 这样弹出的时候，就会先处理左回复，符合常规的DFS顺序
            if (currentNode.right != null) {
                nodeStack.push(currentNode.right);
                depthStack.push(currentDepth + 1);
            }
            if (currentNode.left != null) {
                nodeStack.push(currentNode.left);
                depthStack.push(currentDepth + 1);
            }
        }
        return maxDepth;
    }
}

这第三种方法，既有DFS的遍历逻辑，又像BFS一样健壮，不会有栈溢出的风险，可以说是集前两者优点于一身（除了代码稍微复杂一点点）。

举一反三：这些场景你也能用上！

搞定了评论区的问题后，我发现"计算树的深度"这个技能点在很多地方都用得上：

文件系统：计算一个文件夹下最深的子文件（或文件夹）路径有多长。
UI渲染：在React或Vue中，组件构成了一个组件树。分析组件树的最大深度可以帮助调试性能问题。
组织架构图：计算一个公司最大的管理层级是多少。
依赖解析 ：像npm或Maven这样的包管理器，在解析项目依赖时会形成一个依赖树，计算其深度可以分析依赖链的复杂度。

你看，一个简单的算法题，背后却关联着这么多实际的工程问题。

练练手，更熟练

如果你也对树的遍历产生了兴趣，不妨试试下面这几道 LeetCode 上的"亲戚"题目，它们会让你对DFS和BFS的理解更上一层楼：

111. 二叉树的最小深度：和最大深度是兄弟问题，但有个小陷阱哦😉。
559. N 叉树的最大深度：从"二叉"到"N叉"，思路一样，代码稍作修改即可。
102. 二叉树的层序遍历：就是我们解法二BFS的核心思想。
110. 平衡二叉树：判断一棵树是否"平衡"，就需要反复计算左右子树的深度。

希望我的这次经历能对你有所启发。下次当你再遇到看似复杂的问题时，不妨退后一步，看看它的核心数据结构是什么，或许一个经典的算法就能帮你轻松搞定！😎