深度学习之神经网络（二）

文章目录

深度学习之神经网络（二）
一、pandas是什么？
[神经网络基础：从生物神经元到 PyTorch 全连接网络](#神经网络基础：从生物神经元到 PyTorch 全连接网络)
- [1. 生物神经元 vs 人工神经元](#1. 生物神经元 vs 人工神经元)
- [2. 从单个神经元到多层网络](#2. 从单个神经元到多层网络)
- - [2.1 三层标准结构](#2.1 三层标准结构)
  - [2.2 张量视角的前向计算](#2.2 张量视角的前向计算)
- [3. PyTorch 组件精讲](#3. PyTorch 组件精讲)
- - [3.1 线性层 `nn.Linear`](#3.1 线性层 nn.Linear)
  - [3.2 激活函数](#3.2 激活函数)
  - [3.3 损失函数](#3.3 损失函数)
  - [3.4 优化器](#3.4 优化器)
- [4. 完整示例：搭建并训练 3 层全连接网络](#4. 完整示例：搭建并训练 3 层全连接网络)
- [5. 常见问题 & 提示](#5. 常见问题 & 提示)
- [6. 参考链接](#6. 参考链接)

一、pandas是什么？

神经网络基础：从生物神经元到 PyTorch 全连接网络

这篇文章把「什么是神经网络」拆成四部分：

生物原型 → 2. 数学公式 → 3. 网络结构 → 4. PyTorch 实战。
读完即可自己搭一个可训练的全连接网络。

1. 生物神经元 vs 人工神经元

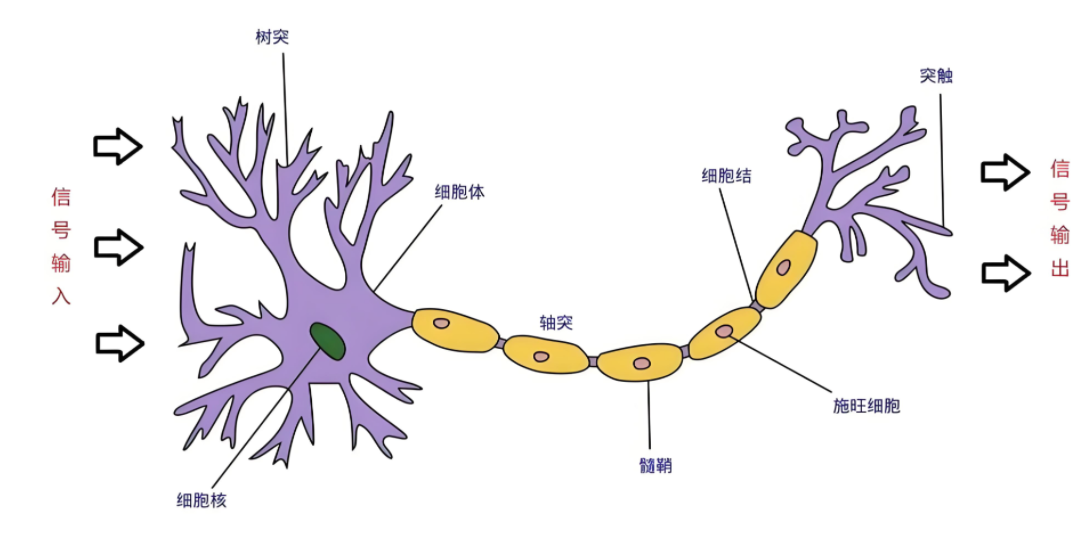
生物术语	功能	人工神经元对应
树突	接收信号	输入向量 x = $x₁, x₂, ..., xₙ$
细胞核	整合并判断是否触发	加权和 z = Σ wᵢxᵢ + b，然后通过激活函数 σ
轴突	输出信号	输出 y = σ(z)
突触	调节信号强度	权重 wᵢ 和偏置 b（可学习）

激活函数 σ 带来非线性，典型选择：

ReLU：max(0, z)
Sigmoid：1/(1+e^(−z))
Tanh：(e^z − e^(−z))/(e^z + e^(−z))

2. 从单个神经元到多层网络

2.1 三层标准结构

输入层：仅传递数据，不做计算
隐藏层：1 层或多层，每层含若干神经元，负责特征提取
输出层：产生最终预测（1 个神经元做回归，N 个做 N 类分类）

层与层之间 全连接 （Fully Connected）：上一层的每个神经元都与下一层的每个神经元相连，权重矩阵形状为 (out_features, in_features)。

2.2 张量视角的前向计算

设一批样本 x 形状 (batch, in_features) ，权重 W 形状 (out_features, in_features) ，偏置 b 形状 (out_features,)，则

复制代码

z = x @ W.T + b        # 线性部分
y = σ(z)               # 激活后输出

3. PyTorch 组件精讲

所有层、激活、损失、优化器都已在 torch.nn / torch.optim 中封装好，直接调用即可。

3.1 线性层 `nn.Linear`

python 复制代码

torch.nn.Linear(in_features, out_features, bias=True)

in_features：输入特征维度
out_features：输出特征维度
bias：是否加偏置（默认 True）

3.2 激活函数

名称	类/函数	用法示例	适用场景
ReLU	`nn.ReLU()`	`nn.Sequential(nn.Linear(64,32), nn.ReLU())`	通用默认
LeakyReLU	`nn.LeakyReLU(0.1)`	负半轴保留小梯度	GAN、避免神经元死亡
Sigmoid	`nn.Sigmoid()`	二分类输出层
Softmax	`nn.Softmax(dim=1)`	多分类输出层

3.3 损失函数

任务	推荐 API	输入要求
回归	`nn.MSELoss()`	预测/目标同形状
回归 (对异常值鲁棒)	`nn.L1Loss()`
二分类	`nn.BCEWithLogitsLoss()`	网络不需加 `Sigmoid`
多分类	`nn.CrossEntropyLoss()`	网络不需加 `Softmax`，目标为类别索引

示例：

python 复制代码

criterion = nn.CrossEntropyLoss()
loss = criterion(logits, target)   # logits: [B, C], target: [B]

3.4 优化器

python 复制代码

torch.optim.SGD(params, lr=0.01, momentum=0.9, weight_decay=1e-4)
torch.optim.Adam(params, lr=1e-3)

通用训练循环：

python 复制代码

optimizer.zero_grad()  # 清零梯度
loss.backward()        # 计算梯度
optimizer.step()       # 更新参数

4. 完整示例：搭建并训练 3 层全连接网络

以 32 维输入、单值回归为例：

python 复制代码

import torch
from torch import nn, optim

# 1. 数据（随机演示）
x = torch.randn(128, 32)
y = torch.randn(128, 1)

# 2. 模型
class MLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(32, 64),
            nn.ReLU(),
            nn.Linear(64, 32),
            nn.ReLU(),
            nn.Linear(32, 1)
        )
    def forward(self, x):
        return self.net(x)

model = MLP()

# 3. 损失与优化器
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)

# 4. 训练 100 步
for step in range(100):
    pred = model(x)
    loss = criterion(pred, y)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if step % 20 == 0:
        print(f"step {step:3d} | loss {loss.item():.4f}")

5. 常见问题 & 提示

权重太多怎么办？

全连接层参数量 = in_features × out_features + out_features，对高维输入（如图像）改用卷积层 nn.Conv2d。
ReLU 死亡神经元？

尝试 LeakyReLU、PReLU 或更好的初始化（He/Kaiming）。
过拟合？
- 加 Dropout nn.Dropout(p=0.5)
- 权重衰减 weight_decay=1e-4
- 早停、数据增强
训练不收敛？
- 确认学习率过大/过小
- 检查数据归一化
- 确认损失函数与任务匹配

6. 参考链接

PyTorch nn 文档：https://pytorch.org/docs/stable/nn.html
PyTorch optim 文档：https://pytorch.org/docs/stable/optim.html

深度学习之神经网络（二）

深度学习之神经网络（二）

文章目录

一、pandas是什么？

神经网络基础：从生物神经元到 PyTorch 全连接网络

1. 生物神经元 vs 人工神经元

2. 从单个神经元到多层网络

2.1 三层标准结构

2.2 张量视角的前向计算

3. PyTorch 组件精讲

3.1 线性层 nn.Linear

3.2 激活函数

3.3 损失函数

3.4 优化器

4. 完整示例：搭建并训练 3 层全连接网络

5. 常见问题 & 提示

6. 参考链接

3.1 线性层 `nn.Linear`