在探索现代人工智能的辉煌成就时,我们常常忽略那些奠定基石的早期思想。20 世纪中叶,当"机器学习"这一概念尚未被明确界定,工程师和数学家们已在信号处理领域悄然孕育了其核心算法。其中,自适应滤波器的发展尤为关键------它不仅解决了噪声抑制的工程难题,更意外地为后来的学习算法提供了数学框架。
这一事件的关键人物是 Bernard Widrow 和 Ted Hoff。他们在研究如何动态调整滤波器权重,优化信号输出时,提出了最小均方(LMS)算法。这一算法通过逐点计算误差迭代更新权重,构建了随机梯度下降(SGD)的雏形。更长远地看,他们的工作直接催生了第一个可训练的神经网络 ADALINE,并间接启发了反向传播算法的设计。
然而,这些早期技术突破的价值不仅在于其历史意义。从自适应滤波器的数学形式中,我们可以清晰地看到它与现代神经网络中"神经元"的共性:两者均通过权重与输入的线性组合生成输出。这说明了机器学习的本质 ------ 无论模型如何复杂,其基础仍是优化权重的过程。
理解这一起源,对今天的实践者仍有现实意义。在后续章节中,我们将从移动平均滤波器出发,逐步拆解这一思想如何演变为可训练的自适应系统,并最终与机器学习交汇。
01 基础概念:从信号处理到机器学习
信号处理与机器学习之间的桥梁建立在数学表达的共性之上。在信号处理领域,滤波器的核心任务是提取有效信号并抑制噪声干扰。其中,移动平均滤波器作为最基本的线性滤波器,通过计算信号在固定窗口内的算术平均值来实现平滑处理。这一过程的数学表达可以简洁地表示为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> y = 1 N ∑ i = 1 N x i y=\frac{1}{N}\sum_{i=1}^Nx_i </math>y=N1∑i=1Nxi
式中, <math xmlns="http://www.w3.org/1998/Math/MathML"> N N </math>N 代表窗口长度, <math xmlns="http://www.w3.org/1998/Math/MathML"> x i x_i </math>xi 为输入信号序列。值得注意的是,该表达式可以改写为向量内积形式:
<math xmlns="http://www.w3.org/1998/Math/MathML"> y = w T x y=\mathbf{w}^T\mathbf{x} </math>y=wTx
其中权重向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> w w </math>w 的所有元素均为 <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 / N 1/N </math>1/N。这种表达形式与神经网络中单个神经元的线性变换完全一致,唯一的区别在于神经网络中的权重是可训练参数而非固定值。
进一步分析可以发现,移动平均滤波器的滑动计算过程本质上是一种一维卷积运算。在信号处理术语中,这被称为"有限冲激响应"(FIR)滤波。当我们将这种固定权重的滤波器扩展为可自适应调整的形式时,就得到了自适应滤波器的基本结构。
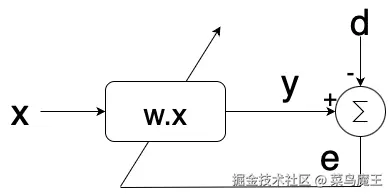
自适应滤波器的数学表达仍然保持线性组合形式:
<math xmlns="http://www.w3.org/1998/Math/MathML"> y = ∑ i = 1 N w i x i y=\sum_{i=1}^Nw_ix_i </math>y=∑i=1Nwixi
但其核心突破在于引入了权重调整机制。这种机制通过比较滤波器输出与期望信号之间的误差来动态更新权重参数。从计算角度看,这种结构已经具备了现代机器学习模型的三个基本要素:可调参数、误差评估和参数更新规则。
在信号处理向机器学习演进的过程中,最关键的理论突破是将固定权重的确定性系统转变为可训练的自适应系统。当我们将自适应滤波器的训练过程抽象化后,就能清晰地看到它与现代神经网络训练在数学本质上的一致性。
02 自适应滤波器的核心思想
自适应滤波器的理论突破在于将传统滤波器的固定权重转变为可动态调整的参数系统。这一转变不仅扩展了信号处理的应用范围,更重要的是为机器学习中的参数优化提供了原型模型。从数学形式上看,自适应滤波器仍然保持线性组合的基本结构:
<math xmlns="http://www.w3.org/1998/Math/MathML"> y = ∑ i = 1 N w i x i = w T x y=\sum_{i=1}^Nw_ix_i=\mathbf{w}^T\mathbf{x} </math>y=∑i=1Nwixi=wTx
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> w w </math>w 为可调权重向量, <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 为输入信号向量。
自适应滤波器的创新性体现在其训练机制上。通过引入期望信号 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 作为监督信号,系统可以计算瞬时误差:
<math xmlns="http://www.w3.org/1998/Math/MathML"> e [ n ] = d [ n ] − y [ n ] e[n]=d[n]-y[n] </math>e[n]=d[n]−y[n]
并基于该误差动态调整滤波器权重。Widrow 和 Hoff 提出的最小均方(LMS)算法采用梯度下降思想,通过以下规则更新权重:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w [ n + 1 ] = w [ n ] + 2 μ e [ n ] x [ n ] \mathbf{w}[n+1]=\mathbf{w}[n]+2\mu e[n]\mathbf{x}[n] </math>w[n+1]=w[n]+2μe[n]x[n]
式中 <math xmlns="http://www.w3.org/1998/Math/MathML"> μ μ </math>μ 为学习率参数。这一更新规则与现代神经网络中的随机梯度下降(SGD)算法具有相同的数学本质,都是通过误差的反向传播来调整模型参数。
从系统结构来看,自适应滤波器已经包含了现代机器学习模型的三个关键组件:可训练的参数系统、误差评估机制以及参数更新算法。这种结构后来被直接应用于 ADALINE 神经网络,成为连接传统信号处理与神经网络的重要桥梁。值得注意的是,这种基于瞬时误差的在线学习方式,特别适合处理时序信号等流式数据,这一特性也被现代深度学习中的在线学习算法所继承。
03 最小均方(LMS)的诞生
自适应滤波器的理论价值在于其训练机制的创新性突破。Widrow 和 Hoff 提出的最小均方(LMS)算法,通过建立误差与权重之间的动态调整关系,首次实现了滤波器的在线学习能力。这一算法的核心思想源于对瞬时误差的数学优化,其推导过程展现了工程实践与理论创新的完美结合。
误差函数的定义是 LMS 算法的起点。对于第 <math xmlns="http://www.w3.org/1998/Math/MathML"> n n </math>n 个时刻的输入 <math xmlns="http://www.w3.org/1998/Math/MathML"> x [ n ] \mathbf{x}[n] </math>x[n],滤波器输出 <math xmlns="http://www.w3.org/1998/Math/MathML"> y [ n ] \mathbf{y}[n] </math>y[n] 与期望信号 <math xmlns="http://www.w3.org/1998/Math/MathML"> d [ n ] \mathbf{d}[n] </math>d[n] 之间的瞬时误差为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> e [ n ] = d [ n ] − y [ n ] = d [ n ] − w T [ n ] x [ n ] e[n]=d[n]-y[n]=d[n]-\mathbf{w}^T[n]\mathbf{x}[n] </math>e[n]=d[n]−y[n]=d[n]−wT[n]x[n]
为了建立可优化的目标函数,算法采用瞬时平方误差作为损失度量:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ξ [ n ] = e 2 [ n ] \xi[n]=e^2[n] </math>ξ[n]=e2[n]
通过对损失函数求权重向量的梯度,可以得到参数更新的方向:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ∇ [ n ] = ∂ ξ [ n ] ∂ w [ n ] = − 2 e [ n ] x [ n ] \nabla[n]=\frac{\partial\xi[n]}{\partial\mathbf{w}[n]}=-2e[n]\mathbf{x}[n] </math>∇[n]=∂w[n]∂ξ[n]=−2e[n]x[n]
基于梯度下降原理,权重更新规则可表示为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w [ n + 1 ] = w [ n ] − μ ∇ [ n ] = w [ n ] + 2 μ e [ n ] x [ n ] \mathbf{w}[n+1]=\mathbf{w}[n]-\mu\nabla[n]=\mathbf{w}[n]+2\mu e[n]\mathbf{x}[n] </math>w[n+1]=w[n]−μ∇[n]=w[n]+2μe[n]x[n]
式中 μ 为学习率参数,控制着参数更新的步长。
从计算效率角度看,LMS 算法具有明显的工程优势。每次迭代仅需 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( N ) O(N) </math>O(N) 次乘加运算( <math xmlns="http://www.w3.org/1998/Math/MathML"> N N </math>N 为滤波器阶数),这种线性复杂度使其能够实时处理高速数据流。此外,算法的收敛性可以通过学习率的选择来保证,当满足 <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 < μ < 1 λ m a x 0<\mu<\frac{1}{\lambda_{max}} </math>0<μ<λmax1 时( <math xmlns="http://www.w3.org/1998/Math/MathML"> λ m a x \lambda_{max} </math>λmax 为输入自相关矩阵的最大特征值),权重向量将收敛至最优解。
LMS 算法的随机性特征使其成为最早的随机梯度下降实例之一。与批量梯度下降不同,LMS 基于单个数据点立即更新参数,这种"即时学习"别适合非平稳信号处理。在后续发展中,这种在线学习思想被扩展为更复杂的自适应算法家族,包括归一化 LMS、仿射投影算法等,为现代深度学习中的优化方法提供了重要参考。
04 实践意义与学习建议
理解自适应滤波器的实现过程对于掌握机器学习基础原理具有独特的教学价值。从工程实践的角度来看,构建一个完整的自适应滤波系统能够帮助学习者直观理解三个关键概念:参数化模型的结构设计、损失函数的定义方式以及梯度下降算法的具体实现。这些概念构成了现代机器学习系统的核心框架。
在具体实现层面,建议采用分阶段开发策略。第一阶段可先构建固定权重的移动平均滤波器,通过这个简化模型验证数据流处理的正确性。这个阶段的重点在于掌握滑动窗口机制和向量化运算技巧,其核心计算可以表示为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> y [ n ] = 1 N ∑ k = 0 N − 1 x [ n − k ] y[n]=\frac{1}{N}\sum_{k=0}^{N-1}x[n-k] </math>y[n]=N1∑k=0N−1x[n−k]
第二阶段引入权重训练机制,将固定权重替换为可训练参数,并实现 LMS 算法的在线更新规则:
<math xmlns="http://www.w3.org/1998/Math/MathML"> w [ n + 1 ] = w [ n ] + 2 μ e [ n ] x [ n ] \mathbf{w}[n+1]=\mathbf{w}[n]+2\mu e[n]\mathbf{x}[n] </math>w[n+1]=w[n]+2μe[n]x[n]
这个阶段需要特别注意学习率 <math xmlns="http://www.w3.org/1998/Math/MathML"> μ μ </math>μ 的选择,过大的学习率会导致系统不稳定,而过小的学习率则会显著延长收敛时间。实验表明,对于大多数平稳信号,学习率设置在 0.01 到 0.1 之间通常能取得较好的平衡。
第三阶段着重于性能分析和可视化。除了直接观察时域波形外,建议采用频域分析方法评估滤波效果。快速傅里叶变换(FFT)能够清晰展示滤波器对特定频率成分的抑制效果,这种分析方法后来也广泛应用于深度学习模型的频域特性研究。
整个系统仅需基础的 Python 编程环境和 NumPy 库即可实现,无需 GPU 加速或复杂的深度学习框架。这种轻量级的实现方式使得学习者能够将注意力集中在算法原理本身,而不是框架使用的技术细节上。实验结果也表明,经过适当训练的 FIR 滤波器能够有效提取淹没在噪声中的目标信号,其性能往往优于传统的固定系数滤波器。
对于希望深入理解机器学习底层原理的实践者,建议将自适应滤波器的实现作为入门练习。这个过程中获得的经验可以直接迁移到更复杂的神经网络实现,特别是在理解反向传播算法和参数更新机制方面。现代深度学习框架中的优化器模块,其核心思想仍然延续了 LMS 算法的设计理念,只是扩展到了更高维的参数空间和非线性变换场景。
参考文献
1\] A. Ananthaswamy, Why machines learn: the elegant math behind modern AI. New York: Dutton, 2024. pgs 64--94. \[2\][ai.gopubby.com/the-first-l...](https://link.juejin.cn?target=https%3A%2F%2Fai.gopubby.com%2Fthe-first-learning-algorithms-adaptive-filters-f1fe9e0d0d61 "https://ai.gopubby.com/the-first-learning-algorithms-adaptive-filters-f1fe9e0d0d61") \[3\][leungyukshing.cn/archives/LM...](https://link.juejin.cn?target=http%3A%2F%2Fleungyukshing.cn%2Farchives%2FLMS.html "http://leungyukshing.cn/archives/LMS.html")