数据结构之B-树

系列文章目录

[1. B-树的性质](#1. B-树的性质)

[2. B-树的插入过程](#2. B-树的插入过程)

[编辑3. B-树插入过程的实现](#编辑3. B-树插入过程的实现)

[1. B-树节点的定义](#1. B-树节点的定义)

[2. B-树节点的插入](#2. B-树节点的插入)

[3. B-树的性能分析](#3. B-树的性能分析)

二、B+树

[1. B+树的性质](#1. B+树的性质)

[2. B+树的分裂](#2. B+树的分裂)

[3. B-树和 B+树的对比](#3. B-树和 B+树的对比)

三、B-树的应用

[1. 索引](#1. 索引)

[2. MyISAM 和 InnoDB](#2. MyISAM 和 InnoDB)

前言

本文介绍了B-树和B+树的基本性质、插入过程及实现方法。B-树是一种平衡多叉树，具有特定的节点关键字和子节点数量要求。文中详细演示了B-树的插入和分裂过程，并给出了Java实现代码。B+树与B-树类似，但所有关键字都出现在叶子节点，更适合文件索引系统。最后分析了两种树在MySQL索引中的应用差异，指出MyISAM使用B+树作为非聚集索引，而InnoDB采用聚集索引，数据文件本身就是索引文件。文章通过示例和代码展示，帮助理解这两种重要数据结构的特点和应用场景。

一、B-树

1. B-树的性质

B 树是一种平衡的多叉树。一棵 M (M > 2) 阶的 B 树，是一棵平衡的 M 路搜索树，可以是空树或者满足如下性质：

根节点至少有两个孩子；
每个非根节点至少有 M/2 - 1(向上取整) 个关键字，至多有 M - 1 个关键字，并且以升序排列；
每个非根节点至少有 M/2 (向上取整) 个孩子，至多有 M 个孩子；
key[i] 和 key[i + 1] 之间的孩子节点的值介于 key[i]、key[i + 1] 之间；
所有的叶子节点都在同一层；

2. B-树的插入过程

下面以三叉树为例，展示 B 树的插入过程；

注意：三叉树只有两个关键字，下面使用四叉树的节点演示三叉树的插入过程，多开一个空间的目的是目的是方便关键字的插入和提取中间节点；

用序列 {53, 139, 75, 49, 145, 36, 101} 构建B树的过程如下：

step1：按顺序依次插入53，139，75

插入时采用插入排序的方式，将值从小到达进行排序，如下图：

step2：节点分裂

分裂一个新的节点，将中间节点右边的值，拷贝到新的节点；

注意：将节点拷贝走的时候，同时也要拷贝它的子节点；

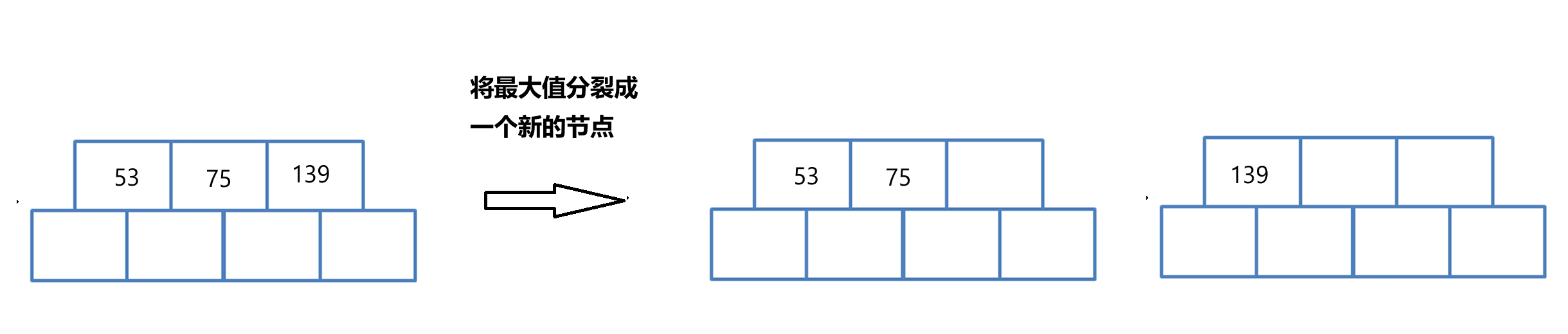
如果进行分裂的节点是根节点，还要将中间值再分裂成一个新的根节点；

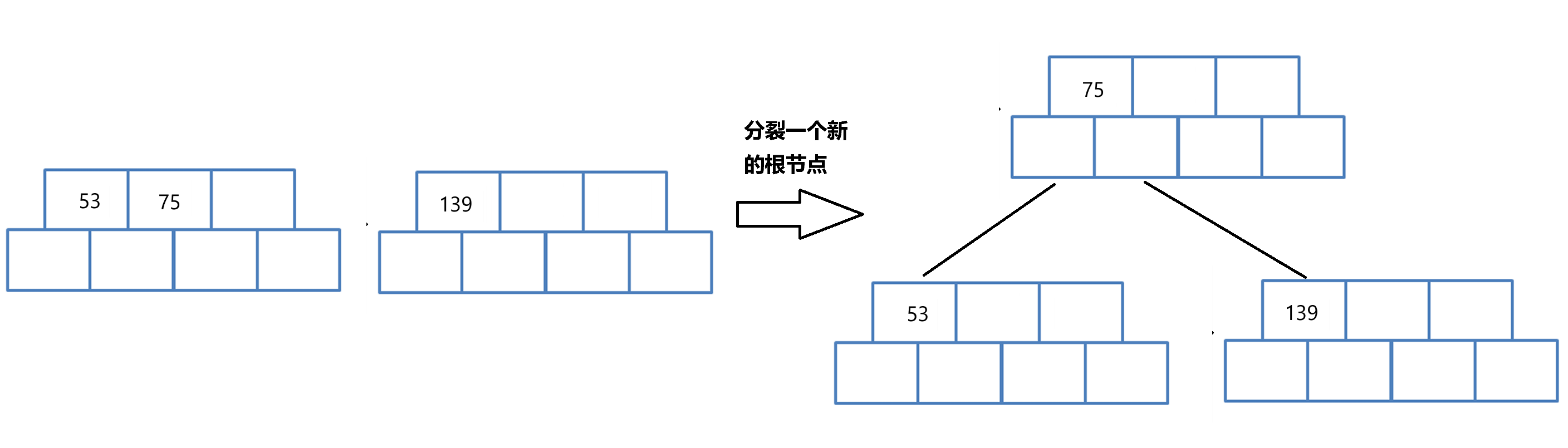step3：插入 49 和 145

step4：插入 36

按照插入排序的方式，插入 36；

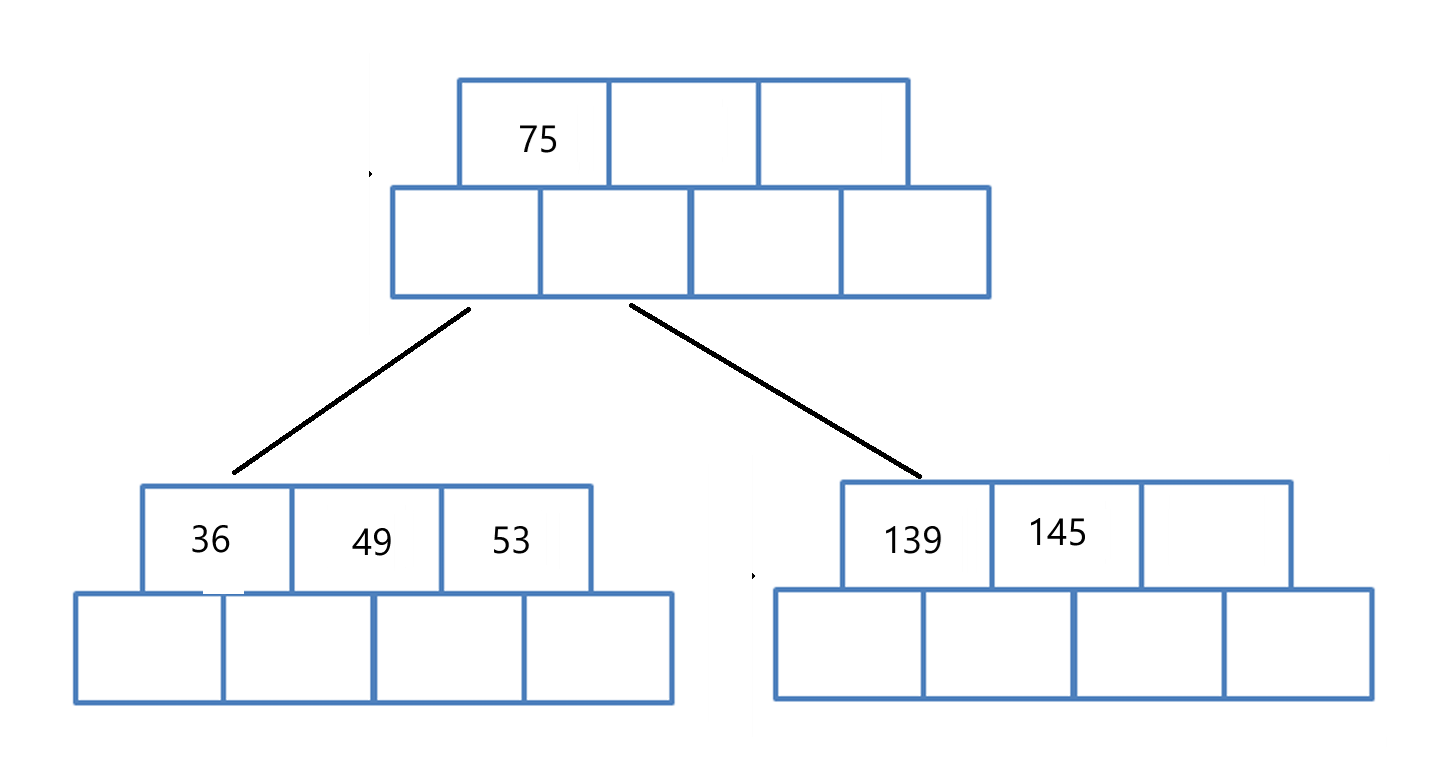
左下角节点元素个数已满，分裂一个新的节点，将中间节点后面的元素拷贝到新节点，并将中间节点提到根节点；

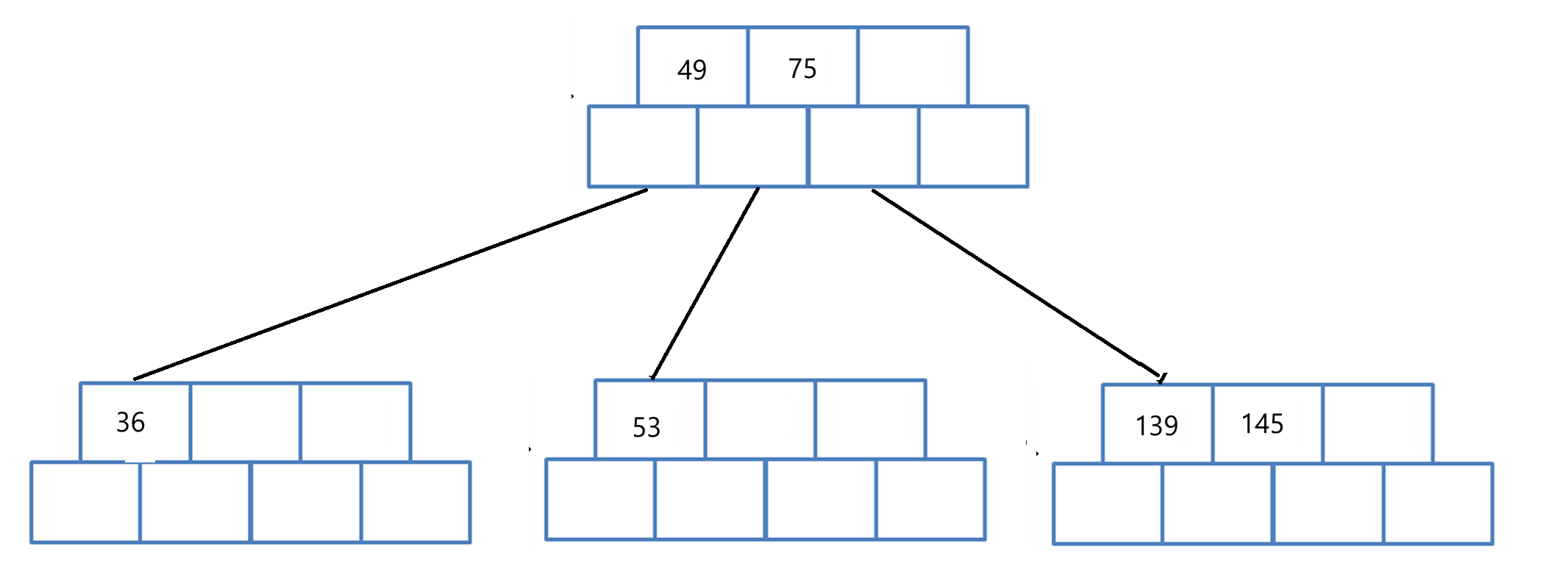
step5：插入数字 101

插入排序的方式插入 101；

右边节点已满，分裂一个新节点，中间节点后面的元素都拷贝到新节点，并将中间元素提到根节点；

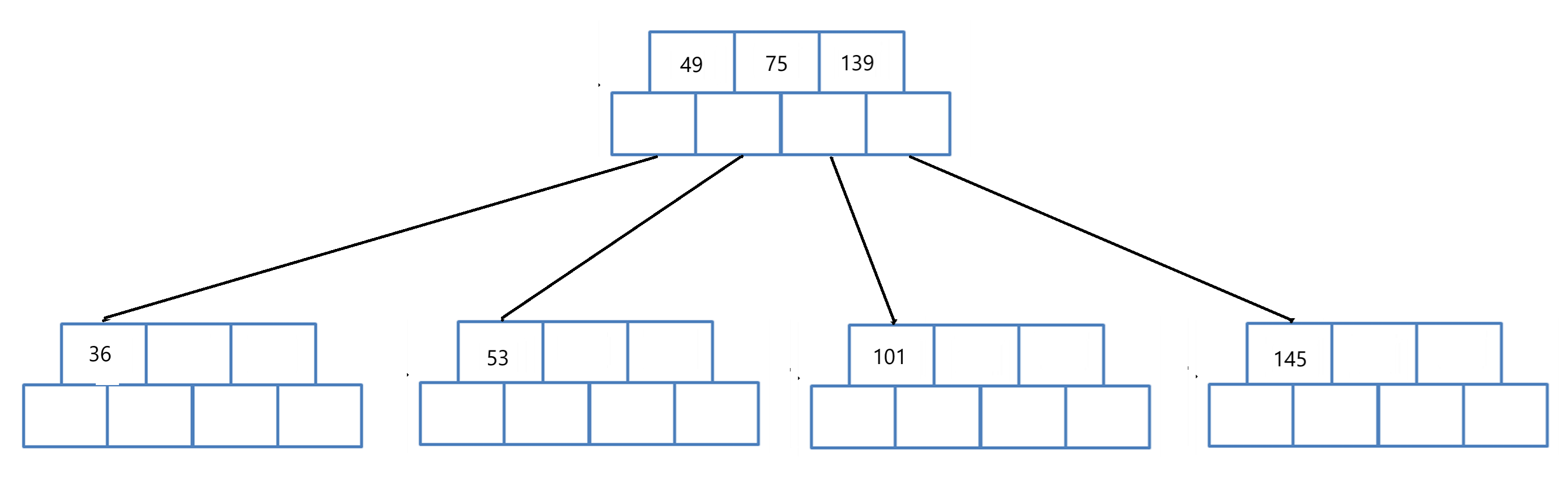
根节点已满，分裂一个新的节点将中间节点右边的元素都拷贝到新节点，并创建新的根节点，将中间元素提到新的节点；

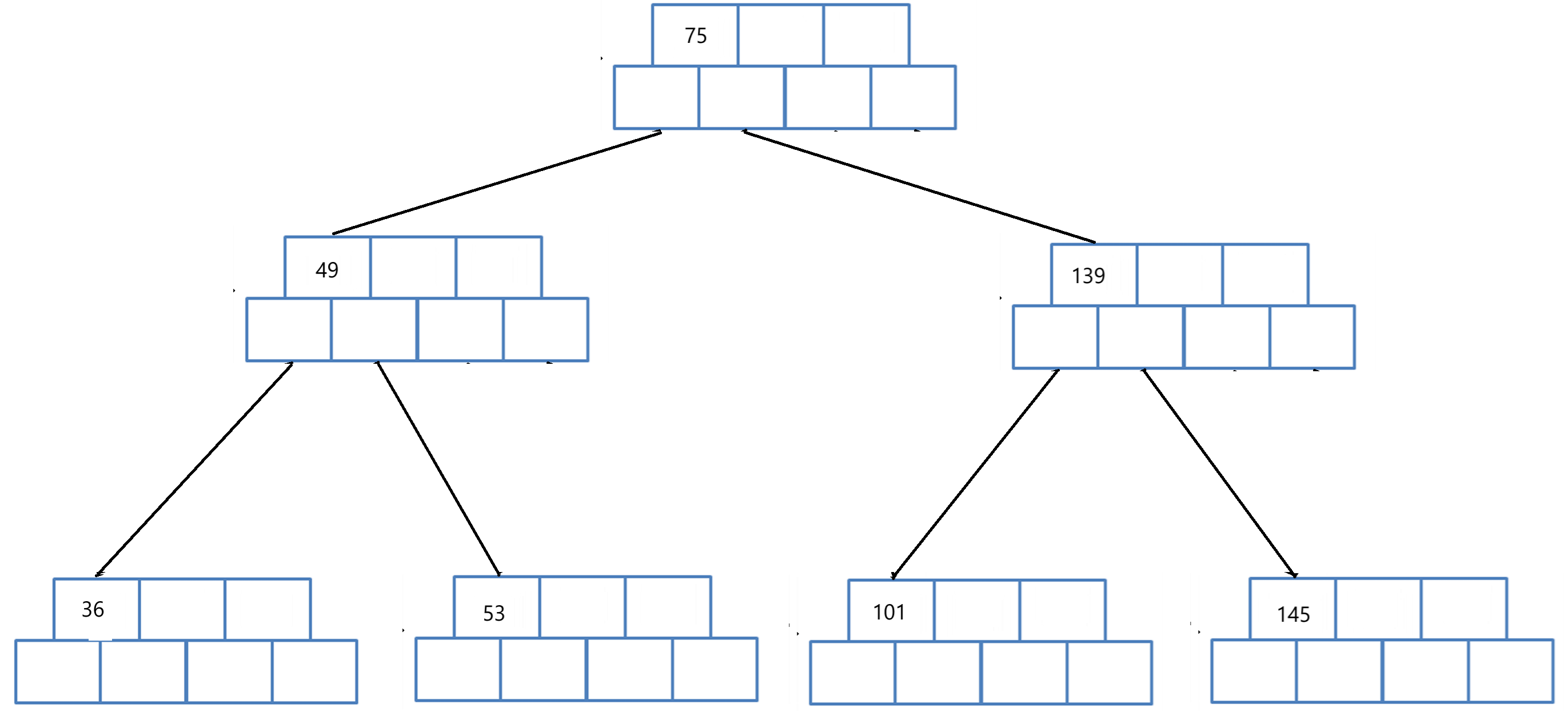3. B-树插入过程的实现

1. B-树节点的定义

keys 存放关键字；

subs 存放子节点；

parent 父亲节点；

usedSize 维护关键字的数量；

BTRNode() 构造方法，初始化关键字数组，子节点数组，初始化时，多开一个空间，方便关键字的插入和提取；

java 复制代码

    static class BTRNode{
        public int[] keys;
        public BTRNode[] subs;
        public BTRNode parent;
        public int usedSize;

        public BTRNode(){
            // 为了方便分裂，需多开辟一个空间
            this.keys = new int[M];
            this.subs = new BTRNode[M + 1];
            this.usedSize = 0;
            this.parent = null;
        }
    }

2. B-树节点的插入

M 表示三叉树；

root 表示根节点；

insert(int key): boolean 在 B-树中插入节点；

实现思路：

1. 如果根节点为空，表示 B-树为空，新插入的节点成为根节点；
1. 如果要插入的节点，在 B-树中存在，不需要再插入，返回 false 即可；
1. 采用搜索树的方式，找到关键字 key 要插入的节点，将关键字以插入排序的方式进行插入；
1. 插入完成后，检查当前节点的关键字数量，如果超过 M，需要将节点进行分裂；

findKey(int key): Pair<BTRNode, Integer> 找到关键字要插入的节点；

实现思路：

1. 从根节点开始，遍历节点的关键字数组；
1. 如果要插入的关键字的值等于当前关键字的值，表示关键字已存在，不需要进行插入，直接返回当前节点即可；
1. 如果要插入的关键字的值大于当前关键字的值，继续往后遍历；
1. 如果要插入的关键字的值小于当前关键字的值，跳出查找关键字循环，继续遍历当前节点左边的子节点，重复 2 ~ 4 过程；
1. 如果当前节点为空，当前节点的父亲节点就是关键字要插入的节点，但是因为位置不确定，因此返回父亲节点；

注意：

因为在 insert() 方法中，我们无法区别返回的是当前节点还是父亲节点，也不知道当前的关键字是否在 B-树中存在，因此这里不能简单返回一个节点，而是返回一个数对 Pair<BTRNode, Integer>；
数对中的整数如果为 -1 表示当前返回的节点是父亲节点，要插入的下标未知，用 -1 表示；
数对中的整数如果为大于等于 0 的数字表示返回的节点为 cur 节点，关键字的下标用该数字表示；

split(BTRNode cur): void 分裂当前节点；

实现思路：

1. 确定当前节点的关键字数组右中点的下标 mid，建立一个新的节点；
1. 将右中点右边的关键字都拷贝到新节点当中，同时将关键字的子节点也拷贝到新节点当中；同时也要将关键字的子节点的父亲节点设置为新节点；
1. 维护新节点关键字的数量，以及当前节点关键字的数量；
1. 判断当前节点是否为根节点，如果是根节点，需要再新建一个节点作为新的根节点，将当前节点 mid 下标指向的关键字拷贝到新的根节点当中；新根节点的子节点数组，0 下标指向当前节点，1 下标指向新节点；同时将当前节点和新节点的父亲节点都设置为新节点；
1. 如果当前的节点不是根节点，将 mid 下标的关键字拷贝到当前节点的父亲节点的关键字数组中，同时将关键字的右子节点设置为新节点；新节点的父亲节点指向当前节点的父亲节点，并维护父亲节点的关键字的数量；
1. 判断父亲节点的关键字数量是否超过 M，如果超过，对父亲节点再进行分裂；

java 复制代码

public class MyBTree {    
    public static final int M = 3;
    public BTRNode root;

    public boolean insert(int key){
        // 1. 插入之前要先判断 B 树是否为空
        if(this.root == null){
            BTRNode node = new BTRNode();
            node.keys[0] = key;
            node.usedSize++;
            this.root = node;
            return true;
        }
        // 2. 插入之前要先在 B 树中找，看 key 是否存在
        Pair<BTRNode, Integer> ret = findKey(key);
        // 3. 如果找到了 key，就不用再插入了
        if(ret.getValue() != -1){
            return false;
        }
        // 4. 如果没找到 key，需要进行插入
        BTRNode cur = ret.getKey();
        int i = cur.usedSize - 1;
        for( ; i >= 0; i--){
            if(cur.keys[i] >= key){
                cur.keys[i + 1] = cur.keys[i];
            }else{
                break;
            }
        }
        cur.keys[i + 1] = key;
        cur.usedSize++;
        // 5. 如果插入后的 cur.usedSize >= M - 1，需要进行分裂
        if(cur.usedSize >= M){
            split(cur);
            return true;
        }else{
            return true;
        }
    }

    private void split(BTRNode cur) {
        // 创建一个新的节点 - 放在右边
        BTRNode newNode = new BTRNode();
        // 将原来节点的一半值移到新节点中
        int mid = cur.usedSize / 2;
        int i = mid + 1;
        int j = 0;

        for( ; i < cur.usedSize; i++){
            // 不仅要移动 key 值，还要移动它的孩子节点
            newNode.keys[j] = cur.keys[i];
            newNode.subs[j] = cur.subs[i];
            // 处理刚拷贝过来的孩子节点的父亲节点
            if(cur.subs[i] != null){
                cur.subs[i].parent = newNode;
            }
            j++;
        }
        newNode.subs[j] = cur.subs[i];
        if(cur.subs[i] != null){
            cur.subs[i].parent = newNode;
        }
        // 更新 newNode, cur 的 usedSize
        newNode.usedSize = j;
        cur.usedSize = mid;

        // 处理分裂根节点的情况
        if(cur == root){
            BTRNode newRoot = new BTRNode();
            newRoot.keys[0] = cur.keys[mid];
            newRoot.subs[0] = cur;
            cur.parent = newRoot;
            newRoot.subs[1] = newNode;
            newNode.parent = newRoot;
            newRoot.usedSize = 1;
            root = newRoot;
            return;
        }

        // 如果分裂的 cur 节点不是根节点
        BTRNode parent = cur.parent;
        // 将节点的 mid 位置的值，移动向父节点
        int pIndex = parent.usedSize - 1;
        for( ; pIndex >= 0; pIndex--){
            if(parent.keys[pIndex] >= cur.keys[mid]){
                // 不仅要移动 key，还要移动子节点
                parent.keys[pIndex + 1] = parent.keys[pIndex];
                parent.subs[pIndex + 2] = parent.subs[pIndex + 1];
            }else{
                break;
            }
        }
        parent.keys[pIndex + 1] = cur.keys[mid];

        newNode.parent = parent;
        parent.subs[pIndex + 2] = newNode;
        // 更新 parent 的 usedSize
        parent.usedSize++;

        if(parent.usedSize >= M){
            split(parent);
        }
    }

    private Pair<BTRNode, Integer> findKey(int key) {
        BTRNode cur = root;
        BTRNode parent = null;
        while(cur != null){
            int index = 0;
            while(index < cur.usedSize){
                if(cur.keys[index] < key){
                    index++;
                }else if(cur.keys[index] > key){
                    break;
                }else{
                    return new Pair<>(cur, index);
                }
            }
            parent = cur;
            cur = cur.subs[index];
        }
        return new Pair<>(parent, -1);
    }
}

3. B-树的性能分析

对于一棵度为 M，总节点个数为 N 的 B-树，高度在 log(M-1)N ~ log(M/2)N 之间，定位到节点后，利用二分查找，能很快定位到要查找的元素，性能非常高；

例如：N = 62 * 1000000000，如果 M = 1024，则 log(M/2)N = 3.59，即表示 620亿数据，通过 4 次查找就可定位元素的节点，再通过二分查找，最多 10 次就可以找到元素，大大减少了 IO 的次数；

二、B+树

1. B+树的性质

B+树与 B-树的搜索基本相同，区别是 B+树只有达到叶子节点才能命中，性能等价于在关键字全集中做一次二分查找；

非叶子节点的子树个数和关键字个数相同；
非叶子节点的子树指针 p[i]，指向关键字值属于 key[i] ~ key[i + 1] 之间的子树；
为所有的叶子节点增加了一个链指针；
所有的关键字都在叶子节点出现；

B+树的特性：

所有关键字都出现在叶子节点的链表中（稠密索引），且链表中的节点都是有序的；
不可能在非叶子节点命中；
非叶子节点相当于是叶子节点的索引（稀疏索引），叶子节点相当于是存储数据的数据层；
更适合文件索引系统；

2. B+树的分裂

当一个节点满时，分配一个新的节点，并将原节点中 1/2 的数据复制到新节点，最后在父亲节点中增加新节点的指针；

B+树的分裂只影响原节点和父亲节点，不影响兄弟节点；

3. B-树和 B+树的对比

B-树是多路搜索树，每个节点存 M/2 - 1 ~ M - 1 个关键字，非叶子节点存储指向关键字范围的子节点；

所有的关键字在整棵树中出现，且只出现依次，非叶子节点可以命中；

B+树在 B-树的基础上为叶子节点增加链表指针，所有的关键字都在叶子节点出现，非叶子节点作为叶子节点的索引，B+树总是到叶子节点才能命中；

三、B-树的应用

1. 索引

B-树最常见的应用就是用来做索引；

索引是一种高效获取数据的数据结构；

在 MySQL 中，索引属于存储引擎级别的概念，不同存储引擎实现索引的方式不同；

索引是基于表的，不是基于数据库的；

2. MyISAM 和 InnoDB

MyISAM 存储引擎不支持事务；

MyISAM 使用 B+树作为索引结构，叶节点的 Data 域存放的是数据的地址，这种索引方式是非聚集索引；

MyISAM 中索引文件和数据文件是分离的（只保存数据的地址）；

MyISAM 中主索引和辅助索引的结构是相同的，区别是主索引不可重复，辅助索引可以重复；

InnoDB 是存储引擎支持事务；

InnoDB 存储引擎是 MySQL 默认的存储引擎；

InnoDB 中数据文件本身就是索引文件，其中叶节点的 Data 域保存了完整的数据结构，这种索引方式是聚集索引；

InnoDB 数据文件本身是按主键聚集，因此 InnoDB 要求必须表必须有主键；

如果不显式指定主键，MySQL 会自动选择一个可以唯一表示数据的列作为主键，如果不存在这种列，MySQL 会自动为 InnoDB 表生成一个隐含字段作为主键，字段为 6 个字节，类型为长整型；

InnoDB 的辅助索引的 Data 域存储的是主键的值，并非地址，查询过程为检索辅助索引获得主键，再使用主键去主索引中检索，获得记录，因此需要检索两遍索引；

使用主键索引检索效率非常高，如果使用辅助索引，效率会降低；