暑期算法训练.3

目录

[11.力扣 209.长度最小的子数组](#11.力扣 209.长度最小的子数组)

[11.1 题目解析：](#11.1 题目解析：)

[11.2 算法思路：](#11.2 算法思路：)

[11.3 代码演示：](#11.3 代码演示：)

​编辑

[11.4 总结反思：](#11.4 总结反思：)

[12. 力扣 LCR 016 无重复字符的最长子串](#12. 力扣 LCR 016 无重复字符的最长子串)

[12.1 题目解析：](#12.1 题目解析：)

[12.2 算法思路：](#12.2 算法思路：)

[12.3 代码演示：](#12.3 代码演示：)

​编辑

[12.4 总结反思：](#12.4 总结反思：)

[13.力扣 1004.最大连续1的个数III](#13.力扣 1004.最大连续1的个数III)

[13.1 题目解析：](#13.1 题目解析：)

[13.2 算法思路：](#13.2 算法思路：)

[13.3 代码演示：](#13.3 代码演示：)

​编辑

[13.4 总结反思：](#13.4 总结反思：)

[14.力扣 1658 将x减到0的最小操作数](#14.力扣 1658 将x减到0的最小操作数)

[14.1 题目解析：](#14.1 题目解析：)

​编辑

​编辑

[14.2 算法思路：](#14.2 算法思路：)

[14.3 代码演示：](#14.3 代码演示：)

[14.4 总结反思：](#14.4 总结反思：)

---

今天讲的题目都是滑动窗口系列的题目：

11.力扣 209.长度最小的子数组

11.1 题目解析：

本题目呢，你就光阅读这个题目的话 ，其实也挺好想的，就是找到某段区间的元素的和大于等于target，并且返回这两个元素的最小的长度。

11.2 算法思路：

这道题目如果是用暴力求解的话，也是可以解出来的，就是容易超时。并且暴力求解的思路其实也挺简单的。就是先固定住一边，然后再定义一个变量，使得它从头开始遍历，然后找出某段区间的元素和大于等于target即可。并且在这些符合的区间内，找到长度最小的即可。咱们来简单的看一下伪代码即可：

 for (int start = 0; start < n; start++)
      for (int end = start; end < n; end++)
        check()

咱们重点讲解的是第二种思路：也就是滑动窗口：

1.一般滑动窗口适用于区间长度大于等于0的情况

2.滑动窗口一般适用于找连续子串的题目

3.滑动窗口，肯定有划入，也有划出。划出的话，要检查划出的条件是什么，想清楚再写，否则会搞混乱。

4.滑动窗口一把就是双指针，但是这个双指针得是同向双指针（后面的题会有讲解）。

OK，本题的解题思路就是上面的，以及下面的三道题，跟这道题目的解题思路差不了多少。大家仔细的读一下。

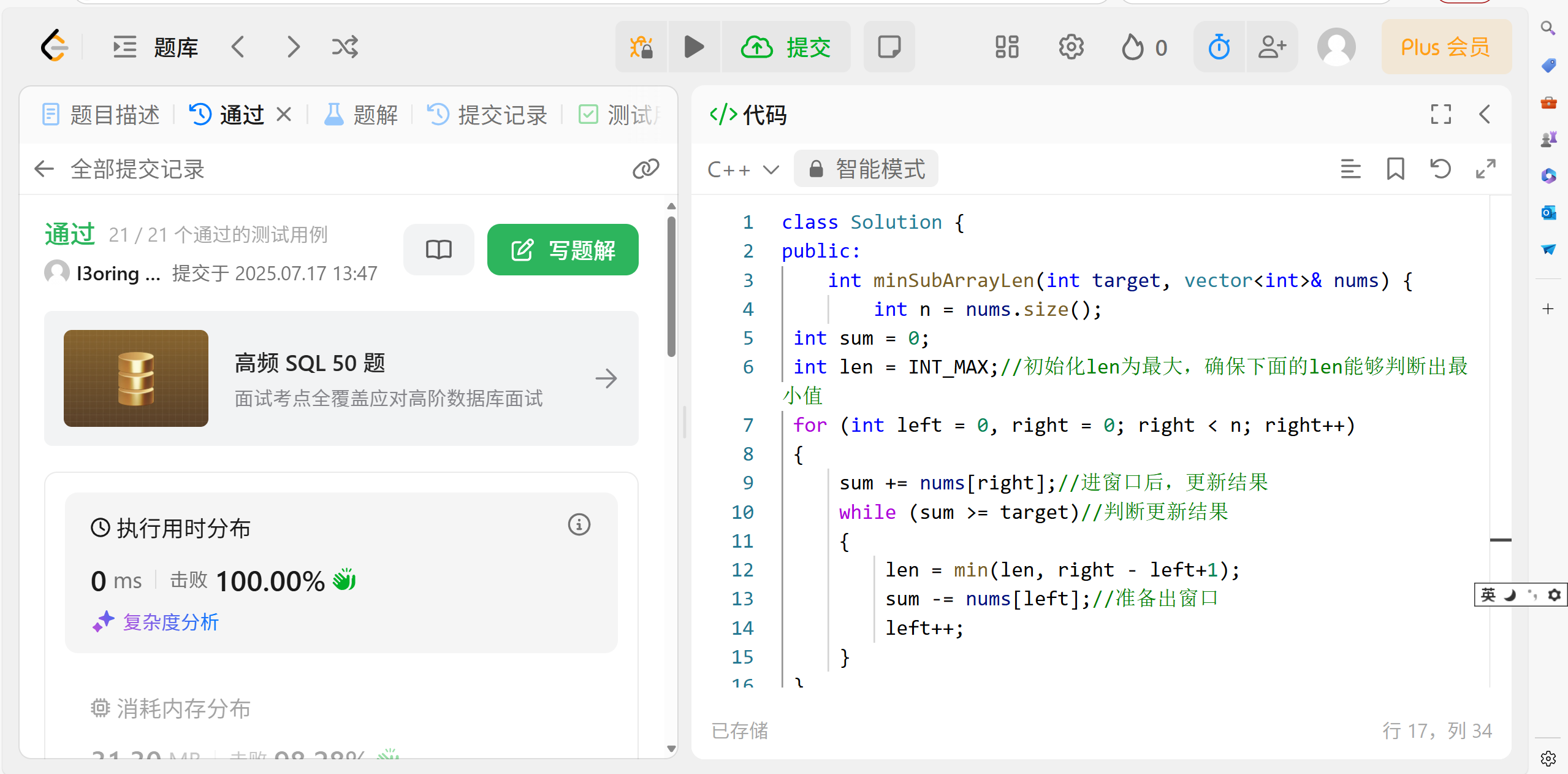
11.3 代码演示：

int minSubArrayLen(int target, vector<int>& nums) {
    int n = nums.size();
    int sum = 0;
    int len = INT_MAX;//初始化len为最大，确保下面的len能够判断出最小值
    for (int left = 0, right = 0; right < n; right++)
    {
        sum += nums[right];//进窗口后，更新结果
        while (sum >= target)//判断更新结果
        {
            len = min(len, right - left+1);
            sum -= nums[left];//准备出窗口
            left++;
        }
    }   
    return len == INT_MAX ? 0 : len;
}
int main()
{
    vector<int> nums = { 2,3,1,2,4,3 };
    int target = 7;
    int ret = minSubArrayLen(target, nums);
    cout << ret << endl;
}

这里呢，别搞晕了。作者第一次写这个代码的时候，就搞晕了，哪里晕了呢？就是外层循环是right（就是进入窗口），而内层的循环才是判断出窗口的条件。若是sum一直小于target，则外层循环就会一直执行.内层循环是执行判断->更新结果->出窗口的.

11.4 总结反思：

这里还有一点需要强调的是：这个代码的时间复杂度可是O（N），N为数据个数。不是O（N^2），因为这里的right不回头，它只往右边走。left也只往右边走，这样的话，每一个数只被访问了2次，就是O（2N）。而咱们平常的O（N^2)是right从头开始了，所以说，left走到每一个元素的时候，前面的每个元素均被访问了一遍。

12. 力扣 LCR 016 无重复字符的最长子串

12.1 题目解析：

注意题目中的子串：就是连续的一段。子数组：也是连续的一段。例如这样的都可以使用滑动窗口来做。

12.2 算法思路：

咱们这一题主要使用了滑动窗口的思想。这里需要用到一个哈希数组。下面来看一下思路讲解吧：

其实还是蛮简单的。理清楚思路之后，挺简单的。

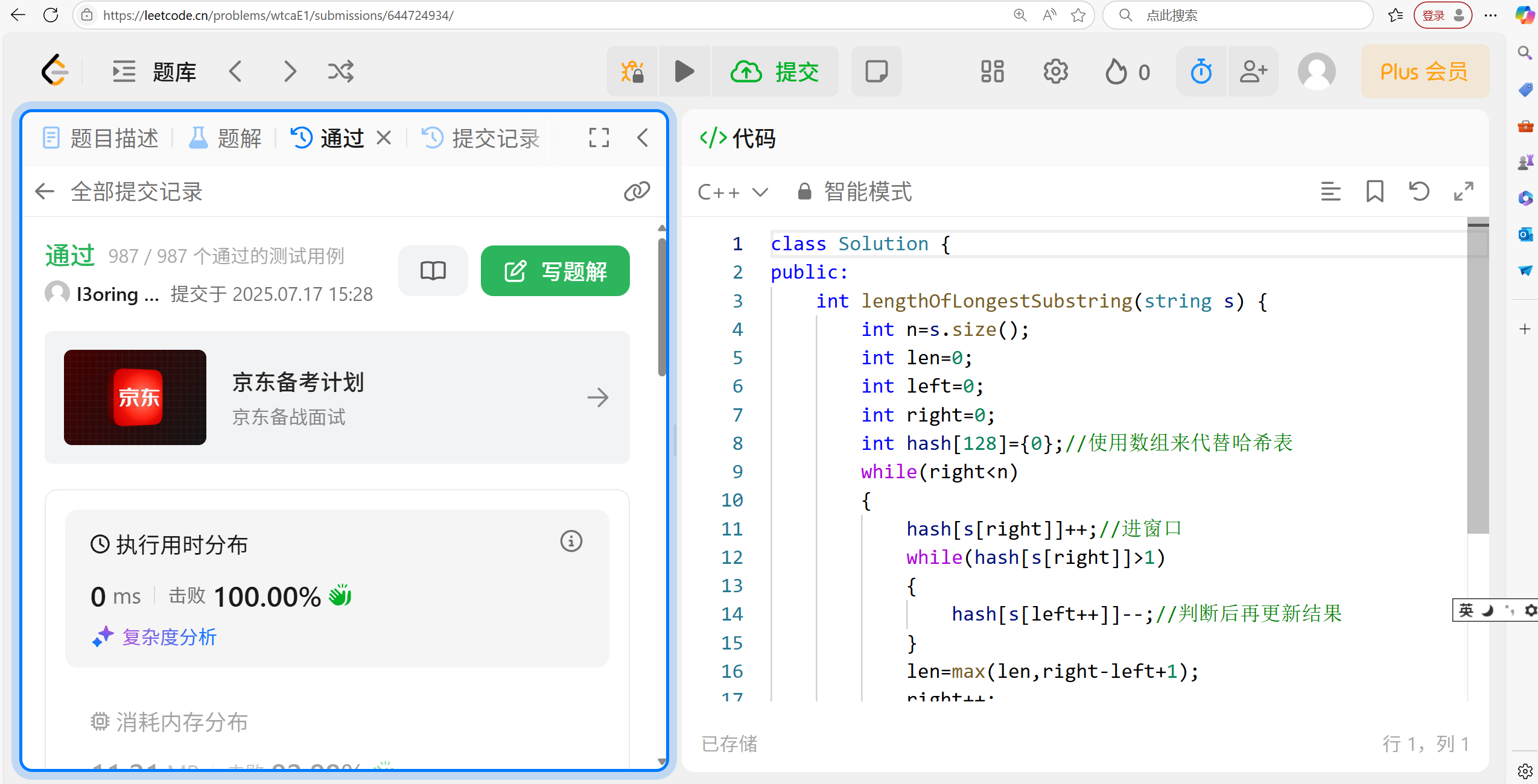
12.3 代码演示：

int lengthOfLongestSubstring(string s) {
    int n = s.size();
    int len = 0;
    int left = 0;
    int right = 0;
    int hash[128] = { 0 };//使用数组来代替哈希表
    while (right < n)
    {
        hash[s[right]]++;//进窗口
        while (hash[s[right]] > 1)
        {
            hash[s[left++]]--;//判断后再更新结果
        }
        len = max(len, right - left + 1);
        right++;
    }
    return len;
}
int main()
{
    string s("abcabcbb" );
    cout << lengthOfLongestSubstring(s) << endl;
    return 0;
}

这个len不需要再设为整数的最大范围了，因为这个本身不需要了。

12.4 总结反思：

滑动窗口的题目其实很简单。但是难的是，你要如何想到使用滑动窗口去做，还是要把握住那几点重要的特征才可以。

13.力扣 1004.最大连续1的个数III

13.1 题目解析：

这个题目，大家要是按照他这个题意去做，挺难的。翻转k个0，就是将0翻转为1.是这个意思。

那咱们可不可以换一种思路呢？就是正难则反。 所以这个题的题意就是找到一个连续的区间，使得0的个数不超过k个子数组。看看是不是这个意思。

13.2 算法思路：

这道题也是使用了滑动窗口来解决。不过要加上一个0计时器来作为判断出窗口的条件。

下面来看一下思路吧：

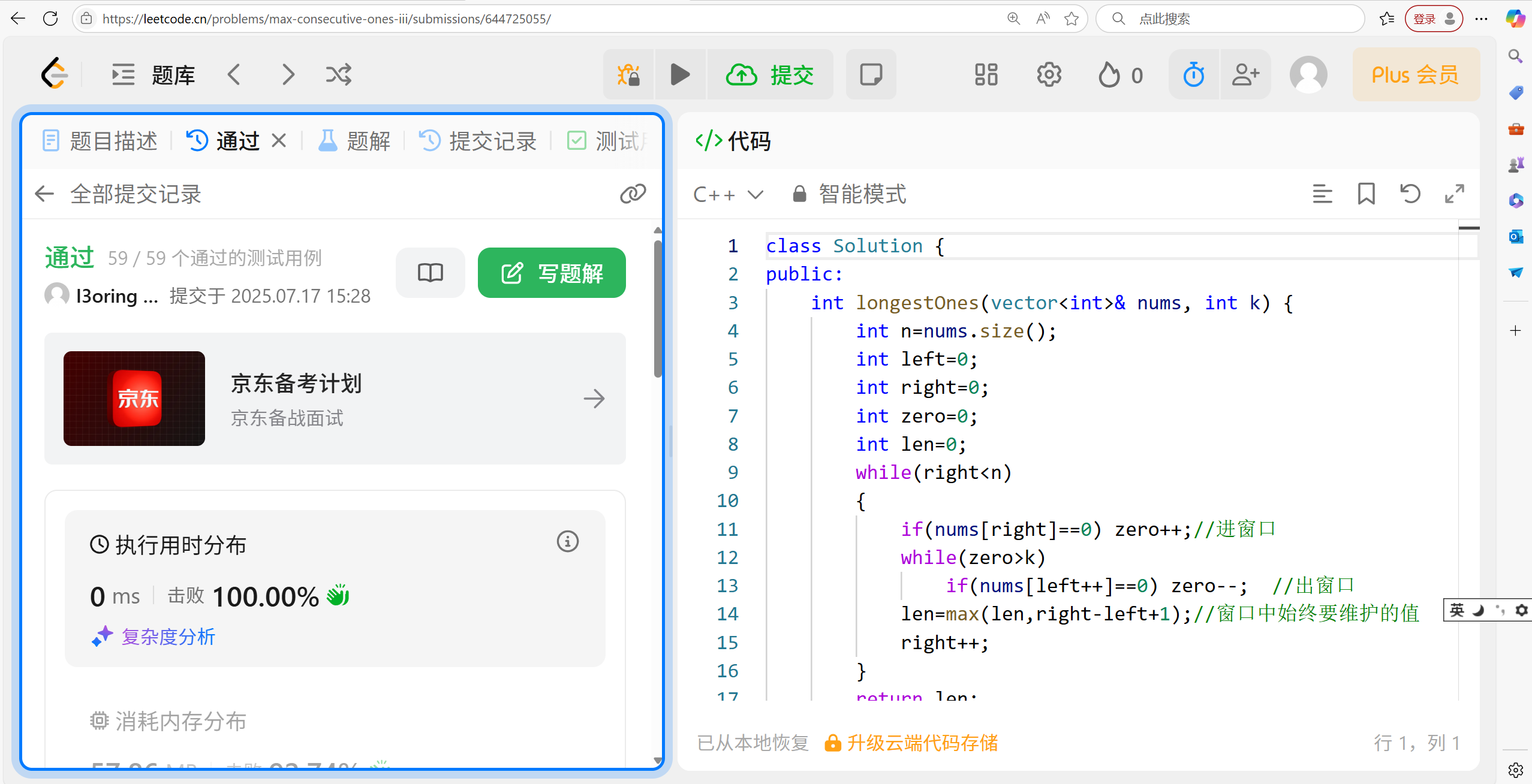
13.3 代码演示：

int longestOnes(vector<int>& nums, int k) {
    int n = nums.size();
    int left = 0;
    int right = 0;
    int zero = 0;
    int len = 0;
    while (right < n)
    {
        if (nums[right] == 0) zero++;//进窗口
        while (zero > k)
            if (nums[left++] == 0) zero--;  //出窗口
        len = max(len, right - left + 1);//窗口中始终要维护的值
        right++;
    }
    return len;
}
int main()
{
    vector<int> nums = { 1,1,1,0,0,0,1,1,1,1,0 };
    int k = 2;
    cout << longestOnes(nums, k) << endl;
    return 0;
}

代码你会发现，与之前的那些题目的代码大差不差。大相径庭。重要的是搞懂原理以为为什么使用滑动窗口来解决问题。

13.4 总结反思：

对于这种求连续区间的，一般使用的都是滑动窗口来解决。

14.力扣 1658 将x减到0的最小操作数

14.1 题目解析：

这道题也是够别扭的。博主花了很长的时间，就根据这个题目的意思来做的，结果做的一塌糊涂。因为这样做的话，题目的可能性太多了，而且代码贼多，就我当时写的，就有100多行。最终，博主还是放弃了，不是因为我半途而废。是因为我确实不会，上次一道题搞了6h，结果最后发现是方法用错了，所以还是要告诫大家，方法选对了比努力更重要，哈哈哈哈。

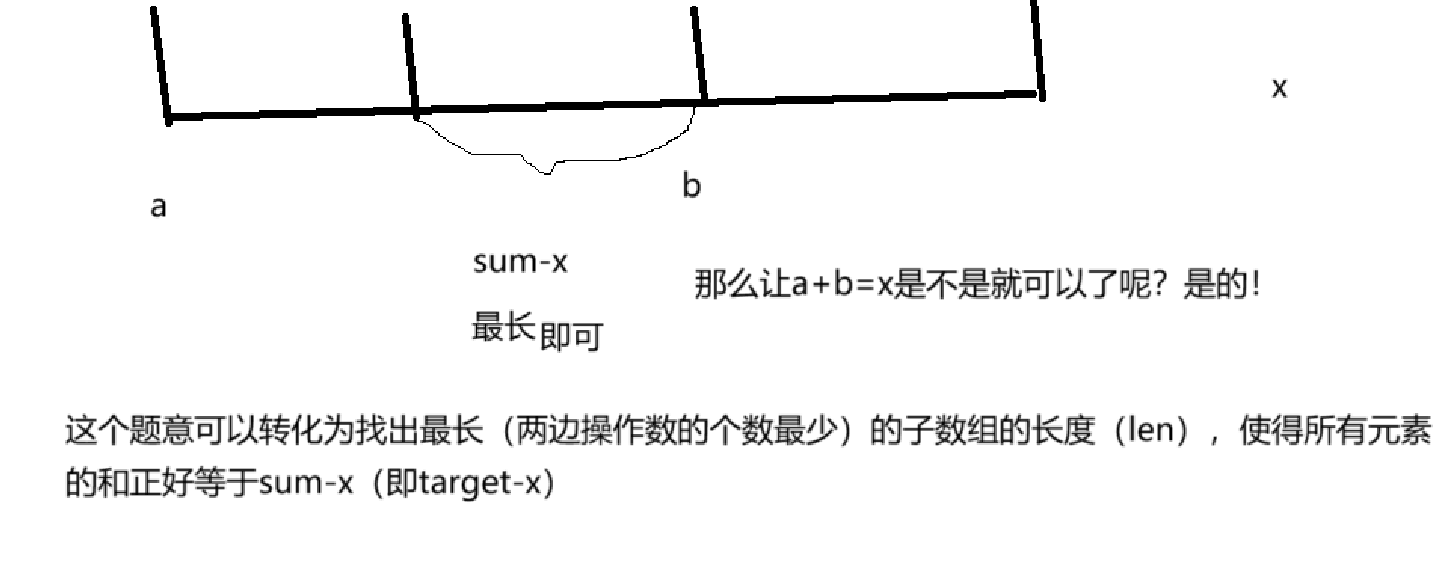
好了，回归题目，这种题，直接做很那做。所以正难则反，咱们可以从反面来寻找突破口。

好了那么现在是不是就思路清楚多了？咱们还是使用滑动窗口来解决这道题目：

14.2 算法思路：

那么滑动窗口，怎么个滑动法呢？

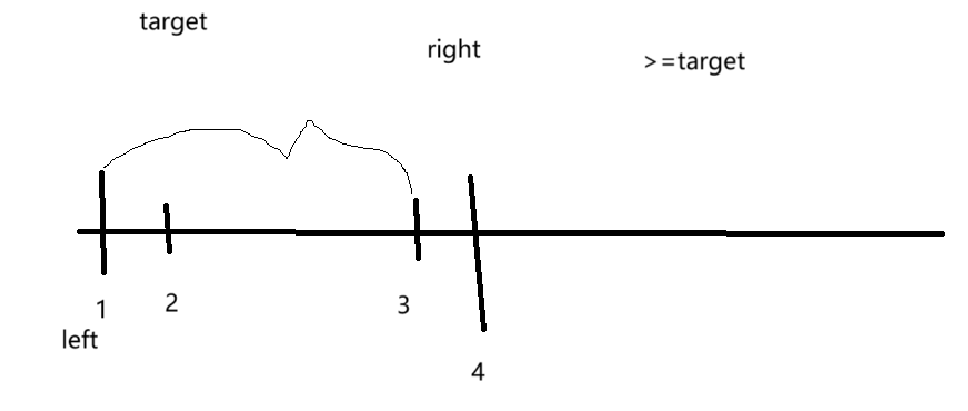
1.还是先让left与right从头开始。

2.开始进窗口，那么进窗口，是sum+=nums[right]。这个应该没什么疑问吧。就是右边的进窗口。

3.然后，开始判断出窗口的条件：sum>target(sum=target不可以，因为这个是咱们想要的结果，那sum都等于target了，还出什么窗口？）。出窗口后，sum-=nums[left++].(因为sum大于target，所以得让sum变小，直到sum==target为止）。

4.更新结果sum==target。

5.重复2-4步骤，直到找到为止。

那么大家思考一个问题？为什么right要一直往右边挪动，不往回走呢？因为right往回走毫无意义！

还是上图：2-3之间一定是小于target的，因为到了right这个点，恰好大于等于target，而这个点再往左挪动一个数，就是小于target。那你left挪动2的位置，如果right再从头开始走，不是一只都是小于target的嘛？那这样的话，right从头开始走还有啥意义？（明知道小于了，就不要再继续了。都摆在明面上事情，就别去重复了）所以，right要往右边走，left也要往右边走。

14.3 代码演示：

int minOperations(vector<int>& nums, int x) {
    int n = nums.size();
    int sum1 = 0;
    for (auto& e : nums)
    {
        sum1 += e;
    }
    int target = sum1 - x;
    if (target < 0)
    {
        return -1;//滑动区间只能在区间长度大于等于0内进行滑动
    }
    int left = 0;
    int right = 0;
    int len = -1;
    int sum = 0;
    while (right < n)
    {
        sum += nums[right];//进窗口
        while (sum > sum1 - x)
        {
            sum -= nums[left++];//出窗口。如果不加上那个判断target的语句的话，这里会报栈溢出的错误，因为sum一定是一个正数，那万一sum1-x是一个负数，这不是死循环了吗？
        }
        if (sum == sum1 - x)
        {
            len = max(len, right - left + 1);
        }
        right++;
    }
    if (len == -1)//说明不存在这个区间使得和等于sum1-x
    {
        return -1;
    }
    else
    {
        return n - len;
    }
}
int main()
{
    vector<int> nums = { 1,1,4,2,3 };
    int x = 5;
    cout << minOperations(nums, x) << endl;
    return 0;
}

这段代码也有很多细节。我都写在代码上面了，大家自行观看。

14.4 总结反思：

关于这个正难则反的问题，博主还是不够熟练，还需要勤加练习才可以。