文章目录
前言
通过今天的学习,我掌握了构建神经网络中的相关概念,包括激活函数,参数初始化,损失函数的基础概念和用法。
一、激活函数
激活函数是构建神经网络的核心概念,使得模型具备非线性,从而学习更加复杂的关系,大大提高模型的表达能力。
常见的激活函数包括:sigmoid函数,tanh函数,ReLU函数,Softmax函数。
1.sigmoid函数
sigmoid函数将模型的输入映射到0~1之间,常常用于处理二分类问题 。
f ( x ) = σ ( x ) = 1 1 + e − x f(x) = \sigma(x) = \frac{1}{1 + e^{-x}} f(x)=σ(x)=1+e−x1
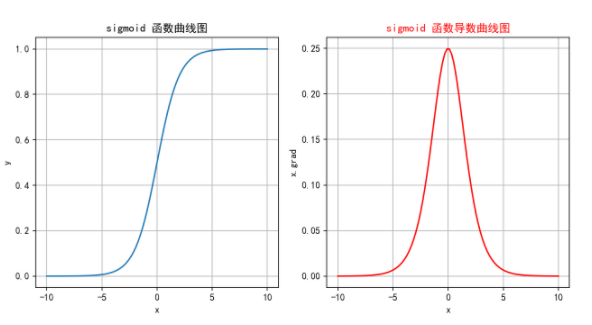
通过函数的图像,我们可以发现:
1.sigmoid函数的导数最大值为0.25,因此在反向传播的迭代过程中可能导致结果趋近于0,从而使得梯度消失 。
2.如果输入值太大或太小,函数梯度值几乎不发生变化,此时会导致尽管输入有较大差异而梯度几乎没有区别,造成信息丢失 。
3.函数设计指数运算,计算开销较大。
2.tanh函数
tanh函数与sigmoid函数类似,一般也应用于分类问题,但一般不推荐使用。
x t a n h ( x ) = e x − e − x e x + e − x x{tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} xtanh(x)=ex+e−xex−e−x
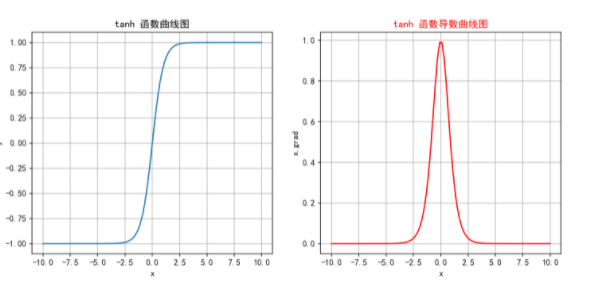
结合图像,tanh函数与sigmoid函数都存在梯度消失的问题,但由于tanh函数导数的值域范围更广,发生梯度消失的速度没那么快;计算性能同样无法保证。
但tanh函数将函数映射到:-1~1之间,使得输出零中心化,更加利于计算收敛。
3.ReLU函数
基于sigmoid函数和tanh函数存在梯度消失的问题,引入一种简单而高效的激活函数------ReLU函数(修正线性单元)。
ReLU ( x ) = max ( 0 , x ) \text{ReLU}(x) = \max(0, x) ReLU(x)=max(0,x)
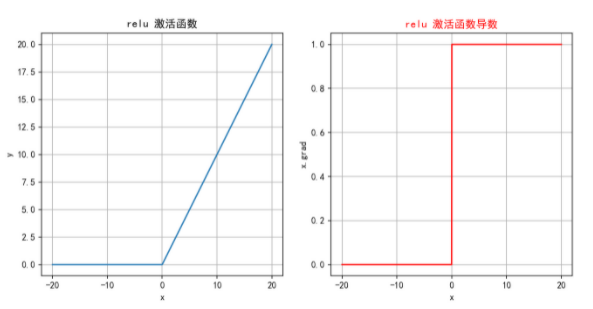
ReLU函数的定义十分简单,使得在计算过程中更加高效;同时,在函数的正半部分,导数恒为1,有效缓解了梯度消失的问题。
但由于函数定义输出小于0的部分输出也为0,这会导致部分神经元不能表达,造成神经元死亡,降低了模型的表达能力。
为了解决ReLU函数的缺陷,引入改良的Leaky ReLU函数。
Leaky ReLU ( x ) = { x , if x > 0 α x , if x ≤ 0 \text{Leaky ReLU}(x)=\begin{cases}x,&\text{if } x>0\\\alpha x,&\text{if } x\leq0\end{cases} Leaky ReLU(x)={x,αx,if x>0if x≤0
相较ReLU函数,Leaky ReLU函数为输入小于0的部分添加了一个较小的α系数,使得输入在小于0的部分也可以表达。但是这个α超参数需要谨慎调整。
4.Softmax函数
Softmax函数将输出转换为概率分布,特别适用于多分类的任务。
S o f t m a x ( z i ) = e z i ∑ j = 1 n e z j \mathrm{Softmax}(z_i)=\frac{e^{z_i}}{\sum_{j=1}^ne^{z_j}} Softmax(zi)=∑j=1nezjezi
简单解释:首先将输出做指数运算,映射到 ( 0 , + ∞ ) (0,+\infty) (0,+∞),在对所有结果求和后对每一个结果进行归一化,映射到(0,1)之间。
由于指数运算本身属于数值放大操作,若输入值本身较大,做对数运算后可能导致数值溢出 ,因此Pytorch对函数进行了优化:
S o f t m a x ( z i ) = e z i − max ( z ) ∑ j = 1 n e z j − max ( z ) \mathrm{Softmax}(z_i)=\frac{e^{z_i-\max(z)}}{\sum_{j=1}^ne^{z_j-\max(z)}} Softmax(zi)=∑j=1nezj−max(z)ezi−max(z)
同时,由于设计较多指数运算,Softmax函数在面对大量类别时计算开销大。
5.总结
1.在隐藏层中优先选择ReLU函数作为激活函数。
2.对于输出层,多分类问题选择Softmax函数,二分类可以选择sigmoid函数。
二、参数初始化
参数初始化对于神经网络模型的训练十分关键,适当初始化参数可以使得模型的收敛速度和效果得到提升。
我们希望在所有可学习参数的层进行参数初始化。
1.固定值初始化
顾名思义,将参数初始化为固定值,但这类方法会破坏网络的对称性,导致模型无法收敛或停滞,一般不会使用。
常见API:
1.全零初始化:nn.init.zeros_(linear.weight)
2.全一初始化:nn.init.ones_(linear.weight)
3.任意值初始化:nn.init.constant_(linear.weight, 0.63)
2.随机初始化
将参数设置为一些随机值,一般从正态分布或均匀分布中取样。可以有效避免破坏模型对称性。
API:
1.正态分布初始化:nn.init.normal_(weight,mean,std)
2.均匀分布初始化:nn.init.uniform_(weight)
随机初始化解决了对称性的问题,但由于随机性,随机值过大或过小容易造成梯度爆炸和梯度消失的问题。
3.Xavier 初始化
Xavier 初始化是一种自适应的权重初始化方法,发生梯度消失或爆炸的本质是:信号在层间传播时的 "方差失控"。
Xavier 初始化的设计目标是:使每一层的输入信号方差与输出信号方差尽可能相等。一旦实现这一点,信号在正向传播时既不会被过度放大(避免后续层的信号 / 梯度过大),也不会被过度衰减(避免后续层的信号 / 梯度过小),从而从根源上抑制梯度爆炸或消失。
核心概念为:前向传播方差一致性,反向传播方差一致性。同时,Xavier 初始化对两种情况做了综合考量。
V a r ( z ) = n i n ⋅ V a r ( W ) ⋅ V a r ( x ) Var(z)=n_{in}⋅Var(W)⋅Var(x) Var(z)=nin⋅Var(W)⋅Var(x)
x n o u t ⋅ V a r ( W ) = 1 ⟹ V a r ( W ) = 1 n o u t xn_{out}⋅Var(W)=1 ⟹ Var(W)=\frac{1}{n_{out}} xnout⋅Var(W)=1 ⟹ Var(W)=nout1
API:
1.nn.init.xavier_normal_(linear.weight)
2.nn.init.xavier_uniform_(linear.weight)
4.He初始化
ReLU函数是我们常用的激活函数,但Xavier 初始化对其的效果并不好,这是由于ReLU会过滤掉输出为负数的部分,使用Xavier 初始化会导致输出信号的方差会比预期更小。
因此,He初始化对公式加入了适配值1/2。
前向方差一致性:
V a r ( z ) = 1 2 n i n ⋅ V a r ( W ) ⋅ V a r ( x ) Var(z)=\frac{1}{2}n_{in}⋅Var(W)⋅Var(x) Var(z)=21nin⋅Var(W)⋅Var(x)
反向方差一致性:
V a r ( ∂ L ∂ x ) = 1 2 n o u t ⋅ V a r ( W ) ⋅ V a r ( ∂ L ∂ z ) Var(\frac{∂L}{∂x})=\frac{1}{2}n_{out}⋅Var(W)⋅Var(\frac{∂L}{∂z}) Var(∂x∂L)=21nout⋅Var(W)⋅Var(∂z∂L)
He初始化没有单独对两种情况做统一考量,而是有:fan_in,fan_out两种模式确定优先级。
API:
1.nn.init.kaiming_normal_(linear.weight, nonlinearity="relu", mode='fan_in')
2.nn.init.kaiming_uniform_(linear.weight, nonlinearity="relu", mode='fan_out')
三、损失函数
损失函数用于衡量预测值与真实值的差异,是模型效果评估的重要指标。
1.MAE损失
MAE(Mean Absolute Error,平均绝对误差)通常也被称为 L1-Loss。
MAE = 1 n ∑ i = 1 n ∣ y i − y ^ i ∣ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - \hat{y}_i \right| MAE=n1i=1∑n∣yi−y^i∣
常常用于回归问题的损失指标。
2.MSE损失
MSE(Mean Squared Error,均方误差)通过对预测值和真实值之间的误差平方取平均值。
MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2 MSE=n1i=1∑n(yi−y^i)2
常常用于回归问题的损失指标。
3.交叉熵损失
交叉熵损失函数多用于分类问题的损失指标。
首先,我们了解信息量的概念:
信息量用于衡量一个事件所包含的信息的多少。信息量的定义基于事件发生的概率:事件发生的概率越低,其信息量越大 。
I ( x ) = − l o g P ( x ) I(x)=−logP(x) I(x)=−logP(x)
接下来,我们对信息量求期望得到信息熵。
信息熵是信息量的期望值。熵越高,表示随机变量的不确定性越大;熵越低,表示随机变量的不确定性越小。
H ( X ) = − ∑ i = 1 n P ( x i ) l o g P ( x i ) H(X)=−∑_{i=1}^n P(x_i)logP(x_i) H(X)=−i=1∑nP(xi)logP(xi)
最后,我们引入KL散度的概念:
D K L ( P ∣ ∣ Q ) = ∑ i P ( x i ) l o g P ( x i ) Q ( x i ) = ∑ i P ( x i ) [ l o g P ( x i ) − l o g Q ( x i ) ] = ∑ i P ( x i ) l o g P ( x i ) − ∑ i P ( x i ) l o g Q ( x i ) = − ( − ∑ i P ( x i ) l o g P ( x i ) ) + ( − ∑ i P ( x i ) l o g Q ( x i ) ) = − H ( P ) + ( − ∑ i P ( x i ) l o g Q ( x i ) ) = H ( P , Q ) − H ( P ) D_{KL}(P||Q)=∑_iP(x_i)log\frac{P(x_i)}{Q(x_i)}=∑_iP(x_i)[log{P(x_i)}-log{Q(x_i)}]\\ =∑_iP(x_i)log{P(x_i)}-∑_iP(x_i)log{Q(x_i)}=-(-∑_iP(x_i)log{P(x_i)})+(-∑_iP(x_i)log{Q(x_i)})\\ =-H(P)+(-∑_iP(x_i)log{Q(x_i)})\\ =H(P,Q)-H(P) DKL(P∣∣Q)=i∑P(xi)logQ(xi)P(xi)=i∑P(xi)[logP(xi)−logQ(xi)]=i∑P(xi)logP(xi)−i∑P(xi)logQ(xi)=−(−i∑P(xi)logP(xi))+(−i∑P(xi)logQ(xi))=−H(P)+(−i∑P(xi)logQ(xi))=H(P,Q)−H(P)
由上述公式可知,P是真实分布,H§是常数,所以KL散度可以用H(P,Q)来表示;H(P,Q)叫做交叉熵。
如果将P换成y,Q换成 y ^ \hat{y} y^,则交叉熵公式为:
CrossEntropyLoss ( y , y ^ ) = − ∑ i = 1 C y i log ( y ^ i ) \text{CrossEntropyLoss}(y, \hat{y}) = - \sum_{i=1}^{C} y_i \log(\hat{y}_i) CrossEntropyLoss(y,y^)=−i=1∑Cyilog(y^i)
在实际情况中,分类的输出层一般使用Softmax函数,因此最后会将Softmax的结果直接带入交叉熵损失函数。
如果是二分类问题,公式可以进一步化简为:
CELoss ( y , y ^ ) = − [ y l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ ) ] \text{CELoss}(y, \hat{y}) = -[ylog(\hat{y}) + (1-y)log(1-\hat{y})] CELoss(y,y^)=−[ylog(y^)+(1−y)log(1−y^)]
4.总结
- 多分类问题一般使用交叉熵损失函数,二分类问题一般使用二元交叉熵函数。
- 回归问题一般使用MSE,MAE。
THE END