图机器学习（11）——链接预测

图机器学习（11）------链接预测

- [0. 链接预测](#0. 链接预测)
- [1. 基于相似性的方法](#1. 基于相似性的方法)
- - [1.1 基于指标的方法](#1.1 基于指标的方法)
  - [1.2 基于社区的方法](#1.2 基于社区的方法)
- [2. 基于嵌入的方法](#2. 基于嵌入的方法)

0. 链接预测

链接预测 (link prediction)，也称为图补全，是处理图时常见的问题。具体而言，给定一个部分观测的图(即某些节点对之间是否存在边无法确定)，我们的目标是预测未知状态节点对之间是否存在边，如下图所示。

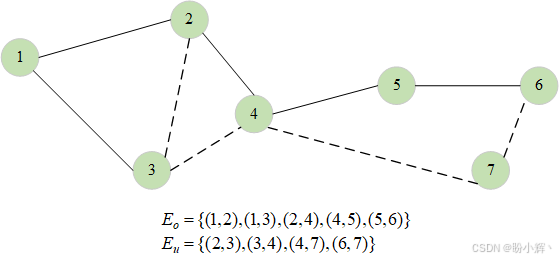
设图 G = ( V , E ) G=(V,E) G=(V,E) 的节点集为 V V V，边集为 E = E o ∪ E u E=E_o\cup E_u E=Eo∪Eu。其中，边集 E o E_o Eo 表示已知边(观测到的链接)，而边集 E u E_u Eu 表示未知边(待预测的链接)。链接预测的目标是利用 V V V 和 E o E_o Eo 的信息来估计 E u E_u Eu。该问题在时序图数据中同样常见。在此设定下，假设 G t G_t Gt 是在时间点 t t t 观测到的图，我们的目标是预测该图在时间点 t + 1 t+1 t+1 的边。

链接预测问题在各领域均有广泛应用：在社交网络中用于推荐好友关系，在电子商务平台中用于推荐商品；在生物信息学中则用于分析蛋白质相互作用。接下来，我们将介绍解决链接预测问题的两类方法------即基于相似性的方法和基于嵌入的方法。

1. 基于相似性的方法

本节介绍若干解决标签预测问题的简单算法，其核心思想是通过计算图中节点对的相似度函数来预测连接概率：若节点相似度高，则它们有较高的概率通过一条边连接。这些算法可分为两类：基于索引的方法和基于社区的方法。前者通过简单计算节点邻居关系指标得出结果，后者则使用关于节点所属社区的信息进行计算。接下来，以 networkx 库(具体模块为 networkx.algorithms.link_prediction )的标准实现为例进行演示。

1.1 基于指标的方法

本节介绍 networkx 中计算未连接节点间边概率的算法，这些算法均通过分析两节点邻居关系来构建简单指标。

资源分配指数 (resource allocation index)

该方法通过以下公式计算所有节点对的资源分配指数，进而估计节点 v v v 与 u u u 之间存在连接的概率：：
r ( u , v ) = ∑ w ∈ N ( u ) ∩ N ( v ) 1 ∣ N ( w ) ∣ r(u,v)=\sum_{w\in N(u)\cap N(v)}\frac 1{|N(w)|} r(u,v)=w∈N(u)∩N(v)∑∣N(w)∣1

在以上公式中，函数 N ( v ) N(v) N(v) 用于计算节点 v v v 的邻居集合， w w w 代表同时是 u u u 和 v v v 邻居的节点。我们可以使用 networkx 计算该指数：

python 复制代码

import networkx as nx
edges = [[1,3],[2,3],[2,4],[4,5],[5,6],[5,7]]
G = nx.from_edgelist(edges)
preds = nx.resource_allocation_index(G,[(1,2),(2,5),(3,4)])

resource_allocation_index 函数的第一个参数是输入图，第二个参数是待计算的潜在边列表。代码运行结果如下所示：

shell 复制代码

[(1, 2, 0.5), (2, 5, 0.5), (3, 4, 0.5)]

输出结果是一个包含 (1,2)、(2,5)、(3,4) 等节点对的列表及其对应的资源分配指数值。根据输出可知，这些节点对之间存在连接边的概率均为 0.5。

Jaccard 系数

该算法基于 Jaccard 系数计算节点 u u u 和 v v v 之间的连接概率：
J ( u , v ) = ∣ N ( u ) ∩ N ( v ) ∣ ∣ N ( u ) ∪ N ( v ) ∣ J(u,v)=\frac {|N(u)\cap N(v)|}{|N(u)\cup N(v)|} J(u,v)=∣N(u)∪N(v)∣∣N(u)∩N(v)∣

其中 N ( v ) N(v) N(v) 表示节点 v v v 的邻居集合。在 networkx 中可通过以下代码实现：

python 复制代码

import networkx as nx
edges = [[1,3],[2,3],[2,4],[4,5],[5,6],[5,7]]
G = nx.from_edgelist(edges)
preds = nx.resource_allocation_index(G,[(1,2),(2,5),(3,4)])

代码运行结果如下所示：

复制代码

[(1, 2, 0.5), (2, 5, 0.25), (3, 4, 0.3333333333333333)]

根据输出结果，节点 (1,2) 之间存在边的概率为 0.5，节点 (2,5) 之间为 0.25，节点 (3,4) 之间为 0.333。

除此之外，networkx 库还提供了许多其他基于相似度得分的节点连接概率计算方法，例如 nx.adamic_adar_index 和 nx.preferential_attachment，分别基于 Adamic/Adar 指数和偏好连接指数计算。这些函数的参数格式与前述方法一致，均需输入图结构和待计算的节点对列表。

1.2 基于社区的方法

与基于指标的方法类似，本类算法同样通过计算指数来评估未连接节点的连接概率。二者的核心区别在于：基于社区的方法在生成指数前，需先计算节点所属社区信息，同时基于社区的算法逻辑融合了社区拓扑特征。接下来，我们将介绍一些常见的基于社区的方法。

社区公共邻居 (community common neighbor)

为了估算两个节点连接的概率，该算法计算公共邻居的数量，并将属于同一社区的公共邻居数量加到该值中。对于两个节点 u u u 和 v v v，社区公共邻居值的计算方式如下：
c ( u , v ) = ∣ N ( u ) ∪ N ( v ) ∣ + ∑ w ∈ N ( u ) ∩ N ( v ) f ( w ) c(u,v)=|N(u)\cup N(v)|+\sum_{w\in N(u)\cap N(v)}f(w) c(u,v)=∣N(u)∪N(v)∣+w∈N(u)∩N(v)∑f(w)

其中， N ( v ) N(v) N(v) 表示节点 v v v 的邻居集合，当节点 w w w 与 u u u 属于同一社区时 f ( w ) = 1 f(w)=1 f(w)=1，否则为 0 0 0。在 networkx 中通过以下代码计算：

python 复制代码

import networkx as nx
edges = [[1,3],[2,3],[2,4],[4,5],[5,6],[5,7]]
G = nx.from_edgelist(edges)
G.nodes[1]["community"] = 0
G.nodes[2]["community"] = 0
G.nodes[3]["community"] = 0
G.nodes[4]["community"] = 1
G.nodes[5]["community"] = 1
G.nodes[6]["community"] = 1
G.nodes[7]["community"] = 1
preds = nx.cn_soundarajan_hopcroft(G,[(1,2),(2,5),(3,4)])

从上述代码中可以看到，我们需要为图中的每个节点分配社区属性 (community property)。该属性用于在计算前文定义的 f ( v ) f(v) f(v) 函数时，识别属于同一社区的节点，社区属性值也可以通过特定算法自动计算获得。cn_soundarajan_hopcroft 函数接受输入图和我们希望计算得分的节点对。代码执行结果如下所示：

shell 复制代码

[(1, 2, 2), (2, 5, 1), (3, 4, 1)]

与前述其它函数的主要区别在于指标值的范围。可以看到，该函数的输出值并不限定在 (0,1) 区间内。

社区资源分配 (community resource allocation)

与社区共同邻居算法类似，社区资源分配算法将从节点邻居处获得的信息与节点所属社区特征合并：
c ( u , v ) = ∑ w ∈ N ( u ) ∩ N ( v ) f ( w ) ∣ N ( w ) ∣ c(u,v)=\sum_{w\in N(u)\cap N(v)}\frac {f(w)}{|N(w)|} c(u,v)=w∈N(u)∩N(v)∑∣N(w)∣f(w)

其中， N ( v ) N(v) N(v) 表示节点 v v v 的邻居集合，当节点 w w w 与 u u u、 v v v 属于同一社区时 f ( w ) = 1 f(w)=1 f(w)=1，否则为 0 0 0。在 networkx 中的实现代码如下：

python 复制代码

import networkx as nx
edges = [[1,3],[2,3],[2,4],[4,5],[5,6],[5,7]]
G = nx.from_edgelist(edges)
G.nodes[1]["community"] = 0
G.nodes[2]["community"] = 0
G.nodes[3]["community"] = 0
G.nodes[4]["community"] = 1
G.nodes[5]["community"] = 1
G.nodes[6]["community"] = 1
G.nodes[7]["community"] = 1
preds = nx. ra_index_soundarajan_hopcroft(G,[(1,2),(2,5),(3,4)])

从以上代码中可以看到，我们需要为图中的每个节点分配社区属性。该属性在计算前文定义的函数时，用于识别属于同一社区的节点，这些社区值也可以通过特定的算法自动计算获得。ra_index_soundarajan_hopcroft 函数接受输入图和我们希望计算得分的节点对。代码执行结果如下所示：

shell 复制代码

[(1, 2, 0.5), (2, 5, 0), (3, 4, 0)]

从输出结果可以明显看出社区属性对指数计算的影响：同属一个社区的节点 1 和 2 获得了较高的指数值 0.5，相反，分属不同社区的节点对 (2,5) 和 (3,4) 则得分为 0。
networkx 还提供了另外两种结合社区信息的连接概率计算方法：nx.within_inter_cluster (基于集群内外连接分析)和 nx.common_neighbor_centrality (基于共同邻居中心性)。

在下一节中，我们将介绍如何结合机器学习和边嵌入 (edge embedding) 来预测未知边。

2. 基于嵌入的方法

在本节中，我们将介绍一种更先进的链路预测方法。该方法的核心理念是将链路预测问题转化为监督式分类任务。具体而言，对于给定图数据，每对节点均通过特征向量 ( x x x) 表示，并分配类别标签 ( y y y)。形式化定义为：设图 G = ( V , E ) G=(V,E) G=(V,E)，对于任意节点对 i , j i,j i,j，构建如下公式：
x = [ f 0 , 0 , . . . , f i , j , . . . , f n , n ] y = [ y 0 , 0 , . . . , y i , j , . . . , y n , n ] x=[f_{0,0},...,f_{i,j},...,f_{n,n}]\\ y=[y_{0,0},...,y_{i,j},...,y_{n,n}] x=[f0,0,...,fi,j,...,fn,n]y=[y0,0,...,yi,j,...,yn,n]

其中， f i , j ∈ x f_{i,j}\in x fi,j∈x 表示节点对 i , j i,j i,j 的特征向量， y i , j ∈ y y_{i,j}\in y yi,j∈y 为其对应标签。 y i , j y_{i,j} yi,j 的取值规则为：若图 G G G 中存在连接节点 i , j i,j i,j 的边，则 y i , j = 1 y_{i,j}=1 yi,j=1；否则 y i , j = 0 y_{i,j}=0 yi,j=0。通过特征向量和标签数据，我们可以训练机器学习算法来预测特定节点对是否可能构成图中的合理边。

虽然节点对的标签向量构建相对简单，但特征空间的构建则更具挑战性。为生成每对节点的特征向量，我们将采用嵌入技术(如 node2vec 和 edge2vec)。这些嵌入算法能显著简化特征空间的生成过程。整个流程可概括为两个核心步骤：

使用 node2vec 算法计算图 G G G 中每个节点的嵌入向量
对图中所有可能的节点对，使用 edge2vec 算法计算其嵌入表示

随后，我们可以将生成的嵌入特征向量输入通用机器学习算法来解决分类问题。为便于理解，我们通过代码示例演示完整流程(从图构建到链路预测)，数据集采用论文引用网络数据集 Cora。

(1) 首先，基于该数据集构建 networkx 图结构：

python 复制代码

import networkx as nx
import pandas as pd
from torch_geometric.utils import from_networkx

edgelist = pd.read_csv("cora.cites", sep='\t', header=None, names=["target", "source"])
G = nx.from_pandas_edgelist(edgelist)
# 将图转换为PyG格式
pyg_data = from_networkx(G)
draw_graph(G, nx.spring_layout(G))

(2) 接下来，基于图 G 创建训练集和测试集。具体而言，数据集不仅需要包含图 G 中真实边的子集，还需包含不构成真实边的节点对。真实边对应的节点对将作为正样本(类别标签 1)，而非真实边的节点对作为负样本(类别标签 0)：

python 复制代码

from sklearn.model_selection import train_test_split
import numpy as np

edges = list(G.edges())
non_edges = list(nx.non_edges(G))

train_edges, test_edges = train_test_split(edges, test_size=0.1, random_state=42)
train_non_edges, test_non_edges = train_test_split(non_edges, test_size=0.1)

# Rebuild train graph without test edges
graph_train = nx.Graph()
graph_train.add_nodes_from(G.nodes())
graph_train.add_edges_from(train_edges)

(3) 对于每个实例，需要生成它们的特征向量。在本节中，使用 node2vec 库来生成节点嵌入：

python 复制代码

from node2vec import Node2Vec
from node2vec.edges import HadamardEmbedder

node2vec = Node2Vec(graph_train)
model = node2vec.fit()
edges_embs = HadamardEmbedder(keyed_vectors=model.wv)

# Create training data
samples_train = train_edges + train_non_edges
labels_train = [1]*len(train_edges) + [0]*len(train_non_edges)
train_embeddings = [edges_embs[str(x[0]), str(x[1])] for x in samples_train]

# Create testing data
samples_test = test_edges + test_non_edges
labels_test = [1]*len(test_edges) + [0]*len(test_non_edges)
test_embeddings = [edges_embs[str(x[0]), str(x[1])] for x in samples_test]

(4) 使用 train_embeddings 特征空间和 train_labels 标签分配，最终训练机器学习算法来解决标签预测问题：

python 复制代码

from sklearn.ensemble import RandomForestClassifier
from sklearn import metrics

# Train classifier
rf = RandomForestClassifier(n_estimators=200)
rf.fit(train_embeddings, labels_train)

# Predict and evaluate
y_pred = rf.predict(test_embeddings)

print('Precision:', metrics.precision_score(labels_test, y_pred))
print('Recall:', metrics.recall_score(labels_test, y_pred))
print('F1-Score:', metrics.f1_score(labels_test, y_pred))

在本节中，使用了一个简单的 RandomForestClassifier 类，我们可以将训练好的模型应用到 test_embeddings 特征空间中，以量化分类的质量：

python 复制代码

print('Precision:', metrics.precision_score(labels_test, y_pred))
print('Recall:', metrics.recall_score(labels_test, y_pred))
print('F1-Score:', metrics.f1_score(labels_test, y_pred))

结果输出如下：

shell 复制代码

Precision:：0.8557114228456913
Recall：0.8102466793168881
F1-Score：0.8323586744639375

上述方法只是一个通用的框架，流程中的每个部分------例如训练/测试拆分、节点/边嵌入和机器学习算法------都可以根据具体问题进行修改。该方法在处理时序图的链接预测时尤为有效，此时在时间点 t t t 获取的边信息可用于训练模型，进而预测时间点 t + 1 t+1 t+1 可能出现的边。

本节我们系统阐述了链接预测问题，通过多种示例详细介绍了链接预测的不同解决方案，展示了从基于简单指标的技术到基于嵌入的复杂技术的多元解决路径。