【深度学习】神经网络 批量标准化-part6

绝顶大聪明2025-07-20 11:16

九、批量标准化

是一种广泛使用的神经网络正则化技术，对每一层的输入进行标准化，进行缩放和平移，目的是加速训练，提高模型稳定性和泛化能力，通常在全连接层或是卷积层之和，激活函数之前使用

核心思想

对每一批数据的通道进行标准化，解决内部协变量偏移

加速网络训练；运行使用更大的学习率；减少对初始化的依赖；提供轻微的正则化效果

思路：在输入上执行标准化操作，学习两可训练的参数：缩放因子γ和偏移量β

批量标准化操作 在训练阶段和测试阶段行为是不同的。测试阶段没有mini_batch数据，无法直接计算当前batch的均值和方差，所以使用训练阶段计算的全局统量（均值和方差）进行标准化

1. 训练阶段的批量标准化

1.1 计算均值和方差

对于给定的神经网络层，输入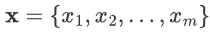，m是批次大小。我们计算该批次数据的均值和方差

均值

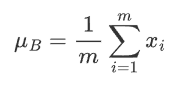
方差

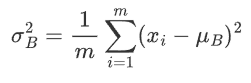
1.2 标准化

用计算得到的均值和方差对数据进行标准化，使得没个特征的均值为0，方差为1

标准化后的值

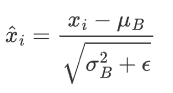
ε是很小的常数，防止除0

1.3 缩放和平移

标准化的数据通常会通过可训练的参数进行缩放和平移，以挥发模型的表达能力

缩放

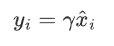
平移

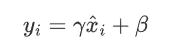
γ和β是在训练过程中学习到的参数，会随着网络的训练过程通过反向传播进行更新

1.4 更新全局统计量

指数移动平均更新全局均值和方差

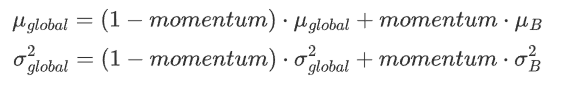
momentum是超变量，控制当前mini-batch统计量对全局统计量的贡献

它在0到1之间，控制mini-batch统计量的权重，在pytorch默认为0.1

与优化器中的momentum的区别

标准化中的：

更新全局统计量

控制当前mini-batch统计量对全局统计量的贡献

优化器中：

加速梯度下降，跳出局部最优

2.测试阶段的批量标准化

测试阶段没有mini-batch数据，所以通过EMA计算的全局统计量来进行标准化

测试阶段用全局统计量对输入数据进行标准化

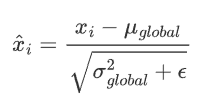
对标准化后的数据进行缩放和平移

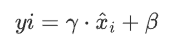
为什么用全局统计量

一致性：

  • 在测试 阶段，输入数据通常是单个样本或少量样本 ，无法准确计算均值和方差。

  • 使用全局统计量可以确保测试阶段的行为与训练阶段一致。

稳定性：

  • 全局统计量是通过训练阶段的大量 mini-batch 数据计算得到的，能够更好地反映数据的整体分布。

  • 使用全局统计量可以减少测试阶段的随机性 ，使模型的输出更加稳定。

效率：

  • 在测试阶段，使用预先计算的全局统计量可以避免重复计算，提高效率。

3. 作用

3.1 缓解梯度问题

防止激活值过大或过小，避免激活函数的饱和，缓解梯度消失或爆炸

3.2 加速训练

输入值分布更稳定，提高学习训练的效率，加速收敛

3.3 减少过拟合

类似于正则化，有助于提高模型的泛化能力

避免对单一数据点的过度拟合

4. 函数说明

torch.nn.BatchNorm1d 是 PyTorch 中用于一维数据的批量标准化（Batch Normalization）模块。

复制代码 
torch.nn.BatchNorm1d(
    num_features,         # 输入数据的特征维度
    eps=1e-05,           # 用于数值稳定性的小常数
    momentum=0.1,        # 用于计算全局统计量的动量
    affine=True,         # 是否启用可学习的缩放和平移参数
    track_running_stats=True,  # 是否跟踪全局统计量
    device=None,         # 设备类型（如 CPU 或 GPU）
    dtype=None           # 数据类型
)

参数说明：

eps：用于数值稳定性的小常数 ，添加到方差的分母中，**防止除零错误。**默认值：1e-05

momentum：用于计算全局统计量 （均值和方差）的动量 。默认值：0.1，参考本节1.4

affine：是否启用可学习的缩放和平移参数（γ和 β）。如果 affine=True ，则模块会学习两个参数；如果 affine=False，则不学习参数 ，直接输出标准化后的值 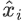。默认值：True

track_running_stats：是否跟踪全局统计量（均值和方差）。如果 track_running_stats=True，则在训练过程中计算并更新全局统计量，并在测试阶段使用这些统计量。如果 track_running_stats=False，则不跟踪全局统计量，每次标准化都使用当前 mini-batch 的统计量。默认值：True

4. 代码实现

复制代码 
import torch
from torch import nn
from matplotlib import pyplot as plt

from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from torch.nn import functional as F
from torch import optim

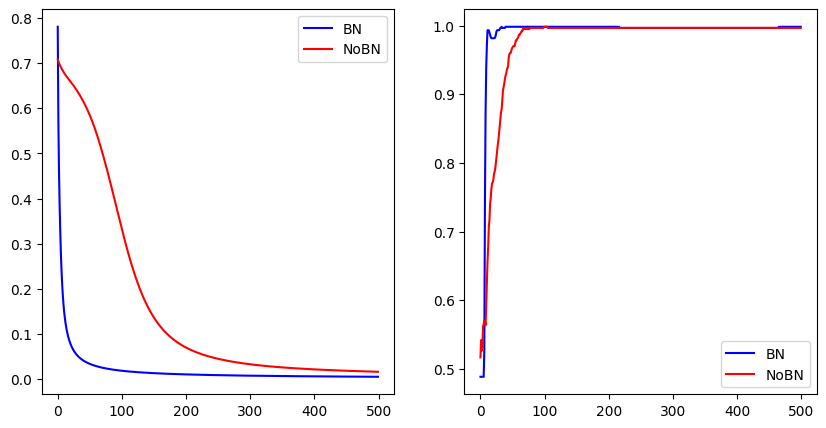
# 生成数据集：两个同心圆，内圈和外圈的点分别属于两个类别
x, y = make_circles(n_samples=2000, noise=0.1, factor=0.4, random_state=42)
# 转换为PyTorch张量
x = torch.tensor(x, dtype=torch.float32)
y = torch.tensor(y, dtype=torch.long)

# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3,
                                                    random_state=42)

# 可视化数据集
plt.scatter(x[:, 0], x[:, 1], c=y, cmap='coolwarm', edgecolors="k")
plt.show()


# 定义带批量归一化的神经网络
class NetWithBN(nn.Module):
    def __init__(self):
        super().__init__()
        # 第一层全连接层，输入维度2，输出维度64
        self.fc1 = nn.Linear(2, 64)
        # 第一层批量归一化
        self.bn1 = nn.BatchNorm1d(64)
        # 第二层全连接层，输入维度64，输出维度32
        self.fc2 = nn.Linear(64, 32)
        # 第二层批量归一化
        self.bn2 = nn.BatchNorm1d(32)
        # 第三层全连接层，输入维度32，输出维度2（两个类别）
        self.fc3 = nn.Linear(32, 2)

    def forward(self, x):
        # 前向传播：ReLU激活函数+批量归一化+全连接层
        x = F.relu(self.bn1(self.fc1(x)))
        x = F.relu(self.bn2(self.fc2(x)))
        x = self.fc3(x)
        return x


# 定义不带批量归一化的神经网络
class NetWithoutBN(nn.Module):
    def __init__(self):
        super().__init__()
        # 第一层全连接层，输入维度2，输出维度64
        self.fc1 = nn.Linear(2, 64)
        # 第二层全连接层，输入维度64，输出维度32
        self.fc2 = nn.Linear(64, 32)
        # 第三层全连接层，输入维度32，输出维度2（两个类别）
        self.fc3 = nn.Linear(32, 2)

    def forward(self, x):
        # 前向传播：ReLU激活函数+全连接层
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x


# 定义训练函数
def train(model, x_train, y_train, x_test, y_test, name, lr=0.1, epoches=500):
    # 定义交叉熵损失函数
    criterion = nn.CrossEntropyLoss()
    # 定义SGD优化器
    optimizer = optim.SGD(model.parameters(), lr=lr)

    # 用于记录训练损失和测试准确率
    train_loss = []
    test_acc = []

    for epoch in range(epoches):
        # 设置模型为训练模式
        model.train()
        # 前向传播
        y_pred = model(x_train)
        # 计算损失
        loss = criterion(y_pred, y_train)
        # 反向传播
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        # 记录训练损失
        train_loss.append(loss.item())

        # 设置模型为评估模式
        model.eval()
        # 禁用梯度计算
        with torch.no_grad():
            # 前向传播
            y_test_pred = model(x_test)
            # 获取预测类别
            _, pred = torch.max(y_test_pred, dim=1)
            # 计算正确预测的数量
            correct = (pred == y_test).sum().item()
            # 计算测试准确率
            test_acc.append(correct / len(y_test))

        # 每100个epoch打印一次日志
        if epoch % 100 == 0:
            print(F"{name}|Epoch:{epoch},loss:{loss.item():.4f},acc:{test_acc[-1]:.4f}")
    return train_loss, test_acc


# 创建带批量归一化的模型
model_bn = NetWithBN()
# 创建不带批量归一化的模型
model_nobn = NetWithoutBN()

# 训练带批量归一化的模型
bn_train_loss, bn_test_acc = train(model_bn, x_train, y_train, x_test, y_test,
                                   name="BN")
# 训练不带批量归一化的模型
nobn_train_loss, nobn_test_acc = train(model_nobn, x_train, y_train, x_test, y_test,
                                       name="NoBN")


# 定义绘图函数
def plot(bn_train_loss, nobn_train_loss, bn_test_acc, nobn_test_acc):
    # 创建绘图窗口
    fig = plt.figure(figsize=(10, 5))
    # 添加子图1：训练损失
    ax1 = fig.add_subplot(1, 2, 1)
    ax1.plot(bn_train_loss, "b", label="BN")
    ax1.plot(nobn_train_loss, "r", label="NoBN")
    ax1.legend()

    # 添加子图2：测试准确率
    ax2 = fig.add_subplot(1, 2, 2)
    ax2.plot(bn_test_acc, "b", label="BN")
    ax2.plot(nobn_test_acc, "r", label="NoBN")
    ax2.legend()
    # 显示图像
    plt.show()


# 调用绘图函数
plot(bn_train_loss, nobn_train_loss, bn_test_acc, nobn_test_acc)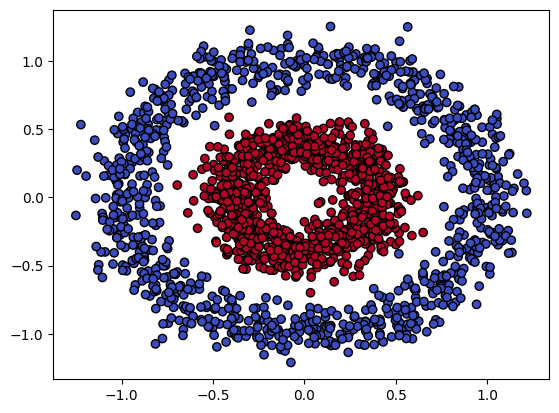

十、模型的保存和加载

1.标准网络模型构建

复制代码 
class MyModel(nn.Module):
    def __init__(self,input_size,output_size):
        super(MyModel,self).__init__()
        self.fc1 = nn.Linear(input_size,128)
        self.fc2 = nn.Linear(128,64)
        self.fc3 = nn.Linear(64,output_size)
    
    def forward(self,x):
        x = self.fc1(x)
        x = self.fc2(x)
        output = self.fc3(x)
        return output

model = MyModel(input_size=10,output_size = 2)
x  =torch.randn(5,10)

output = model(x)

2. 序列化模型对象

模型保存：

复制代码 
torch.save(obj, f, pickle_module=pickle, pickle_protocol=DEFAULT_PROTOCOL, _use_new_zipfile_serialization=True)

参数说明：

  • obj：要保存的对象，可以是模型、张量、字典等。

  • f：保存文件的路径或文件对象。可以是字符串（文件路径）或文件描述符。

  • pickle_module：用于序列化的模块，默认是 Python 的 pickle 模块。

  • pickle_protocol：pickle 模块的协议版本，默认是 DEFAULT_PROTOCOL（通常是最高版本）。

模型加载：

复制代码 
torch.load(f, map_location=None, pickle_module=pickle, **pickle_load_args)

参数说明：

  • f：文件路径或文件对象。可以是字符串（文件路径）或文件描述符。

  • map_location：指定加载对象的设备位置（如 CPU 或 GPU）。默认是 None，表示保持原始设备位置。例如：map_location=torch.device('cpu') 将对象加载到 CPU。

  • pickle_module：用于反序列化的模块，默认是 Python 的 pickle 模块。

  • pickle_load_args：传递给 pickle_module.load() 的额外参数。

    import torch
    import torch.nn as nn
    import pickle

    class MyModel(nn.Module):
    def init(self,input_size,output_size):
    super(MyModel,self).init()
    self.fc1 = nn.Linear(input_size,output_size,128)
    self.fc2 = nn.Linear(128,64)
    self.fc3 = nn.Linear(64,output_size)

    复制代码 
      def forward(self,x):
      x = self.fc1(x)
      x = self.fc2(x)
      output = self.fc3(x)
      return output

    def test001():
    model = MyModel(input_size=128,output_size=32)
    torch.save(model,"model.pkl",pickle_module=pickle,pickle_protocol=2)

    def test002():
    model = torch.load("model.pkl",map_location = "cpu",pickle_module=pickle)
    print(model)

    test001()
    test002()

.pkl是二进制文件，内容是通过pickle模块化序列的python对象。可能存在兼容问题（python2，3的区别）

.pth是二进制文件，序列化的pytorch模型或张量。

3. 模型保存参数

复制代码 
import torch
import torch.nn as nn
import torch.optim as optim
import pickle

class MyModle(nn.Module):
    def __init__(self,input_size,output_size):
        super(MyModle,self).__init__()
        self.fc1 = nn.Linear(input_size,128)
        self.fc2 = nn.Linear(128,64)
        self.fc3 = nn.Linear(64,output_size)

    def forward(self,x):
        x = self.fc1(x)
        x = self.fc2(x)
        output = self.fc3(x)
        return output
    
def test003():
    model = MyModle(input_size=128,output_size=32)
    optimizer = optim.SGD(model.parameters(),lr = 0.01)
    save_dict = {
        "init_params":{
        "input_size":128,
        "output_size":32,
        },
        "accuracy":0.99,
        "model_state_dict":model.state_dict(),
        "optimizer_state_dict":optimizer.state_dict(),
        }
    torch.save(save_dict,"model_dict.pth")

def test004():
    save_dict = torch.load("model_dict.pth")
    model = MyModle(
        input_size = save_dict["init_params"]["input_size"],
        output_size = save_dict["init_params"]["output_size"],
    )

    model.load_state_dict(save_dict["model_state_dict"])
    optimizer = optim.SGD(model.parameters(),lr = 0.01)
    optimizer.load_state_dict(save_dict["optimizer_state_dict"])
    print(save_dict["accuracy"])
    print(model)

test003()
test004()

推理时加载模型参数简单如下：

复制代码 
# 保存模型状态字典
torch.save(model.state_dict(), 'model.pth')
​
# 加载模型状态字典
model = MyModel(128, 32)
model.load_state_dict(torch.load('model.pth'))
​

十一、项目实战

相关推荐
aneasystone本尊5 分钟前
学习 RAGFlow 的知识库配置
人工智能
钟屿6 分钟前
Deep Multi-scale Convolutional Neural Network for Dynamic Scene Deblurring 论文阅读
论文阅读·人工智能·计算机视觉
aneasystone本尊11 分钟前
学习 RAGFlow 的文件上传逻辑
人工智能
洋流33 分钟前
0基础进大厂，第13天：AI-ReAct——思维链式调用API
人工智能·python
Hello server37 分钟前
混沌趋势指标原理及交易展示
人工智能·股票分析·合约交易·btc合约·eth趋势分析
Sui_Network1 小时前
Swarm Network 选择 Walrus 实现可验证 AI
人工智能·物联网·web3·区块链·量子计算
吕永强2 小时前
计算机视觉：AI 的 “眼睛” 如何看懂世界？
人工智能·科普
leafpipi2 小时前
【机器学习】安装Jupyter及基本操作
人工智能·机器学习·jupyter
伊织code2 小时前
OpenCV 官翻5 - 机器学习
人工智能·opencv·机器学习·聚类·svm·knn·k-means
黑巧克力可减脂2 小时前
大语言模型：高考志愿填报的“新纪元智能参谋”
人工智能·语言模型·高考
热门推荐
01全球最强模型Grok4，国内已可免费使用！（附教程）02Cursor Claude 模型无法使用的解决方法03KGG转MP3工具|非KGM文件|解密音频04【2025.7.18】更新vscode后所有.vue文件template标签后报红的临时解决办法，Vue - Official 插件3.0.2导致05集群聊天服务器---MySQL数据库的建立06【无标题】07Claude Code 最新版已经支持 Windows 安装使用！08身弱武修法：玄之又玄，奇妙之门09使用Ruby接入实时行情API教程102024电赛H题参考方案（+视频演示）——自动行使小车