马拉车（Manacher）算法

一、什么是马拉车（Manacher）算法

马拉车（Manacher）算法是一种高效求解字符串中最长回文子串 的算法，由 Glenn Manacher 于 1975 年提出。它的核心优势是将时间复杂度优化到了线性 O (n)（n 为字符串长度），解决了传统方法（如中心扩展法）在处理回文时的效率问题。

二、为什么需要马拉车算法？

回文子串是指正反读完全一致的子串（如 "abcba""abba"）。传统方法中，中心扩展法需要分别处理奇数长度和偶数长度的回文，且最坏时间复杂度为 O (n²)；而马拉车算法通过统一奇偶数回文的处理方式 和利用回文对称性减少重复计算，实现了线性效率。

三、如何实现？

1.预处理

首先对S做一个变换以简化问题。

在S的每个字符左右插入一个不属于S的字符,如'#'。

把

cpp 复制代码

"abcba"

变成了

cpp 复制代码

"#a#b#c#b#a#"

中心字符为'c'变换后中心字符为'#'。经过这样的变换,字符串S的新长度都是奇数,中心字符都只有一个。为了编程方便,在S的首尾再加上两个奇怪字符防止越界,如把"#a#b#b#a#"的首尾分别加上' $'和'\&"变成"$ #a#b#b#a#&"。经过变换后的字符串,不影响对其中回文串的认定

2.中心扩展法

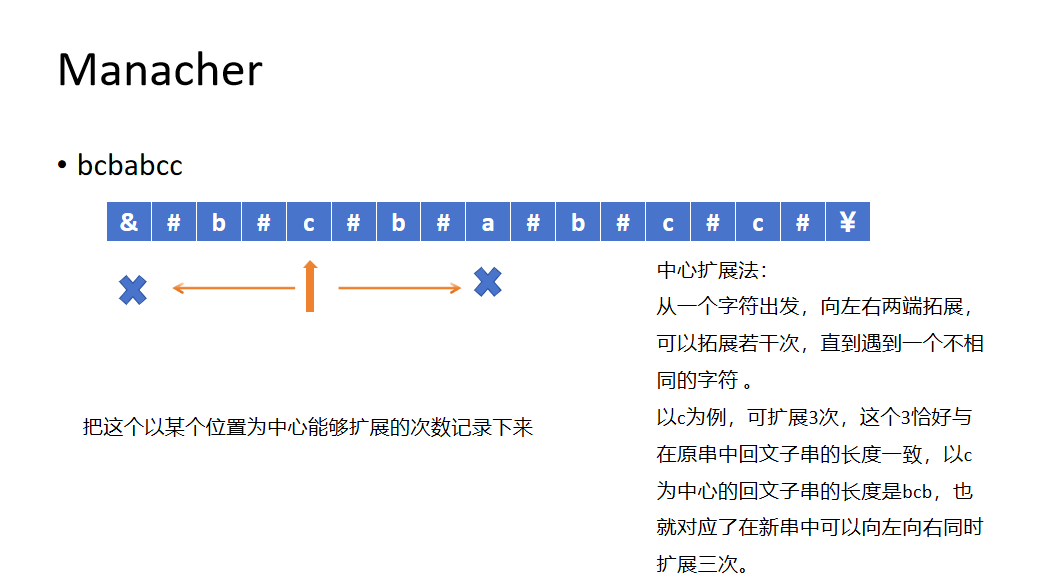
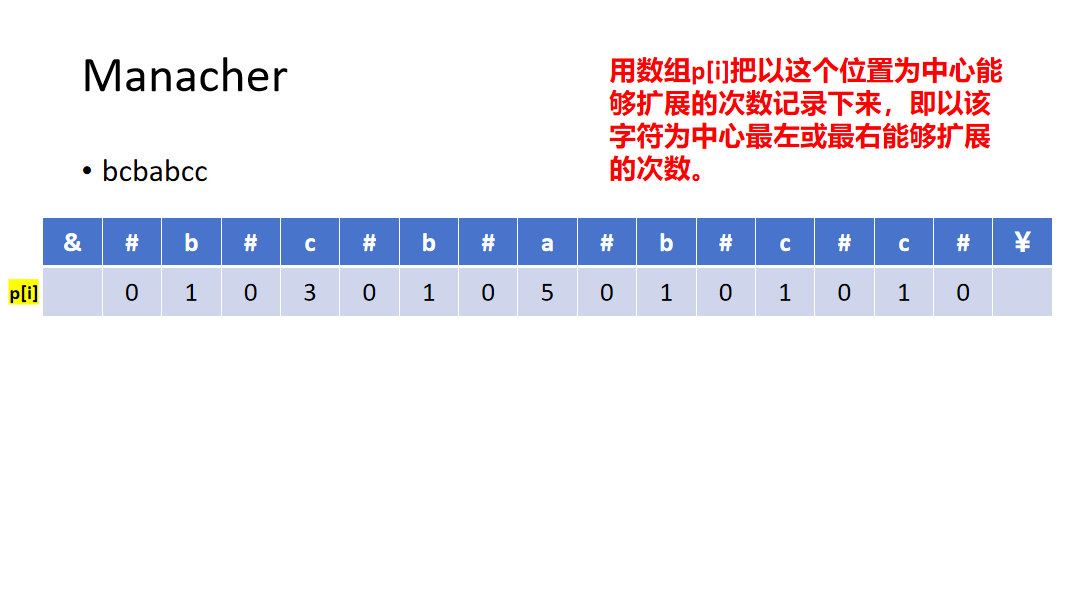
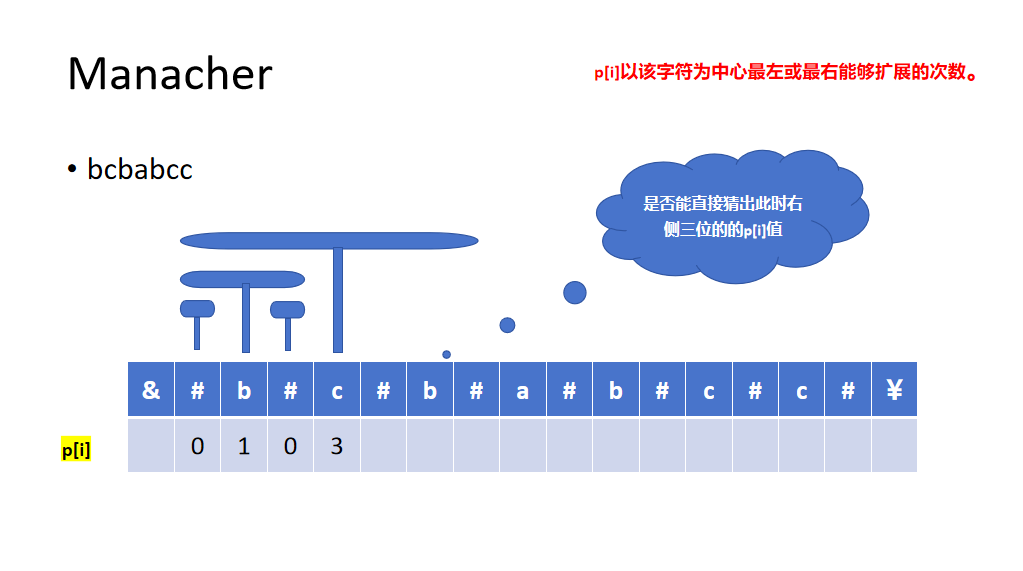
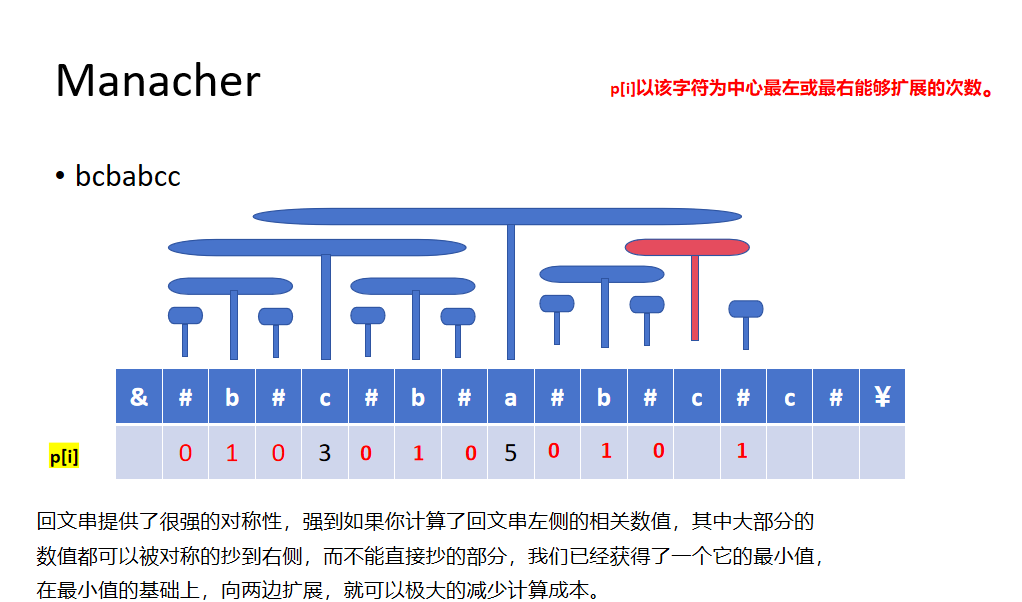
例题

https://www.luogu.com.cn/problem/P3805

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
int n;

int read(){
    int s=0,fl=1;char w=getchar();
    while(w>'9'||w<'0'){if(w=='-')fl=-1;w=getchar();}
    while(w<='9'&&w>='0'){s=s*10+(w^48);w=getchar();}
    return fl*s;
}
string s;
int main(){
    cin>>s;//输入字符串
    string T="^";
    for(char c:s){
    	T+="#";
    	T+=c;
	}//初始化添加标识符
    //R
    //含义：当前已知最右回文子串的右边界（R = C + P[C] - 1）。
    //作用：判断 i 是否在已知回文范围内，从而利用对称性优化计算。




	T+="#$";
	int n=T.size();
	vector<int> P(n,0);
	int C=0,R=0;
	for(int i=1;i<n-1;i++){
		int ii=2*C-i;//计算i关于回文中心的对称点
		if(R>i){//i 是在枚举预处理后字符串 T 的每个字符位置
                    //i<R证明i位于已知回文的范围内，可以对称过去

//P[ii] 表示对称点 ii 的回文半径。
//R - i 表示从 i 到已知回文右边界 R 的距离。
//结论：由于对称性，i 的回文半径至少为 P[ii]，且不会超过 R - i（否则会超出已知回文范围）

			P[i]=min(R-i,P[ii]);
		}
		while(T[i+P[i]+1]==T[i-P[i]-1]){
			P[i]++;
		}//两边尝试扩展长度
		
		if(i+P[i]>R){
			C=i;
			R=i+P[i];
		}
	}//更新C和R的值
	
	int macn=0;
	for(int i=1;i<n-1;i++){
		macn=max(macn,P[i]);
	}
	cout<<macn;
    return 0;
}