Java 二叉树

文章目录

• 二叉树
• • 完全二叉树和满二叉树
  • 二叉树中的性质
  • 链式存储和顺序存储
  • • 链式存储
    • 整棵树第k层的节点个数
    • 整棵树的高度
    • 查找值为val的节点
    • 面试题
    • 层序遍历
    • 判断是不是一颗完全二叉树
    • 利用非递归遍历二叉树
    • • 前序遍历
      • 中序遍历
      • 后序遍历

二叉树

1. 重点概念：节点的度，树的度，叶子节点，双亲节点，孩子节点，根节点，节点的层次，树的高度或深度

完全二叉树和满二叉树

1. 满二叉树：每层节点都打满，有k层，节点总数为2^k - 1个节点
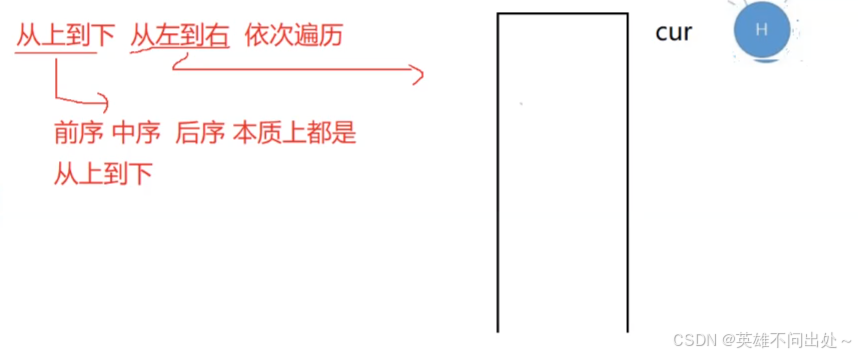
2. 完全二叉树：从上到下，从左到右，节点依次存放，中减不能有位置空节点

二叉树中的性质

1. 每层最多有2^i - 1个节点

2. 二叉树最多有2^n - 1个节点

3. 度为0的节点个数始终比度为2的节点个数多一个

   N为总节点个数，n0，n1，n2都是度为0，1，2的节点个数

   N个节点的二叉树有N-1条边

   推导：N = n0 + n1 + n2

   N - 1 = n1 + 2 * n2

   n0 = n2 + 1

4. 有n个节点的完全二叉树，有k层，那么k是多少？

   2 ^ k - 1 = n，k = log2(n + 1)

5. 已知父亲节点的下标为i

   那么左孩子下标为：2 * i + 1

   右孩子下标为：2*i + 2

已知孩子节点下标为i

那么父亲节点下标为：(i - 1) / 2

链式存储和顺序存储

链式存储

1. 孩子表示法

2. 孩子双亲表示法：可以知道孩子的父亲是谁

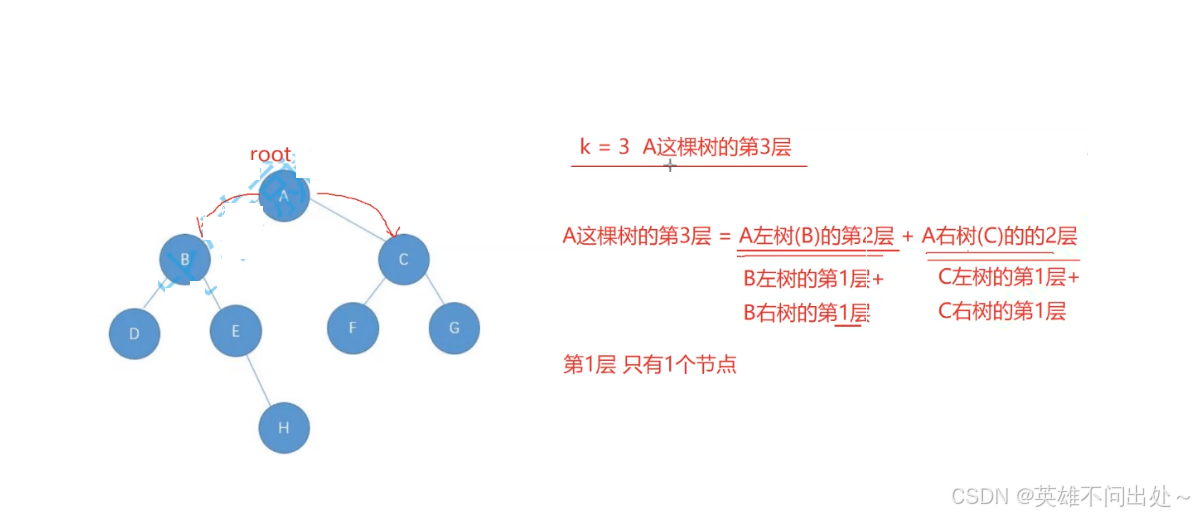
整棵树第k层的节点个数

1. 整棵树第k层的节点个数 = 这棵树左树的第k-1层节点个数 + 这棵树右树的第k-1层节点个数
   

    // 获取第k层节点的个数
    // 整棵树的第k层节点个数等于左树的第k-1层+右树的k-1层节点个数
    // 比如第3层节点个数 = 左树第2层节点 + 右树第2层节点
    public int getKLevelNodeCount(TreeNode root,int k){
        if(root == null){
            return 0;
        }
        if(k == 1){
            return 1;
        }

        int leftSize = getKLevelNodeCount(root.left,k-1);
        int rightSize = getKLevelNodeCount(root.right,k - 1);

        return leftSize + rightSize;
    }

整棵树的高度

1. 整棵树的高度 = 左子树的高度和右子树的高度，高的那个加1
2. 下面两种都是O(N)的时间复杂度，因为要把树都遍历一遍

	// 获取二叉树的高度
    public int getHigh(TreeNode root){
        if(root == null){
            return 0;
        }

        int leftHigh = getHigh(root.left);
        int rightHigh = getHigh(root.right);

        return max(leftHigh,rightHigh) + 1;
    }

    这种会超时在leetcode上,因为比完一遍大小,又要在二选一
    中继续算一遍高度
	// 获取二叉树的高度
    public int getHigh(TreeNode root){
        if(root == null){
            return 0;
        }
        
        // return max(getHigh(root.left),getHigh(root.right)) + 1;
        return getHigh(root.left) > getHigh(root.right) ?
               getHigh(root.left) + 1 : getHigh(root.right) + 1;
    }

查找值为val的节点

1. 判断是否为空树
2. 再判断根是不是val
3. 再找左子树
4. 最后找右子树

	// 查找值为val的节点
    public TreeNode find(TreeNode root,char val){
        if(root == null){
            return null;
        }

        if(root.val == val){
            return root;
        }
        TreeNode leftVal = find(root.left,val);
        // 不为空说明找到了,如果这里写leftVal.val == val
        // 会造成空指针异常,leftVal可能为空指针
        if(leftVal != null){
            return leftVal;
        }
        TreeNode rightVal = find(root.right,val);
        if(rightVal != null){
            return rightVal;
        }

        return null;
    }

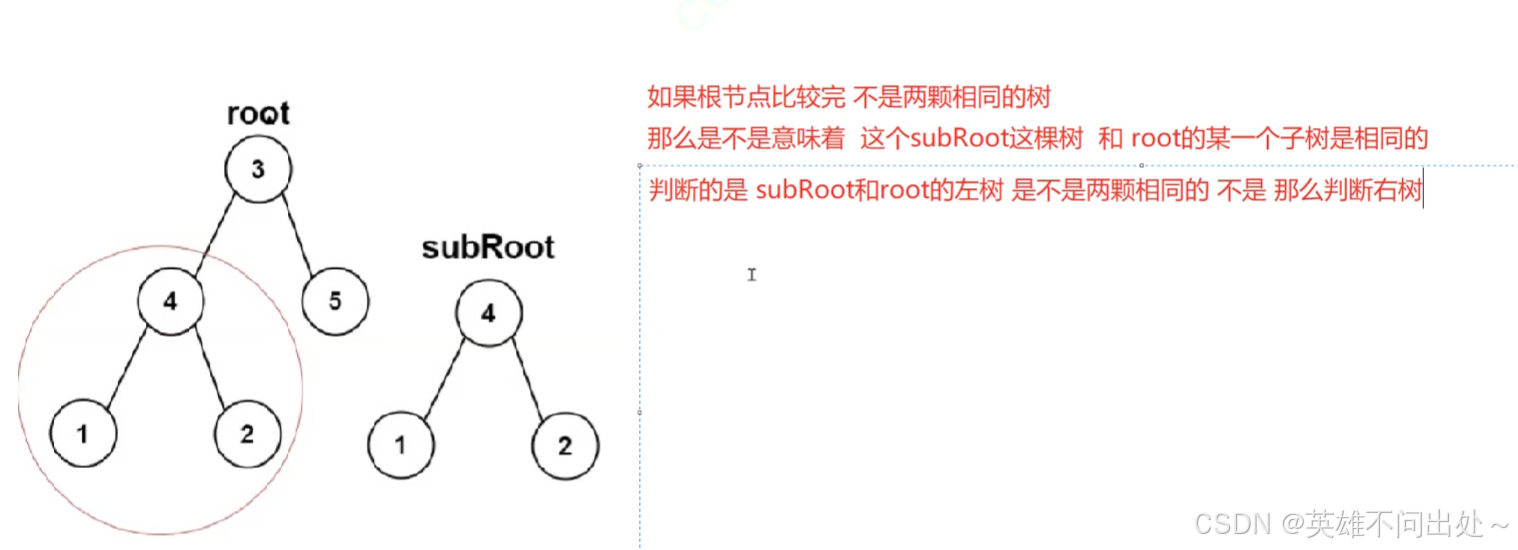
面试题

二叉树的最大深度
相同的树

时间复杂度：O(min(M，N))

两棵树中小的那个，因为有可能提前结束

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p == null && q != null){
            return false;
        }
        if(p != null && q == null){
            return false;
        }
        if(p == null && q == null){
            return true;
        }
        if(p.val != q.val){
            return false;
        }
        
        // 错误写法,为什么错?
        // 因为即使p和q结构相同并且值相同,但是后面有可能有不同的
        // 不能直接返回true
        // null直接返回true是因为它这棵树只有null自己了
        /*if(p != null && q != null){
            if(p.val == q.val){
                return true;
            }else{
                return false;
            }
        }*/

        // p != null && q != null && p.val == q.val

        boolean ret1 = isSameTree(p.left,q.left);
        boolean ret2 = isSameTree(p.right,q.right);

        return ret1 && ret2; 
    }
}

另一颗子树

翻转二叉树

平衡二叉树

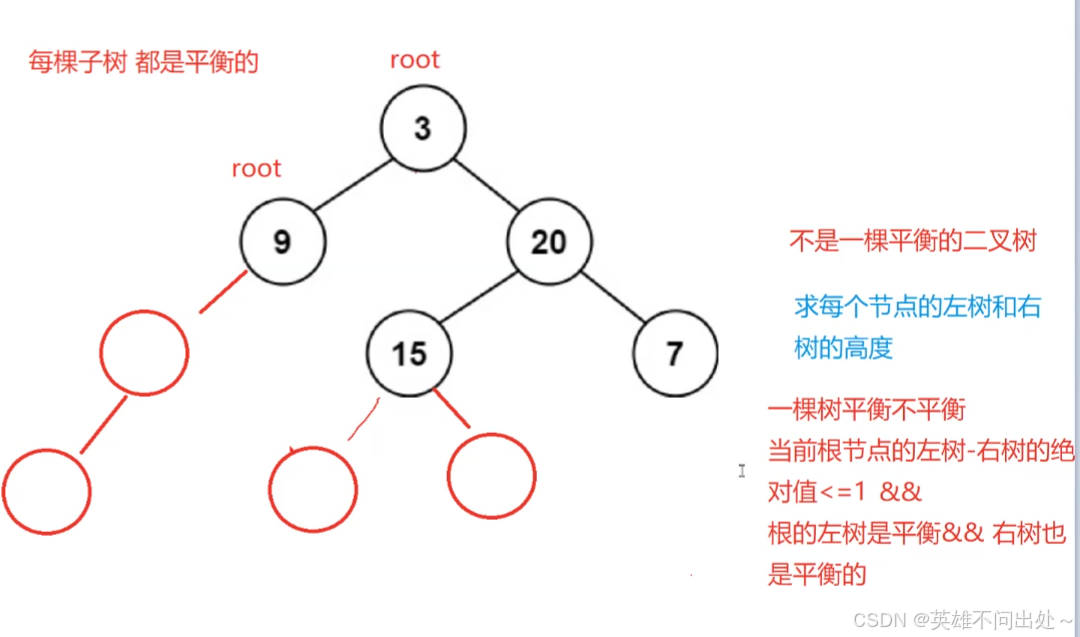
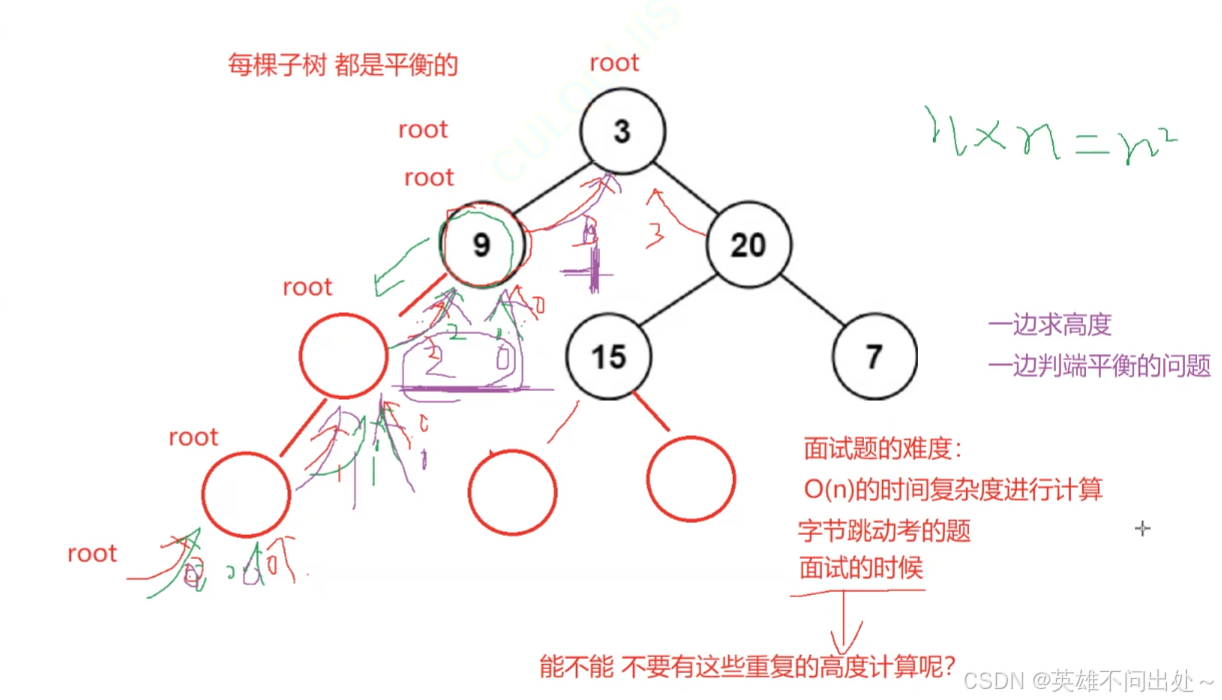
要求时间复杂度是O(N)的写法，一边求高度，一边判断是否平衡 ，如果不是平衡二叉树，跑一遍就能判断是否是平衡二叉树

class Solution {
    public boolean isBalanced(TreeNode root) {
        // 当前根节点左树和右树的高度之差的绝对值 <= 1
        // 并且左子树是平衡的,右子树也是平衡的
        
        // 时间复杂度:O(N^2)
        // 因为isBalanced相当于前序遍历,这个代码中间求高度
        // 求高度又是O(N),求高度要把每个节点都遍历一遍
        // 两者是嵌套的关系,时间复杂度就是O(N^2)

        if(root == null){
            return true;
        }

        // leftHigh - rightHigh <= 1
        return maxDepth(root) >= 0;
    }
    
    // 这次时间复杂度为O(N),只需要走求高度的这个代码
    public int maxDepth(TreeNode root) {
       if(root == null){
        return 0;
       }

       int leftHigh = maxDepth(root.left);
       // 如果左树是-1,那么不需要走右树,是不平衡的
       if(leftHigh < 0){
        return -1;
       }
       int rightHigh = maxDepth(root.right);
       
       // 只要不平衡就返回-1
       if(leftHigh >= 0 && rightHigh >= 0 &&
       Math.abs(leftHigh - rightHigh) <= 1){
            return Math.max(leftHigh,rightHigh) + 1;
       }else{
        return -1;
       }
    }
}

对称二叉树

二叉树的遍历

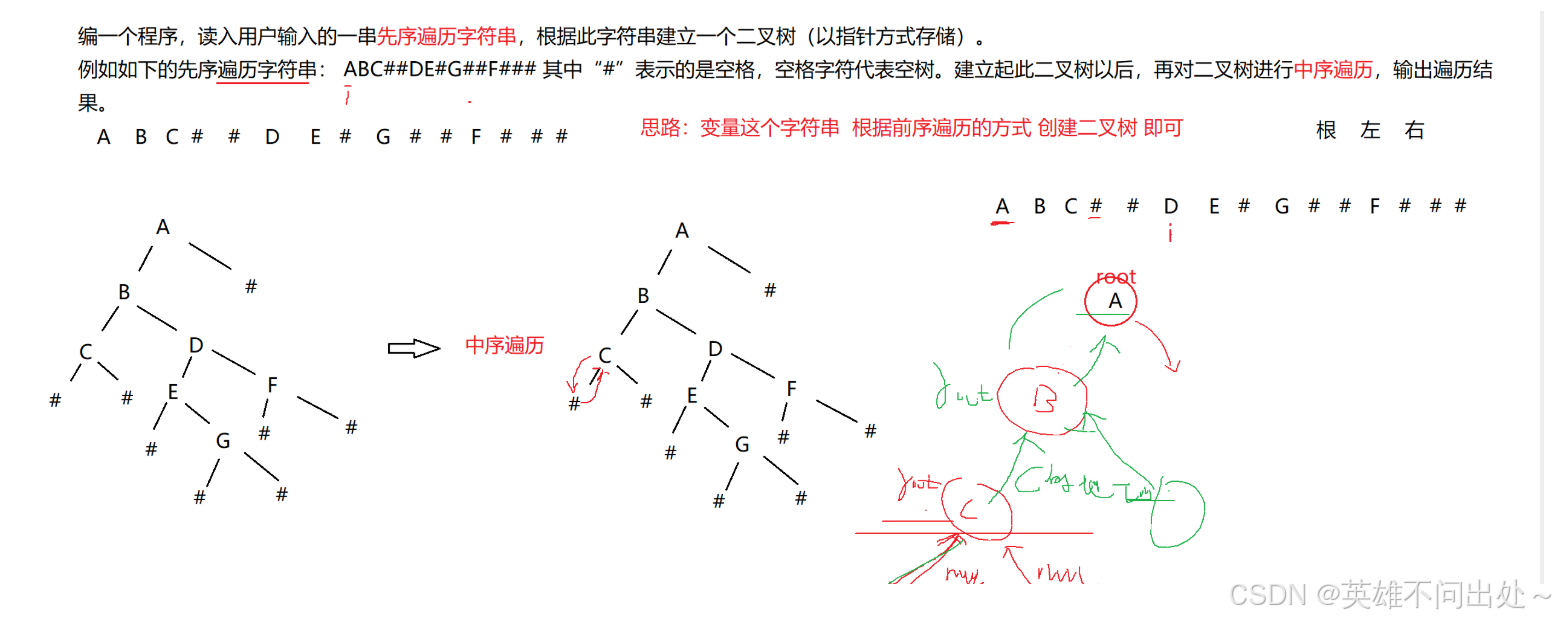
二叉树的前序遍历去构建

import java.util.Scanner;

// Java中只能有一个public的类(主类)
class TreeNode{
    public char val;
    
    public TreeNode left;
    public TreeNode right;

    public TreeNode(char val){
        this.val = val;
    }
}


// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static int i = 0;

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        // 注意 hasNext 和 hasNextLine 的区别
        while (in.hasNextLine()) { // 可以把空格也读取
           String str = in.nextLine();
           TreeNode root = createTree(str);

            inorder(root);   
        }
    }

    public static TreeNode createTree(String str){
            // 在回的时候创建二叉树的关系
            // 在回的时候连接起节点

            // 1.遍历字符串
            /*int i = 0;
            for(i = 0;i < str.length();i++){
                
            }*/
            
            TreeNode root = null;
            if(str.charAt(i) != '#'){
                // 2.利用前序遍历创建二叉树
                root = new TreeNode(str.charAt(i));
                i++;
                root.left = createTree(str);
                root.right = createTree(str);
            }else{
                i++;
            }

            // 3.#怎么处理?
            // 返回根节点

            return root;
    }

    public static void inorder(TreeNode root){
        if(root == null){
            return;
        }

        inorder(root.left);
        System.out.print(root.val + " ");
        inorder(root.right);
    }
}

二叉树的层序遍历
主要考察二维数组存储的问题

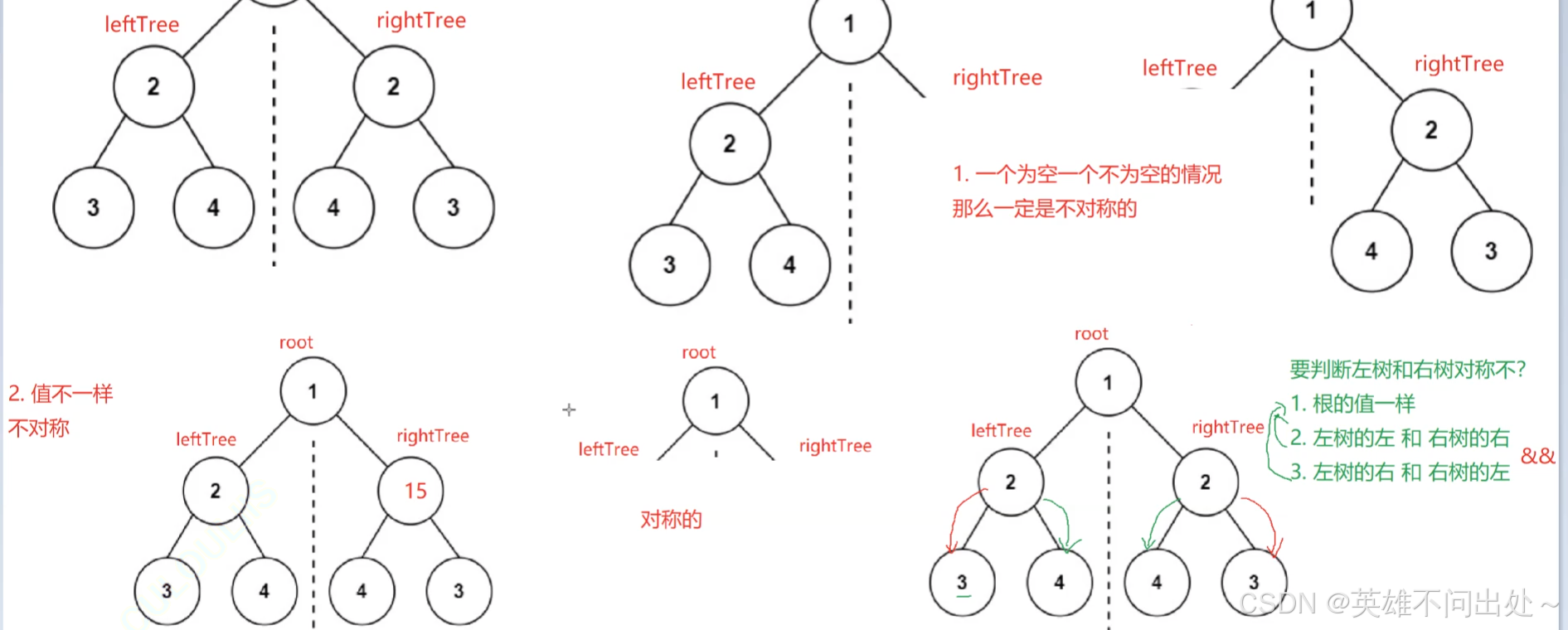
二叉树的公共祖先
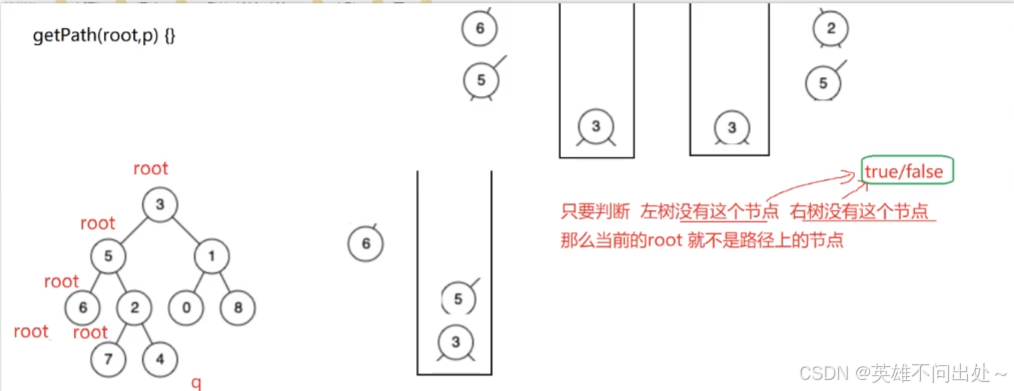
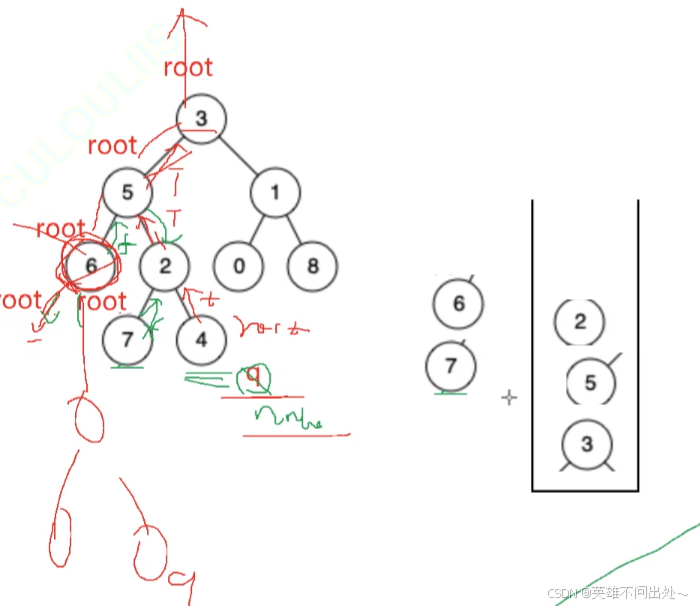
解法一：

1. 如果左树和右树都有节点，那么根节点是最近的公共祖先
2. 如果左树为空，右树不为空，那么右树第一个遇到的节点就是公共祖先
3. 如果右树为空，左树不为空，那么左树第一个遇到的节点即使公共祖先
4. 如果左树为空，右树两个节点是兄弟节点，那么他们的父节点是最近公共祖先

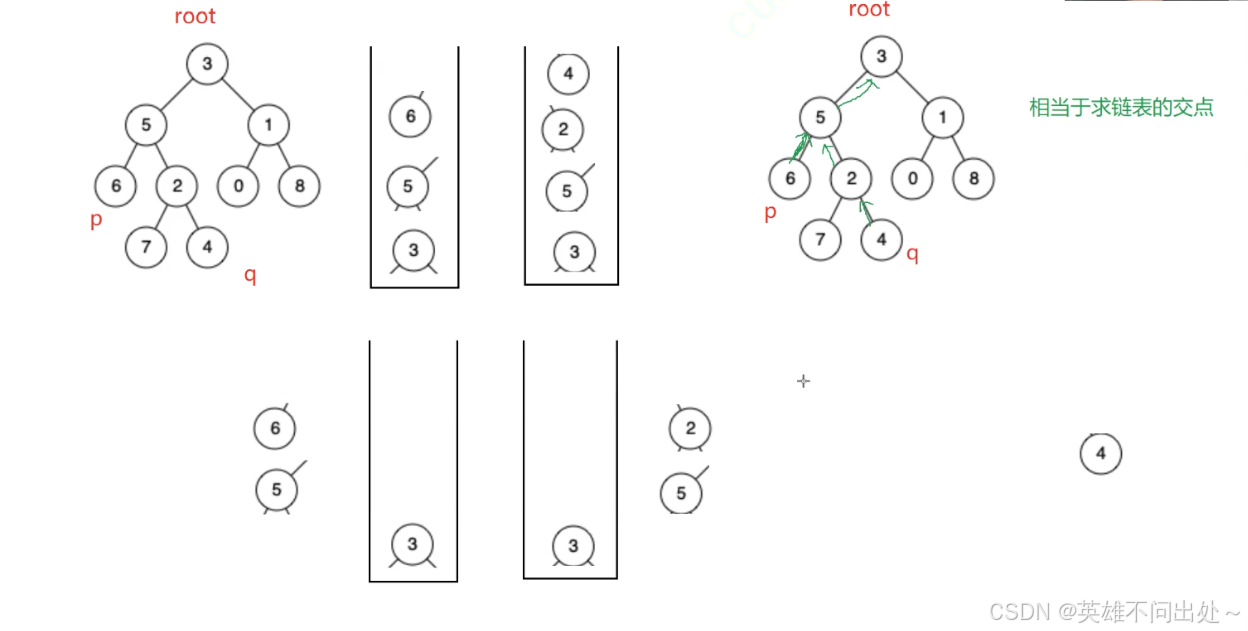
解法二：

1. 先找到p和q节点，找到p和q路径上的所有节点，在栈中先出差值个节点，再同时出节点，如果节点一样就是公共节点

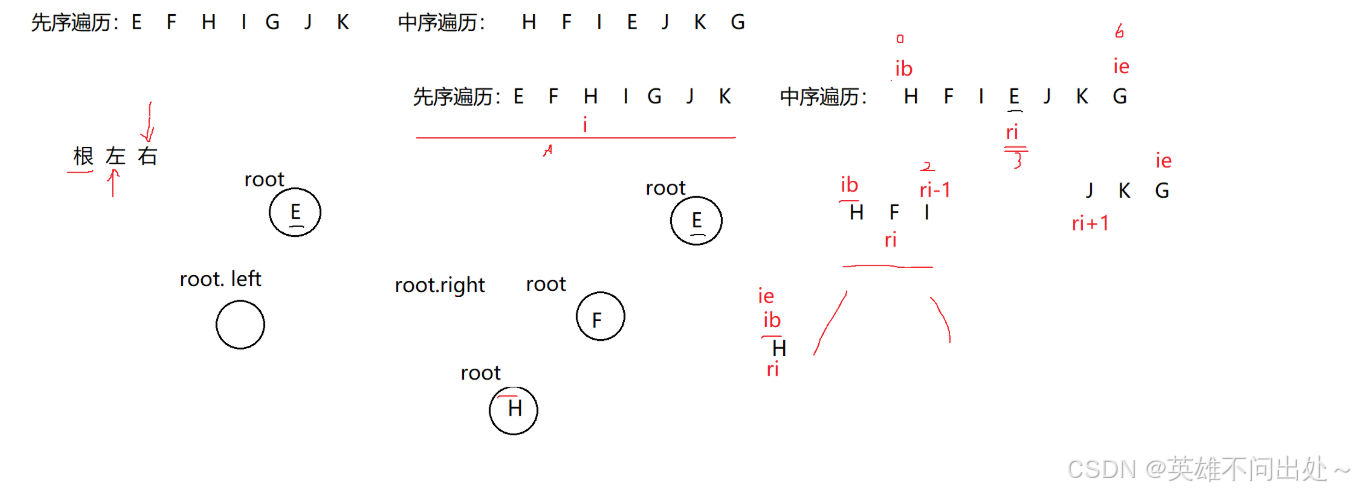
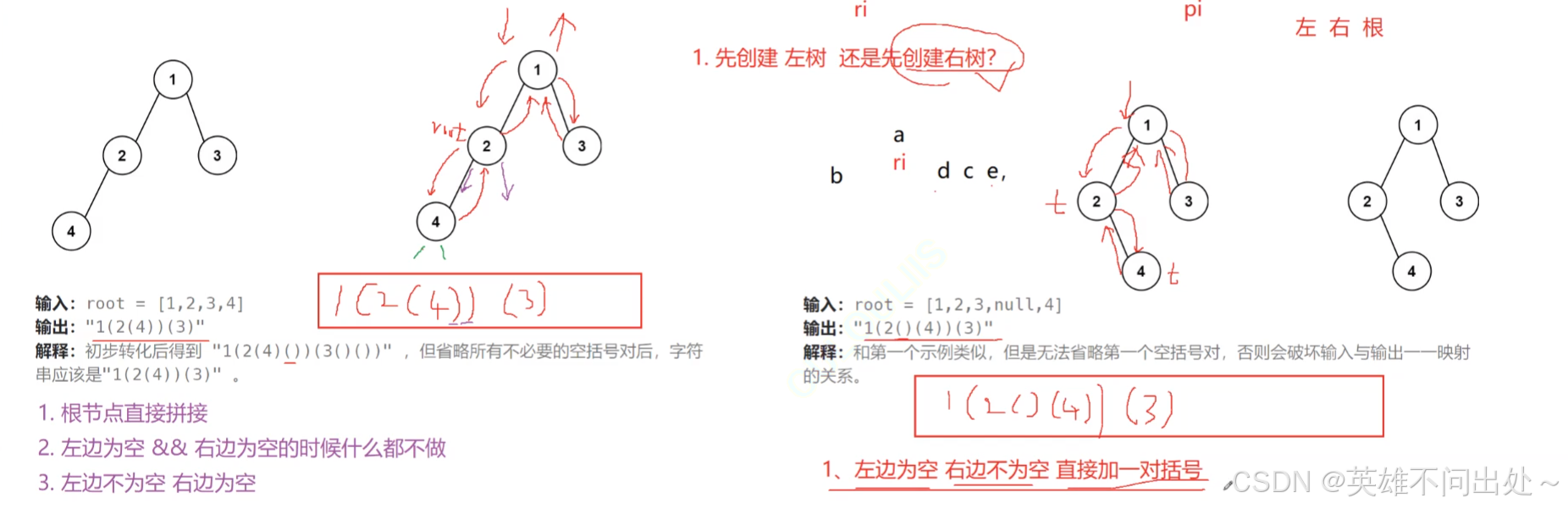
根据前序遍历和中序遍历构建二叉树
根据中序遍历和后序遍历构建二叉树

根据二叉树创建字符串

使用前序遍历的方式进行遍历

层序遍历

1. 可以利用队列从左到右打印节点的值，一个节点进队，在它出队时，可以把它的左节点和右节点分别进队，以此类推

// 层序遍历
    public void levelOrder(TreeNode root){
        if(root == null){
            return ;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while(!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            System.out.print(cur.val + " ");

            if (cur.left != null) {
                queue.offer(cur.left);
            }

            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
    }

判断是不是一颗完全二叉树

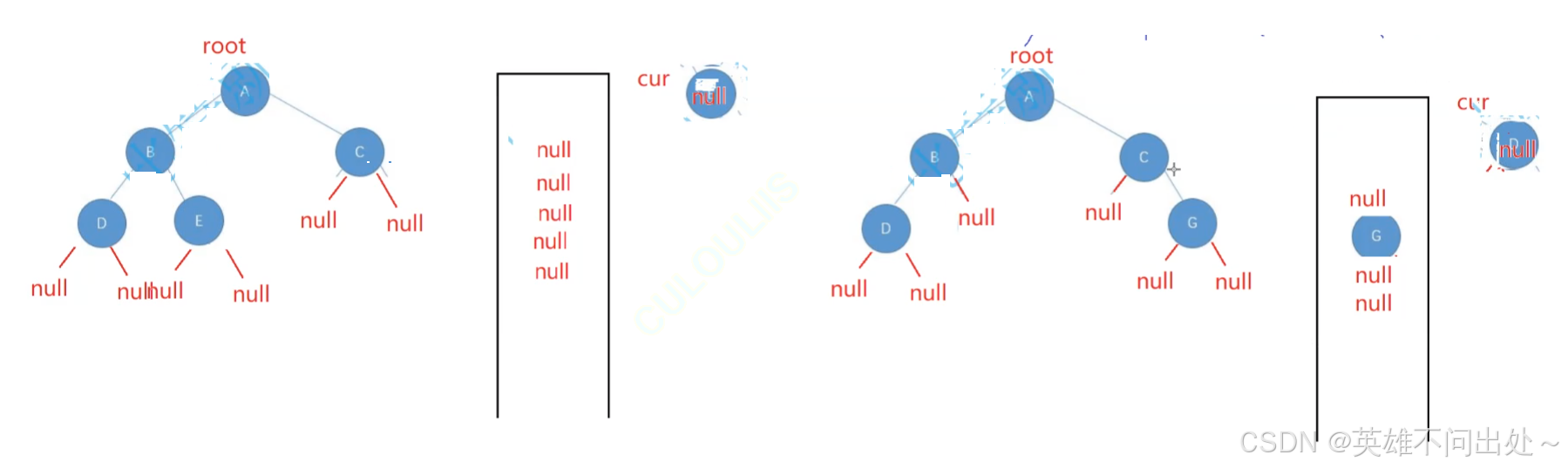
1. 利用队列，如果把所有元素都弹出了，发现队列中都是null，说明是完全二叉树
2. 如果把所有元素都弹出了，发现队列中不完全是null，说明不是完全二叉树

// 判断一棵树是不是一颗完全二叉树
    public boolean isCompleteTree(TreeNode root){
        if(root == null){
            return true;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while(!queue.isEmpty()) {
            TreeNode tmp = queue.poll();

            if(tmp == null){
                break;
            }else{
                queue.offer(tmp.left);
                queue.offer(tmp.right);
            }
        }


        while(!queue.isEmpty()){
            // 一个一个元素出队,判断是否为空
            // 不为空就不是完全二叉树
            TreeNode tmp1 = queue.peek();
            if(tmp1 != null){
                return false;
            }else{
                queue.poll();
            }
        }

        return true;
    }

利用非递归遍历二叉树

前序遍历

1. 利用栈进行存储二叉树的节点，一边存储一边打印二叉树，前序遍历

// 利用栈进行非递归前序遍历
    public void prOrder(TreeNode root){
         if(root == null){
             return;
         }

         Stack<TreeNode> stack = new Stack<>();
         TreeNode cur = root;
         while(cur != null || !stack.isEmpty()){
             while(cur != null){
                 stack.push(cur);
                 System.out.print(cur.val + " ");
                 cur = cur.left;
             }

             TreeNode top = stack.pop();
             cur = top.right;
         }
    }

中序遍历

1. 一直往左走，直到cur为空停止，左树走完了，并且弹出栈顶元素，打印
2. 再遍历弹出元素的右子树

// 利用非递归栈写中序遍历
    public void inOrderNor(TreeNode root){
        if(root == null){
            return;
        }

        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;

        while(cur != null || !stack.isEmpty()) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            // cur为空,弹出元素打印
            TreeNode top = stack.pop();
            System.out.print(top.val + " ");
            cur = top.right;
        }

    }

后序遍历

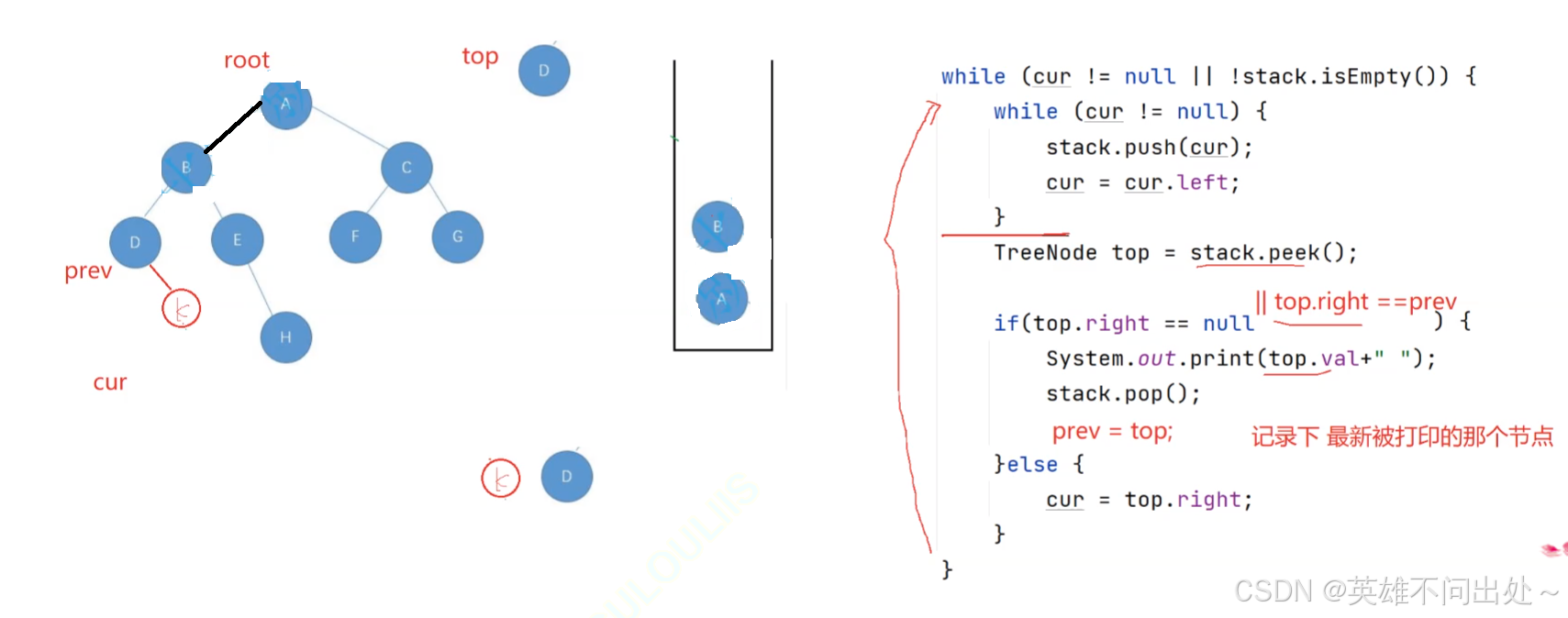
1. 利用prev记录下上次被打印的节点，top的左右都为空或者是上次已经被打印的节点就要打印并且要弹出
2. 画个图自己模拟一遍过程思路会非常清晰
   

// 利用栈实现非递归写后序遍历
    public void postOrderNor(TreeNode root){
        if(root == null){
            return;
        }

        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        TreeNode prev = null;

        while(cur != null || !stack.isEmpty()){
            while(cur != null){
                stack.push(cur);
                cur = cur.left;
            }

            TreeNode top = stack.peek();
            if(top.right == null || top.right == prev){
                System.out.print(top.val + " ");
                stack.pop();
                prev = top;
            }else{
                cur = top.right;
            }
        }
    }