从O(N²)到O(N):我如何给我们的UI框架做了一次"健康大检查"😎
嘿,各位码农伙伴们!我是你们的老朋友,一个在代码世界里快乐"搬砖"的开发者。今天我想和大家聊一个真实发生在我项目里的性能优化故事,它源于一个看似小巧的UI框架,却让我对递归和"剪枝"的艺术有了全新的理解。
我遇到了什么问题?
在我最近参与的一个项目中,我们正在打造一个内部使用的低代码平台。平台的核心功能之一,就是允许业务人员像搭积木一样,通过拖拽组件来构建页面。这些组件在后台被组织成一棵组件树(Component Tree),非常类似于前端框架(如Vue或React)的虚拟DOM树。
一切看起来都很美好,直到我们收到了用户的抱怨:"页面一复杂,预览和操作就变得好卡啊!😭"
经过排查,我们发现问题的根源在于一些"自由奔放"的用户搭建出了非常"奇葩"的组件结构。比如,一个长长的列表,用户不是用一个List组件内嵌多个ListItem,而是用Container组件一个套一个,形成了一条长长的"链条"。
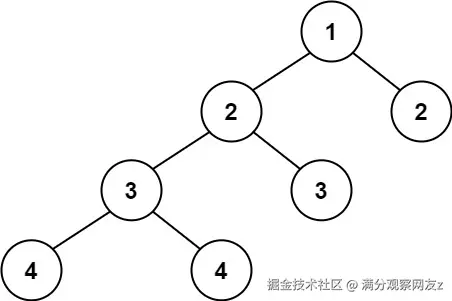
这种极度不平衡 的树,在执行某些需要遍历树深度的操作时(例如:依赖计算、样式应用、布局渲染),性能急剧下降。原本应该是 O(logN) 的深度遍历操作,在"链状树"上退化成了 O(N),而如果对每个节点都执行这类深度计算,总复杂度甚至会飙到 O(N^2)!
为了从根本上解决问题,产品经理提出了一个需求:"我们得给这个平台加一个'健康度'检查功能。如果用户搭建的组件树变得不平衡,就给他一个友好的提示!"
这任务就落到了我的肩上。我需要写一个算法,来判断一棵树是不是"平衡"的。这不就是LeetCode上那道经典的110. 平衡二叉树问题嘛!
我是如何用"后序遍历"解决的
我需要实现一个函数,它能告诉我一棵树是否是平衡的。根据定义,平衡二叉树需要满足:对于树中的任意一个节点,其左、右子树的高度差不能超过1。
我的第一次尝试:直来直去的"暴力解法"
最直观的想法就是,严格按照定义来写代码。
- 写一个函数
height(node),用来计算一个节点的高度。 - 再写一个主函数
isBalanced(node),它做三件事:- 检查当前
node本身的左右子树高度差是不是<=1。 - 递归调用
isBalanced(node.left)检查左子树是否平衡。 - 递归调用
isBalanced(node.right)检查右子树是否平衡。
- 检查当前
代码写出来是这样的:
java
// 这是"自顶向下"的暴力解法,思路清晰但效率低下
private int height(TreeNode node) {
if (node == null) return 0;
return 1 + Math.max(height(node.left), height(node.right));
}
public boolean isBalanced_naive(TreeNode root) {
if (root == null) return true;
boolean rootBalanced = Math.abs(height(root.left) - height(root.right)) <= 1;
return rootBalanced && isBalanced_naive(root.left) && isBalanced_naive(root.right);
}代码提交上去,功能是没问题,但在处理一些层级较深的组件树时,那个"健康度检查"的小按钮转起了圈圈,半天没反应... 😫
我很快就"踩坑"了:这个算法的效率太低了!当我计算父节点的高度时,已经把它的所有子孙节点遍历了一遍;但当我递归下去检查子节点是否平衡时,又会把子节点的子孙们再遍历一遍 !大量的重复计算导致其时间复杂度高达 O(N*logN),在遇到链状树时更是恶化到 O(N^2)。
恍然大悟的瞬间:自底向上的"剪枝"艺术
我坐在椅子上,盯着屏幕沉思🤔... 既然自顶向下的检查存在重复计算,那我能不能换个方向,从下往上检查呢?
当我计算完一个节点的左右子树高度,准备计算它自身的高度时,我不就已经拥有了判断它"是否平衡"所需的所有信息了吗?
💡 "恍然大悟"的瞬间来了! 我可以设计一个函数,它在计算一个节点高度的同时,顺便检查其平衡性。如果发现子树已经不平衡了,就没必要再往上计算了,直接给上面传递一个"不平衡"的信号就行了!这就是剪枝(Pruning)!
我决定改造我的 height 函数,让它承担双重职责:
- 如果子树是平衡的,它就返回该子树的真实高度(一个非负数)。
- 如果子树是不平衡 的,它就返回一个特殊的标记值,比如 -1,来代表"警报"。
这就是经典的后序遍历(左 -> 右 -> 根)思想的应用。我们先深入到最底层,然后层层返回,在返回的途中收集信息并做出判断。
java
/**
* 核心思路:自底向上的后序遍历优化。
* 通过一次遍历,既计算高度又判断平衡性,用-1作为"不平衡"信号实现剪枝。
* 时间复杂度 O(N),每个节点只访问一次。
* 空间复杂度 O(N)(最坏情况)或 O(logN)(平均情况),取决于递归栈的深度。
*/
public boolean isBalanced(TreeNode root) {
// 只需要调用一次辅助函数,根据返回值是否为-1即可判断。
return checkHeight(root) != -1;
}
/**
* 这个辅助函数是整个算法的灵魂!
* 它有两个作用:
* 1. 如果以node为根的子树是平衡的,它返回树的实际高度。
* 2. 如果不平衡,它返回 -1。
*/
private int checkHeight(TreeNode node) {
// 基线条件:空树是平衡的,高度为0。
if (node == null) {
return 0;
}
// 递归处理左子树
int leftHeight = checkHeight(node.left);
// 剪枝!如果左子树已经报告"不平衡",我们就不再浪费时间看右边了,直接把-1这个坏消息传上去。
if (leftHeight == -1) {
return -1;
}
// 递归处理右子树
int rightHeight = checkHeight(node.right);
// 同样,对右子树进行剪枝。
if (rightHeight == -1) {
return -1;
}
// Math.abs() 用来取绝对值,这是判断高度差的核心。
if (Math.abs(leftHeight - rightHeight) > 1) {
// 当前节点不平衡,返回"警报"信号-1。
// 为什么用-1?因为树的正常高度永远是非负数,-1是一个绝佳的、不会混淆的信号值。
return -1;
}
// 如果一切正常,返回当前子树的真实高度。
// Math.max() 帮助我们取左右子树中更高的那一个,再加上当前节点1层。
return 1 + Math.max(leftHeight, rightHeight);
}当我用这个 O(N) 的新算法替换掉旧代码后,"健康度检查"功能瞬间变得丝滑流畅,无论用户搭建出多么"奇葩"的树形结构,都能秒出结果!我露出了满意的微笑。😎
迭代法(使用栈)
为了完全避免递归带来的栈空间开销(虽然本题数据范围不大,但这是一个通用的优化思路),我们可以用一个显式的栈来模拟递归的后序遍历过程。
后序遍历的迭代实现比较复杂。我们需要一个机制来区分一个节点是第一次被访问(应该继续探索其子节点),还是其子节点已经被访问完毕,现在轮到处理它自身了。一个常用的技巧是,在栈中不仅存节点,还存它的状态,或者使用两个栈。
一个更巧妙的单栈方法是:利用 Map<TreeNode, Integer> 来存储已经计算过高度的节点。
- 遍历树,用栈模拟调用栈,一路向左将节点压栈。
- 当无法再往左走,就查看栈顶元素。
- 如果栈顶元素的右子树还没有被访问过(即不在Map中),我们就转向右子树,重复步骤1。
- 如果栈顶元素的右子树已经被访问过或不存在,说明左右子树都处理完了,可以处理栈顶节点了。弹出它,从Map中获取其左右子树的高度,计算平衡性和自身高度,然后存入Map。
这个过程持续到栈为空。
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
/*
* 思路:迭代法。使用一个栈来模拟递归的后序遍历,并用一个哈希表来存储已计算出的子树高度,
* 避免了重复计算,也避免了系统递归栈的开销。
* 时间复杂度:O(N),每个节点入栈、出栈、处理一次。
* 空间复杂度:O(N),栈和哈希表在最坏情况下都需要存储N个节点。
*/
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null)
return true;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode lastVisited = null;
// 使用map来存储已经计算过高度的节及其高度
Map<TreeNode, Integer> map = new HashMap<>();
// 一路向左,将路径上的节点全部压入栈
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
// 查看栈顶节点
cur = stack.peek();
// 如果右子树为空或右子树已经被访问过,则可以处理当前节点
if (cur.right == null || cur.right == lastVisited) {
stack.pop();
// 计算高度和平衡
int leftHeight = map.getOrDefault(cur.left, 0);
int rightHeight = map.getOrDefault(cur.right, 0);
if (Math.abs(leftHeight - rightHeight) > 1)
return false;
map.put(cur, 1 + Math.max(leftHeight, rightHeight));
lastVisited = cur;
cur = null;
} else {
cur = cur.right;
}
}
return true;
}
}解法对比
| 特性 | 解法1 (自顶向下) | 解法2 (自底向上/后序遍历) | 解法3 (迭代法) |
|---|---|---|---|
| 核心思想 | 直接翻译定义,暴力递归 | 后序遍历,一次遍历完成高度计算与平衡检查 | 用栈和哈希表模拟后序遍历 |
| 时间复杂度 | O(N*logN) ~ O(N²) | O(N) | O(N) |
| 空间复杂度 | O(N) | O(N) | O(N) |
| 性能 | 最差,存在大量重复计算。 | 最优,代码简洁且效率高。 | 性能与解法2同级,但常数因子稍大。 |
| 代码复杂度 | 两个递归函数,逻辑清晰但冗余。 | 一个巧妙的递归函数,是本题的标准答案。 | 最复杂,需要手动管理栈和状态,易出错。 |
| 适用场景 | 作为初步思路,易于理解和实现。 | 最佳选择。面试和实际工程中的首选方案。 | 需要避免递归或栈深度有严格限制的场景。 |
举一反三,触类旁通
这种"后序遍历 + 剪枝"的优化思想,在树形问题的处理中简直是"万金油",威力无穷:
- 金融风控系统:在一个交易依赖关系树中,要检查是否存在循环依赖或路径过长导致的风险。我们可以自底向上检查,一旦发现问题环路,就向上层报告异常,中断整个分析。
- 分布式计算:在MapReduce或DAG(有向无环图)任务调度中,一个父任务依赖所有子任务的完成。我们可以用后序遍历的思想,自底向上地确认任务完成状态。一旦有子任务失败,就可以立即"剪枝",将失败状态向上传递,快速失败整个任务链,而不是傻傻地等待其他不相关的分支。
- 自平衡树(AVL树,红黑树):这些高级数据结构在插入和删除节点后,会自底向上地检查平衡因子,并执行旋转操作来恢复平衡。这和我们的"健康检查"思想如出一辙,只不过它们是"边破坏,边治疗"。
这次经历让我深刻体会到,很多时候性能的瓶颈并不在于语言或框架,而在于我们选择的算法。一个看似微小的思路转变------从"自顶向下"到"自底向上"------就能带来天壤之别的性能提升!
更多练手机会
如果你也想对这类树形问题加深理解,强烈推荐下面这几道LeetCode"兄弟"题目,它们的核心思想有异曲同工之妙:
- 相关题目 :
- 543. 二叉树的直径: 和本题非常像,都是通过一次后序遍历同时求解高度和另一个属性(直径)。
- 124. 二叉树中的最大路径和: 后序遍历思想的极致体现,需要在递归返回时做出复杂的决策。
- 104. 二叉树的最大深度: 这是我们"暴力解法"中
height函数的基础版,是掌握树深度计算的敲门砖。
希望我的分享能对你有所启发!下次再遇到树相关的问题时,不妨问问自己:我能用一次遍历解决吗?我能从下往上收集信息吗? 😉