在 《GNSS接收机的定位合集:定位原理,误差来源,定位精度分析》 中,我们介绍了以下内容:
-
• 单机定位的基本原理,为什么需要GNSS接收机定位需要至少4个卫星?
-
• 单机定位中都有哪些影响定位精度的误差源?每个误差源的数量级是多少?
-
• 单机定位精度如何计算。
我们知道,GNSS 接收机的单机定位精度通常只能达到米级,几乎不可能实现亚米甚至厘米级的高精度定位。当我们需要将定位精度提高到厘米级别时,就需要采用差分定位技术。
差分定位系统的组成
差分定位系统由基准站(Base)和移动站(Rover)两部分组成,基本架构如下图所示:
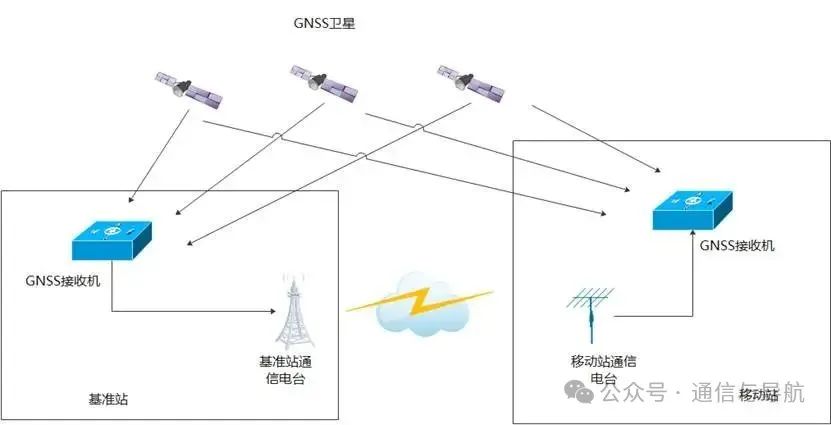
差分系统组成
-
• 基准站和移动站都配备了多频点、多系统的 GNSS 接收机和通信电台。基准站通常是静止的,而移动站可以是静止或运动状态。
-
• 基准站接收来自 GPS、北斗、伽利略、GLONASS 等卫星的信号,采集每个卫星的观测量信息,包括时间、卫星编号、伪距、载波相位、多普勒、信噪比等观测数据,并通过通信电台发送给移动站。
-
• 移动站接收到基准站的观测数据后,结合自身的观测数据,利用差分算法消除公共误差,从而解算出更高精度的位置信息。
这就是差分定位的基本工作流程。
那么:
-
• 差分定位的基本原理是什么,为什么差分定位能够获得高精度?
-
• 为什么说差分定位并不能提到移动站的绝对定位精度?
-
• 差分定位中有哪些误差源?这些误差源还有多少残差?差分定位精度怎么计算?
-
• 载波相位差分和伪距差分的区别?
-
• 为什么双天线能够测向?双天线测向能够达到多少精度?测向精度跟什么相关?
-
• 非差分条件下,单机如何获得高精度位置?
我们将分几个专题来介绍上面这些问题。
单机定位方程
在 《GNSS接收机定位误差分析》 中,我们给出了单机伪距定位的基本方程如下:

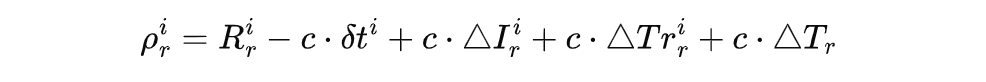
下标 b 表示基准站,r 表示移动站;上标 i 表示第 i 颗卫星。
单差(Single Difference)
当基准站和移动站同时观测同一颗卫星i(共视卫星)时,我们可以把移动站站对卫星i的定位方程,减去,基准站对卫星i的定位方程,形成单差方程:
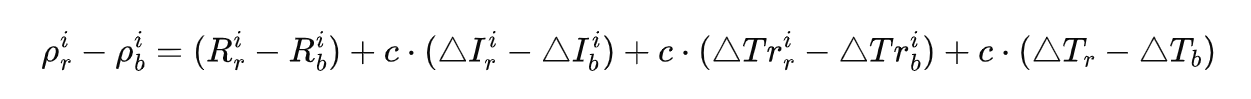
卫星钟差的消除

电离层延时误差的大部分消除

在短基线情况下(移动站和基准站的距离通常小于30km),同一个卫星到基准站和移动站的电离层路径非常相似,电离层延时具有高度的相关性,两个站的电离层延时也高度相似。
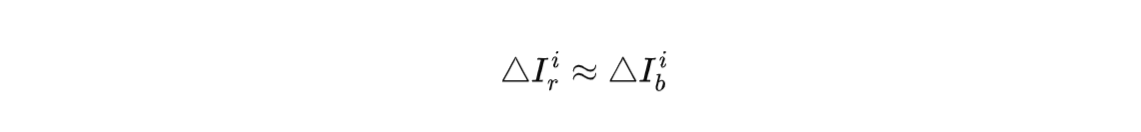
进行单差后,基准站和移动站的电离层延时差可以绝大部分消除。根据NASA CDDIS、IGS站网研究的全球实测统计,30km基线的条件下,电离层延时残余误差不到3cm,已经不影响厘米级的差分定位了。
我们在之前的文章中提到,在GNSS接收机定位中,为了最大限度消除电离层延时误差,最好的方法是同时接收一个卫星的2个频点的信号,比如GNSS接收机同时接收北斗的B1频点和B3频点信号,同时接收GPS的L1频点和L2频点信号,利用双频消除电离层的技术消除电离层延时误差。
但是如果采用差分定位的方式,在短基线的情况下,即使GNSS接收机是单频点的,也能够消除电离层误差的影响,获得高精度的定位结果。
对流层延时误差的大部分消除
在GNSS(北斗、GPS)接收机的定位精度计算提到了对流层延时与大气中的温度、气压、水汽含量、卫星的仰角有关。在用对流层延时模型(北斗和GPS常用的对流层延时模型是Saastamoinen模型)估计的时候,由于水汽含量导致的对流层延时存在比较大的残差。
如果采用单差计算之后呢?
与电离层类似,在短基线情况下,基准站和移动站都处于相似的对流层环境中,因此基准站和移动站的对流层延时也高度相关,两个站的对流层延时也高度相似。
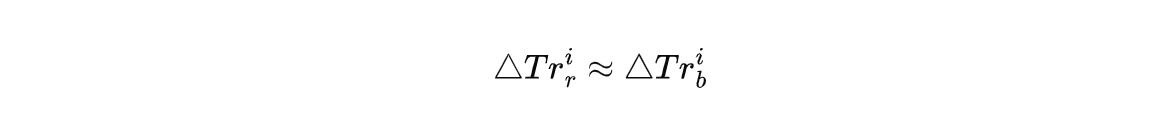
经过单差后,对流层延时差也可以绝大部分消除。
根据RIPE项目 (欧洲永久网)和IGS全球网分析的测试数据,在工程上,在短基线条件下,
-
• 对于中高仰角的卫星(Φ≥30°),单差之后,对流层延时差<1cm,可以忽略;
-
• 对于低仰角卫星(Φ<10°),单差之后,对流层延时差在1cm~5cm。
卫星星历误差的消除
卫星位置误差(星历误差)是指卫星实际轨道与广播星历预报轨道之间的偏差。
当基准站和移动站之间的距离较近,短基线模式下(通常距离小于30km),由于卫星的高度约为20200km,远远大于基准站和移动站之间的距离,因此我们可以认为基准站和移动站对同一个卫星的观测向量是近似平行的。
举例计算:在基准站和移动站之间的基线长度为30km的时候,基准站观测向量和移动站观测向量之间的夹角可以用下面的公式计算:

这个微小角度在工程应用中可以忽略,在差分定位中也可以认为两个观测向量是平行的。如下图:
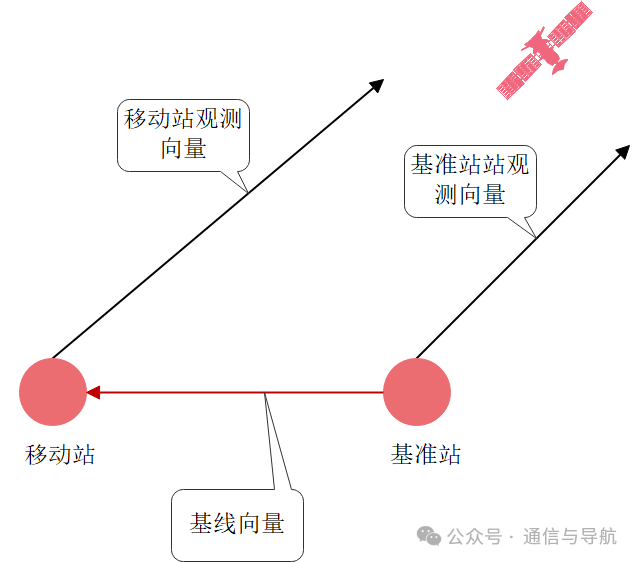
移动站和基准站的观测向量

接收机钟差之差

双差(Double Difference)
基准站和移动站同时接收到i,j两个卫星(i和j两个共视卫星),我们可以分别对卫星 i 和 j 构建单差方程:

我们把卫星i的单差方程减去卫星j的单差方程,可完全消除接收机钟差的影响。
这就是所谓的双差。

总结
单差和双差是 GNSS 差分定位中的核心概念。通过构建单差和双差方程,能够有效消除多个误差源(如卫星钟差、电离层延时、对流层延时和接收机钟差等),显著提高定位精度。在实际应用中,双差方法广泛用于实现厘米级高精度定位,是 RTK(实时动态定位)的基础。
码字不易,大家觉得文章不错,就安排一下一键三连吧:点赞、分享、推荐。