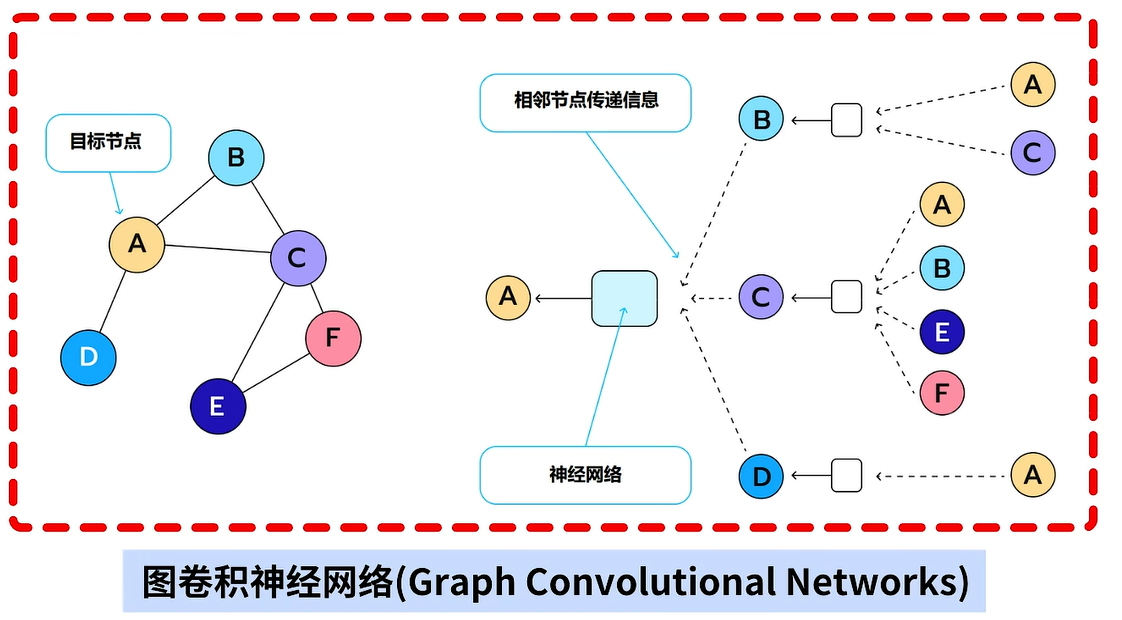
 今天要讲的内容是无卷积神经网络,我们将从三个部分讲解,分别是图数据结构的建立、图卷积和图卷积神经网络。
今天要讲的内容是无卷积神经网络,我们将从三个部分讲解,分别是图数据结构的建立、图卷积和图卷积神经网络。
1.图数据结构的建立
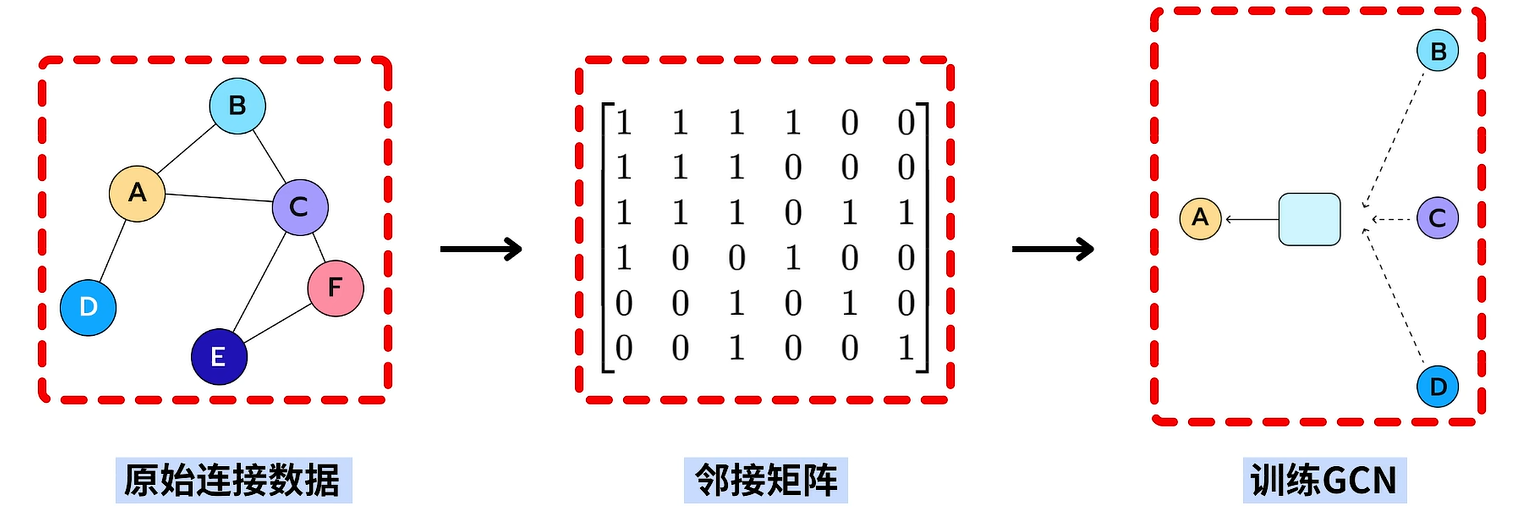
在实验图卷积神经网络前,我们需要先基于图的原始连接数据 ,建立图的数据结构,即邻接矩阵 ,然后再基于邻接矩阵建立并训练图卷积神经网络。

实验中的原始连接数据选用Cora数据集,该数据集是一个被广泛用于图神经网络研究的基准数据集,我们会使用该数据集进行节点分类任务的实验。在左侧图中,节点的不同颜色就表示了不同的类别。
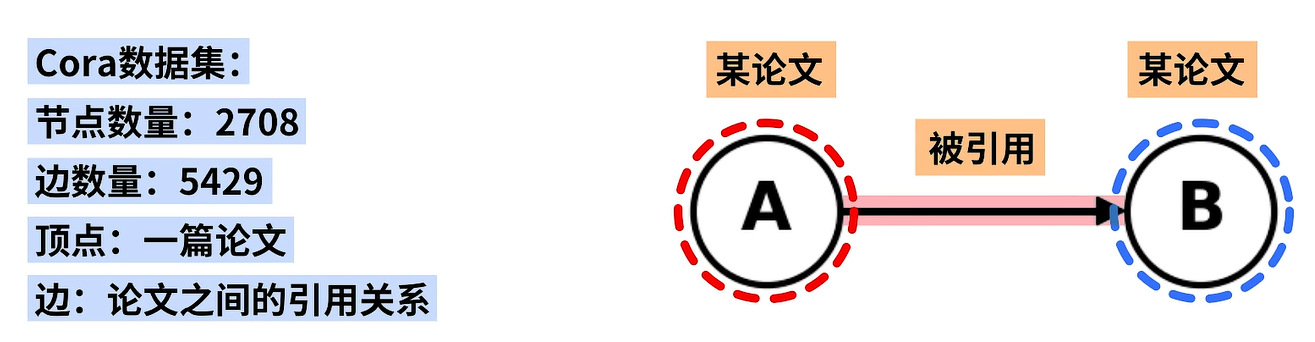
Cora数据集中包含了2708个节点和5429条边,每个节点代表一篇论文,每条边代表论文之间的引用关系。例如,如果结点a指向另一个结点b,就说明结点b代表的论文引用了结点a代表的论文,即a被b引用。
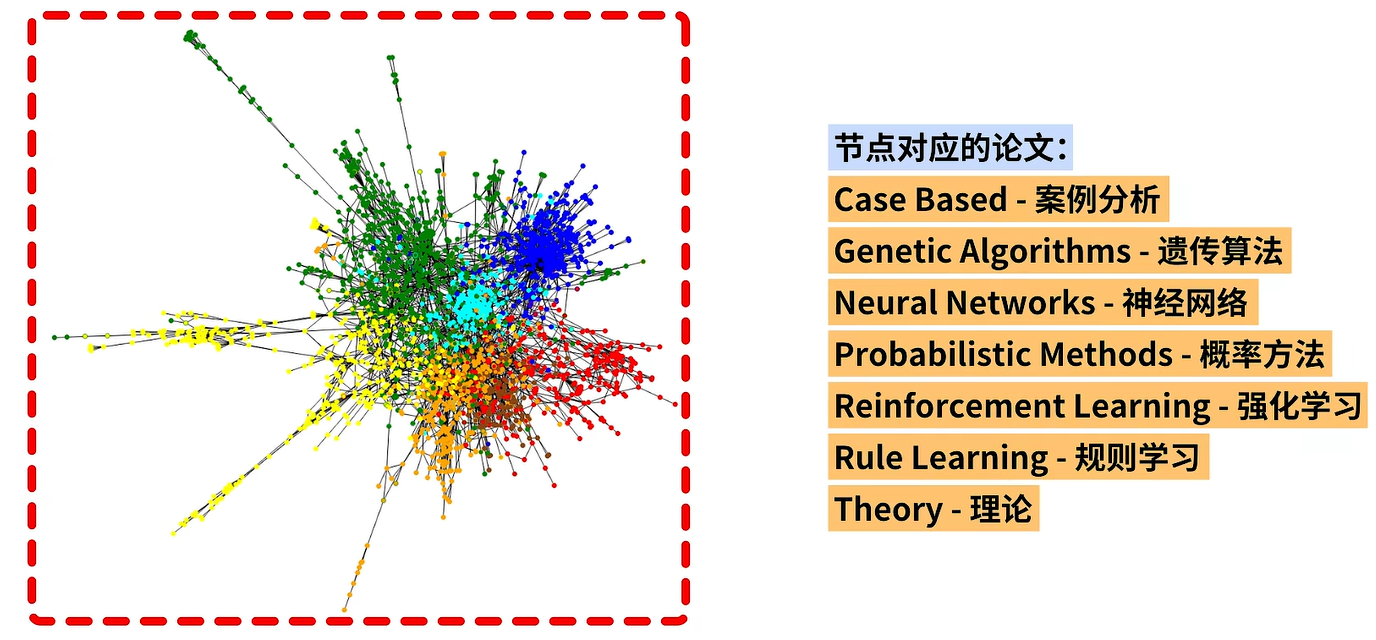
Coral数据集中的节点对应的论文被分为了案例推理、遗传算法、神经网络等七个类别。我们的目标就是:将图中的结点打上这七个标签中的一个,每个节点都有一个特征向量用于描述该节点对应论文的特征属性。
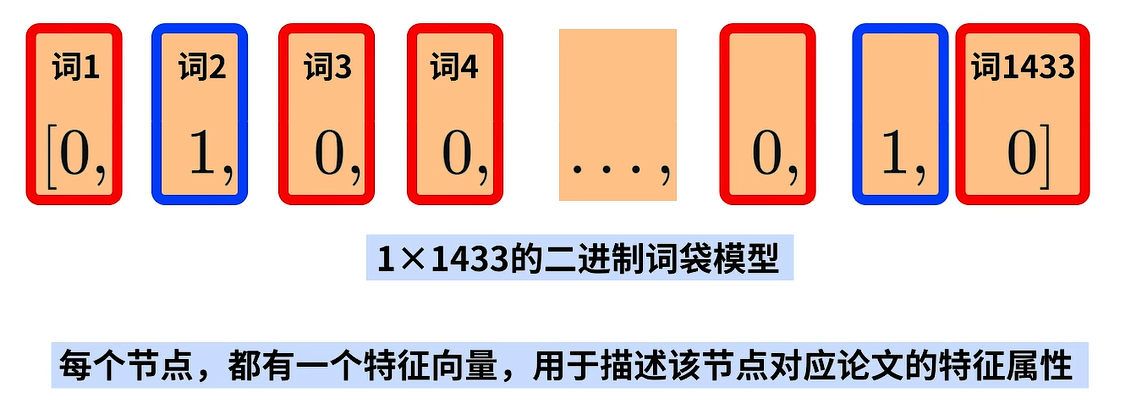
这个特征向量是一个143维的二进制向量模型,每一维都对应了一个关键词,其中1表示该词出现在论文中,0表示没有出现。
具体来说,在Coral数据集中,有两个文件,分别是Cora.cities和Cora.content。
打开文件Cora.cities,其中保存了结点之间的引用关系,每行有两列对应两个论文id。第一列表示被引用论文的id,第二列表示引用论文的论文id。例如,第一行的35,1033就表示了1033号论文引用了35号论文,从35号论文有一条边指向1033号论文。

文件Coral.content,保存了节点id、节点特征向量和节点标签。第一列表示结点id,随后是二进制的特征向量,一共有143列表示143个特征,最后一列是结点的类别标签。

下面我们要基于这两份数据建立图的数据结构,也就是输入Cora.cities和Cora.content,输出图的连接矩阵。
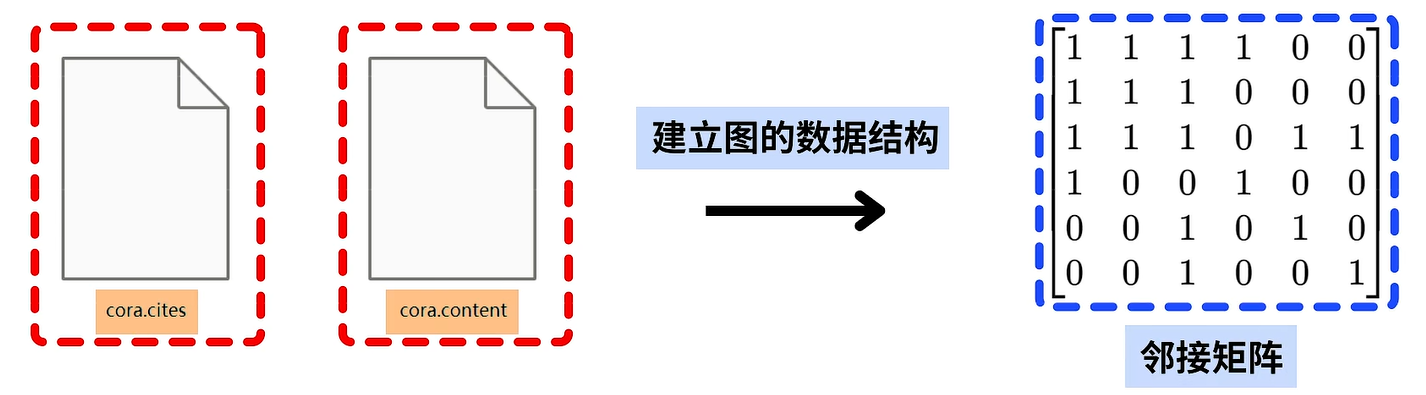
一共两个文件:cora.cires:边的信息。cora.content:节点的特征。
- 链接:https://pan.baidu.com/s/1bVAi4uhKGQU0sbTRljbg-Q
- 提取码:1111
代码如下,
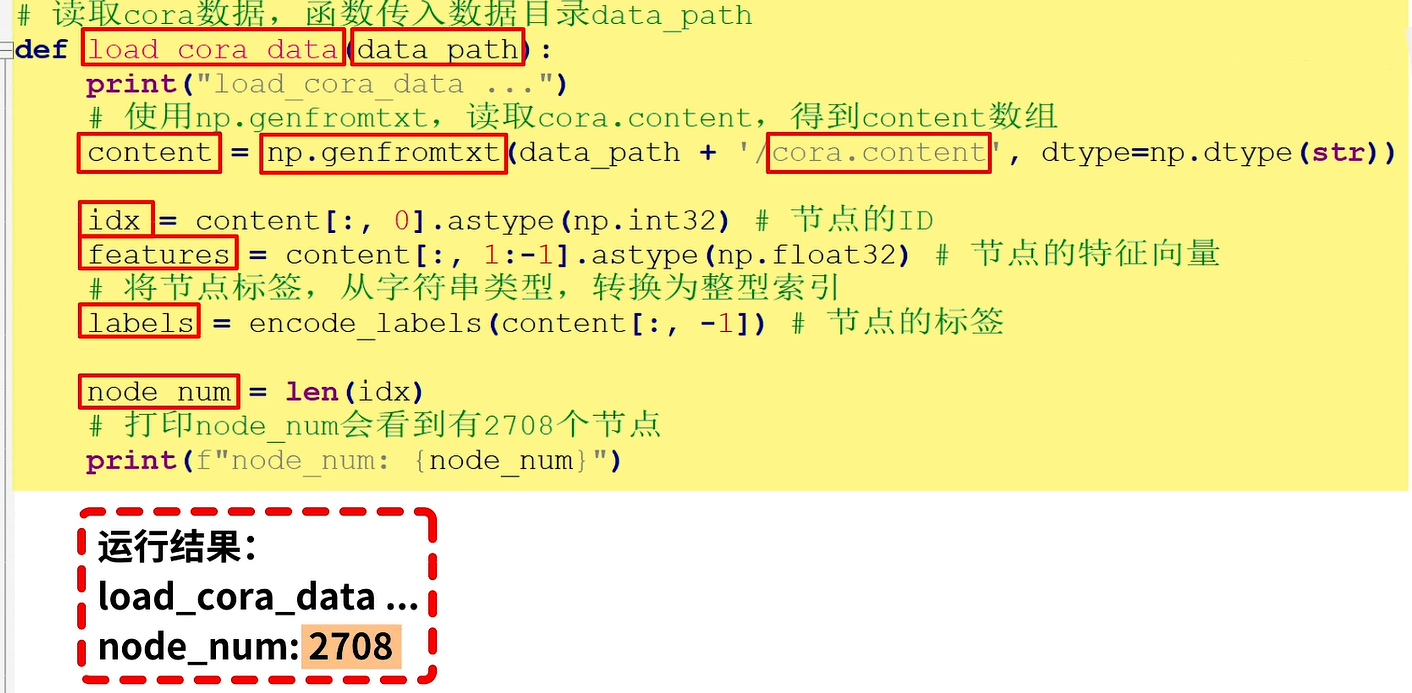
第一,实现load_coral_data函数读取Cora数据,函数传入数据目录。在函数中首先使用np.genfromtxt读取Cora.content得到content的数组,然后将content数组拆分为结点的id、结点的特征向量、结点的标签。使用node_num保存结点的数量,打印后会有2708个节点。这里需要使用encode_labels将结点标签labels从字符串类型转换为整形索引。
这里需要使用encode_lables()函数:将节点标签从字符串类型,转换成整型索引。例如,七种类别标签会被转换为0到6共7个数字。

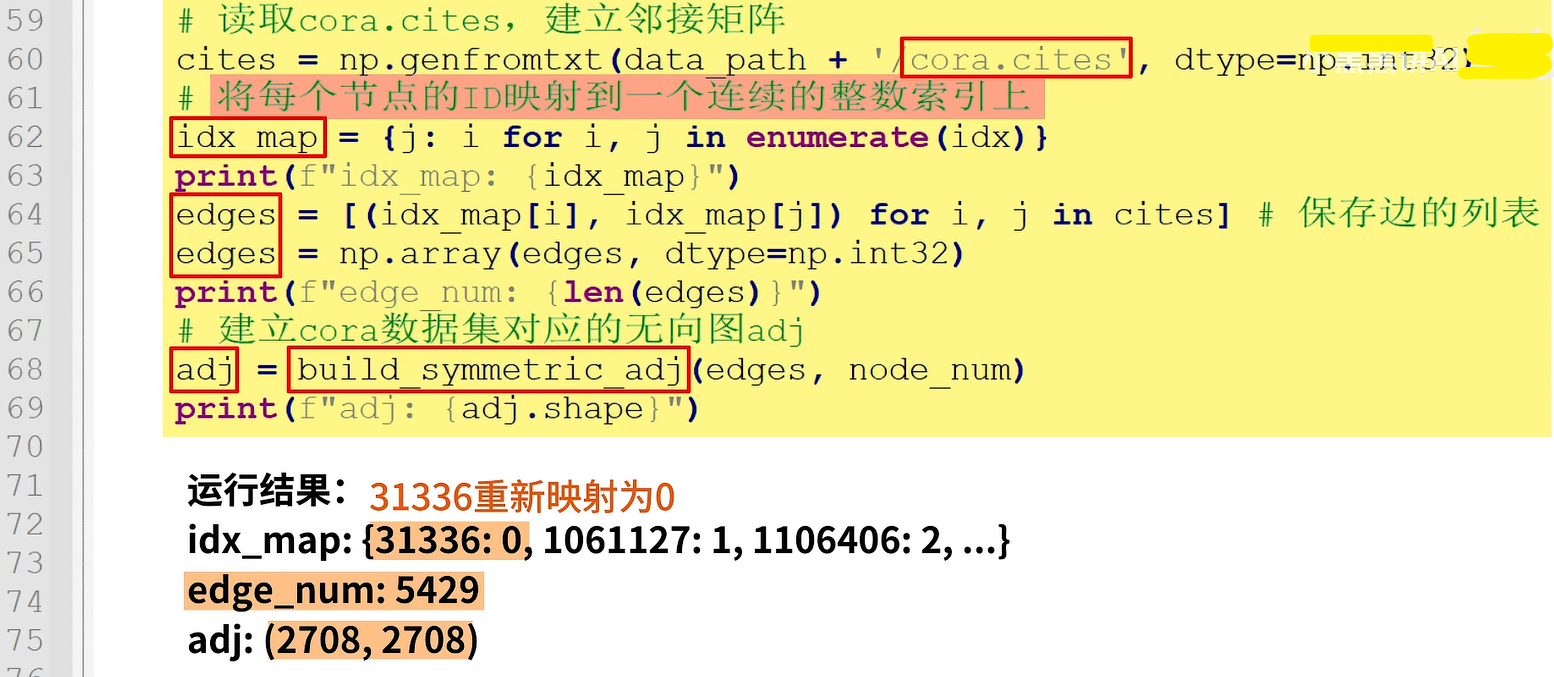
第二,读取Cora.cities文件,建立邻接矩阵。
首先,创建idx_map,将每个结点的id映射到一个连续的整数索引上。例如,31336:0表示31336重新映射为零。
然后定义保存边的列表edges,打印edge_num会看到是5429。
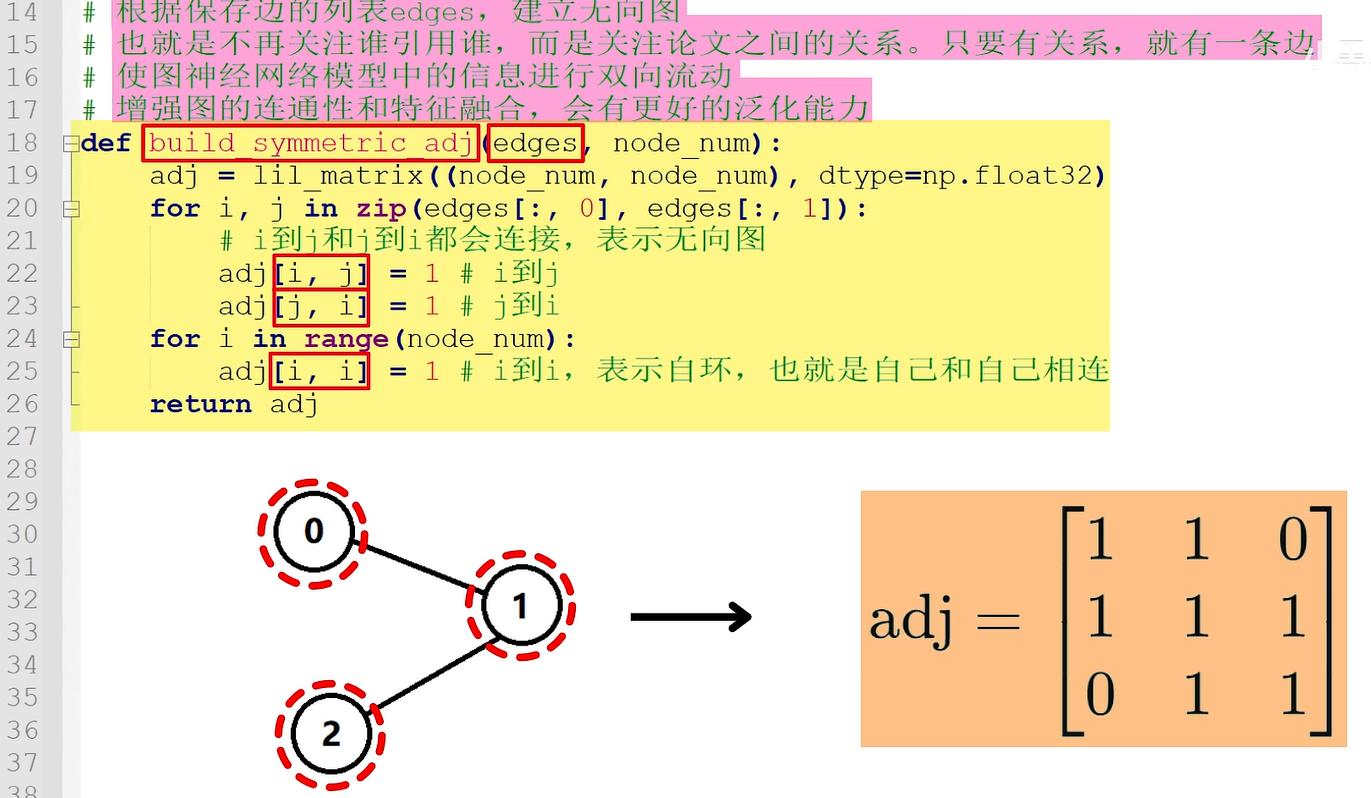
然后调用build_symmetric_adj()函数建立cora数据集对应的无向图adj,打印adj的尺寸是2708x2708。
函数build_symmetric_adj()根据保存边的列表edges建立无向图,即不再关注谁引用谁,而是关注节点之间的关系。只要有关系就有一条边,这样做的好处是使图神经网络中的信息进行双向流动,增强图的连通性和特征融合,会有更好的泛化能力。其中i到j和j到i都会进行连接,从而表示无向图。另外i到i表示自环,即自己和自己相连。例如,包括0、1、2一共3个结点的图会被转换为三乘三的邻接矩阵。
第三,调用normalize函数对features和adj进行标准化处理,再将features、labels和adj转换为张量返回。
2.图卷积
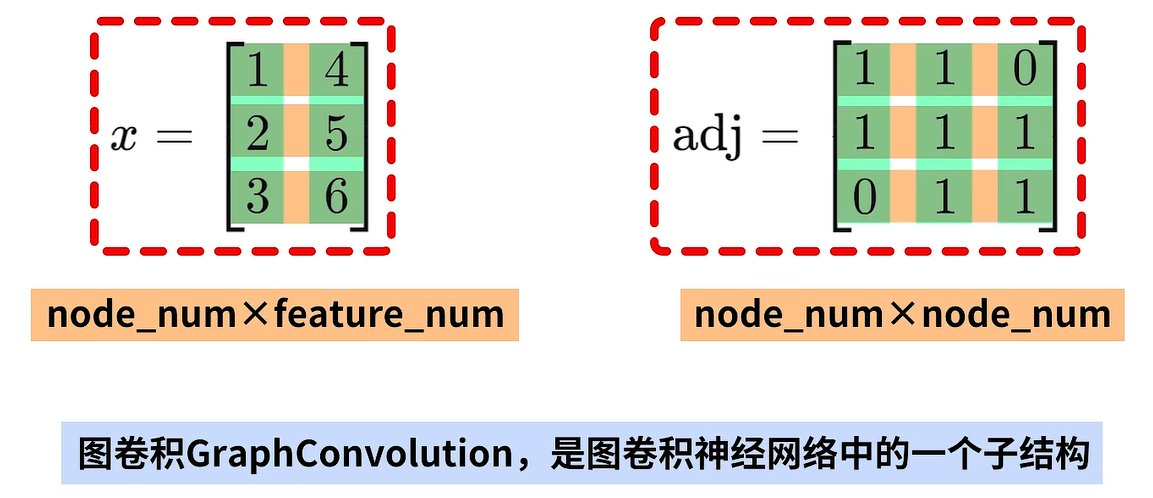
图卷积GraphConvolution是图卷积神经网络中的一个子结构,图卷积的输入数据是特征向量x和图的邻接矩阵adj。其中x是结点数node_num乘特征数feature_num大小的矩阵,adj是节点数node_nume乘node_num大小的方阵。例如,这里展示了三个结点的图,每个结点有两维特征,所以x是三乘二的矩阵,adj是三乘三的方阵。
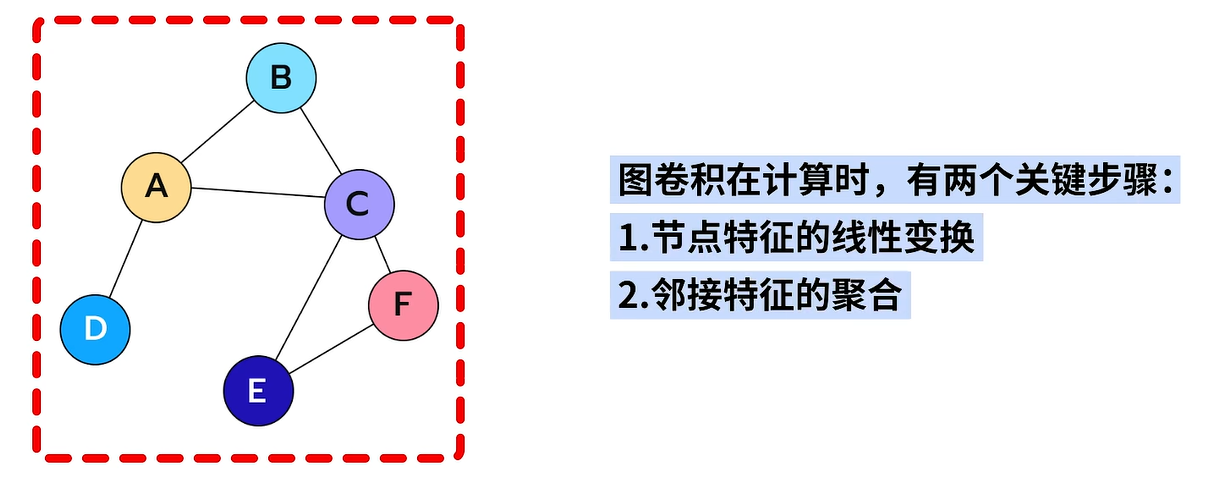
图卷积在计算时有两个关键步骤,分别是1.结点特征的线性变换 和2.结点邻接特征的聚合。
具体来说,在图卷积中包含了一个线性层,我们会使用该线性层对结点特征x进行线性变换,即进行特征提取,图卷积中的可训练参数都在线性层中。
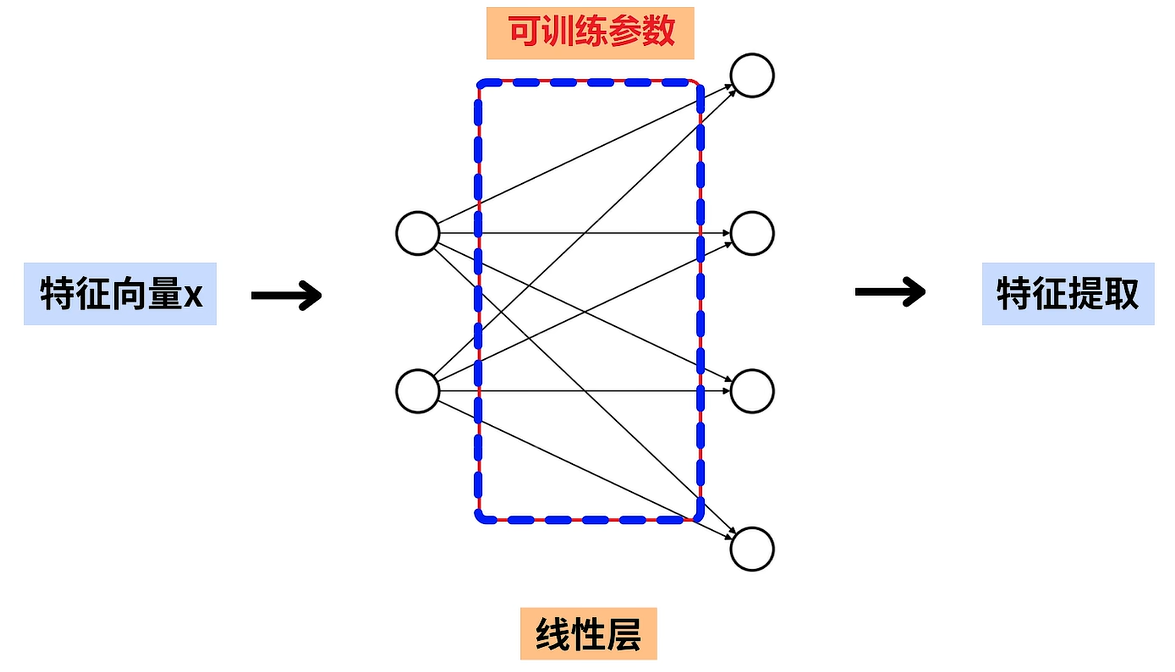
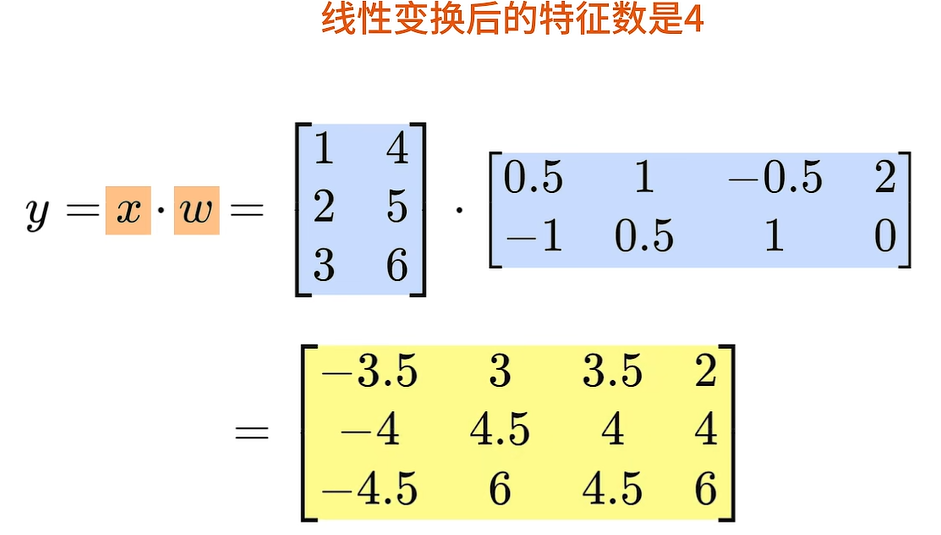
例如,X是一个三乘二的矩阵,如果线性变化后的特征数是四,那么就会使用3x2的矩阵X 乘以二2x4大小的权重矩阵W得到3x4大小的输出结果。
第二个关键步骤是:使用邻接矩阵adj进行结点的特征聚合,具体会将邻接矩阵adj和特征向量X进行矩阵相乘,这个步骤会通过图传导每个节点中的特征信息。
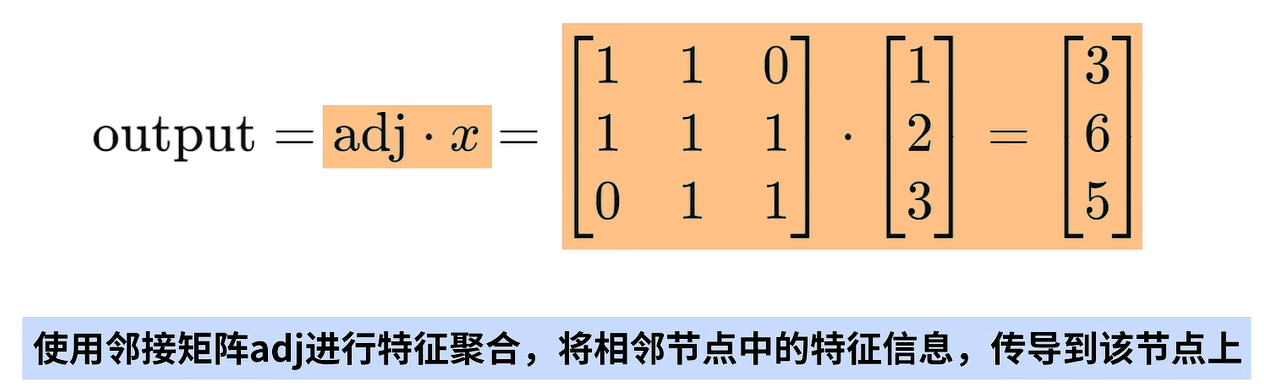
例如,特征向量x是3x1大小的,代表了三个结点,每个节点有一个特征,特征值分别是1、2、3。邻接矩阵adj是3x3大小的,对应了三个结点的无向图。
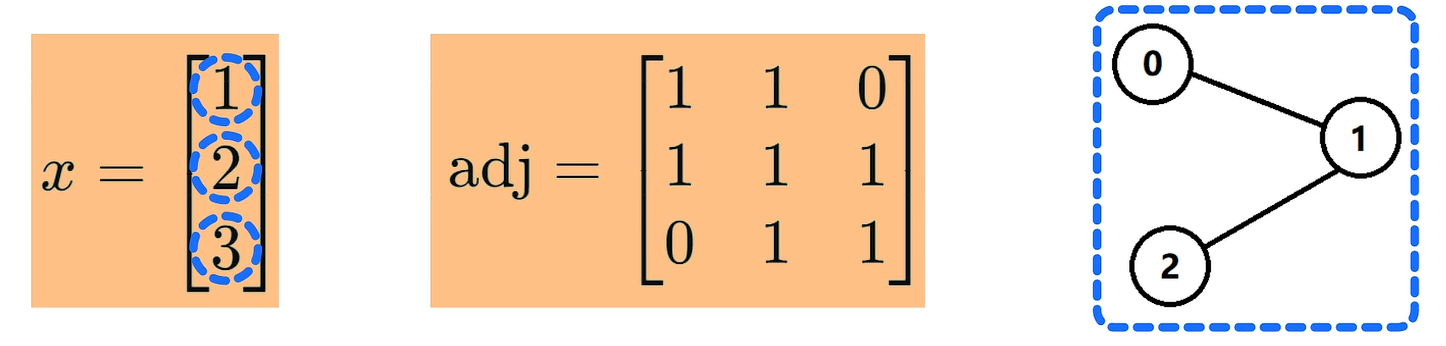
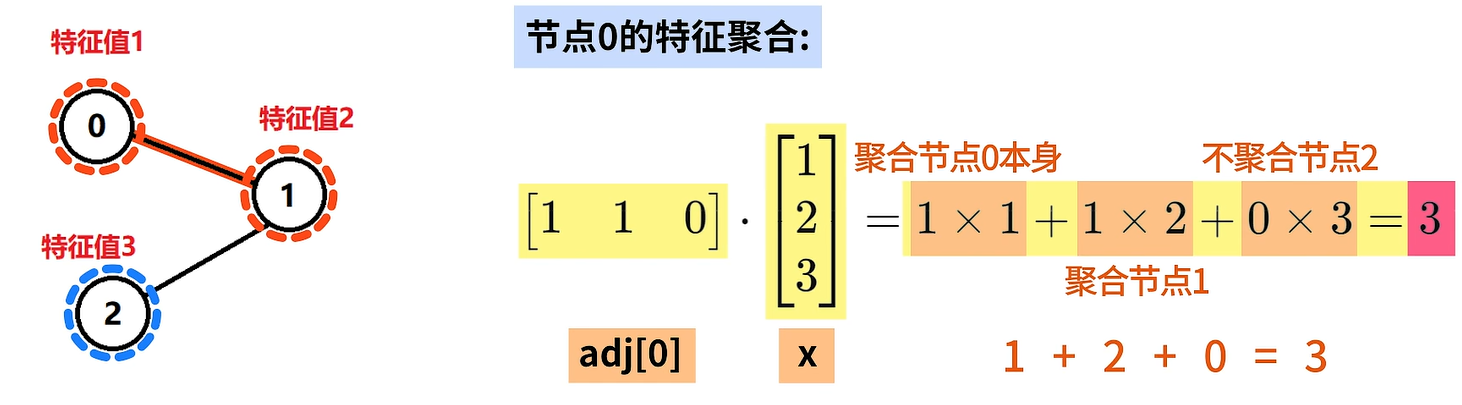
我们先来关注节点0的特征聚合,节点0与节点0本身节、点1相连和结点2不相连,所以adj的第零行是1、1、0,将它和x相乘就会得到结点0的相邻特征,聚合结果为3。这里的1x1表示聚合结点0本身的特征值1,1x2表示聚合结点1的特征值,0x3表示不聚合结点2的特征值,因此最后的结果等于3。
同理,接着计算结点1和节点2的特征聚合,得到结果如下:
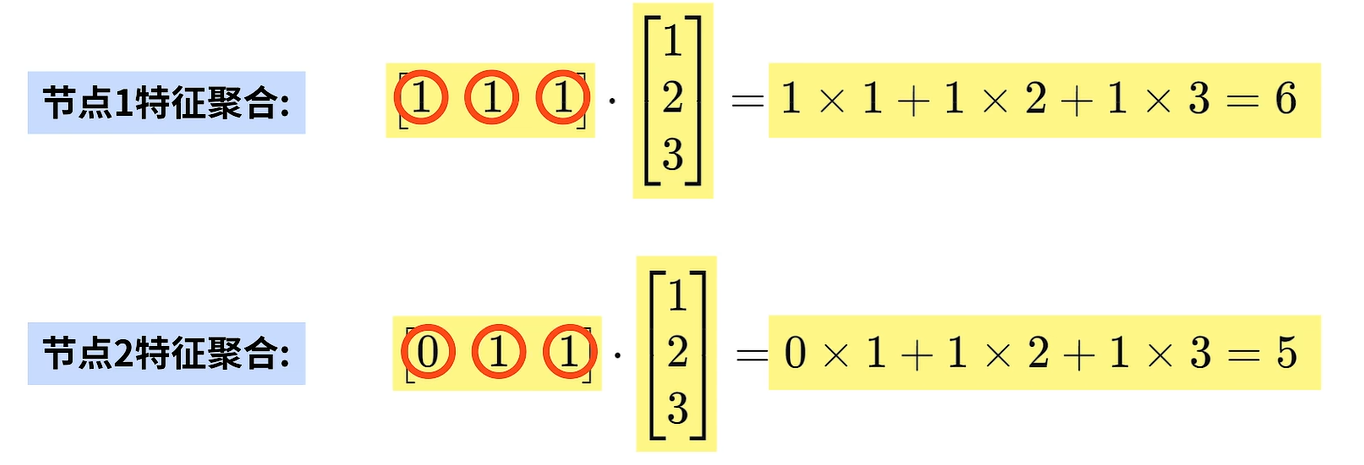
图卷积的Pytorch代码实现如下
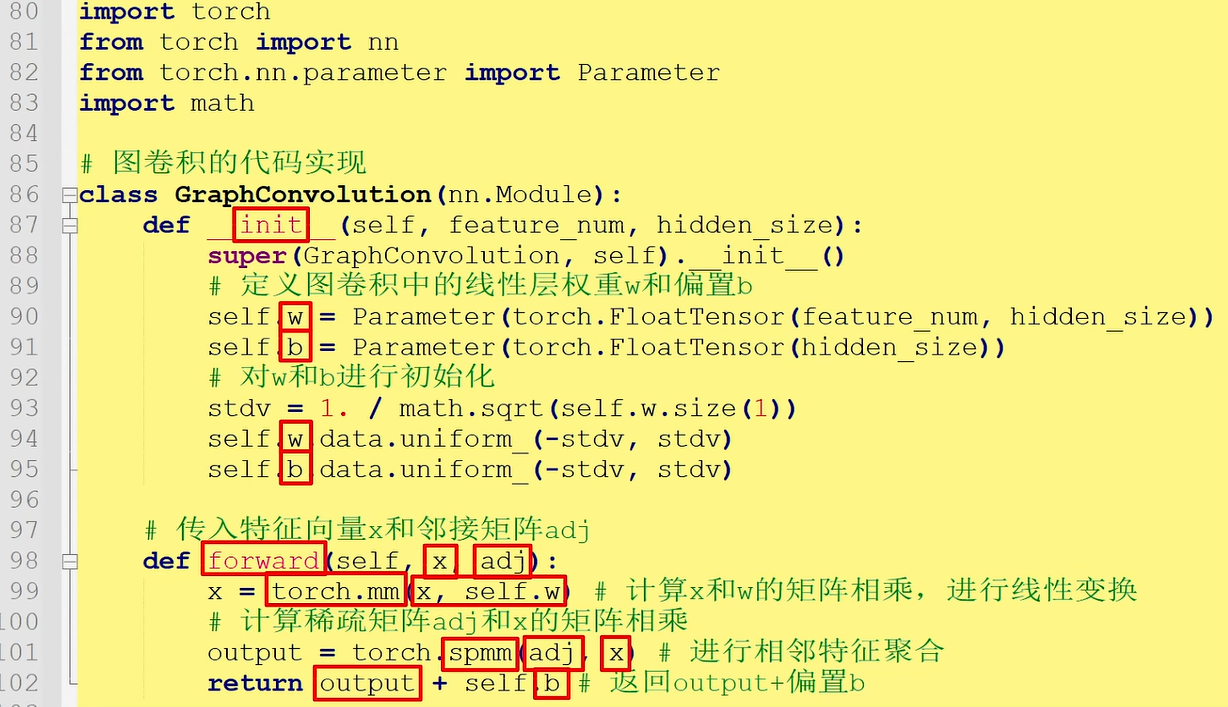
在init函数中定义图卷积中的线性层权重w和偏置b,并对w和b进行初始化;
在forward函数中传入特征向量x和邻接矩阵adj,使用torch.mm计算x和w的矩阵相乘,进行线性变换;使用torch.spmm计算稀疏矩阵adj和x的矩阵相乘,进行相邻特征聚合;最后函数返回output加偏置b。
3.图卷积神经网络
实现完图卷积后就可以构建图卷积神经网络了。

在GCN的init函数中,定义图卷积层gc1,relu激活函数,dropout层,图卷积gc2;
在forward函数中,传入特征向量x和邻接矩阵adj,按照gc1 relu、dropout和gc2的顺序计算前向传播。
最后实现图卷积神经网络的训练和测试。
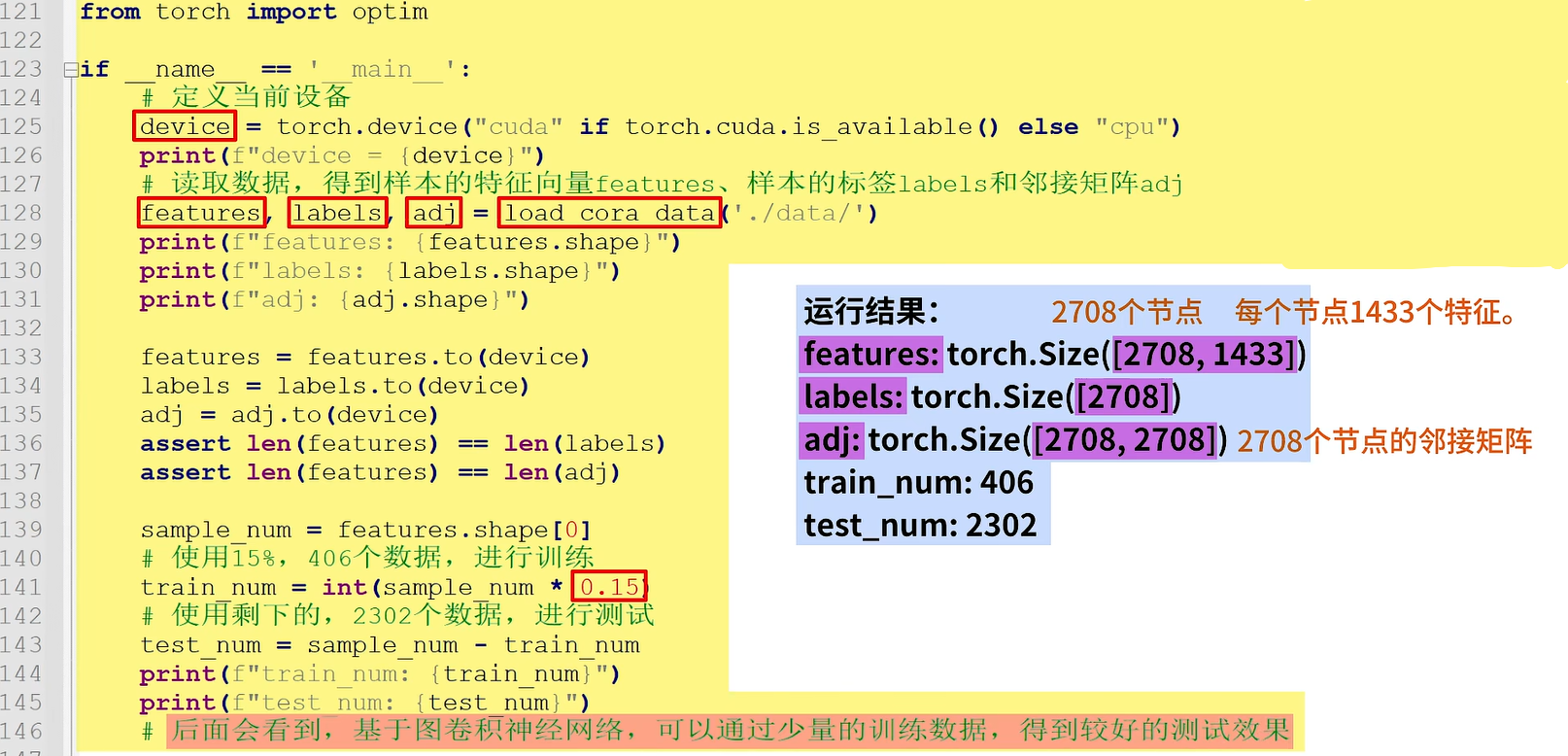
首先,定义当前设备device,
接着,使用load_coral_data读取数据,得到样本的特征向量features、样本的标签labels和邻接矩阵adj。这里features的大小是2708x1433,表示2708个节点,每个节点有1433个特征;labels的大小是2708;adj的大小是2708x2708,表示2708个结点的邻接矩阵。
使用15%的数据,即406个数据进行训练,使用剩下的数据进行测试。后面会看到基于图卷积神经网络可以通过少量的训练数据得到较好的测试效果。

接着获取输入特征数feature_num,定义隐藏特征数为16,样本标签数class_num,设置dropout率为0.5,创建GCN模型model,将模型调整为训练模式,定义优化器optimizer和交叉熵损失函数criterion。
接着进入3000轮的循环迭代。
首先将梯度清零,进行前向传播。这里要说明的是,图卷积神经网络的前向传播有些特殊。在图卷积神经网络的前向传播阶段,需要计算图中所有结点的特征表示,即将features和adj全部传入到model,计算出output。这是因为每个节点的特征更新不仅依赖于其自身的特征,还依赖于其邻居结点的特征。即那些不在训练集中的结点的特征,会影响到训练集中的结点的特征表示。我们要将图中的节点和它的特征看作是一个整体来理解和处理,这是分析和处理图数据结构的基本原则。
接着进行损失计算。在计算损失时只计算训练集结点的损失,即只使用train_name的样本计算损失,最后使用backward计算梯度,使用optimizer.step计算梯度下降。

完成训练后将模型调整为测试模式,基于全量特征计算outputs,然后将测试样本的预测结果保存到predict。最后。计算正确率accuracy。运行程序,可以看到,经过3000轮的迭代测试,测试集正确率是81.4%。
4.完整代码(jupyter格式)
python
import math
import time
import torch
import torch.nn as nn
import numpy as np
import scipy.sparse as sp
from torch import optim
from scipy.sparse import lil_matrix
from sklearn.preprocessing import normalize
from torch.nn.modules.module import Module
from torch.nn.parameter import Parameter
#读取cora数据,函数传入数据目录data_path
def load_cora_data(data_path):
print("load_cora_data...")
#使用np.genfromtxt,读取cora.content,得到content数组
content = np.genfromtxt(data_path + '/cora.content', dtype=np.dtype(str))
idx = content[:,0].astype(np.int32)# 节点的ID
features =content[:,1:-1].astype(np.float32)#节点的特征向量
#将节点标签,从字符串类型,转换为整型索引
labels = encode_labels(content[:,-1])#节点的标签
node_num = len(idx)
#打印nodenum会看到有2708个节点
print(f"node_num: {node_num}")
#打印labels
print(labels)
#读取cora.cites,建立邻接矩阵
cites_= np.genfromtxt(data_path + "/cora.cites", dtype=np.int32)
#将每个节点的ID映射到一个连续的整数索引上
idx_map = {j: i for i, j in enumerate(idx)}
print(f"idx_map: {idx_map}")
edges = [(idx_map[i], idx_map[j]) for i, j in cites_] #保存边的列表
edges = np.array(edges, dtype=np.int32)
print(f"edge_num: {len(edges)}")
#建立cora数据集对应的无向图adj
adj = build_symmetric_adj(edges, node_num)
print(f"adj: {adj.shape}")
features = normalize(features) #标准化处理
adj = normalize(adj) #标准化处理
features = torch.FloatTensor(features) #转换为张量
labels = torch.LongTensor(labels) #转换为张量
adj = adj_to_sparse_tensor(adj) #转换为张量
return features, labels, adj
load_cora_data("D:\python_project\gcn_project\data")
#将节点标签,从字符串类型,转换为整型索引
def encode_labels(labels):
classes = sorted(set(labels))
label2index = {label: idx for idx, label in enumerate(classes)}
indices = [label2index[label] for label in labels]
indices = np.array(indices, dtype=np.int32)
return indices
encode_labels(['Neural_Networks', 'Genetic_Algorithms', 'Reinforcement_Learning', 'Neural_Networks'])
#根据保存边的列表edges,建立无向图
#也就是不再关注谁引用谁,而是关注论文之间的关系。只要有关系,就有一条边
#使图神经网络模型中的信息进行双向流动
#增强图的连通性和特征融合,会有更好的泛化能力
def build_symmetric_adj(edges, node_num) :
adj = lil_matrix((node_num, node_num), dtype=np.float32)
for i, j in zip(edges[:, 0], edges[:, 1]):
#i到j和j到i都会连接,表示无向图
adj[i,j] = 1 # i到j
adj[j, i] = 1 # j到i
for i in range(node_num) :
adj[i,i]=1 #i到i,表示自环,也就是自己和自己相连
return adj
def adj_to_sparse_tensor(adj):
"""将scipy稀疏矩阵转为torch稀疏张量"""
adj = adj.tocoo()
indices = torch.from_numpy(
np.vstack((adj.row, adj.col)).astype(np.int64)
)
values = torch.from_numpy(adj.data)
shape = torch.Size(adj.shape)
return torch.sparse.FloatTensor(indices, values, shape)
#图卷积的代码实现
class GraphConvolution(nn.Module):
def __init__(self, feature_num, hidden_size):
super(GraphConvolution, self).__init__()
#定义图卷积中的线性层权重w和偏置b
self.w = Parameter(torch.FloatTensor(feature_num, hidden_size))
self.b = Parameter(torch.FloatTensor(hidden_size))
#对w和b进行初始化
stdv = 1. / math.sqrt(self.w.size(1))
self.w.data.uniform_(-stdv, stdv)
self.b.data.uniform_(-stdv, stdv)
#传入特征向量x和邻接矩阵adj
def forward(self, x, adj):
#计算x和w的矩阵相乘,进行线性变换
x = torch.mm(x, self.w)
#计算稀疏矩阵adj和x的矩阵相乘
output = torch.spmm(adj, x)
#进行相邻特征聚合
return output + self.b # 返回output+偏置b
#实现图卷积神经网络 class GCN(nn.Module) :
class GCN(nn.Module):
def __init__(self, input_size, hidden_size, output_size, dropout):
super(GCN, self).__init__()
self.gc1 = GraphConvolution(input_size, hidden_size) # 图卷积
self.relu = nn.ReLU() #激活函数
self.drop = nn.Dropout(dropout) # dropout层
self.gc2 = GraphConvolution(hidden_size, output_size)# 图卷积
#传入特征向量x和邻接矩阵adj,计算前向传播
def forward(self, x, adj):
X = self.gc1(x, adj)
X = self.relu(X)
X = self.drop(X)
X = self.gc2(X, adj)
return X
if __name__ == "__main__":
#定义当前设备
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"device = {device}")
# 读取数据,得到样本的特征向量features、样本的标签labels和邻接矩阵adj
features, labels, adj = load_cora_data('./data/')
print(f"features: {features.shape}")
print(f"labels: {labels.shape}")
print(f"adj: {adj.shape}")
features = features.to(device)
labels = labels.to(device)
adj = adj.to(device)
assert len(features) == len(labels)
assert len(features) == len(adj)
sample_num = features.shape[0] #使用15%,406个数据,进行训练
train_num = int(sample_num * 0.15) #使用剩下的,2302个数据,进行测试
test_num = sample_num - train_num
print(f"train_num: {train_num}")
print(f"test_num: {test_num}")
# 后面会看到,基于图卷积神经网络,可以通过少量的训练数据,得到较好的测试效果
feature_num = features.shape[1] #输入特征数
hidden_size = 16 #隐藏层特征数
class_num = labels.max().item() + 1 #样本标签数量
dropout = 0.5 # dropout率
print(f"feature_num: {feature_num}")
print(f"hidden_size: {hidden_size}")
print(f"class_num: {class_num}")
#创建GCN模型
model = GCN(feature_num, hidden_size, class_num, dropout).to(device)
model.train() #调整为训练模式
optimizer = optim.Adam(model.parameters()) # Adam优化器
criterion = nn.CrossEntropyLoss() #交叉熵损失函数
n_epoch = 3000
for epoch in range(1, n_epoch + 1): # 3000轮的迭代循环
optimizer.zero_grad() # 将梯度清零
#图卷积神经网络的前向传播有些特殊
#在图卷积网络的前向传播阶段,需要计算图中所有节点的特征表示井
#将features和adj,全部传入到model,计算出output
outputs = model(features, adj)
#每个节点的特征更新,不仅依赖于其自身的特征,还依赖于其邻居节点的特征也就是,那些不在训练集中的节点的特征,会影响到训练集中节点的特征表示
#我们要将图中的节点和它的特征,看做是一个整体来理解和处理
#这是分析和处理图数据的基本原则
#计算损失:
#在计算损失时,只计算训练集节点的损失
loss = criterion(outputs[:train_num], labels[:train_num])
loss.backward() # 计算梯度
optimizer.step() # 梯度下降
if epoch % 100 == 0:
print(f'Epoch {epoch}/{n_epoch}, Loss: {loss.item():.3f}')
#测试模型
model.eval() # 将模型调整为测试模式
outputs= model(features, adj)#基于全量特征计算结果
predicted = torch.argmax(outputs[train_num:], dim=1)#测试样本的预测结果
correct = (predicted == labels[train_num:]).sum().item()
accuracy= 100 * correct / test_num #计算正确率
print(f'Accuracy: {correct}/{test_num}={accuracy:.1f}%')