今天打算开始 3D 数学基础的复习,本文假设你了解以下概念:一次多项式、矩阵、向量 ,基于以上拓展的概念 归一化、2~3阶矩阵的几何意义。
几何意义结论
- 齐次坐标是对三维的人工的特定的 升维,它是一个工具 而已。图形学中常用来作为变换矩阵(平移、斜切、旋转、缩放)中的平移 。因为平移 是一个仿射变换(另外三项人家不管怎么变都没有改变原点O(0,0)原点O(0, 0)原点O(0,0)的位置)。直接在三维中不好求解,升维后非常 "便于计算"。
- 通常假设经过变换矩阵 后的点为 (x′,y′,z′,1)(x',y',z',1)(x′,y′,z′,1),也就是固定维度w=1w = 1w=1 的三维空间。类比理解三维空间中固定其中一个维度的数值,其意义就是一个平面,例如固定ZZZ后就能得到无数的点(x,y,z)→(x,y)(x,y,z)\rightarrow(x,y)(x,y,z)→(x,y)构成的平面OXY平面OXY平面OXY,而这个动作叫 "投影" ------ 高维度向低维度的投影。我们不必关心高维如何变化什么意义,只需要知道它可以求得我们渴求的变化结果 (x′,y′,z′)(x',y',z')(x′,y′,z′),至于什么 "投影" 概念一边凉快儿去!
(i⃗,j⃗,k⃗,l⃗)=[i1j1k1Δxi2j2k2Δyi3j3k3Δzi4j4k41]\begin{align*} \begin{pmatrix} \vec{i}, \vec{j}, \vec{k}, \vec{l} \end{pmatrix} &= \begin{bmatrix} i_1 & j_1 & k_1 & \Delta x \\ i_2 & j_2 & k_2 & \Delta y \\ i_3 & j_3 & k_3 & \Delta z \\ i_4 & j_4 & k_4 & 1 \\ \end{bmatrix} \end{align*} (i ,j ,k ,l )= i1i2i3i4j1j2j3j4k1k2k3k4ΔxΔyΔz1
多项式
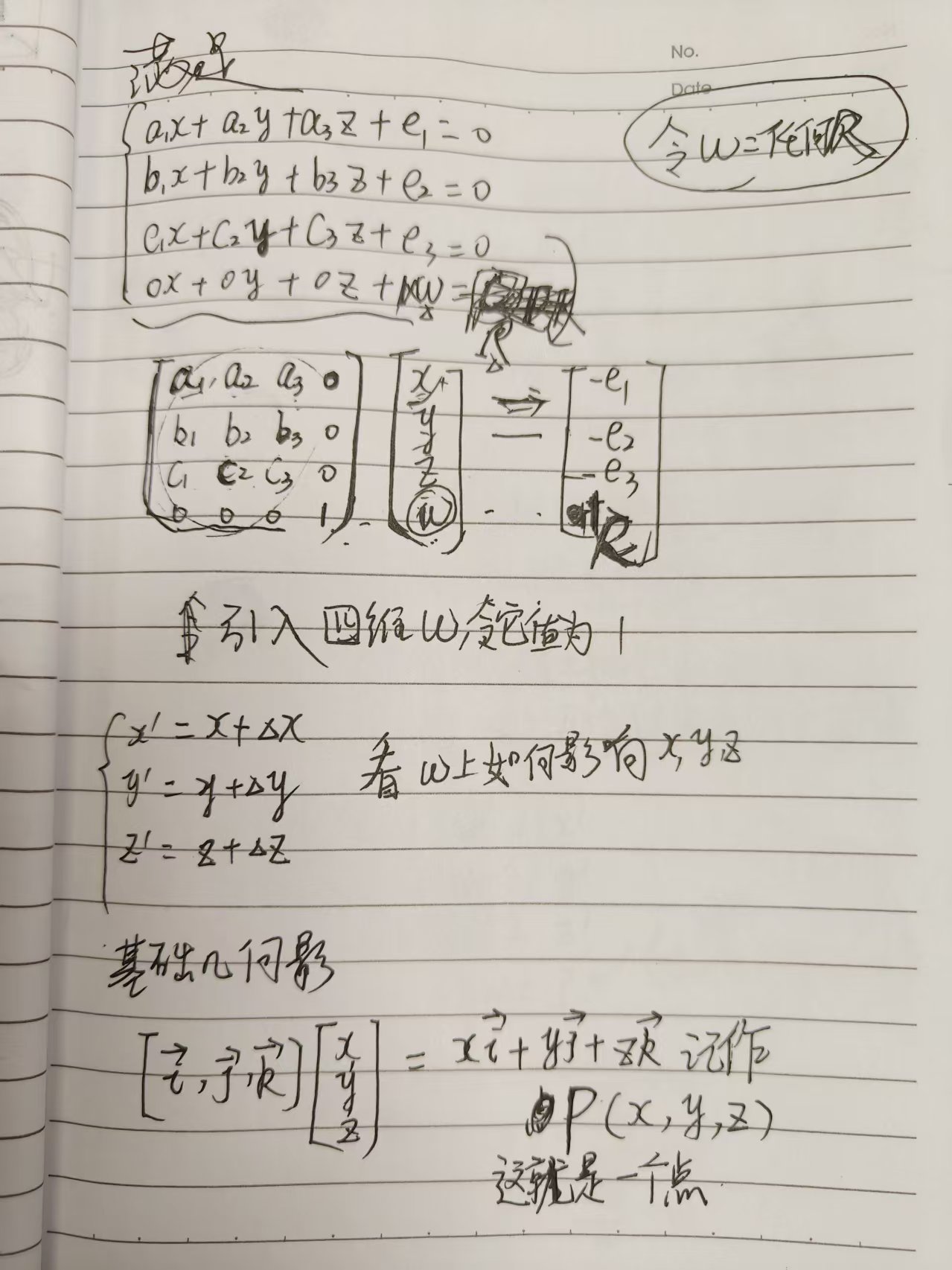
- 多元一次方程组(一次多项式)
- 多项式拓展(w∈Rw \in \Rw∈R)变量,几何意义类比
二维平面、三维立体相当于**"空间维度升了一维"**,因为我们主动添加了 维度(w)维度(w)维度(w), 即使什么都不考虑吧,那你让它等于几都可以呀,因为你甩出了魔法🪄 0x+0y+0z+1w=R0x + 0y + 0z + 1w = \R0x+0y+0z+1w=R, 然后令(w=1w = 1w=1)这个式子写作 0x+0y+0z+1×(w为1)=10x + 0y + 0z + 1\times(w 为 1) = 10x+0y+0z+1×(w为1)=1
矩阵
😓草稿,很多错误例如(多项式一元方程组) 应为 多元一次方程组---多项式
忽略 页面顶部的"行列式",瞎写的草稿,作者本人已经 6年 没碰线性代数了, 早就忘了什么乱七八糟的概念。只是记得一些 形式化的东西和定义 , 例如 等号两边加同样的东西,等号仍然成立。
