day22 哈希表和二叉树

哈希表

概念

存放记录数组，主要实现查找的功能

哈希函数

取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址
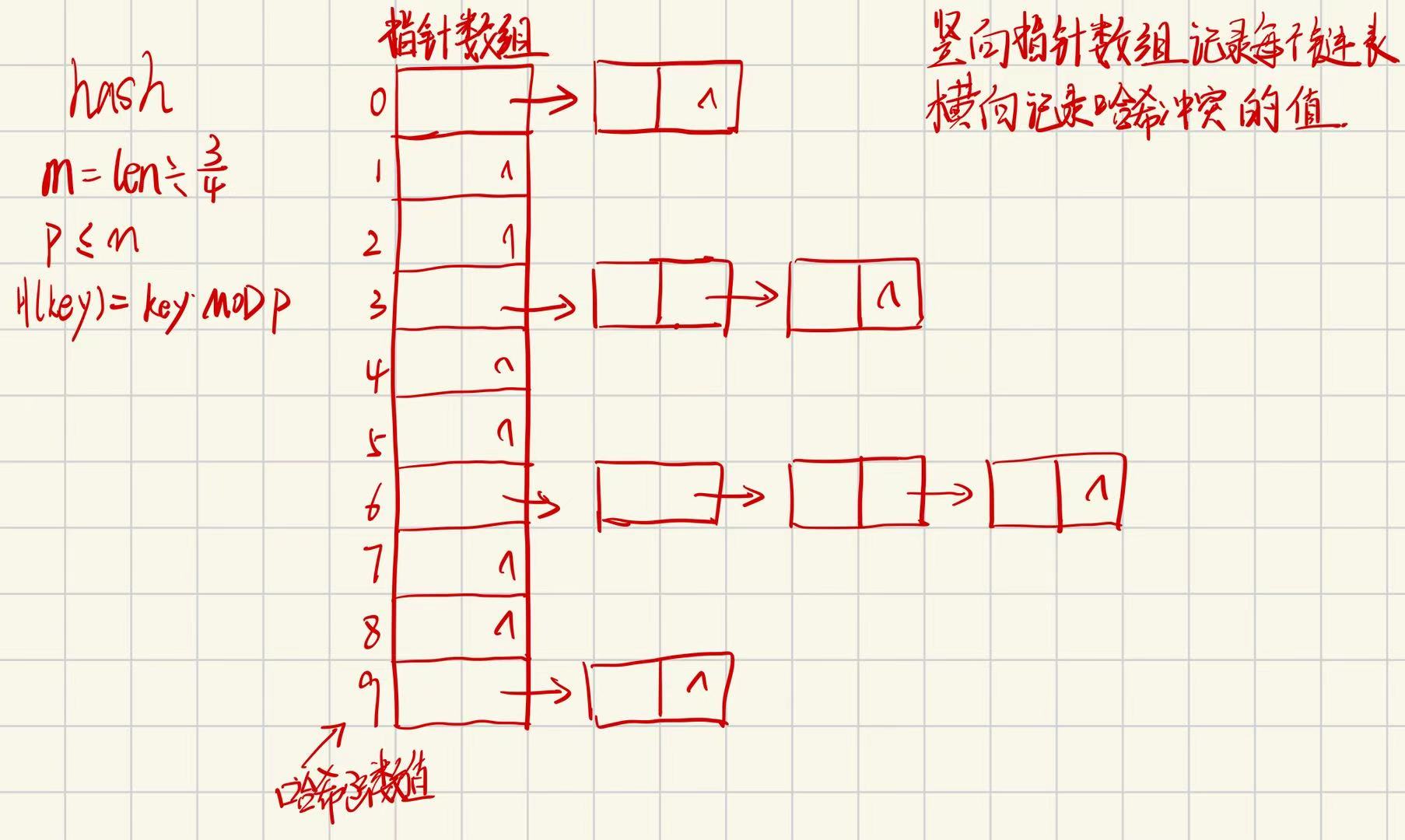
H(key)=key MOD p , p≤m

m为数组长度除以3/4 即m=len*4/3

p为小于等于m的最小素数

哈希冲突

将所有哈希函数值相同的记录存储在同一线性表

图示

哈希表代码相关函数

链表的结构

复制代码

//链表结构
typedef struct node 
{
	union
	{
		int len;
		int data;
	};
	struct node *next;
}node,*node_ptr;

节点创建

node_ptr link_create(int n)

函数功能：创建头节点和其他节点

参数：n决定创建头节点还是其他节点

返回值：创建节点地址

复制代码

    node_ptr p=(node_ptr)malloc(sizeof(node));
	if(p==NULL)
	{
		return NULL;
	}
	//创建成功
	if(n==0)
	{
		p->len=0;
	}
	else if(n==1)
	{
		p->data=0;
	}
	p->next=NULL;
	return p;

素数判定

int prime(int m)

函数功能：求出小于m的最大素数

参数：m 哈希表长度

返回值：p 最大素数

外循环遍历小于m的数，内循环遍历整除，当不能整除即为找到素数

复制代码

for(int i=m;i>2;i--)
{
	int conut=0;
	for(int j=2;j<sqrt(i);j++)
	{
		if(i%j==0)
		conut++;
	}
	if(conut==0)
	return i;
}

插入到哈希表

void insert_head(int key,node_ptr hash\[\],int m)

函数功能：将数值通过哈希函数确定位置后插入到哈希表内

参数：数值，哈希表，哈希表长度

返回值：无

复制代码

    //哈希函数
	int p=prime(m);
	int sub=key%p;
	//将key插入到hash[sub]
	node_ptr head=hash[sub];
	//创建新节点
	node_ptr s=link_create(1);
	s->data=key;
	//头插
	s->next=head->next;
	head->next=s;
	//长度自增
	head->len++;

哈希表遍历

void hash_show(node_ptr hash\[\],int m)

函数功能：遍历哈希表的值

参数：哈希表，哈希表长度

返回值：无

复制代码

void hash_show(node_ptr hash[],int m)
{
	for(int i=0;i<m;i++)
	{
		printf("%d::",i);
		node_ptr p=hash[i]->next;
		while(p!=NULL)
		{
			printf("%-4d",p->data);
			p=p->next;
		}
		printf("NULL\n");
	}

}

哈希表查找

void seach(int key,node_ptr hash\[\],int m)

函数功能：哈希表的查找值

参数：值，哈希表，哈希表长度

返回值：无

通过哈希函数确实查找元素所在的行，再遍历行链表

复制代码

void seach(int key,node_ptr hash[],int m)
{
	int p=prime(m);
	//哈希函数
	int sub=key%p;
	node_ptr pa=hash[sub]->next;
	while(pa!=NULL)
	{
		if(pa->data==key)
		{
			printf("查找元素存在\n");
			return ;
		}
		pa=pa->next;
	}
	printf("查找元素不存在\n");
}

完整代码

复制代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
//链表结构
typedef struct node 
{
	union
	{
		int len;
		int data;
	};
	struct node *next;
}node,*node_ptr;
//节点创建
node_ptr link_create(int n)
{
	node_ptr p=(node_ptr)malloc(sizeof(node));
	if(p==NULL)
	{
		return NULL;
	}
	//创建成功
	if(n==0)
	{
		p->len=0;
	}
	else if(n==1)
	{
		p->data=0;
	}
	p->next=NULL;
	return p;
}
//素数判定函数
int prime(int m)
{
	for(int i=m;i>2;i--)
	{
		int conut=0;
		for(int j=2;j<sqrt(i);j++)
		{
			if(i%j==0)
			{
				conut++;
			}

		}
	if(conut==0)
		return i;
	}

}
//插入到哈希表
void insert_head(int key,node_ptr hash[],int m)
{
	//哈希函数
	int p=prime(m);

	int sub=key%p;

	//将key插入到hash[sub]
	node_ptr head=hash[sub];

	//创建新节点
	node_ptr s=link_create(1);
	s->data=key;

	//头插
	s->next=head->next;
	head->next=s;
	//长度自增
	head->len++;
}
void hash_show(node_ptr hash[],int m)
{
	for(int i=0;i<m;i++)
	{
		printf("%d::",i);
		node_ptr p=hash[i]->next;
		while(p!=NULL)
		{
			printf("%-4d",p->data);
			p=p->next;
		}
		printf("NULL\n");
	}

}
void seach(int key,node_ptr hash[],int m)
{
	int p=prime(m);
	//哈希函数
	int sub=key%p;
	node_ptr pa=hash[sub]->next;
	while(pa!=NULL)
	{
		if(pa->data==key)
		{
			printf("查找元素存在\n");
			return ;
		}
		pa=pa->next;
	}
	printf("查找元素不存在\n");
}
int main(int argc, const char *argv[])
{		
	//创建数组
	int arr[]={25,51,8,22,26,67,11,16,54,41};
	//创建一个哈希表
	int len=sizeof(arr)/sizeof(arr[0]);
	int m=len*4/3;   
	//先创建一个指针数组记录头节点的地址   
	node_ptr hash[m];
	for(int i=0;i<m;i++)	
	{
		hash[i]=link_create(0);
	}
	//再创建链表,将数组元素放入哈希表内
	for (int i=0;i<len;i++)
	{
		//插入元素
		insert_head(arr[i],hash,m);
	}	
	//遍历哈希表
	hash_show(hash,m);
	//哈希查找
	printf("请输入key值");
	int key;
	scanf("%d",&key);
	seach(key,hash,m);
	return 0;
}

树

二叉树的性质

1.在非空二叉树的第i层上，至多有2^(i-1)个结点(i>=1)

【1,2^(i-1)】

2.在深度为K的二叉树上总结点最多有(2^k)-1个结点（k>=1)

二叉树： $k,(2\^k)-1$

完全二叉树： $2\^(k-1), (2\^k)-1$

3.在任意一棵二叉树中，叶子结点的数目比度数为2的结点的数目多1

总节点=树杈数+1

二叉树代码

复制代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef struct node
{
	char data;
	struct node *lchild;
	struct node *rchild;

}node,*node_ptr;
//节点创建
node_ptr node_create()
{
	node_ptr p=(node_ptr)malloc(sizeof(node));
	if(NULL==p)
	return NULL;
	//初始化
	p->data=0;
	p->lchild=NULL;
	p->rchild=NULL;
}
//二叉树的创建
node_ptr tree_create()
{
	char e;
	printf("请输入字符\n");
	scanf(" %c",&e);
	if('#'==e)
	return NULL;
	//创建节点
	node_ptr tree=node_create();
	tree->data=e;
	//左孩子节点
	tree->lchild=tree_create();
	//右孩子节点
	tree->rchild=tree_create();
	return tree;
}
void first_out(node_ptr tree)
{
	if(tree==NULL)
	return ;
	//根左右
	printf("%c",tree->data); //根
	first_out(tree->lchild); //左
	first_out(tree->rchild); //右
}
void temp_out(node_ptr tree)
{
	if(tree==NULL)
	return ;
	//左根右
	first_out(tree->lchild); //左
	printf("%c",tree->data); //根
	first_out(tree->rchild); //右
}
void last_out(node_ptr tree)
{
	if(tree==NULL)
	return ;
	//左右根
	first_out(tree->lchild); //左
	first_out(tree->rchild); //右
	printf("%c",tree->data); //根
}
void count(node_ptr tree,int *n0,int *n1,int *n2)
{
	if(tree==NULL)
	return ;
	//左右
	count(tree->lchild,n0,n1,n2); //左
	count(tree->rchild,n0,n1,n2); //右
	if(tree->lchild==NULL &&tree->rchild==NULL )
		++*n0;
	else if(tree->lchild!=NULL&& tree->rchild!=NULL )
		++*n2;
	else
		++*n1;
}
int main(int argc, const char *argv[])
{		
	node_ptr tree=tree_create();
	//打印二叉树
	//先序便利
	first_out(tree);
	putchar(10);
	//中序
	temp_out(tree);
	putchar(10);
	//后序
	last_out(tree);
	putchar(10);
	//计算
	int n0=0,n1=0,n2=0;
	count(tree,&n0,&n1,&n2);
	printf("n0=%d n1=%d n2=%d\n",n0,n1,n2);
	return 0;
}