深度学习(鱼书)day06--神经网络的学习(后两节)

一、梯度
像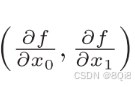
这样的由全部变量的偏导数汇总而成的向量 称为梯度(gradient)。
梯度实现的代码:
python
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # 生成和x形状相同的数组
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h)的计算
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h)的计算
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
return grad这里我们求点(3,4)、(0,2)、(3,0)处的梯度。
python
numerical_gradient(function_2, np.array([3.0, 4.0]))
# array([ 6., 8.])
numerical_gradient(function_2, np.array([0.0, 2.0]))
# array([ 0., 4.])
numerical_gradient(function_2, np.array([3.0, 0.0]))
# array([ 6., 0.])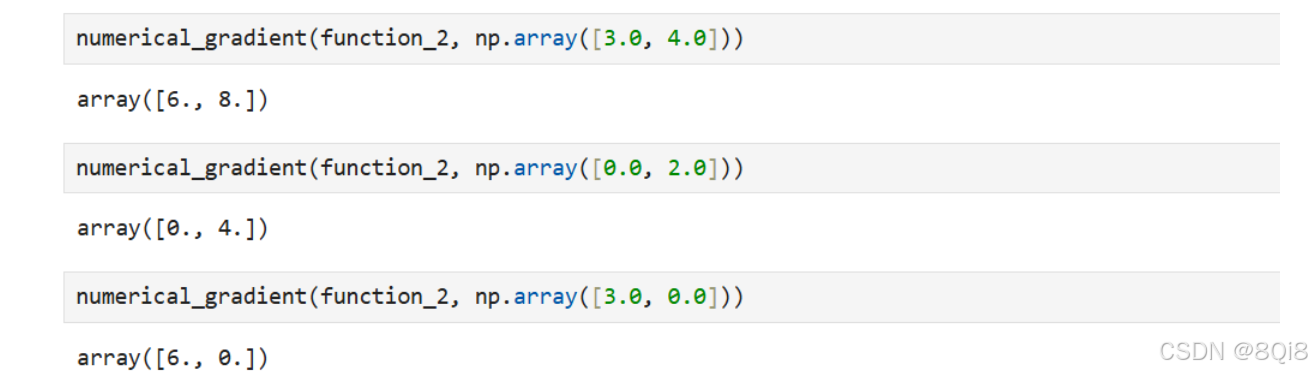
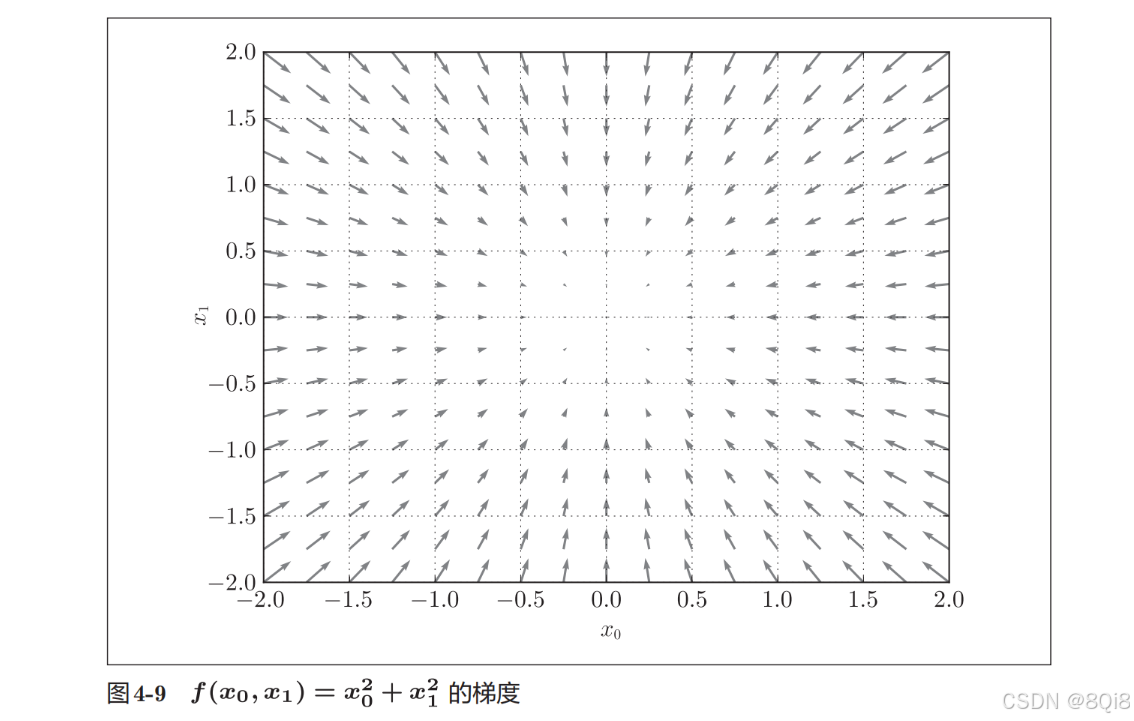
这里我们画的是元素值为负梯度的向量,梯度指向函数f(x0,x1)的"最低处 "(最小 值),就像指南针一样,所有的箭头都指向同一点。其次,我们发现离"最低处"越远,箭头越大。
梯度会指向各点处的函数值降低的方向。更严格地讲,梯度指示的方向是各点处的函数值减小最多的方向 。在复杂的函数中,梯度指示的方向基本上都不是函数值最小处。
-
梯度法:通过不断地沿梯度方向前进,逐渐减小函数值的过程就是梯度法(gradient method)
-
函数的极小值、最小值以及被称为鞍点(saddle point)的地方,梯度为 0。虽然梯度法是要寻找梯度为 0的地方,但是那个地方不一定就是最小值(也有可能是极小值或者鞍点)。当函数很复杂且呈扁平状时,学习可能会进入一个(几乎)平坦的地区,陷入被称为"学习高原"的无法前进的停滞期。
-
虽然梯度的方向并不一定指向最小值,但沿着它的方向能够最大限度地减小函数的值 。因此,在寻找函数的最小值(或者尽可能小的值)的位置的任务中,要以梯度的信息为线索,决定前进的方向。
-
寻找最小值的梯度法称为梯度下降法(gradient descent method),寻找最大值的梯度法称为梯度上升法(gradient ascent method)。 但是 通过反转损失函数的符号, 求最小值的问题和求最大值的问题会变成相同的问题,因此"下降"还是"上升"的差异本质上并不重要。一般来说,神经网络(深度学习)中,梯度法主要是指梯度下降法。
数学式子表示梯度法:
x0=x0−η∂f∂x0x1=x1−η∂f∂x1 x_0 = x_0 - \eta \frac{\partial f}{\partial x_0} \\ x_1 = x_1 - \eta \frac{\partial f}{\partial x_1} x0=x0−η∂x0∂fx1=x1−η∂x1∂f
η 表示更新量,在神经网络的学习中,称为学习率(learning rate)。学习率决定在一次学习中,应该学习多少,以及在多大程度上更新参数。这表示更新一次的式子,这个步骤会反复执行,逐渐减小函数值。在神经网络的学习中,一般会一边改变学习率的值,一边确认学习是否正确进行了。
pythondef gradient_descent(f,init_x,lr=0.01,step_sum=100): x = init_x for i in range(step_num): grad = numerical_gradient(f, x) x -= lr * grad return x参数f是要进行最优化的函数,init_x是初始值,lr是学习率learning rate,step_num是梯度法的重复次数。
-
python
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2,init_x,lr=0.1,step_num=100)
原点处是最低的地方,函数的取值一点点在向其靠近。
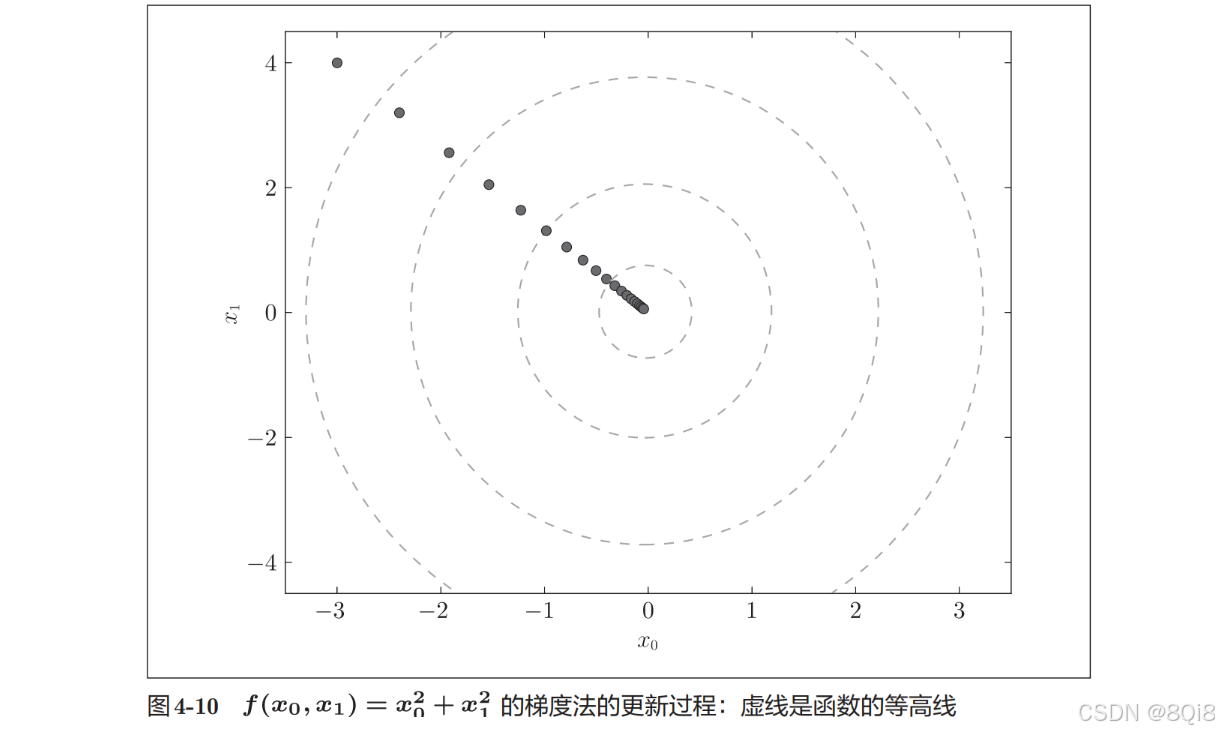
学习率过大或者过小都无法得到好的结果。我们来做个实验验证一下。
学习率过大的例子:lr=10.0
python
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=10.0, step_num=100)
# array([ -2.58983747e+13, -1.29524862e+12])学习率过小的例子:lr=1e-10
python
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=1e-10, step_num=100)
# array([-2.99999994, 3.99999992])实验结果表明,学习率过大的话,会发散成一个很大的值;反过来,学习率过小的话,基本上没怎么更新就结束了。
像学习率这样的参数称为超参数 。这是一种和神经网络的参数(权重和偏置)性质不同的参数。相对于神经网络的权重参数是通过训练数据和学习算法自动获得的,学习率这样的超参数则是人工设定的 。一般来说,超参数需要尝试多个值,以便找到一种可以使学习顺利进行的设定。
-
神经网络的梯度
神经网络的学习也要求梯度,这里所说的梯度是指损失函数关于权重参数的梯度:
\\boldsymbol{W} = \\begin{pmatrix} w_{11} \& w_{12} \& w_{13} \\ w_{21} \& w_{22} \& w_{23} \\end{pmatrix} \\ \\frac{\\partial L}{\\partial \\boldsymbol{W}} = \\begin{pmatrix} \\frac{\\partial L}{\\partial w_{11}} \& \\frac{\\partial L}{\\partial w_{12}} \& \\frac{\\partial L}{\\partial w_{13}} \\ \\frac{\\partial L}{\\partial w_{21}} \& \\frac{\\partial L}{\\partial w_{22}} \& \\frac{\\partial L}{\\partial w_{23}} \\end{pmatrix}
我们以一个简单的神经网络为例,来实现求梯度的代码:
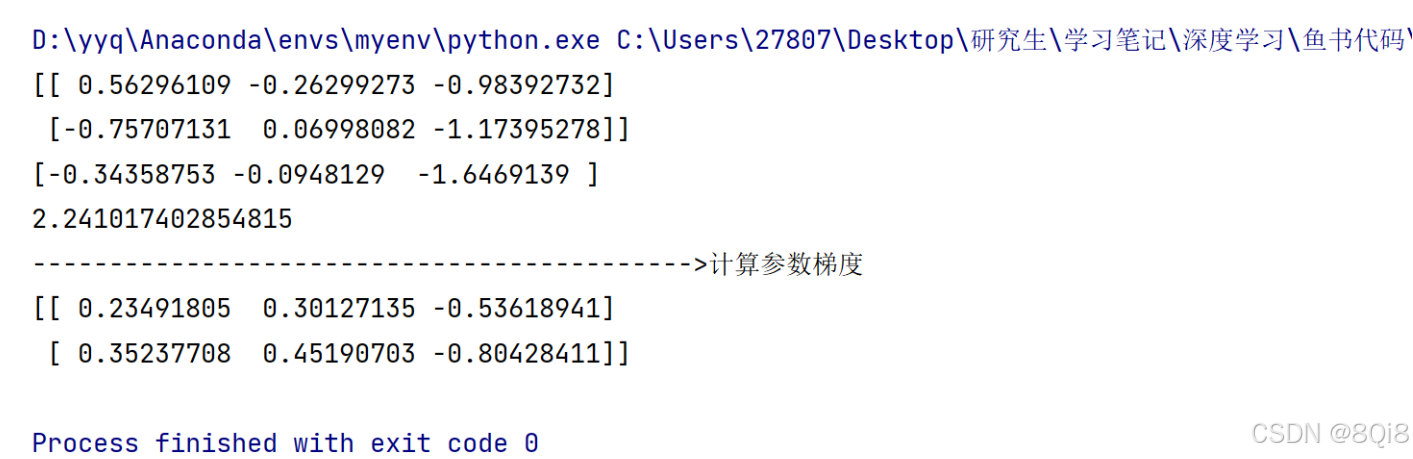
pythonimport sys, os sys.path.append(os.pardir) # 为了导入父目录中的文件而进行的设定 import numpy as np from common.functions import softmax, cross_entropy_error from common.gradient import numerical_gradient class simpleNet: def __init__(self): self.W = np.random.randn(2, 3) def pridect(self,x): return np.dot(x,self.W) def loss(self,x,t): z = self.pridect(x) y = softmax(z) loss = cross_entropy_error(y, t) return loss net = simpleNet() print(net.W) x = np.array([0.6, 0.9]) p = net.pridect(x) print(p) t = np.array([0, 0, 1]) loss = net.loss(x, t) print(loss) print("------------------------------------------->计算参数梯度") # def f(W): # return net.loss(x, t) f = lambda w: net.loss(x, t) dW = numerical_gradient(f, net.W) print(dW)
二、学习算法的实现
神经网络的学习步骤:
前提
神经网络存在合适的权重和偏置,调整权重和偏置以便拟合训练数据的过程称为"学习"。神经网络的学习分成下面4个步骤。
步骤1(mini-batch)
从训练数据中随机选出一部分数据,这部分数据称为mini-batch。我们的目标是减小mini-batch的损失函数的值。
步骤2(计算梯度)
为了减小mini-batch的损失函数的值,需要求出各个权重参数的梯度。梯度表示损失函数的值减小最多的方向。
步骤3(更新参数)
将权重参数沿梯度方向进行微小更新。
步骤4(重复)
重复步骤1、步骤2、步骤3。
这里使用的数据是随机选择的mini batch 数据,所以又称为随机梯度下降法(stochastic gradient descent )。"随机"指的是"随机选择的"的意思,随机梯度下降法是"对随机选择的数据进行的梯度下降法"。深度学习的很多框架中,随机梯度下降法一般由一个名为SGD的函数来实现。SGD来源于随机梯度下降法的英文名称的首字母。
我们来实现手写数字识别的神经网络。这里以2层神经网络(隐藏层为1层的网络)为对象,使用MNIST数据集进行学习。
-
2层神经网络的类
pythonimport sys, os sys.path.append(os.pardir) from common.functions import * from common.gradient import numerical_gradient class TwoLayerNet: def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01): self.params = {} self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size) self.params['b1'] = np.zeros(hidden_size) self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b2'] = np.zeros(output_size) def predict(self, x): W1, W2 = self.params['W1'],self.params['W2'] b1, b2 = self.params['b1'],self.params['b2'] a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 y = softmax(a2) return y def loss(self, x, t): y = self.predict(x) return cross_entropy_error(y, t) def accuracy(self, x, t): y = self.predict(x) y = np.argmax(y, axis=1) t = np.argmax(t, axis=1) accuracy = np.sum(y == t) / float(x.shape[0]) return accuracy def numerical_gradient(self, x, t): loss_w = lambda w: self.loss(x, t) grads = {} grads['W1'] = numerical_gradient(loss_w, self.params['W1']) # 这里的numerical_gradient()是之前定义的求数值微分的函数 grads['b1'] = numerical_gradient(loss_w, self.params['b1']) grads['W2'] = numerical_gradient(loss_w, self.params['W2']) grads['b2'] = numerical_gradient() def gradient(self, x, t): W1, W2 = self.params['W1'], self.params['W2'] b1, b2 = self.params['b1'], self.params['b2'] grads = {} batch_num = x.shape[0] a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 y = softmax(a2) dy = (y - t) / batch_num grads['W2'] = np.dot(z1.T, dy) grads['b2'] = np.sum(dy, axis=0) da1 = np.dot(dy, W2.T) dz1 = sigmoid_grad(a1) * da1 grads['W1'] = np.dot(x.T, dz1) grads['b1'] = np.sum(dz1, axis=0) return grads

-
mini-batch的实现
所谓mini-batch学习,就是从训练数据中随机选择一部分数据(称为mini-batch),再以这些mini-batch为对象,使用梯度法更新参数的过程。下面,我们就以TwoLayerNet类为对象,使用MNIST数据集进行学习。
python# coding: utf-8 import sys, os sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定 import numpy as np import matplotlib.pyplot as plt from dataset.mnist import load_mnist from two_layer_net import TwoLayerNet # 读入数据 (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True) network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10) iters_num = 10000 # 适当设定循环的次数 train_size = x_train.shape[0] batch_size = 100 learning_rate = 0.1 train_loss_list = [] for i in range(iters_num): batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 计算梯度 #grad = network.numerical_gradient(x_batch, t_batch) grad = network.gradient(x_batch, t_batch) # 更新参数 for key in ('W1', 'b1', 'W2', 'b2'): network.params[key] -= learning_rate * grad[key] loss = network.loss(x_batch, t_batch) train_loss_list.append(loss)mini-batch的大小为100,需要每次从60000个训练数据中随机取出100个数据(图像数据和正确解标签数据)。然后,对这个包含100笔数据的mini-batch求梯度,使用随机梯度下降法(SGD)更新参数。这里,梯度法的更新次数(循环的次数)为10000。每更新一次,都对训练数据计算损失函数的值,并把该值添加到数组中。
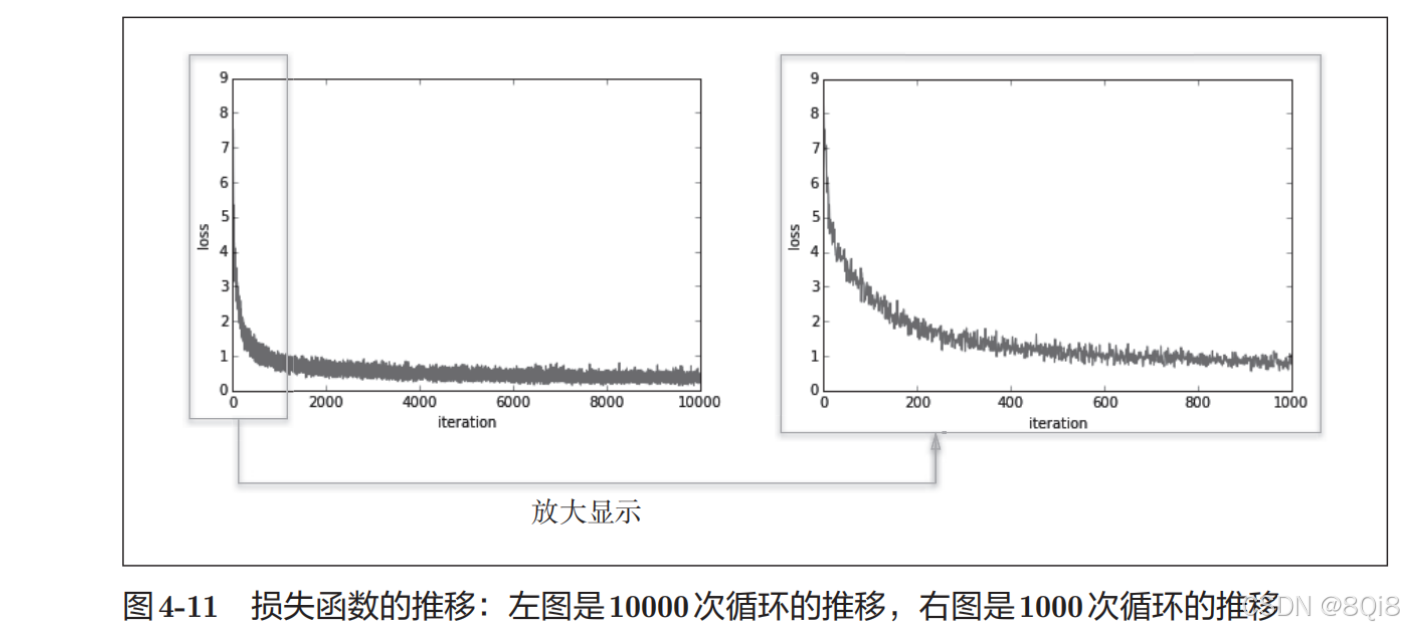
可以发现随着学习的进行,损失函数的值在不断减小。这是学习正常进行的信号,表示神经网络的权重参数在逐渐拟合数据。
-
基于测试数据的评价
神经网络的学习中,必须确认是否能够正确识别训练数据以外的其他数据,即确认是否会发生过拟合。过拟合是指,虽然训练数据中的数字图像能被正确辨别,但是不在训练数据中的数字图像却无法被识别的现象。
- epoch是一个单位。一个 epoch表示学习中所有训练数据均被使用过一次时的更新次数。比如,对于 10000笔训练数据,用大小为 100笔数据的mini-batch进行学习时,重复随机梯度下降法 100次,所有的训练数据就都被"看过"了A。此时,100次就是一个 epoch。
完善代码:
python# coding: utf-8 import sys, os sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定 import numpy as np import matplotlib.pyplot as plt from dataset.mnist import load_mnist from two_layer_net import TwoLayerNet # 读入数据 (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True) network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10) iters_num = 10000 # 适当设定循环的次数 train_size = x_train.shape[0] batch_size = 100 learning_rate = 0.1 train_loss_list = [] train_acc_list = [] test_acc_list = [] iter_per_epoch = max(train_size / batch_size, 1) for i in range(iters_num): batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 计算梯度 #grad = network.numerical_gradient(x_batch, t_batch) grad = network.gradient(x_batch, t_batch) # 更新参数 for key in ('W1', 'b1', 'W2', 'b2'): network.params[key] -= learning_rate * grad[key] loss = network.loss(x_batch, t_batch) train_loss_list.append(loss) if i % iter_per_epoch == 0: train_acc = network.accuracy(x_train, t_train) test_acc = network.accuracy(x_test, t_test) train_acc_list.append(train_acc) test_acc_list.append(test_acc) print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc)) # 绘制图形 markers = {'train': 'o', 'test': 's'} x = np.arange(len(train_acc_list)) plt.plot(x, train_acc_list, label='train acc') plt.plot(x, test_acc_list, label='test acc', linestyle='--') plt.xlabel("epochs") plt.ylabel("accuracy") plt.ylim(0, 1.0) plt.legend(loc='lower right') plt.show()
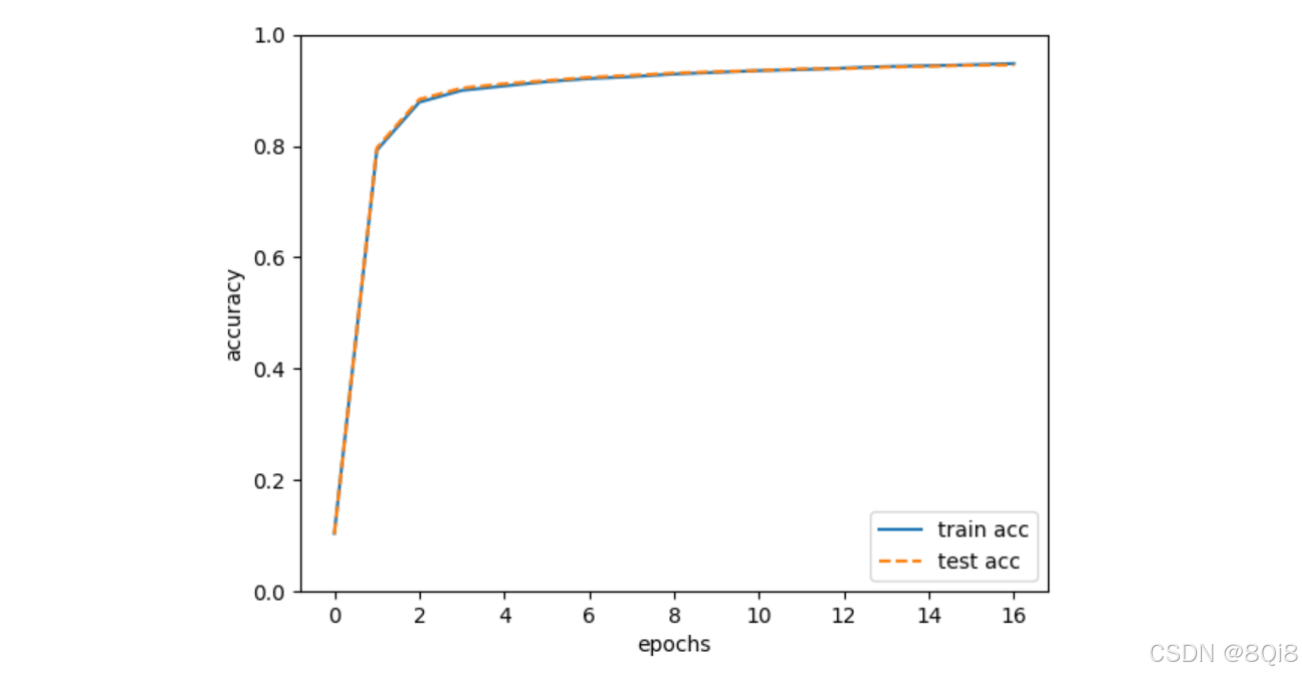
实线表示训练数据的识别精度,虚线表示测试数据的识别精度。如图所示,随着epoch的前进(学习的进行),我们发现使用训练数据和测试数据评价的识别精度都提高了,并且,这两个识别精度基本上没有差异 (两条线基本重叠在一起)。因此,可以说这次的学习中没有发生过拟合的现象。