《C++二叉搜索树原理剖析：从原理到高效实现教学》

前引：二叉搜索树（Binary Search Tree, BST）作为一种基础且强大的数据结构，凭借其高效的查找与插入效率，成为算法设计与内存优化的核心工具。在C++中，BST不仅能实现高效的数据管理，更为平衡树（如AVL树）奠定理论基础。本文将深入剖析BST的有序性本质 （结合C++特性详解插入、删除、遍历等关键操作，并提供内存安全的现代C++实现范式！

目录

【一】二叉搜索树介绍

【二】特点剖析

【三】二叉搜索树实现

（1）结构创建

（2）插入节点

（3）中序遍历

（4）查找节点

（5）删除节点

（6）析构

（7）拷贝构造

---

【一】二叉搜索树介绍

二叉搜索树又称二叉排序树，我们根据它的名字猜到是一颗二叉树完成了排序的工作？二叉树如何排序？下面我们来看看它和我们之前学习的大小顶堆有和区别！

【二】特点剖析

例如下面一棵二叉搜索树（可以为空树）：

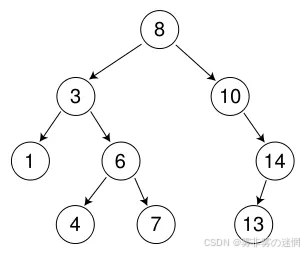
二叉搜索树语言描绘特征如下：

（1）从第一个父节点（根节点）开始，它的左子节点小于父节点

（2）从第一个父节点（根节点）开始，它的右子节点大于父节点

（3）它的左右子树也分别为二叉搜索树

【三】二叉搜索树实现

（1）结构创建

实现一棵二叉搜索树，我们需要一个节点结构、一个功能结构

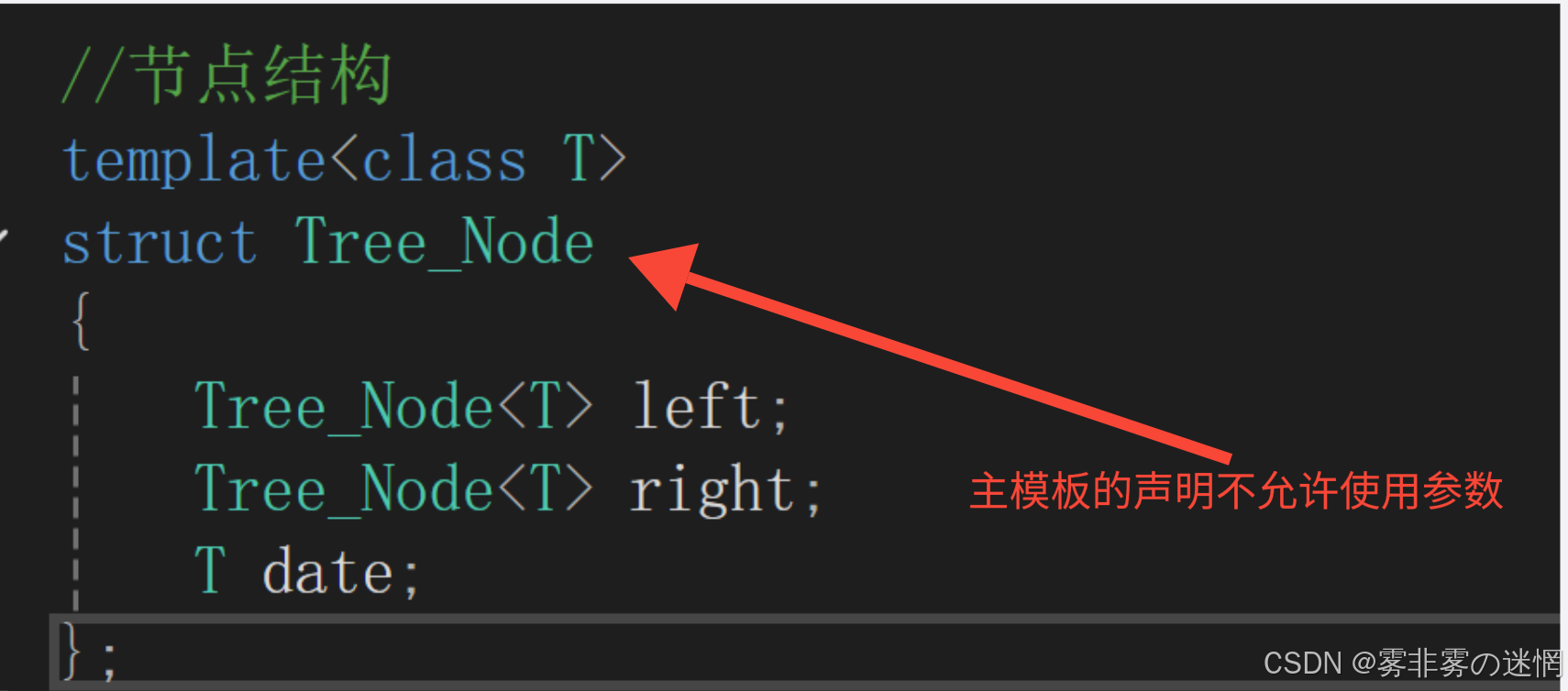
节点结构里面有左右子节点（left，right）、一个数据存储变量（date）：

//节点结构
template<class T>
struct Tree_Node
{
	Tree_Node(const T _date)
		:left(nullptr)
		,right(nullptr)
		,date(_date)
	{ }
	Tree_Node<T>* left;
	Tree_Node<T>* right;
	T date;
};

**注意：**主模板的声明不允许使用模板参数

功能结构用来实现二叉搜索树的功能：

//功能结构
template<class T>
class BST
{
	typedef Tree_Node<T> Node;
public:
	//构造
	BST()
		:node(nullptr)
	{ }

	//功能实现

private:
	Node* node;
};

（2）插入节点

插入节点我们需要根据数据的大小来判断插在左右节点的 nullptr 位置，我们这里挑战循环来写

**注意：**我们需要用其它节点代替node去移动，不然node每次都不是指向根节点的

//插入节点
void Insert(const T& date)
{
	//如果根节点为空
	if (node == nullptr)
	{
		node = new Node(date);
		return;
	}
	//根据数据大小查找
	Node* parent = nullptr;
	Node* cur = node;
	while (cur)
	{
		//记录父节点
		parent = cur;
		//如果小于父节点
		if (date < cur->date)
		{
			cur = cur->left;
		}
		else
		{
			cur = cur->right;
		}
	}
	//此时已经到了节点为空的位置
	//如果小于父节点
	if (date < parent->date)
	{
		//插在父节点左侧
		parent->left = new Node(date);
		return;
	}
	else
	{
		//插在父节点右侧
		parent->right = new Node(date);
		return;
	}
}

（3）中序遍历

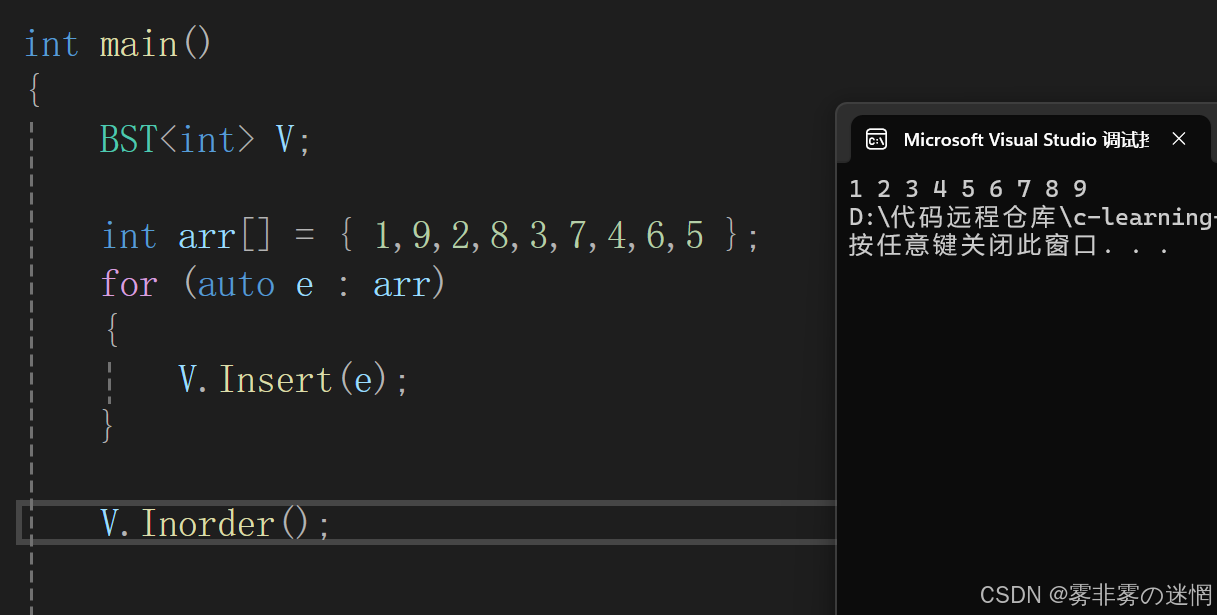
中序我们调用递归来完成：先遍历左子树，然后父节点，然后右子树

//中序遍历
void Inorder()
{
	_Inorder(node);
}
void _Inorder(Node* ptr)
{
	//遇到空就返回
	if (ptr == nullptr)
	{
		return;
	}

	_Inorder(ptr->left);

	cout << ptr->date << " ";

	_Inorder(ptr->right);
}

效果展示：

（4）查找节点

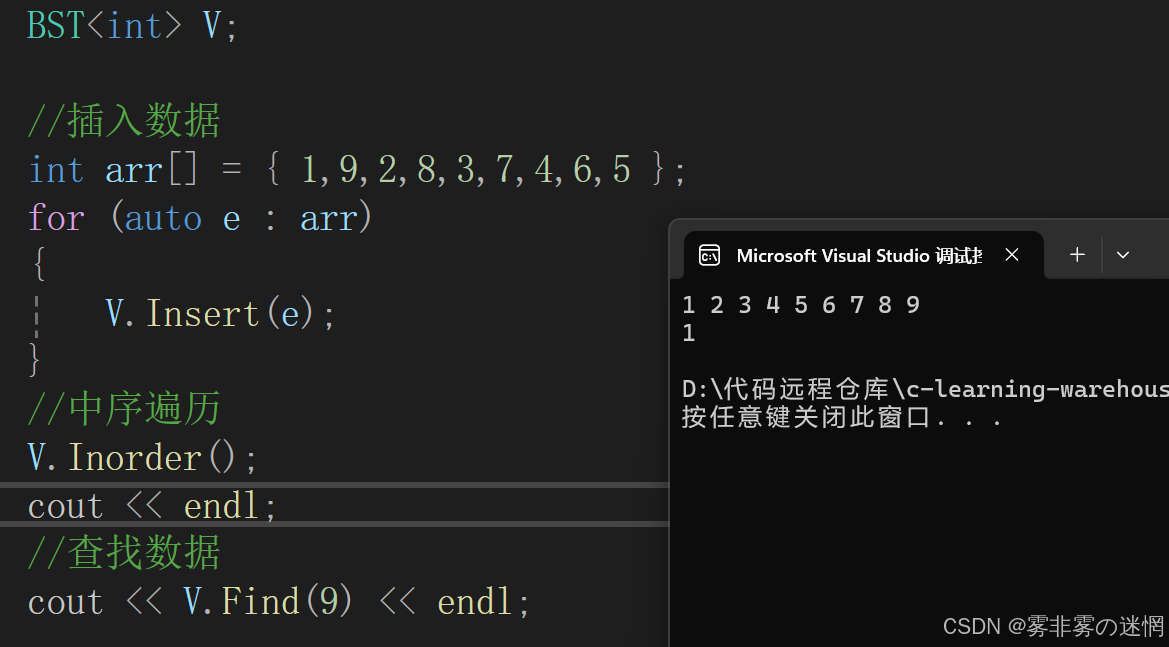
找到对应节点之后，然后返回即可：

根据要找的数据大小去查找，那么最多查找次数就是二叉树的深度次

//查找数据
bool Find(const T& date)
{
	//如果为空树，返回
	if (node == nullptr)
	{
		return false;
	}
	Node* cur = node;
	//找节点
	while (cur)
	{
		//如果date大于父节点，右边找，否则左边找
		if (date > cur->date)
		{
			cur = cur->right;
		}
		else if(date < cur->date)
		{
			cur = cur->left;
		}
		else
		{
			return true;
		}
	}
	//如果出循环了还没有返回就说明没有找到
	return false;
}

效果展示：

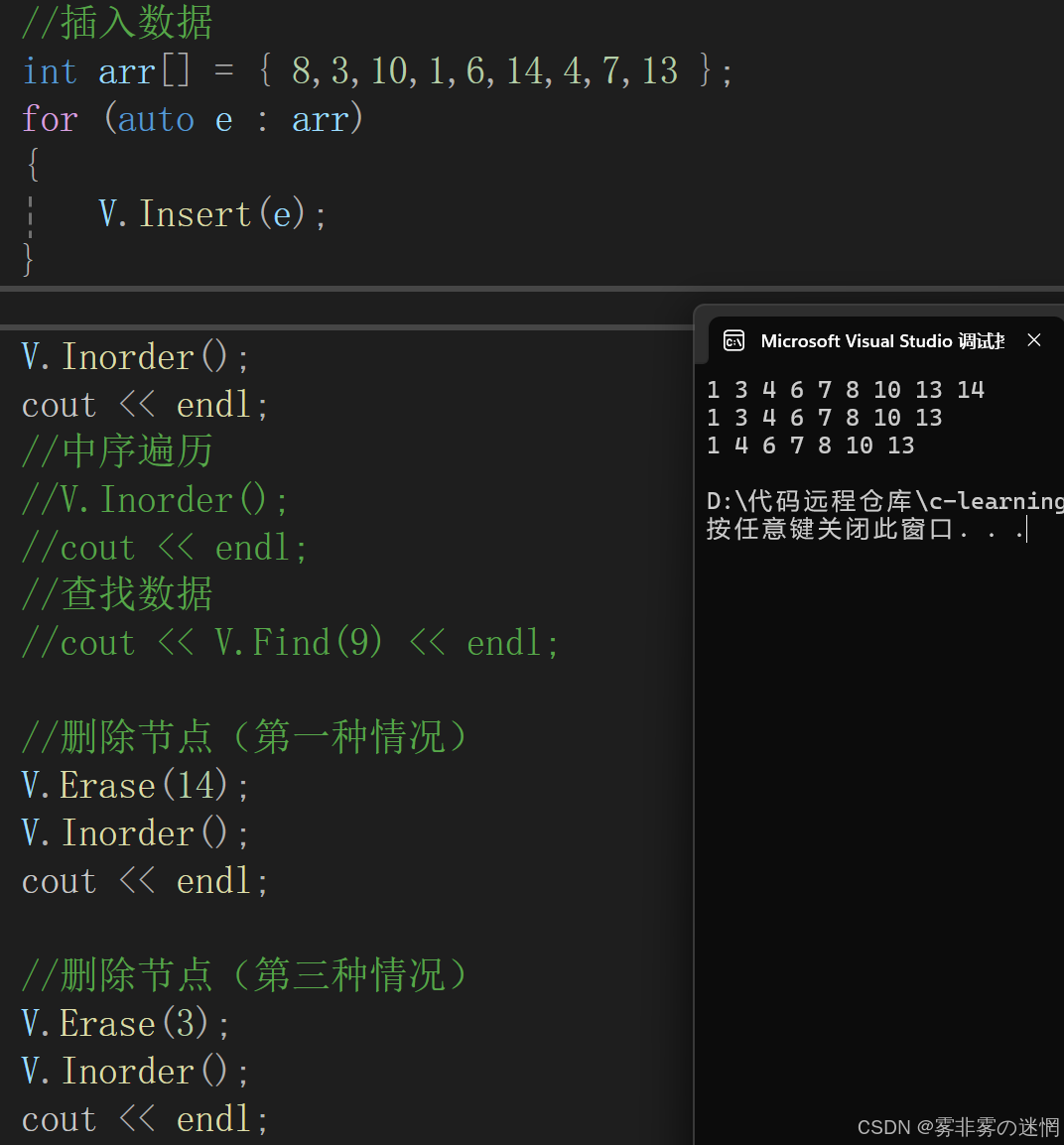
（5）删除节点

删除节点我们需要考虑下面这三个情况（重点是比较节点数据大小）：

（1）该节点无孩子节点：先删，然后置空

（2）该节点有一个孩子节点：先连接再删

**注意：**这两种情况可以概括为一类，参考下面代码注释，比较简单我们就直接看代码
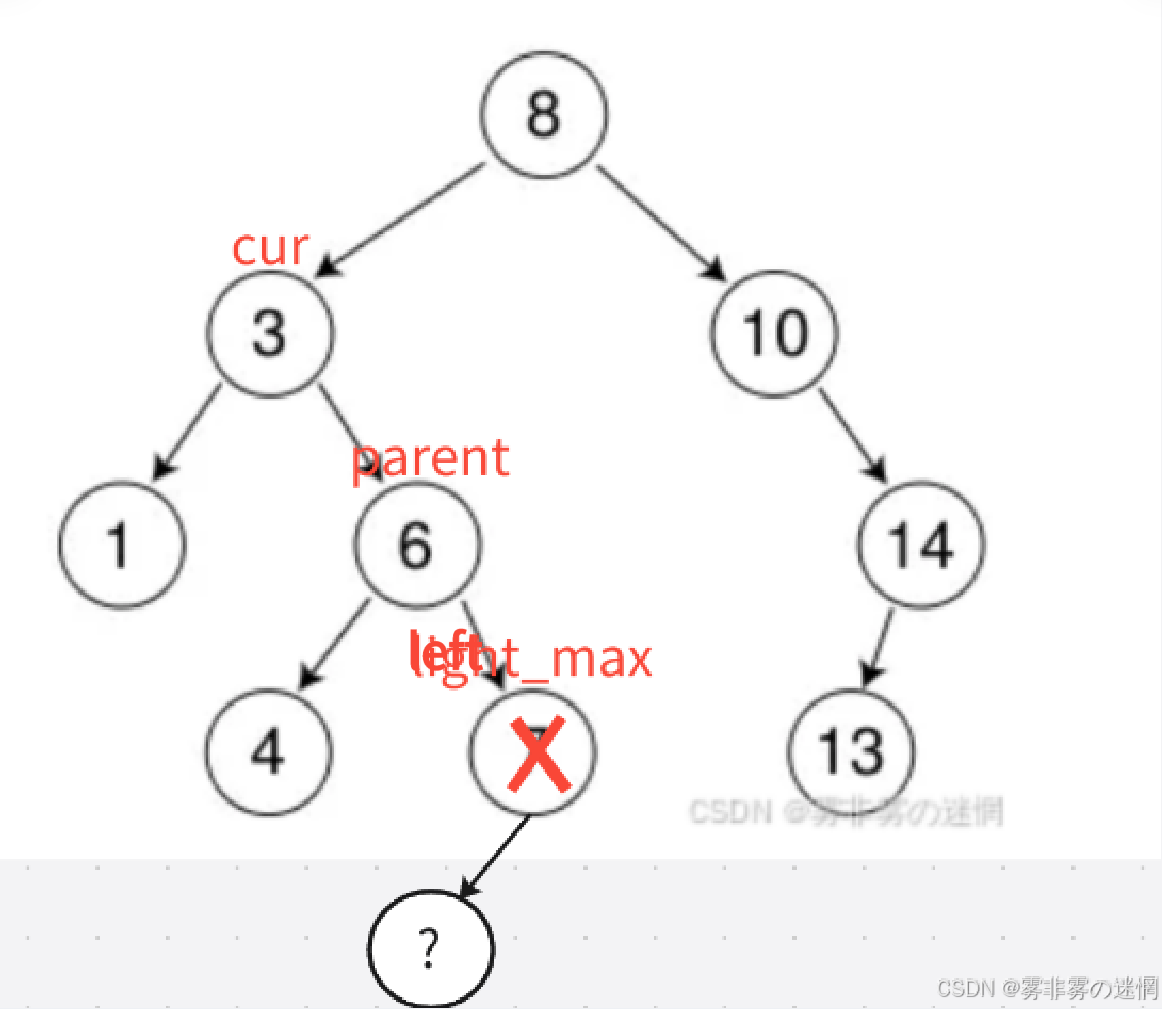
（3）该节点有两个孩子节点：我们需要找一定大小的节点去替代它

替代思路：让它的左子树最大值或者右子树最小值去替换，然后删除它（左子树max为例）

·

**解释：**例如下面这幅图，我们要删除3

（1）先找到目标节点cur（3），然后找目标节点左子树的最大值left_max

（2）交换目标节点cur和最大值 light_max的数据

（3）这里需要标记 lleft_max的父节点为 parent

第一种情况：

（4）因为找的是左子树的最大值，所以只可能父节点parent的右边还存在子节点，

将它连接在parent的右边

（5）再将cur指向 left_max，删除

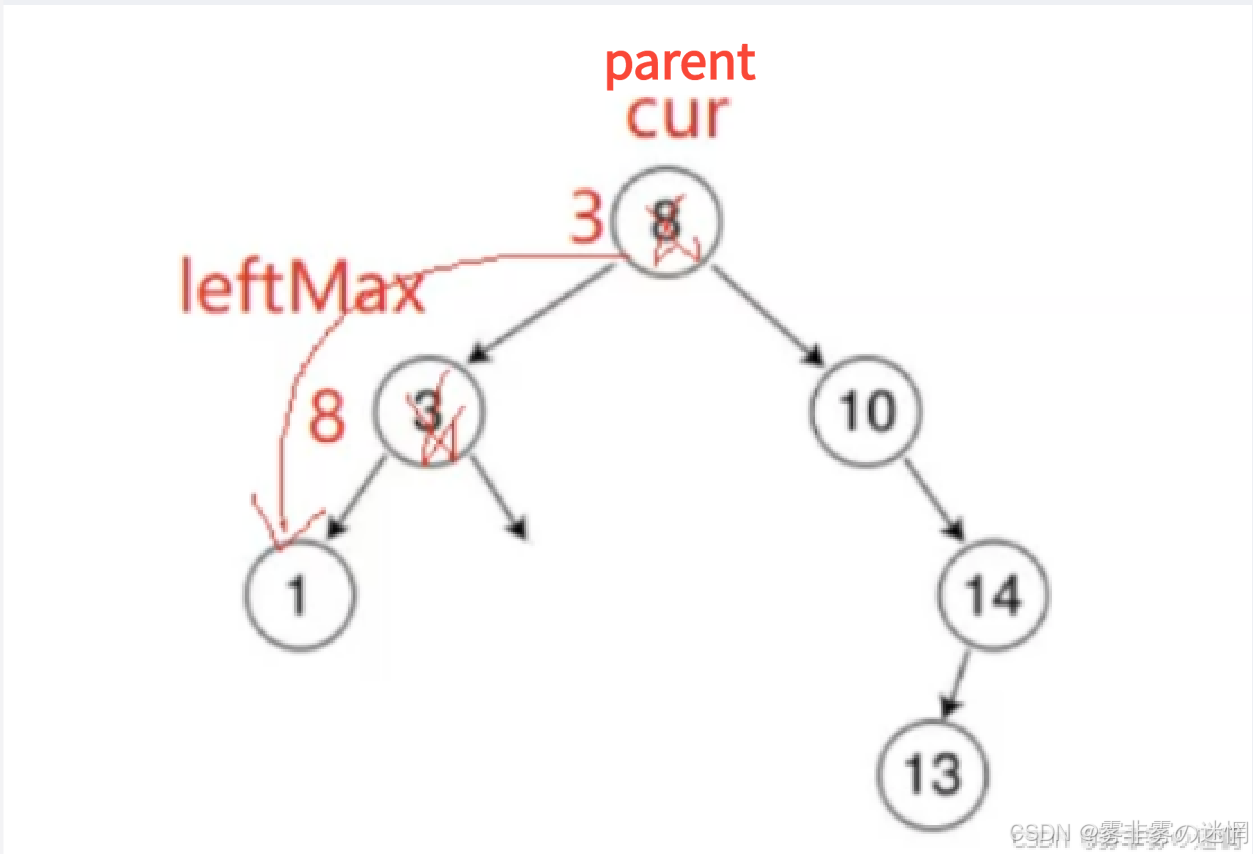
第二种情况：

（4）因为找的是左子树的最大值，可能 parent 的左边还存在子节点

（5）再将cur指向 left_max，删除

//删除节点
void Erase(const T& date)
{
	//如果为空树
	if (node == nullptr)
	{
		return;
	}
	//标记cur的父节点
	Node* cur = node;
	Node* parent = cur;
	//找节点
	while (cur->date != date)
	{
		parent = cur;
		//如果date大于父节点，右边找，否则左边找
		if (date > cur->date)
		{
			cur = cur->right;
		}
		else if (date < cur->date)
		{
			cur = cur->left;
		}
		else
		{
			break;
		}
	}
	//第一种情况：如果cur无左右节点
	//第二种情况：如果cur只有一个孩子节点
	if (cur->left == nullptr || cur->right == nullptr)
	{
		//如果parent的date小于cur的date，说明要连接在parent的右边
		if (parent->date < cur->date)
		{
			if (cur->left == nullptr)
			{
				//cur的左孩子为空，可能右孩子不为空
				parent->right = cur->right;
			}
			else
			{
				//cur的右孩子为空，可能左孩子不为空
				parent->right = cur->left;
			}
			delete cur;
			cur = nullptr;
		}
		else
		{
			//注意只有两个节点的
			if (cur == node)
			{
				//如果删树的唯一节点
				if (cur == node && cur->right == nullptr && cur->left == nullptr)
				{
					delete node;
					node = nullptr;
				}
				else if (cur->right == nullptr)
				{
					node = cur->left;
					delete cur;
					cur = nullptr;
				}
				else
				{
					node = cur->right;
					delete cur;
					cur = nullptr;
				}
				return;
			}
			if (cur->left == nullptr)
			{
				//cur的左孩子为空，可能右孩子不为空
				parent->left = cur->right;
			}
			else
			{
				//cur的右孩子为空，可能左孩子不为空
				parent->left = cur->left;
			}
			
			delete cur;
			cur = nullptr;
			
		}
	}
	else
	{
		//第三种情况：cur有两个孩子节点
		//找左子树最大的节点
		Node* left_max = cur->left;
		Node* parent = cur;
		while (left_max->right)
		{
			parent = left_max;
			left_max = left_max->right;
		}

		// 最终走到这里就是左子树的最大节点
		swap(cur->date, left_max->date);

		// 这里要再进行一次判读parent的情况，对于节点进行连接
		if (parent->left == left_max)
		{
			parent->left = left_max->left;
		}
		else
		{
			parent->right = left_max->left;
		}
		cur = left_max;

		delete cur;
		cur = nullptr;
	}
}

效果展示：

（6）析构

我们可以利用上面的"删除节点"+"根节点是否为空循环"来不断析构

**注意：**上面我们的析构是利用第三方指针cur代替node删除的，所以当二叉树只有一个根节点删除 后需要考虑置空，这样才可以利用到循环

//析构
~BST()
{
	while (node)
	{
		Erase(node->date);
		cout << "删除成功" << endl;
	}
}

测试：

（7）拷贝构造

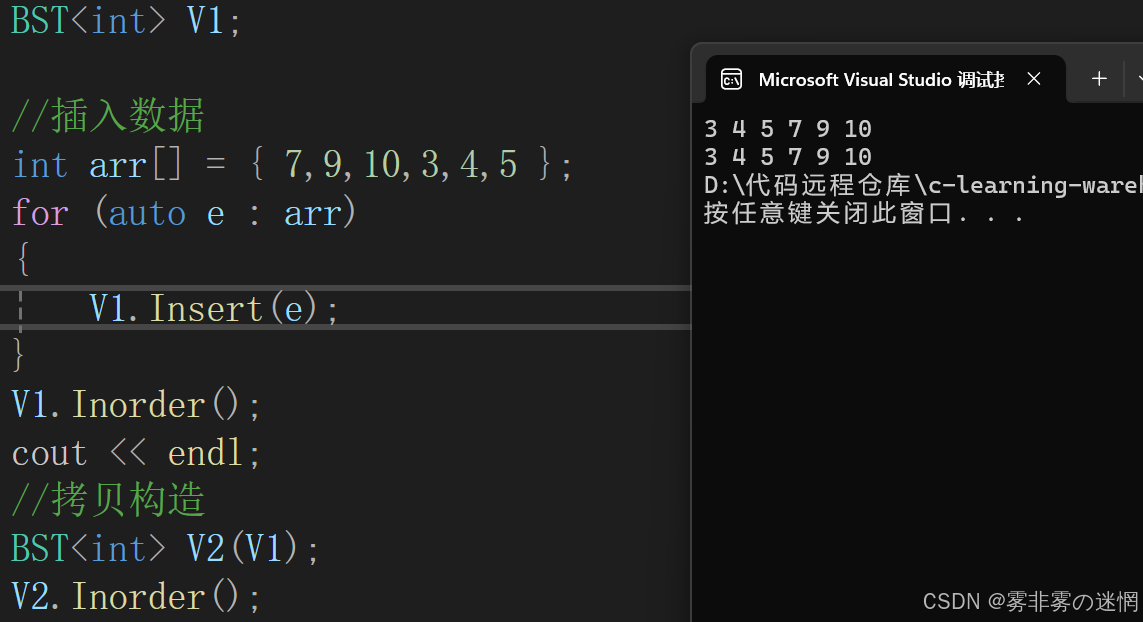
拷贝构造我们可以利用递归遍历不断开新节点

**注意：**递归左右节点时要连接起来，下面有详细的批注

//拷贝构造
BST(const BST<T>& ptr)
{
	//如果拷贝对象是空
	if (ptr.node == nullptr)
	{
		return;
	}
	//这里的ptr是拷贝的对象,node是待拷贝的对象的根节点
	node = Copy(node, ptr.node);
}


Node* Copy(Node* _node,Node* copy_node)
{
	if (copy_node == nullptr)
	{
		return nullptr;
	}
	//前序拷贝
	_node = new Node(copy_node->date);
	// 空间是开辟成功了，但是这里node的左右子树，没有连接，需要接收copy的返回值才能完成连接
	_node->left =  Copy(_node->left, copy_node->left);
	_node->right = Copy(_node->right, copy_node->right);
	//返回根节点
	return _node;
}

效果展示：