开发也能看懂的大模型：强化学习

逸风尊者2025-08-01 8:32

什么是强化学习（Reinforcement Learning，RL）？

强化学习是一种通过试错机制学习如何在环境中做出决策的机器学习方法。与监督学习不同，它没有直接的正确答案，而是通过不断与环境交互，获取奖励信号，从而逐步优化策略。

强化学习的基本概念

  1. 环境（Environment）

    系统的外部世界，强化学习的智能体与其交互。

    例如，游戏中的棋盘、自动驾驶的道路等。

  2. 智能体（Agent）

    在环境中做出决策的主体。智能体通过感知环境，执行动作并根据反馈调整行为。

    例如，自动驾驶系统、机器人。

  3. 状态（State, S）

    环境在某个时刻的描述。

    例如，棋局的布局、车辆的位置和速度。

  4. 动作（Action, A）

    智能体在当前状态下可以采取的行为。

    例如，在游戏中走一步棋，在驾驶中加速或转弯。

  5. 奖励（Reward, R）

    智能体采取某一动作后环境给出的反馈信号，用于指导智能体的学习。

    • 正奖励：鼓励当前行为。
    • 负奖励：惩罚当前行为。

  6. 策略（Policy, π）

    决定智能体在每个状态下采取哪个动作的规则或函数。

    • 确定性策略：给定状态，返回固定动作。
    • 随机策略：给定状态，返回动作的概率分布。

  7. 价值函数（Value Function, V）

    衡量在某个状态下能获得的长期回报的期望值。

    • 状态价值函数：V(s)=E[R]
    • 状态-动作价值函数：Q(s,a)

强化学习的核心思想

强化学习的目标是通过不断地试错探索 ，找到一条策略（Policy），使得智能体在与环境交互的过程中，获得的累计奖励最大化。

  1. 探索（Exploration）
    尝试新的动作，了解环境的未知部分。
    例如，在游戏中尝试不同的策略。
  2. 利用（Exploitation）
    利用已有知识，选择当前看起来最优的动作。
    例如，选择一条已知得分最高的路径。
  3. 平衡探索与利用
    在探索未知和利用已知之间权衡是强化学习中的关键问题。

强化学习的经典算法

强化学习中的经典算法主要分为两大类：基于值函数的方法 和基于策略的方法，以及两者的结合（Actor-Critic）。

以下是经典算法的讲解：

1. 基于值函数的方法

这种方法主要通过学习价值函数来间接优化策略。核心思想是计算每个状态或状态-动作对的价值，从而选择最优动作。

1.1 动态规划（Dynamic Programming, DP）

  • 适用场景：需要完整的环境模型（例如状态转移概率和奖励函数已知）。

  • 方法：

    • 值迭代（Value Iteration） ：通过迭代更新状态的价值函数 V(s) 找到最优策略。
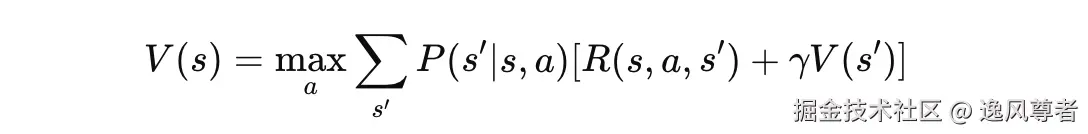
  • 策略迭代（Policy Iteration） ：交替执行策略评估和策略改进，直到收敛。

1.2 Q-Learning

  • 核心思想：使用 Q 函数 Q(s,a 表示状态 s 下采取动作 a 的长期收益，通过迭代更新找到最优 Q 函数。

  • 更新公式：

  • 优点：

    • 不需要环境模型。
    • 可以离线学习，适用于复杂环境。

  • 缺点：

    • 在高维状态空间中效率低。

1.3 SARSA（State-Action-Reward-State-Action）

  • 与 Q-Learning 类似，但更新公式使用的是当前策略生成的动作，而非最优动作：

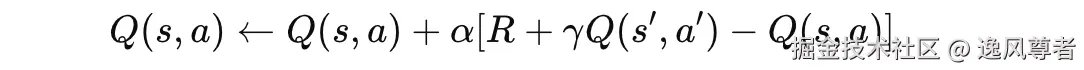
  • 区别：

    • SARSA 是 on-policy （基于当前策略学习），Q-Learning 是 off-policy（基于最优策略学习）。

2. 基于策略的方法

这种方法直接学习策略函数 π(a∣s)，而不是价值函数。

2.1 REINFORCE

  • 核心思想：通过蒙特卡洛采样，使用策略梯度方法优化策略函数。
  • 更新公式：

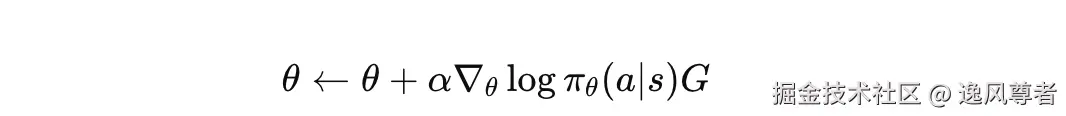其中，G 是累积奖励，θ 是策略参数。

  • 优点：适用于连续动作空间。
  • 缺点：高方差，收敛慢。

2.2 PPO（Proximal Policy Optimization）

  • 核心思想：限制策略更新的步长，防止大幅度更新导致的不稳定。

  • 优势：

    • 收敛速度快。
    • 适用于高维连续状态和动作空间。

3. Actor-Critic 方法

  • 结合值函数和策略方法的优点，使用 Actor （策略）和 Critic（价值函数）同时学习。

  • 关键思想：

    • Actor：负责生成策略 π(a∣s)。
    • Critic：负责评估策略的好坏，即计算价值函数 V(s) 或优势函数 A(s,a)。

  • 典型算法：

    • A2C（Advantage Actor-Critic） ：用优势函数 A(s,a)=Q(s,a)−V(s)代替价值函数，减少方差。
    • A3C（Asynchronous Advantage Actor-Critic） ：通过多线程并行训练提升效率。

4. 深度强化学习

使用神经网络近似值函数或策略函数，解决高维状态空间问题。

4.1 DQN（Deep Q-Network）

  • 核心思想：用神经网络近似 Q 函数。

  • 创新点：

    • 经验回放（Experience Replay） ：将交互数据存储在缓冲区中，随机采样用于训练，避免样本相关性。
    • 目标网络（Target Network） ：使用一个延迟更新的目标网络，稳定训练过程。

  • 不足：

    • 无法处理连续动作空间。

4.2 DDPG（Deep Deterministic Policy Gradient）

  • 结合 DQN 和策略梯度方法，用于连续动作空间。

  • 创新点：

    • 使用确定性策略 μ(s∣θ)。
    • 同时训练策略网络和 Q 网络。

4.3 AlphaGo / AlphaZero

  • 利用强化学习在围棋、国际象棋中实现超人类水平。

  • 方法：

    • 结合深度学习和蒙特卡洛树搜索（MCTS）。
    • 策略网络指导搜索方向，价值网络评估局面。

经典算法对比

算法 类型 特点 应用场景
值迭代/策略迭代 基于值函数 模型需已知，状态空间小 小型离散问题，如迷宫
Q-Learning 基于值函数 Off-policy，适用于离散动作空间 游戏、路径规划
SARSA 基于值函数 On-policy，更注重当前策略表现 实时交互系统
REINFORCE 基于策略 直接优化策略，适合连续动作空间 机器人控制、金融优化
PPO 基于策略 收敛稳定，计算效率高 自动驾驶、复杂决策
DQN 深度强化学习 适合高维状态空间的离散动作问题 Atari 游戏、推荐系统
DDPG 深度强化学习 连续动作空间，高效利用样本 自动驾驶、机器人控制
Actor-Critic 混合方法 减少方差，收敛快 各类强化学习场景

强化学习的应用场景

  1. 游戏

    • AlphaGo、AlphaZero 等利用强化学习在围棋、国际象棋中击败人类高手。
    • 在 Atari 游戏中实现超人类表现。

  2. 机器人控制

    • 训练机器人行走、抓取物体等复杂动作。

  3. 自动驾驶

    • 通过模拟环境训练智能驾驶策略。

  4. 推荐系统

    • 动态调整推荐策略，最大化用户点击率或留存率。

  5. 金融投资

    • 强化学习用于股票交易策略优化。

  6. 医疗

    • 优化治疗方案，如动态调整用药策略。

强化学习的挑战

  1. 样本效率低

    • 需要大量的试验数据才能学习到有效的策略。

  2. 探索与利用的权衡

    • 过多探索会导致浪费资源，过多利用会陷入次优解。

  3. 奖励稀疏或延迟

    • 当奖励信号不及时或较少时，智能体难以学习有效策略。

  4. 高维状态空间

    • 当状态和动作空间非常大时，学习变得困难。

案例分析：CartPole 平衡杆

下面通过一个经典强化学习案例------CartPole 平衡杆问题，来分析强化学习的实际应用。

案例描述：CartPole 问题

在这个问题中，一个小车（Cart）在一条直线上移动，上面平衡着一根竖直的杆（Pole）。目标是通过控制小车的左右运动，使杆尽量保持竖直状态，并防止它掉下来或小车出界。

环境设置

  • 状态空间： 包括以下 4 个变量：

    1. 小车的位置（Cart Position）。
    2. 小车的速度（Cart Velocity）。
    3. 杆的角度（Pole Angle）。
    4. 杆的角速度（Pole Angular Velocity）。

  • 动作空间：

    • 左移（Push Left）。
    • 右移（Push Right）。

  • 奖励： 每一步操作后，若杆未倒下且小车未出界，则奖励 +1。

  • 结束条件：

    1. 杆的角度超过一定阈值（例如 ±12°）。
    2. 小车超出轨道边界。
    3. 经过 200 步仍保持平衡（成功）。

强化学习方法

我们使用 深度 Q 网络（DQN） 解决 CartPole 问题。DQN 是一种结合深度学习的强化学习方法，适用于高维状态空间的问题。

解决方案

1. 环境初始化

使用 OpenAI Gym 提供的 CartPole-v1 环境：

python 复制代码 
import gym
import numpy as np
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense

# 初始化环境
env = gym.make("CartPole-v1")
state_size = env.observation_space.shape[0]  # 4维状态
action_size = env.action_space.n  # 2个动作（左移，右移）

2. 构建 Q 网络

Q 网络通过神经网络近似 Q 函数：

python 复制代码 
def build_model(state_size, action_size):
    model = Sequential([
        Dense(24, input_dim=state_size, activation="relu"),
        Dense(24, activation="relu"),
        Dense(action_size, activation="linear")  # 输出每个动作的 Q 值
    ])
    model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=0.001),
                  loss="mse")
    return model

# 创建主网络和目标网络
model = build_model(state_size, action_size)
target_model = build_model(state_size, action_size)

3. 经验回放与目标网络

经验回放用于打破样本相关性，提高训练效率：

python 复制代码 
from collections import deque

memory = deque(maxlen=2000)  # 存储交互数据
gamma = 0.95                 # 折扣因子
epsilon = 1.0                # 探索率
epsilon_min = 0.01
epsilon_decay = 0.995

# 存储交互数据
def remember(state, action, reward, next_state, done):
    memory.append((state, action, reward, next_state, done))

# 经验回放
def replay(batch_size):
    minibatch = np.random.choice(memory, batch_size, replace=False)
    for state, action, reward, next_state, done in minibatch:
        target = reward
        if not done:
            target += gamma * np.amax(target_model.predict(next_state)[0])
        target_f = model.predict(state)
        target_f[0][action] = target
        model.fit(state, target_f, epochs=1, verbose=0)

# 更新目标网络
def update_target_model():
    target_model.set_weights(model.get_weights())

4. 训练主循环

强化学习通过多次回合训练优化策略：

python 复制代码 
episodes = 1000
batch_size = 32

for e in range(episodes):
    state = env.reset()
    state = np.reshape(state, [1, state_size])
    for time in range(200):
        # ε-贪心策略
        if np.random.rand() <= epsilon:
            action = np.random.choice(action_size)
        else:
            q_values = model.predict(state)
            action = np.argmax(q_values[0])

        # 与环境交互
        next_state, reward, done, _ = env.step(action)
        next_state = np.reshape(next_state, [1, state_size])
        remember(state, action, reward, next_state, done)
        state = next_state

        # 检查是否结束
        if done:
            print(f"Episode: {e+1}/{episodes}, Score: {time}")
            break

        # 回放并更新网络
        if len(memory) > batch_size:
            replay(batch_size)
    
    # 减少探索率
    if epsilon > epsilon_min:
        epsilon *= epsilon_decay
    
    # 定期更新目标网络
    if e % 10 == 0:
        update_target_model()

案例输出分析

  • 训练初期：

    • 智能体随机探索，杆很快倒下。
    • 平均得分（即杆保持平衡的时间步数）低于 20。

  • 训练中期：

    • 随着策略的优化，杆保持平衡的时间逐渐延长。
    • ε-贪心策略使智能体逐步减少随机探索，更多利用已有策略。

  • 训练结束：

    • 智能体学会保持杆的平衡，平均得分接近或达到 200，完成任务。

结果与应用

  1. 得分趋势： 随着训练轮次增加，智能体的得分从初期的随机表现逐渐提升到接近满分。
  2. 实际意义： CartPole 问题是强化学习中的"Hello World"，类似的技术可扩展到复杂系统，如自动驾驶、机器人平衡控制等。

总结

  • CartPole 问题演示了强化学习如何通过试错和奖励机制优化策略。
  • DQN 算法成功解决了高维状态空间的问题，通过经验回放和目标网络提升了训练稳定性。
相关推荐
艾莉丝努力练剑3 分钟前
【C语言16天强化训练】从基础入门到进阶：Day 5
c语言·c++·学习·算法
尤超宇20 分钟前
基于随机森林的红酒分类与特征重要性分析
算法·随机森林·分类
花火|1 小时前
算法训练营day58 图论⑧ 拓扑排序精讲、dijkstra（朴素版）精讲
算法·图论
寒士obj1 小时前
Spring容器Bean的创建流程
java·后端·spring
掉鱼的猫1 小时前
Spring AOP 与 Solon AOP 有什么区别？
java·spring
AI_RSER1 小时前
遥感&机器学习入门实战教程｜Sklearn 案例④ ：多分类器对比（SVM / RF / kNN / Logistic...）
python·算法·机器学习·支持向量机·分类·sklearn
不是光头 强1 小时前
axure chrome 浏览器插件的使用
java·chrome
初学小刘2 小时前
机器学习中的聚类与集成算法：从基础到应用
算法·机器学习·聚类
笨蛋不要掉眼泪2 小时前
Spring Boot集成腾讯云人脸识别实现智能小区门禁系统
java·数据库·spring boot
桃源学社(接毕设)2 小时前
云计算下数据隐私保护系统的设计与实现（LW+源码+讲解+部署）
java·云计算·毕业设计·swing·隐私保护
热门推荐
01UV安装并设置国内源02Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code03KGG转MP3工具|非KGM文件|解密音频04DeepSeek更新！速览DeepSeek V3.1新特性05蜘蛛磁力 搜索引擎大全，如何使用蜘蛛磁力查找磁力链接06Claude Code VSCode集成开发指南：AI编程助手完整配置07【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）08Spring 调试终于不再痛苦了092025最新国内服务器可用docker源仓库地址大全（2025年8月更新）10NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南