逻辑回归算法基础介绍，简单的二分类三分类实例

[逻辑回归：从原理到实践，详解这个 "名不副实" 的分类神器](#逻辑回归：从原理到实践，详解这个 "名不副实" 的分类神器)

[一、逻辑回归是什么？为什么叫 "回归" 却做分类？](#一、逻辑回归是什么？为什么叫 "回归" 却做分类？)

二、逻辑回归的核心原理

[2.1 从线性回归到逻辑回归](#2.1 从线性回归到逻辑回归)

[2.2 Sigmoid 函数：概率的 "转换器"](#2.2 Sigmoid 函数：概率的 "转换器")

[2.3 逻辑回归的数学表达](#2.3 逻辑回归的数学表达)

逻辑回归：从原理到实践，详解这个 "名不副实" 的分类神器

逻辑回归（Logistic Regression）是机器学习中最基础也最常用的算法之一。尽管名字中带有 "回归" 二字，但它实际上是一种强大的分类算法，在信贷风控、医疗诊断、用户流失预测等众多领域都有广泛应用。本文将带你从零开始，深入理解逻辑回归的原理、实现与应用。

一、逻辑回归是什么？为什么叫 "回归" 却做分类？

逻辑回归是一种用于解决二分类（0/1）问题的统计学习方法，它通过对数据的建模来预测某个事件发生的概率。比如：

邮件是垃圾邮件（1）还是正常邮件（0）
用户会点击广告（1）还是不会（0）
病人患有某种疾病（1）还是没有（0）

为什么这种分类算法会被称为 "回归"？这是因为逻辑回归本质上是通过回归的方式来计算事件发生的概率，然后根据概率进行分类。它延续了线性回归的思想，但通过一个特殊的函数即sigmoid函数将回归结果映射到 [0,1] 区间，从而实现分类功能。

二、逻辑回归的核心原理

2.1 从线性回归到逻辑回归

线性回归的公式大家都很熟悉：

y = w₀ + w₁x₁ + w₂x₂ + ... + wₙxₙ

其中 y 是连续的输出值。但在分类问题中，我们需要的是离散的类别（如 0 或 1），或者某个事件发生的概率（0 到 1 之间）。

如果直接用线性回归来解决分类问题，会有两个明显的缺陷：

输出值可能超出 [0,1] 范围，无法表示概率
分类问题的决策边界往往不是线性的，线性模型难以拟合

因此，我们需要一个函数来将线性回归的输出转换为概率值，这个函数就是Sigmoid 函数。

2.2 Sigmoid 函数：概率的 "转换器"

Sigmoid 函数的数学表达式如下：

σ(z) = 1 / (1 + e⁻ᶻ)

其中 z 是线性回归的输出（z = w₀ + w₁x₁ + ... + wₙxₙ）

Sigmoid 函数的图像是一条 S 形曲线：

它有几个重要特性：

输出值始终在 (0,1) 区间内，非常适合表示概率
当 z=0 时，σ(z)=0.5
当 z→+∞时，σ(z)→1；当 z→-∞时，σ(z)→0
函数连续可导，便于后续的参数优化

2.3 逻辑回归的数学表达

结合线性回归和 Sigmoid 函数，我们得到逻辑回归的模型表达式：

P(y=1|x) = 1 / (1 + e⁻⁽ʷ⁰⁺ʷ¹ˣ¹⁺...⁺ʷⁿˣⁿ⁾)

P(y=0|x) = 1 - P(y=1|x)

其中 P (y=1|x) 表示在给定特征 x 的条件下，样本属于类别 1 的概率。

有了概率之后，我们需要设定一个阈值（通常是 0.5）来进行分类：

当 P (y=1|x) ≥ 0.5 时，预测为类别 1
当 P (y=1|x) < 0.5 时，预测为类别 0

三.梯度下降：寻找最优参数

我们可以类比"深夜被困深山需下山"的场景，解释梯度下降的基本原理：在受限视野（局部信息）下，通过寻找当前最陡下降方向逐步移动到更低点

梯度方向是函数值增长最快的方向，实际应用中需加负号以转为下降方向。

1.数学原理和计算步骤：

梯度下降需对多变量（如θ₁、θ₂）分别求偏导，联合偏导结果确定下降方向。
初始化：随机赋予参数初始值（如θ₁=0.72，θ₂=0.2），代入数据计算当前梯度。
迭代过程：根据学习率（步长）调整参数，沿梯度反方向更新位置，重复计算直至收敛。

2.局部最优与全局最优：

单次梯度下降可能陷入局部最低点（如山脉中的洼地），解决方案是通过多组随机初始化（"多人并行下山"），最终选择最优结果。

3.梯度下降的通用性

适用于任意复杂函数的最小化问题，包容性强，是人工智能训练的核心方法。
区别于直接求解（如最小二乘法），梯度下降通过迭代逼近最优解，体现"训练"过程。

四.API的参数说明

源码如下：

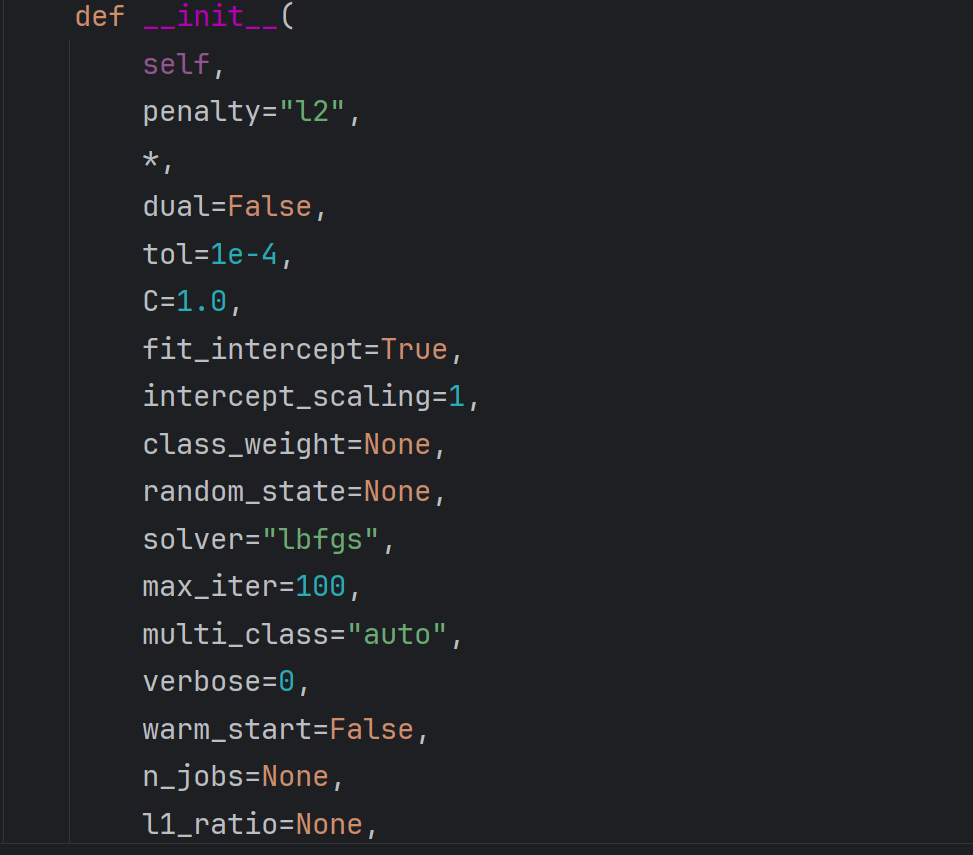
参数说明：

正则化方法：可选L1或L2，与算法选择相关（如牛顿CG）
对偶方法（dual）：仅当正则化选L2时生效，默认值即可。
停止精度（tol）：控制迭代停止条件，当梯度变化极小时终止（避免局部最优或过度计算）。
正则化强度（C）：唯一需调参的参数，默认1.0，需根据模型效果调整。
截距项（fit_intercept）：默认添加（True）。
类别权重（class_weight）：可为不同类别分配权重，默认无。
随机种子（random_state）：固定数据划分结果，确保实验可复现。
最大迭代次数（max_iter）：限制迭代步数（如100次），未收敛则强制停止。
算法选择（solver）：提供多种优化算法（如牛顿法、坐标轴下降法），默认即可。

五.多分类逻辑回归实践

二分类

1.准备数据

datingTestSet2.txt数据内容如下共1000条：

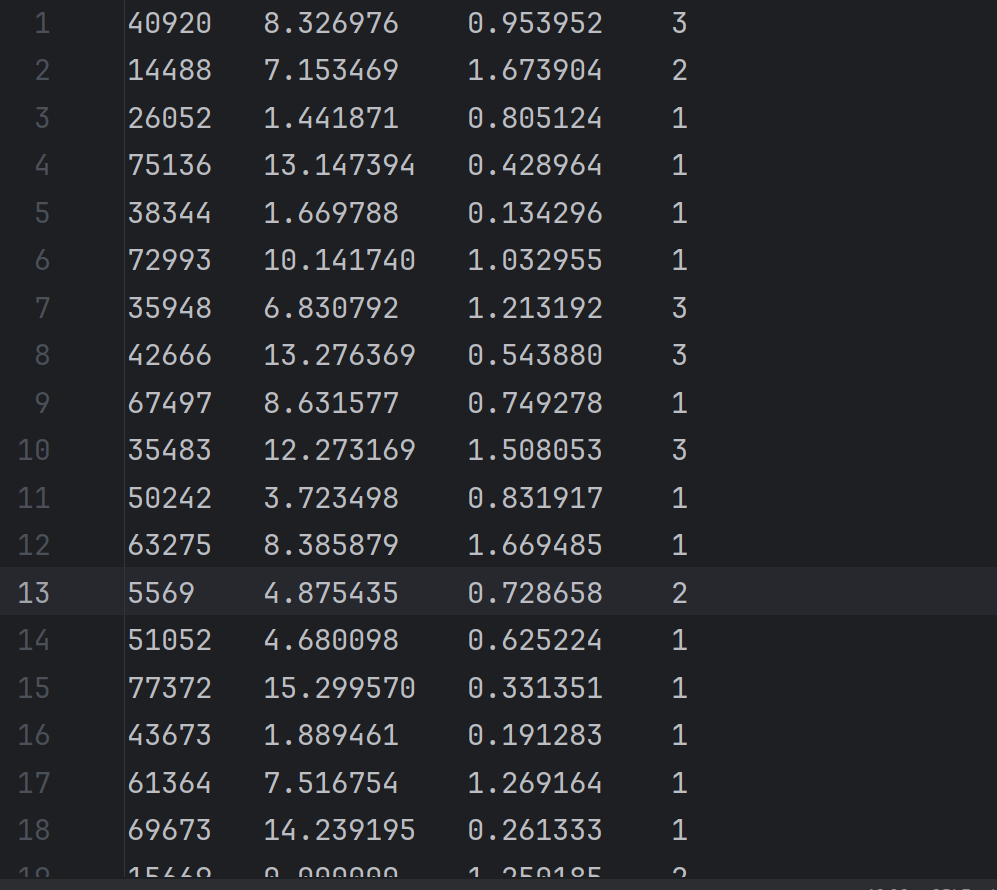
2.导入numpy库读取数据

python 复制代码

import numpy as np
data = np.loadtxt('datingTestSet2.txt')

3.数据处理

由于我们要做的二分类，所以我们要先将txt文件中分类结果为1，2，3的数据单独分开

python 复制代码

data_1 = data[data[:,-1]==1]
data_2 = data[data[:,-1]==2]
data_3 = data[data[:,-1]==3]

然后在用numpy库的concatenate()方法将任意两类结果正确连接起来，这里我们以类别1，2为例

python 复制代码

data_new = np.concatenate((data_1,data_2),axis=0)

最后在对整合后的数据划分特征数据和结果数据

python 复制代码

X=data_new[:,:-1]
y=data_new[:,-1]

4.训练集测试集数据随机划分

数据划分需随机抽取（避免类别偏差），使用train_test_split：
- 参数test_size：指定测试集占比（如0.3）或固定样本数。
- 参数random_state：确保每次划分一致，避免结果波动。

python 复制代码

from sklearn.model_selection import train_test_split
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3,random_state=42)

5.创建模型并训练模型

python 复制代码

from sklearn.linear_model import LogisticRegression
lr=LogisticRegression(C=0.01)
lr.fit(train_x,train_y)

6.预测测试集并计算准确率

python 复制代码

predicted = lr.predict(test_x)
print(predicted)
score = lr.score(test_x,test_y)
print(score)

7.完整代码呈现

python 复制代码

import numpy as np
data = np.loadtxt('datingTestSet2.txt')
data_1 = data[data[:,-1]==1]
data_2 = data[data[:,-1]==2]
data_3 = data[data[:,-1]==3]
data_new = np.concatenate((data_1,data_2),axis=0)
X=data_new[:,:-1]
y=data_new[:,-1]

from sklearn.model_selection import train_test_split
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3,random_state=42)

from sklearn.linear_model import LogisticRegression
lr=LogisticRegression(C=0.01)
lr.fit(train_x,train_y)
predicted = lr.predict(test_x)
print(predicted)
score = lr.score(test_x,test_y)
print(score)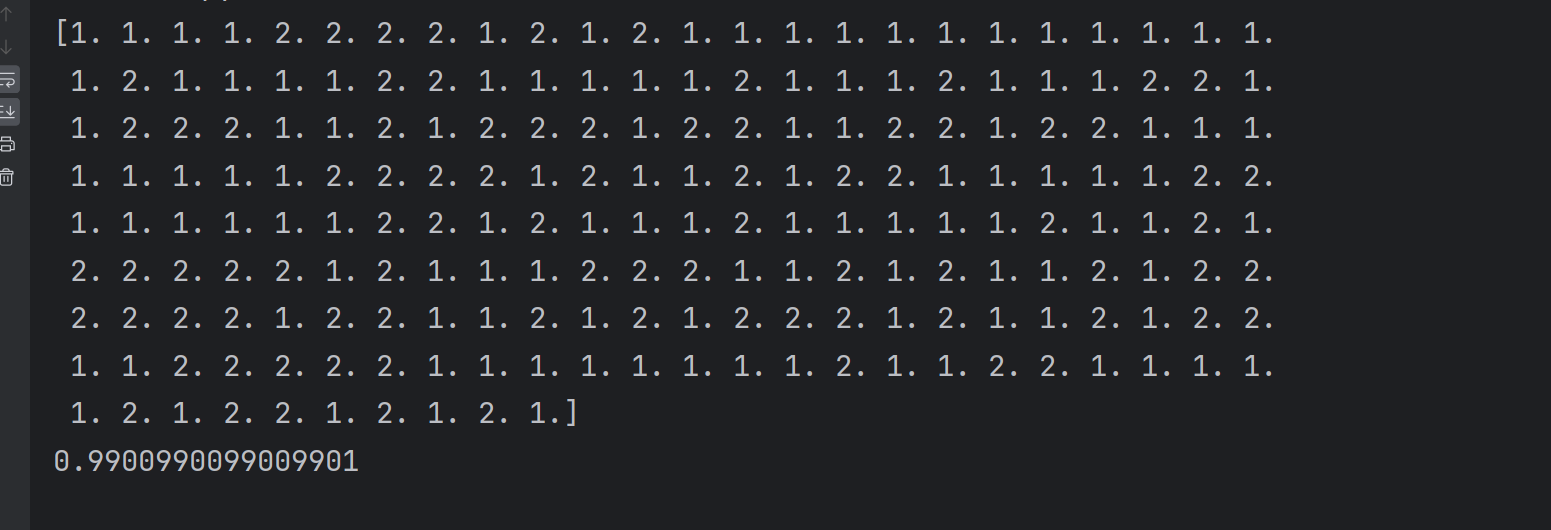

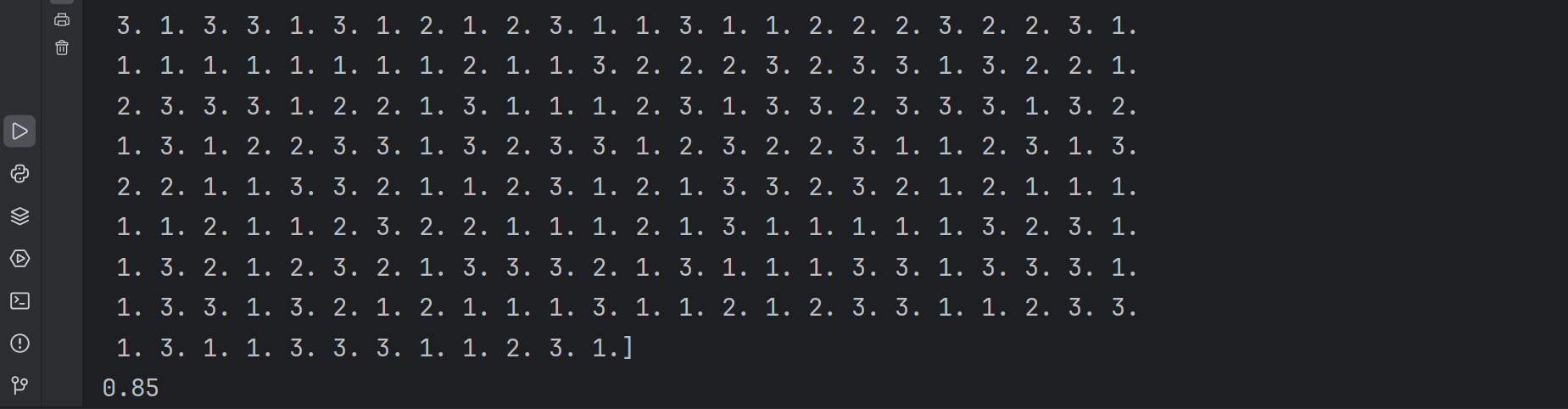
三分类

三分类问题需多条决策线（两两分类），底层仍基于二分类扩展。

在上述二分类的基础上我们只需要数据处理时直接将整个数据划分成特征数据和结果数据，而不需要在根据分类的结果拆分，模型会自己进行三分类训练

完整代码如下：

python 复制代码

import numpy as np
data = np.loadtxt('datingTestSet2.txt')

X=data[:,:-1]
y=data[:,-1]
from sklearn.model_selection import train_test_split
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3,random_state=42)

from sklearn.linear_model import LogisticRegression
lr=LogisticRegression(C=0.01)
lr.fit(train_x,train_y)
predicted = lr.predict(test_x)
print(predicted)
score = lr.score(test_x,test_y)
print(score)