文章目录
- [第二十一课 金融学基础](#第二十一课 金融学基础)
第二十一课 金融学基础
货币的时间价值
货币的时间价值是金融学中最基本的概念。它建立在一个简单的观察之上:今天的一元钱比未来的一元钱更值钱。这种价值差异的核心在于利率的存在。
终值:未来货币量的度量
终值是指在现行利率下,与一个现金流等价的未来货币量。
-
基本逻辑 :给定市场利率为 r,当前的 x 元等价于一年后的
x(1+r)元。例如,当利率为百分之五时,当前的一百元相当于一年后的一百零五元。 -
复利效应:当现金流持续多年时,终值会体现出显著的复利积累。以每年年初投入一元、持续三十年的现金流为例:
- 在利率为百分之五时,三十年后的终值约为七十元。计算过程为:
( 1 + 0.05 ) 30 + ( 1 + 0.05 ) 29 + ⋯ + ( 1 + 0.05 ) ≈ 70 (1+0.05)^{30}+(1+0.05)^{29}+⋯+(1+0.05)≈70 (1+0.05)30+(1+0.05)29+⋯+(1+0.05)≈70
- 在利率为百分之三时,三十年后的终值仅约为四十九元。
-
机会成本视点:利率不仅是存款的回报,更可以被视为持有现金的机会成本。由于持有现金意味着放弃了将其存入市场所能获得的利息,因此利率越高,持有现金的代价就越大。
现值:当前货币量的度量
现值是指在现行利率下,与一个未来现金流等价的当前货币量。将未来的金额转化为当前价值的过程被称为折现。
-
基本逻辑 :如果利率为 r,未来 n 年后的一笔钱 F 的现值为:
P V = F ( 1 + r ) n PV=\frac{F}{(1+r)^n} PV=(1+r)nF -
案例分析:当利率为百分之五时:一年后的一百元,现值只有九十五点二四元。五十后的一百元,现值仅约为八点七二元。这说明时间跨度越长,未来货币的当前价值萎缩得越厉害。
-
连续现金流的加总 :对于多期发生的现金流,其现值是各期金额现值的总和。例如,每年年底支付一元、持续五十年的现金流,其总现值为:
1 1.05 + 1 1.05 2 + . . . + 1 1.05 50 ≈ 18.256 \frac{1}{1.05} + \frac{1}{1.05^2} + ... + \frac{1}{1.05^{50}} ≈ 18.256 1.051+1.0521+...+1.05501≈18.256
利率敏感性与长期波动
现值对利率的变化非常敏感。通过对五十年连续现金流的现值进行对比可见:
-
当利率从百分之三上升到百分之七时,同样的现金流现值会从二十五点七三下降到十三点八。这表明利率越高,未来的收益在今天看来就越不值钱。
-
债券定价应用:一个每年年底付息一元、五十后还本一百元的债券,其现值由两部分组成。即五十期利息的现值加上最后一年本金的现值。在百分之五的利率下,该债券的价值约为:
18.256 + 8.72 ≈ 27 18.256+8.72≈27 18.256+8.72≈27
在现实经济中,由于利率在长期内会发生难以预测的波动,这种波动会直接导致资产现值的剧烈起伏,这也是金融市场风险的重要来源。
现值与决策
在掌握了货币时间价值的计算方法后,可以将其作为工具应用于投资评估、方案选择以及房贷安排等具体的经济决策中。现值分析的核心逻辑在于将不同时点的资金流转化到同一时点,从而进行公平的比较。
投资项目的评估
投资决策的基础是比较初始成本与未来回报的现值。
以一项一亿元的初始投资为例,假设其在十年后能产生两亿元的回报。该项目是否值得投资,取决于市场利率水平:
-
当市场利率为百分之五时 :十年后两亿元回报的现值计算公式为:
P V = 2 ( 1 + 0.05 ) 10 ≈ 1.23 PV = \frac{2}{(1+0.05)^{10}} \approx 1.23 PV=(1+0.05)102≈1.23由于一点二三亿元大于初始投入的一亿元,该投资有利可图。从机会成本的角度看,如果将一亿元存入银行,十年后的金额为:
1 × 1.05 10 ≈ 1.63 1 \times 1.05^{10} \approx 1.63 1×1.0510≈1.63
一点六三亿元小于两亿元,说明投资优于存款。
-
当市场利率为百分之八时 :十年后两亿元回报的现值计算公式为:
P V = 2 ( 1 + 0.08 ) 10 ≈ 0.93 PV = \frac{2}{(1+0.08)^{10}} \approx 0.93 PV=(1+0.08)102≈0.93由于零点九三亿元小于一亿元,该投资不划算。此时存款的机会成本更高,一亿元存款在十年后会变为:
1 × 1.08 10 ≈ 2.16 1 \times 1.08^{10} \approx 2.16 1×1.0810≈2.16
-
内部收益率分析 :该项目的年化回报率满足以下等式:
( 1 + r ) 10 = 2 (1+r)^{10} = 2 (1+r)10=2
计算得出 :
r ≈ 7.2 % r \approx 7.2\% r≈7.2%这意味着只有当市场利率低于百分之七点二时,该投资项目才具有吸引力。
不同现金流方案的比较
在面对多种收款或还款方案时,现值工具能帮助辨别哪种方式对决策者更优。以彩票奖金领取方案为例,假设有两种选择:一是五十年内每年年底领取一万元;二是现在一次性领取二十万元。
-
如果市场利率为百分之五 :方案一的现值计算公式为:
P V = ∑ t = 1 50 1 ( 1 + 0.05 ) t ≈ 18.256 PV = \sum_{t=1}^{50} \frac{1}{(1+0.05)^t} \approx 18.256 PV=t=1∑50(1+0.05)t1≈18.256此时十八点二五六万元小于二十万元,选择方案二(一次性领取)更有利。
-
如果市场利率为百分之四 :方案一的现值计算公式为:
P V = ∑ t = 1 50 1 ( 1 + 0.04 ) t ≈ 21.48 PV = \sum_{t=1}^{50} \frac{1}{(1+0.04)^t} \approx 21.48 PV=t=1∑50(1+0.04)t1≈21.48此时二十一点四八万元大于二十万元,选择方案一(分期领取)更有利。
-
决策规律:两个方案在利率约为百分之四点七时等价。利率越高,早领取资金的现值优势就越明显。
房贷还款安排的经济学解析
房贷主要分为等额本息和等额本金两种还款方式。虽然各期金额分布不同,但在现值理论下,它们对银行和借款人是逻辑对等的。
-
等额本息 :每期还款金额完全相等。假设贷款总额为 T,利率为 r,分两期归还,每期还款额为 x。根据现值等式,x 需满足:
x × ( 1 1 + r + 1 ( 1 + r ) 2 ) = T x \times (\frac{1}{1+r} + \frac{1}{(1+r)^2}) = T x×(1+r1+(1+r)21)=T -
等额本金:每期归还的本金相等,利息则根据剩余本金余额计算。假设贷款总额为 T,利率为 r,分两期归还:
- 第一期末还款额为 :
1 2 T + T r \frac{1}{2}T + Tr 21T+Tr
第二期末还款额为 :
1 2 T + 1 2 T r \frac{1}{2}T + \frac{1}{2}Tr 21T+21Tr
- 第一期末还款额为 :
-
核心结论:在相同的市场利率下,无论选择哪种还款方式,所有还款现金流的现值之和均等于贷款总额 T。对于个人而言,如果贷款利率高于其能获得的投资回报率,尽早还款(如选择等额本金或提前还本)在经济上更为有利。
风险态度与效用理论
在金融决策中,不仅要考虑货币的绝对数量,更要考虑个体对风险的心理感受。经济学家引入效用这一概念来衡量个体从财富中获得的满足程度,并以此构建了分析风险态度的标准框架。
效用函数与边际效用递减
效用是心理上的主观评价。对于大多数人来说,随着财富的增加,每一单位新增财富带来的满足感(即边际效用)是不断减少的。这种心理特征决定了人们对风险的基本态度。
在财富效用图中,如果效用曲线是向外凸出的(凹函数),则意味着该个体具有边际效用递减的特征。
三种典型的风险态度
根据个体效用函数的形状,我们可以将其风险态度分为三类:
-
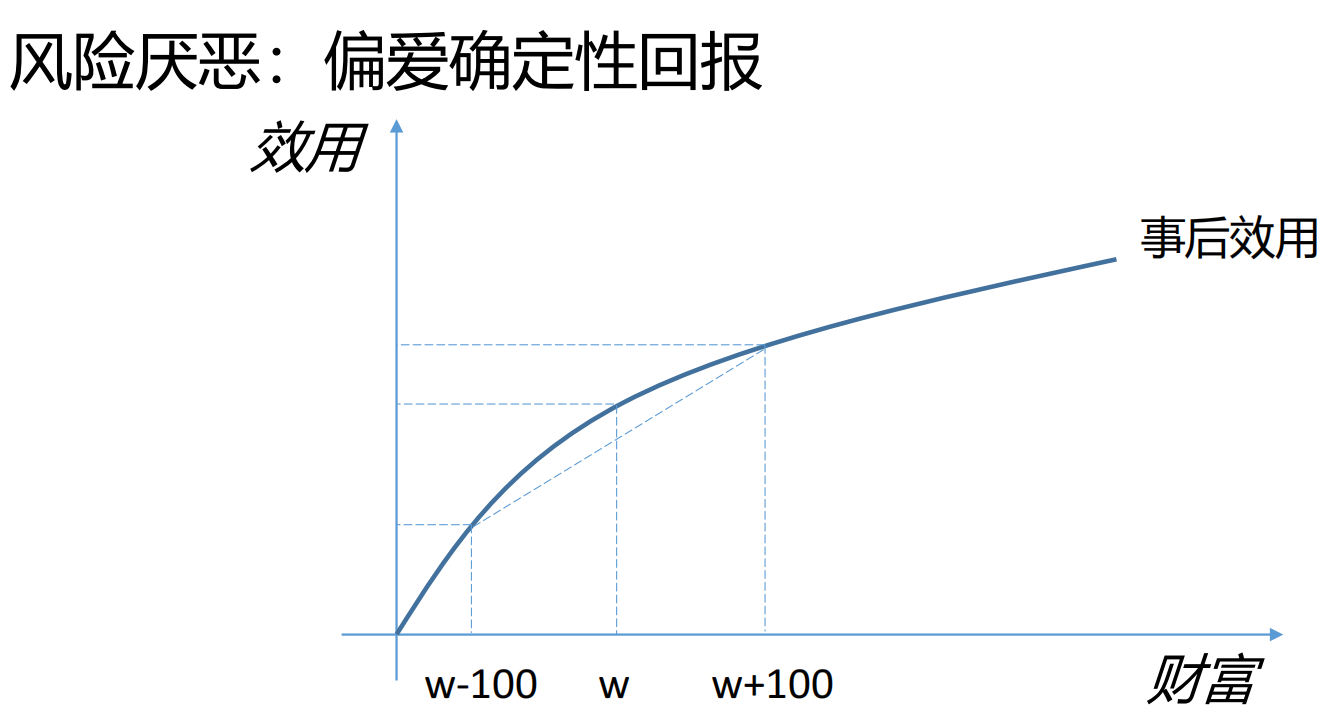
风险厌恶:这是最常见的心理状态。风险厌恶者偏爱确定的回报,而非具有相同期望货币值的赌局。其效用曲线表现为边际效用递减。对于他们而言,失去一百元带来的痛苦要大于得到一百元带来的快乐。
-
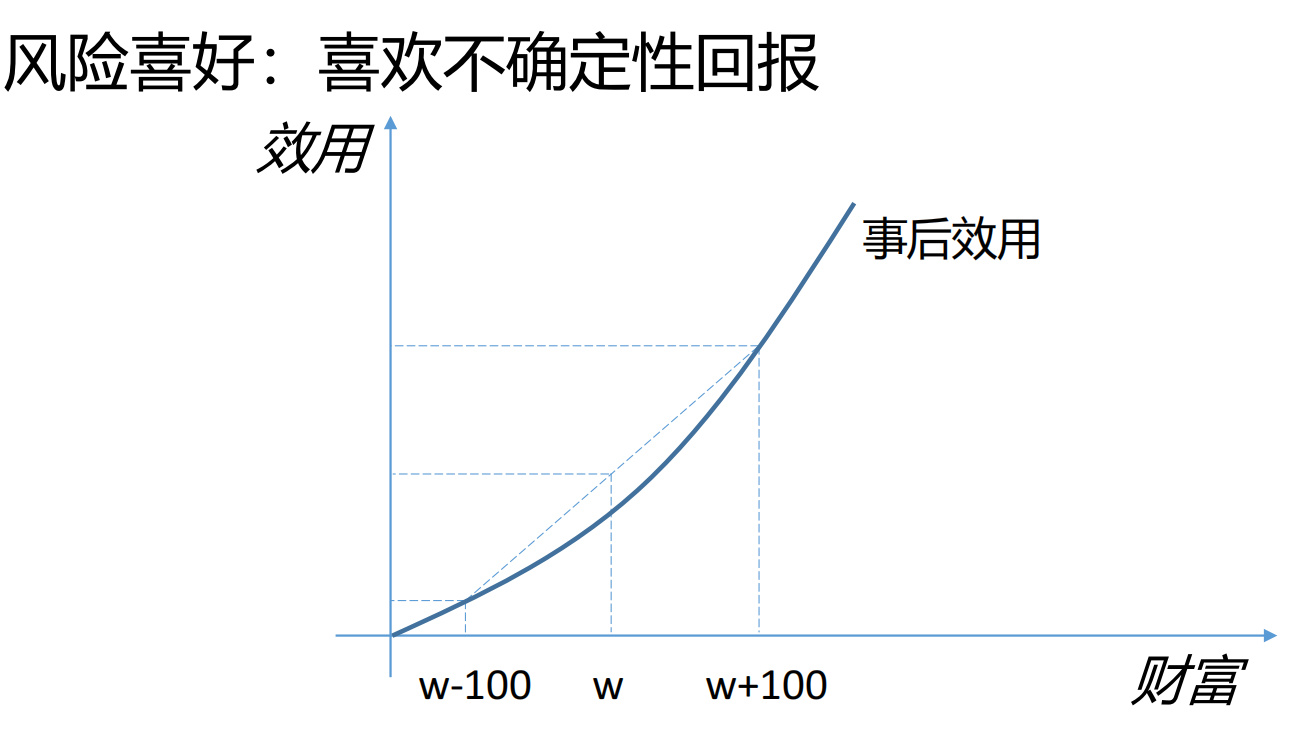
风险喜好 :这类个体喜欢挑战不确定性。其效用曲线表现为边际效用递增(凸函数)。他们认为获得超额回报的可能性带来的效用极大,足以抵消潜在的损失风险。
-
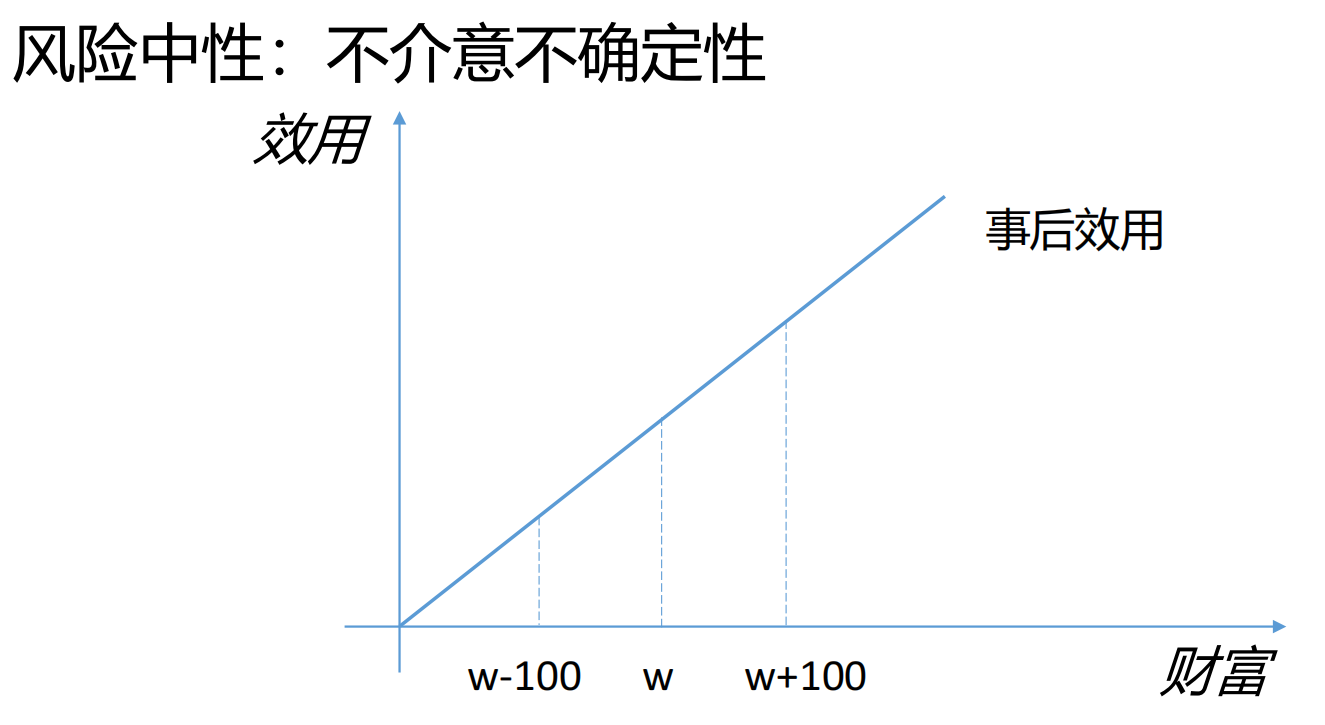
风险中性 :这类个体不介意不确定性,只关注期望的货币回报。其效用函数是一条直线,这意味着财富每增加一元,带来的效用增加量是恒定的。
期望效用理论的计算逻辑
在面临不确定的选择时,理性的决策者并不是最大化期望货币收入,而是最大化期望效用。可以通过一个算例来理解:
假设一个人的效用函数为:
U ( w ) = w U(w) = \sqrt{w} U(w)=w
其初始财富为一百元,此时的初始效用为:
U ( 100 ) = 100 = 10 U(100) = \sqrt{100} = 10 U(100)=100 =10
现在有一个赌局:有百分之五十的概率赢取三百元(总财富变为四百元),有百分之五十的概率维持原状(总财富为一百元)。该赌局的期望货币回报为:
0.5 × 100 + 0.5 × 400 = 250 0.5 \times 100 + 0.5 \times 400 = 250 0.5×100+0.5×400=250
如果参与赌局,该个体的期望效用为:
E [ U ] = 0.5 × 100 + 0.5 × 400 = 0.5 × 10 + 0.5 × 20 = 15 E[U] = 0.5 \times \sqrt{100} + 0.5 \times \sqrt{400} = 0.5 \times 10 + 0.5 \times 20 = 15 E[U]=0.5×100 +0.5×400 =0.5×10+0.5×20=15
如果直接获得两百五十元现金(即赌局的期望货币值),其效用为:
U ( 250 ) = 250 ≈ 15.8 U(250) = \sqrt{250} \approx 15.8 U(250)=250 ≈15.8
由于确定的效用大于赌局的期望效用,一个风险厌恶的人会拒绝参加这个期望回报相等的赌局,转而选择固定的现金。
风险态度的市场体现
个体的风险偏好直接决定了金融市场的运行和产品的设计:
- 保险市场的存在:由于人们普遍存在风险厌恶心理,因此愿意支付一笔确定的费用(保费)来转嫁潜在的巨额损失风险。医疗、财产、人身和养老保险均基于此逻辑。
- 投资多元化:风险厌恶者通过在不同资产间分散投资,利用风险抵消的原理,在不降低期望收益的前提下降低整体风险。
- 资产定价:风险越高的资产,通常需要提供更高的期望收益率,才能吸引风险厌恶的投资者。
- 风险喜好的行业:赌博、彩票以及近年来流行的盲盒,其受众群体往往在这些特定领域表现出风险喜好的特征。
资产定价与市场效率
资产定价不仅是金融计算的结果,更是市场参与者信息博弈与心理反应的体现。本模块讨论如何评估资产价值,以及市场在多大程度上能够反映这些价值。
资产价值评估的主要流派
在金融市场上,判断一项资产(如股票)是否被高估或低估,主要有两种视角:
- 基本面分析:这种方法主张通过深入研究企业或资产的盈利前景、管理水平、行业竞争地位等因素来估算其内在价值。如果市场价格低于估算的内在价值,则该资产具有投资价值。
- 有效市场假说:这一理论认为,资产的交易价格已经充分反映了与该资产价值有关的所有公开信息。在有效的市场中,寻找被低估的股票几乎是不可能的,因为价格会迅速调整以匹配新信息。
有效市场假说的三种程度
根据市场反映信息的效率和范围,有效市场通常被划分为三个层次:
- 弱有效市场:以往的价格信息已完全反映在当前价格中。这意味着基于历史走势的"技术分析"是无法获得超额收益的。
- 弱强有效市场:所有公开可获得的信息(如财务报表、新闻公告)都已完全反映在当前价格中。
- 强有效市场:即便掌握了内幕信息的投资者也无法获取超额收益,因为价格已经反映了包括未公开信息在内的所有信息。
- 现实案例:消极管理基金(如指数基金)与主动管理基金的业绩表现对比。如果市场是高度有效的,那么收费低廉、被动跟踪市场的指数基金往往能跑赢大多数试图通过精选股票获利的主动管理基金。
非理性市场与行为金融学
尽管有效市场假说提供了完美的理论框架,但现实中的资产价格经常出现短期大幅波动,这引出了非理性市场的讨论:
- 市场异象:由于投资者的心理偏差,市场经常出现资产泡沫、羊群效应(盲目跟风)等现象。
- 认知局限:信息不对称和人类认知能力的限制,使得价格有时会偏离理性预期。
展望理论与心理价值
作为行为金融学的基石,展望理论揭示了人在面临风险决策时,心理价值与客观损益之间的非线性关系。
-
价值函数的核心特征:人们在面对得利和损失时,心理感受是不对称的。这体现在价值函数曲线的形状上。
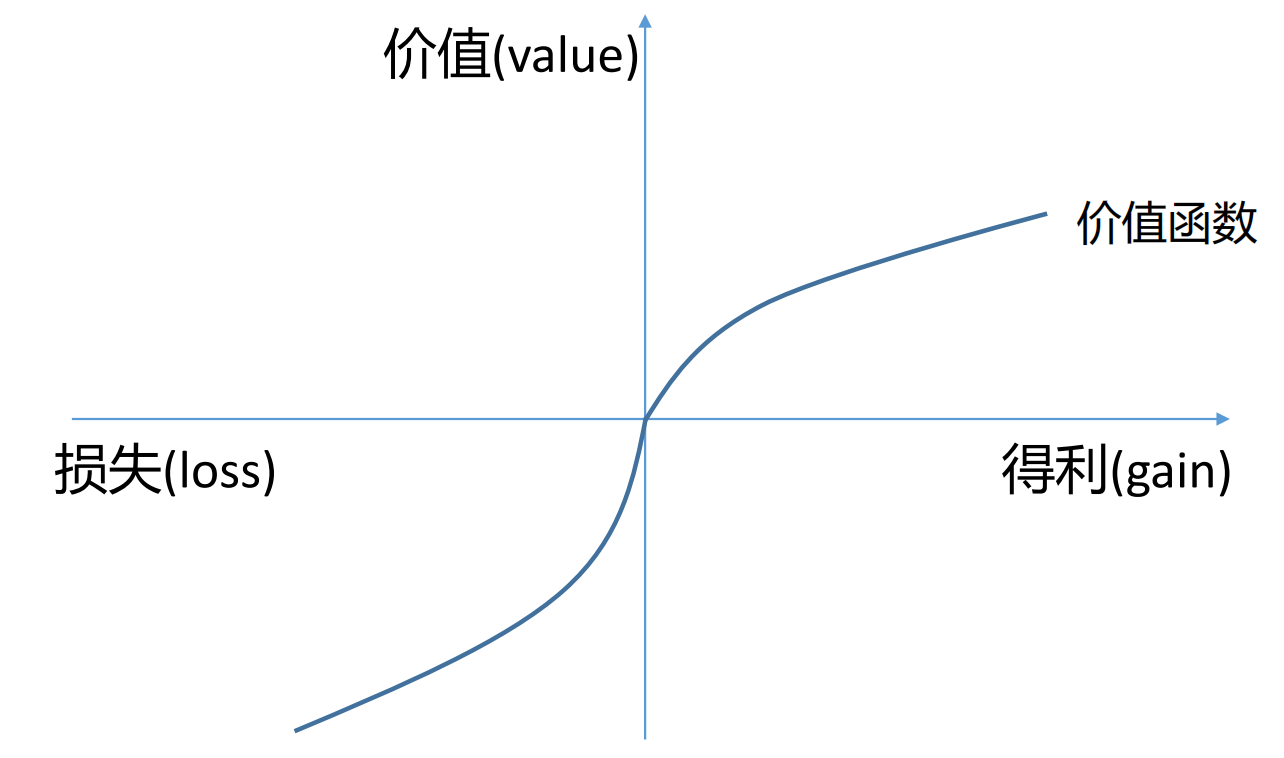
V ( x ) 在 x > 0 时是凹的(收益递减),在 x < 0 时是凸的(损失敏感)。 V(x) \text{ 在 } x > 0 \text{ 时是凹的(收益递减),在 } x < 0 \text{ 时是凸的(损失敏感)。} V(x) 在 x>0 时是凹的(收益递减),在 x<0 时是凸的(损失敏感)。
-
损失厌恶:在价值函数图中,损失区域的曲线通常比得利区域的曲线更陡峭。这意味着相同数额的损失带来的痛苦,远大于相同数额的得利带来的快乐。这种心理倾向会导致投资者在亏损时过度冒险以求回本,而在盈利时则过于保守。