世代距离（GD）和反转世代距离（IGD）详析

行然梦实2025-08-02 13:13

前言

提醒：

文章内容为方便作者自己后日复习与查阅而进行的书写与发布，其中引用内容都会使用链接表明出处（如有侵权问题，请及时联系）。

其中内容多为一次书写，缺少检查与订正，如有问题或其他拓展及意见建议，欢迎评论区讨论交流。
内容由AI辅助生成，仅经笔者审核整理，请甄别食用。

文章目录

  • 前言
      • [一、世代距离（GD）------ 聚焦收敛性的度量](#一、世代距离（GD）—— 聚焦收敛性的度量)
        • [1. 核心目标](#1. 核心目标)
        • [2. 数学公式与拆解](#2. 数学公式与拆解)
        • [3. 物理意义](#3. 物理意义)
        • [4. 可视化示例](#4. 可视化示例)
      • [二、反转世代距离（IGD）------ 收敛+多样性双维度度量](#二、反转世代距离（IGD）—— 收敛+多样性双维度度量)
        • [1. 核心目标](#1. 核心目标)
        • [2. 数学公式与拆解](#2. 数学公式与拆解)
        • [3. 物理意义](#3. 物理意义)
        • [4. 可视化示例](#4. 可视化示例)
      • [三、GD vs IGD ------ 核心差异与适用场景](#三、GD vs IGD —— 核心差异与适用场景)
      • 五、总结

一、世代距离（GD）------ 聚焦收敛性的度量

1. 核心目标

衡量近似解集 A A A到真实帕累托前沿 P F PF PF的"收敛差距"，即算法生成的解是否足够接近最优前沿。

2. 数学公式与拆解

G D = 1 ∣ A ∣ ( ∑ i = 1 ∣ A ∣ dis ( a i , P F ′ ) p ) 1 p GD = \frac{1}{|A|} \left( \sum_{i=1}^{|A|} \text{dis}(a_i, PF')^p \right)^{\frac{1}{p}} GD=∣A∣1 i=1∑∣A∣dis(ai,PF′)p p1

  • 符号定义 ：
    • ∣ A ∣ |A| ∣A∣：近似解集 A A A的规模（解的数量，如算法最终保留的非支配解个数）；
    • P F ′ PF' PF′：真实帕累托前沿 P F PF PF的简化子集 （因 P F PF PF可能连续，需采样离散点集，保证计算可行性）；
    • dis ( a i , P F ′ ) \text{dis}(a_i, PF') dis(ai,PF′)：近似解 a i a_i ai到 P F ′ PF' PF′的最小欧氏距离 ，即 a i a_i ai与 P F ′ PF' PF′中所有点的距离最小值，公式为：
      dis ( a i , P F ′ ) = min ⁡ p ∈ P F ′ ∑ m = 1 M ( a i , m − p m ) 2 \text{dis}(a_i, PF') = \min_{p \in PF'} \sqrt{\sum_{m=1}^M (a_{i,m} - p_m)^2} dis(ai,PF′)=p∈PF′minm=1∑M(ai,m−pm)2
      （ M M M是目标维度， a i , m a_{i,m} ai,m是 a i a_i ai的第 m m m个目标值， p m p_m pm是 P F ′ PF' PF′中点 p p p的第 m m m个目标值）；
    • p p p：范数参数 ，通常取 p = 2 p=2 p=2（计算均方根距离，突出离群点；取 p = 1 p=1 p=1则为平均距离）。
3. 物理意义
  • 收敛性 ： G D GD GD越小，说明近似解整体越贴近真实帕累托前沿，算法的收敛性越好；
  • 局限性 ：仅关注"解是否够好"，不衡量"解是否覆盖前沿"（比如所有解扎堆在前沿某区域， G D GD GD也可能很小，但多样性差）。
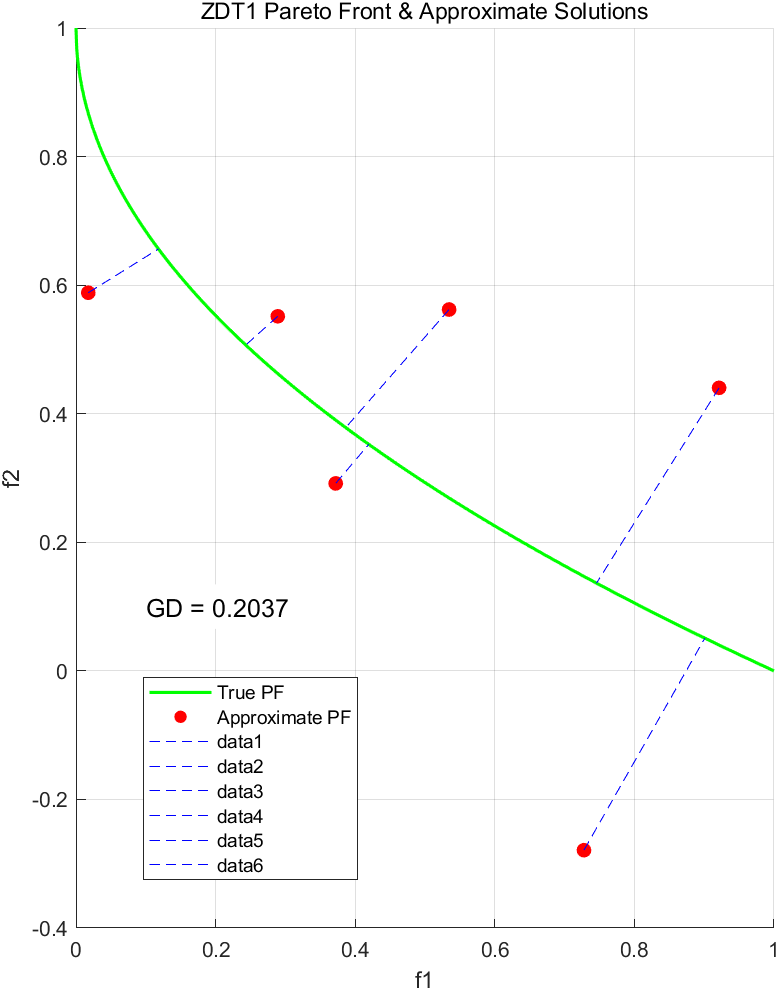
4. 可视化示例

二维可视化代码以及运行结果：

matlab 复制代码 
clc; clear; close all;

%% 设置参数
N_true = 1000;   % 真实帕累托前沿点数（少量）
N_approx = 6;  % 近似前沿点数（更少）

%% 生成 ZDT1 的真实帕累托前沿
x_true = linspace(0,1,N_true)';
f1_true = x_true;
f2_true = 1 - sqrt(x_true);
true_pf = [f1_true, f2_true];

%% 模拟近似帕累托前沿（稍微偏离真实解）
rng(1);
x_approx = linspace(0.05, 0.95, N_approx)' + 0.05*randn(N_approx,1);
x_approx = min(max(x_approx,0),1);
f1_approx = x_approx;
f2_approx = 1 - sqrt(x_approx) + 0.5*randn(N_approx,1);
approx_pf = [f1_approx, f2_approx];

%% 可视化解集
figure; hold on; grid on;
plot(f1_true, f2_true, 'g-', 'LineWidth', 1.5);
scatter(f1_approx, f2_approx, 50, 'r', 'filled');
legend('True PF', 'Approximate PF', 'Location','best');
xlabel('f1'); ylabel('f2');
title('ZDT1 Pareto Front & Approximate Solutions');

%% 可视化计算过程 + GD
distances = zeros(N_approx, 1);
for i = 1:N_approx
    % 当前近似点
    p = approx_pf(i, :);
    % 到所有真实点的欧式距离
    d = vecnorm(true_pf - p, 2, 2);
    [min_dist, idx] = min(d);
    distances(i) = min_dist;
    
    % 可视化该点与最近真实点之间的距离线
    q = true_pf(idx, :);
    plot([p(1), q(1)], [p(2), q(2)], 'b--'); % 蓝色虚线表示距离
end

% 计算 GD
GD = mean(distances);
text(0.1, 0.1, ['GD = ', num2str(GD, '%.4f')], 'FontSize', 12, 'BackgroundColor', 'w');

运行结果

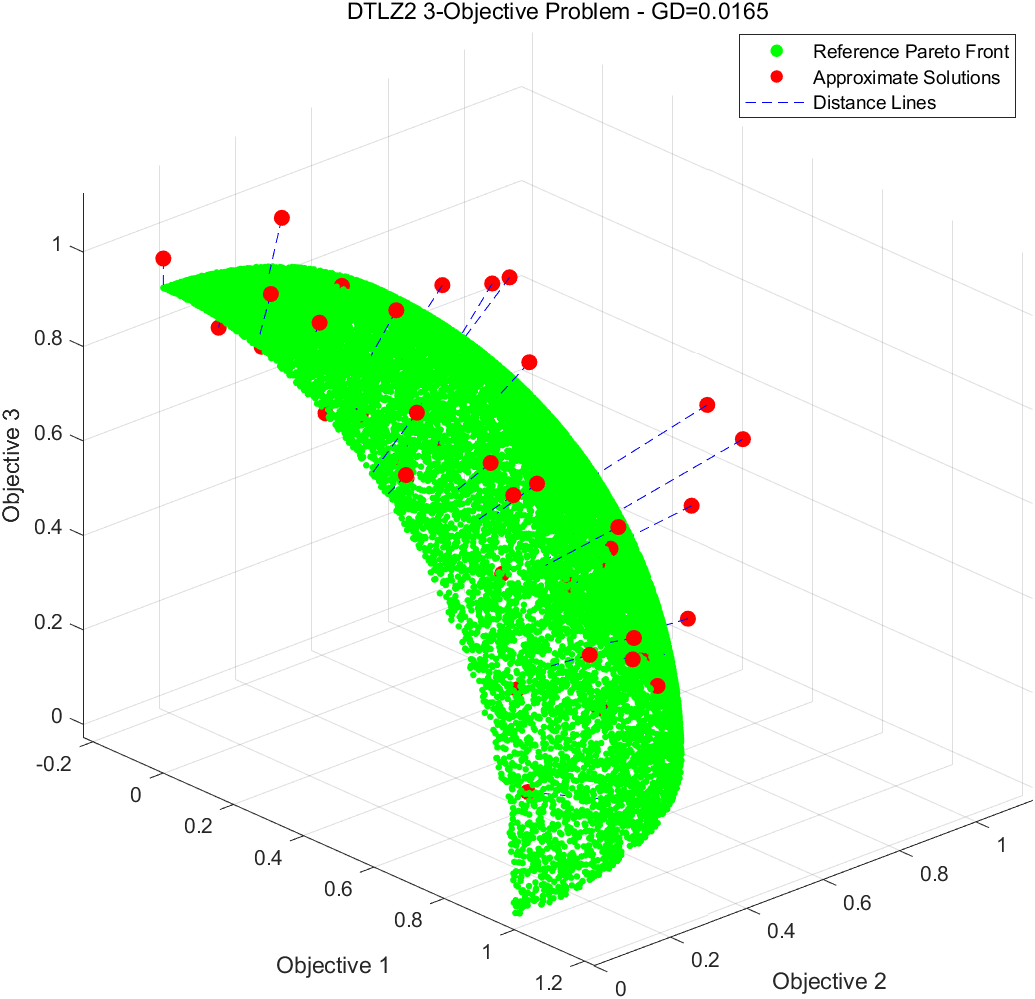
三维可视化代码以及运行结果：

matlab 复制代码 
clc; clear; close all;

%% 参数设置
M = 3;                  % 目标数（三维）
refPointsNum = 20000;    % 参考前沿点数量（大量）
approxPointsNum = 50;   % 近似解数量（较少）
disturbance = 0.1;     % 扰动大小（控制近似解与参考点距离）

%% 生成参考帕累托前沿（单位球面均匀分布点）
theta1 = rand(refPointsNum,1)*pi/2;
theta2 = rand(refPointsNum,1)*pi/2;

f1 = cos(theta1).*cos(theta2);
f2 = cos(theta1).*sin(theta2);
f3 = sin(theta1);
RefFront = [f1 f2 f3];
RefFront = RefFront ./ vecnorm(RefFront,2,2);

%% 生成少量近似解，扰动控制在disturbance范围内
idxSample = randsample(refPointsNum, approxPointsNum);
PopObjs = RefFront(idxSample,:) + disturbance*randn(approxPointsNum, M);
PopObjs = max(PopObjs, 0);          % 保持非负
% PopObjs = PopObjs ./ vecnorm(PopObjs,2,2); % 归一化，保证落在球面附近
PopObjs = PopObjs;
%% 计算世代距离（GD）
distances = zeros(approxPointsNum,1);
for i = 1:approxPointsNum
    d = sqrt(sum((RefFront - PopObjs(i,:)).^2, 2));
    distances(i) = min(d);
end
GD = sqrt(sum(distances.^2))/approxPointsNum;

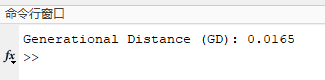
fprintf('Generational Distance (GD): %.4f\n', GD);

%% 可视化
figure; hold on; grid on; axis equal;
scatter3(RefFront(:,1), RefFront(:,2), RefFront(:,3), 10, 'g', 'filled');
scatter3(PopObjs(:,1), PopObjs(:,2), PopObjs(:,3), 60, 'r', 'filled');

% 画距离连线
for i = 1:approxPointsNum
    d = sqrt(sum((RefFront - PopObjs(i,:)).^2, 2));
    [~, idx] = min(d);
    plot3([PopObjs(i,1) RefFront(idx,1)], ...
          [PopObjs(i,2) RefFront(idx,2)], ...
          [PopObjs(i,3) RefFront(idx,3)], 'b--');
end

xlabel('Objective 1'); ylabel('Objective 2'); zlabel('Objective 3');
title(sprintf('DTLZ2 3-Objective Problem - GD=%.4f', GD));
legend('Reference Pareto Front','Approximate Solutions','Distance Lines');
view(45,30);

运行结果

二、反转世代距离（IGD）------ 收敛+多样性双维度度量

1. 核心目标

同时衡量近似解集 A A A的收敛性（贴近 P F PF PF）和多样性（覆盖 P F PF PF），即解是否"又好又全"。

2. 数学公式与拆解

I G D = 1 ∣ P F ′ ∣ ( ∑ i = 1 ∣ P F ′ ∣ dis ( p i , A ) p ) 1 p IGD = \frac{1}{|PF'|} \left( \sum_{i=1}^{|PF'|} \text{dis}(p_i, A)^p \right)^{\frac{1}{p}} IGD=∣PF′∣1 i=1∑∣PF′∣dis(pi,A)p p1

  • 符号定义 ：
    • ∣ P F ′ ∣ |PF'| ∣PF′∣：真实帕累托前沿子集 P F ′ PF' PF′的规模（采样点数量，需均匀覆盖 P F PF PF）；
    • dis ( p i , A ) \text{dis}(p_i, A) dis(pi,A)： P F ′ PF' PF′中的点 p i p_i pi到近似解集 A A A的最小欧氏距离 （即 p i p_i pi与 A A A中最近点的距离），公式为：
      dis ( p i , A ) = min ⁡ a ∈ A ∑ m = 1 M ( p i , m − a m ) 2 \text{dis}(p_i, A) = \min_{a \in A} \sqrt{\sum_{m=1}^M (p_{i,m} - a_m)^2} dis(pi,A)=a∈Aminm=1∑M(pi,m−am)2
      （ p i , m p_{i,m} pi,m是 p i p_i pi的第 m m m个目标值， a m a_m am是 A A A中点 a a a的第 m m m个目标值）；
    • p p p：同 GD，通常取 p = 2 p=2 p=2。
3. 物理意义
  • 收敛性 ： I G D IGD IGD越小，说明 P F ′ PF' PF′到 A A A的距离越小， A A A越贴近 P F PF PF；
  • 多样性 ：若 A A A分布稀疏（比如只覆盖 P F PF PF的局部区域），则 P F ′ PF' PF′中远离 A A A的点会使 I G D IGD IGD增大，因此 I G D IGD IGD能惩罚"解分布不均"的问题；
  • 优势：相比 GD，IGD 更全面，能同时反映"解的质量"和"解的覆盖性"。
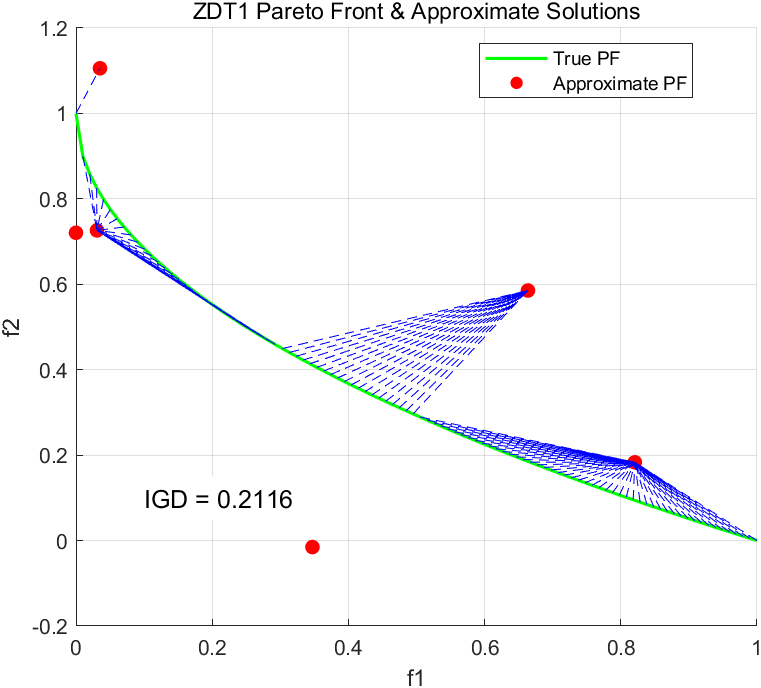
4. 可视化示例

二维可视化代码以及运行结果：

matlab 复制代码 
clc; 
clear; 
close all;

%% 设置参数
N_true = 100;   % 真实帕累托前沿点数
N_approx = 6;    % 近似前沿点数
perturbation_size = 0.5;  % 扰动大小

%% 生成 ZDT1 的真实帕累托前沿
x_true = linspace(0, 1, N_true)';
f1_true = x_true;
f2_true = 1 - sqrt(x_true);
true_pf = [f1_true, f2_true];

%% 模拟近似帕累托前沿（稍微偏离真实解）
rng(1);
x_approx = linspace(0.05, 0.95, N_approx)' + perturbation_size * randn(N_approx, 1);
x_approx = min(max(x_approx, 0), 1);  % 限制在 [0, 1] 范围内
f1_approx = x_approx;
f2_approx = 1 - sqrt(x_approx) + perturbation_size * randn(N_approx, 1);
approx_pf = [f1_approx, f2_approx];

%% 可视化解集
figure; hold on; grid on;
plot(f1_true, f2_true, 'g-', 'LineWidth', 1.5, 'DisplayName', 'True PF');  % 绘制真实帕累托前沿
scatter(f1_approx, f2_approx, 50, 'r', 'filled', 'DisplayName', 'Approximate PF');  % 绘制近似前沿
xlabel('f1'); ylabel('f2');
title('ZDT1 Pareto Front & Approximate Solutions');

%% 计算 IGD
distances = zeros(N_true, 1);  % 存储每个真实点到最近近似点的距离
for i = 1:N_true
    % 当前真实点
    p = true_pf(i, :);
    % 到所有近似点的欧式距离
    d = vecnorm(approx_pf - p, 2, 2);
    % 记录最近的距离
    distances(i) = min(d);
end

% 计算 IGD
IGD = mean(distances);
% 可视化计算过程
for i = 1:N_true
    % 当前真实点
    p = true_pf(i, :);
    % 到所有近似点的欧式距离
    d = vecnorm(approx_pf - p, 2, 2);
    [min_dist, idx] = min(d);  % 找到最近的近似点

    % 可视化该真实点与最近近似点之间的距离线
    q = approx_pf(idx, :);
    plot([p(1), q(1)], [p(2), q(2)], 'b--'); % 蓝色虚线表示距离
end

% 显示 IGD
text(0.1, 0.1, ['IGD = ', num2str(IGD, '%.4f')], 'FontSize', 12, 'BackgroundColor', 'w');

% 添加图例，显示'非数据'标签
legend('True PF', 'Approximate PF', 'Location', 'best');
hold off;

运行结果

三维可视化代码以及运行结果：

matlab 复制代码 
clc; clear; close all;

%% 参数配置
M = 3;                  % 目标函数维度（三维）
refPointsNum = 50;     % 参考帕累托前沿点数量
approxPointsNum = 8;   % 近似解数量
disturbance = 0.08;     % 扰动大小（控制近似解质量）

%% 生成DTLZ2参考帕累托前沿（PF）
theta1 = linspace(0, pi/2, sqrt(refPointsNum))';
theta2 = linspace(0, pi/2, sqrt(refPointsNum));
[Theta1, Theta2] = meshgrid(theta1, theta2);

% 计算目标函数值
f1 = cos(Theta1) .* cos(Theta2);
f2 = cos(Theta1) .* sin(Theta2);
f3 = sin(Theta1);

% 转换为向量形式并归一化
PF = [f1(:) f2(:) f3(:)];
PF = PF ./ vecnorm(PF, 2, 2);  % 单位球面归一化

%% 生成近似解（A）
idxSample = randsample(size(PF, 1), approxPointsNum);
A = PF(idxSample, :) + disturbance * randn(approxPointsNum, M);
A = max(min(A, 1), 0);  % 限制在合理范围

%% 计算反转世代距离（IGD）
% IGD公式：IGD = (1/|PF|) * Σ(min距离(PF_i, A)) 
% 物理意义：每个参考点到最近近似解的平均距离（PF→A）
igd_distances = zeros(size(PF, 1), 1);
for i = 1:size(PF, 1)
    % 计算PF中每个点到所有近似解的距离
    dists = sqrt(sum((A - PF(i, :)).^2, 2));
    igd_distances(i) = min(dists);  % 取最近距离
end
IGD = mean(igd_distances);

%% 计算世代距离（GD）
% GD公式：GD = (1/|A|) * Σ(min距离(A_j, PF))
% 物理意义：每个近似解到最近参考点的平均距离（A→PF）
gd_distances = zeros(size(A, 1), 1);
for j = 1:size(A, 1)
    % 计算每个近似解到所有PF点的距离
    dists = sqrt(sum((PF - A(j, :)).^2, 2));
    gd_distances(j) = min(dists);  % 取最近距离
end
GD = mean(gd_distances);

%% 输出结果
fprintf('反转世代距离 (IGD)：%.4f\n', IGD);
fprintf('世代距离 (GD)：%.4f\n', GD);

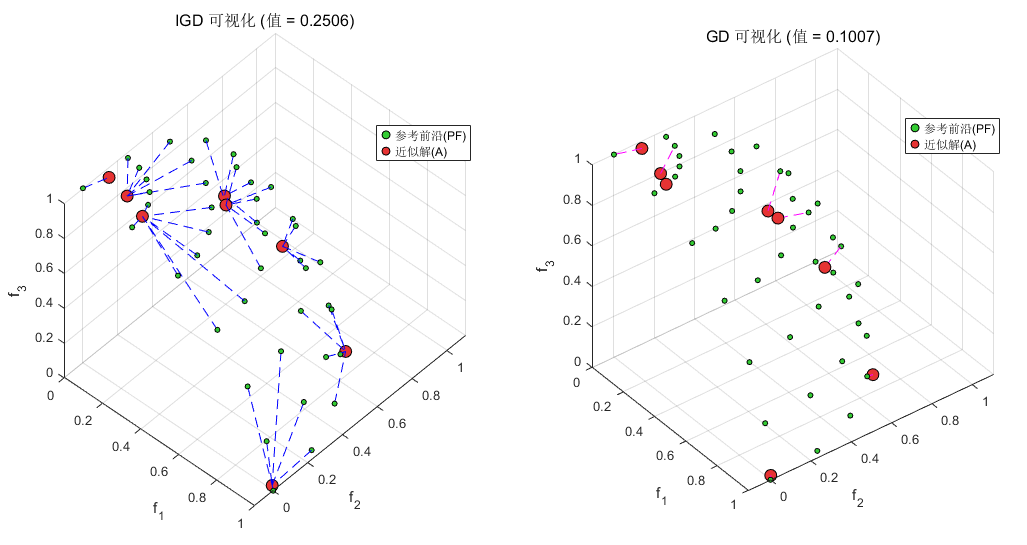
%% 可视化对比
figure('Position', [100, 100, 1200, 600], 'Color', 'w');

% 左侧：IGD可视化（PF→A的距离）
subplot(1, 2, 1); hold on; grid on; axis equal;
scatter3(PF(:, 1), PF(:, 2), PF(:, 3), 15, [0.2 0.8 0.2], ...
         'filled', 'MarkerEdgeColor', 'k', 'DisplayName', '参考前沿(PF)');
scatter3(A(:, 1), A(:, 2), A(:, 3), 80, [0.9 0.2 0.2], ...
         'filled', 'MarkerEdgeColor', 'k', 'DisplayName', '近似解(A)');

% 绘制IGD距离线（PF到A的最近距离）
for i = 1:min(50, size(PF, 1))  % 采样部分点绘制，避免图过乱
    dists = sqrt(sum((A - PF(i, :)).^2, 2));
    [~, nearestIdx] = min(dists);
    plot3([PF(i, 1), A(nearestIdx, 1)], ...
          [PF(i, 2), A(nearestIdx, 2)], ...
          [PF(i, 3), A(nearestIdx, 3)], ...
          'b--', 'LineWidth', 0.5, 'HandleVisibility', 'off');
end
title(sprintf('IGD 可视化 (值 = %.4f)', IGD), 'FontSize', 12);
xlabel('f_1'); ylabel('f_2'); zlabel('f_3');
legend('Location', 'best');
view(35, 30);

% 右侧：GD可视化（A→PF的距离）
subplot(1, 2, 2); hold on; grid on; axis equal;
scatter3(PF(:, 1), PF(:, 2), PF(:, 3), 15, [0.2 0.8 0.2], ...
         'filled', 'MarkerEdgeColor', 'k', 'DisplayName', '参考前沿(PF)');
scatter3(A(:, 1), A(:, 2), A(:, 3), 80, [0.9 0.2 0.2], ...
         'filled', 'MarkerEdgeColor', 'k', 'DisplayName', '近似解(A)');

% 绘制GD距离线（A到PF的最近距离）
for j = 1:size(A, 1)
    dists = sqrt(sum((PF - A(j, :)).^2, 2));
    [~, nearestIdx] = min(dists);
    plot3([A(j, 1), PF(nearestIdx, 1)], ...
          [A(j, 2), PF(nearestIdx, 2)], ...
          [A(j, 3), PF(nearestIdx, 3)], ...
          'm--', 'LineWidth', 0.5, 'HandleVisibility', 'off');
end
title(sprintf('GD 可视化 (值 = %.4f)', GD), 'FontSize', 12);
xlabel('f_1'); ylabel('f_2'); zlabel('f_3');
legend('Location', 'best');
view(35, 30);

hold off;

运行结果

三、GD vs IGD ------ 核心差异与适用场景

指标 计算方向 收敛性衡量 多样性衡量 适用场景
GD A → P F ′ A \to PF' A→PF′ 强 弱 初步评估算法收敛能力
IGD P F ′ → A PF' \to A PF′→A 强 强 全面评估算法（收敛+多样性）
关键结论
  • 若只需看算法是否"找得到好解"，用 GD；
  • 若需看算法是否"找到又好又全的解"，用 IGD；
  • 实际研究中，IGD 更常用，因为多目标优化追求"帕累托前沿的均匀覆盖"。

五、总结

GD 和 IGD 是多目标优化算法的"体检指标"：

  • GD 像"单科成绩"，只看收敛；
  • IGD 像"全科成绩"，看收敛+多样性。

在你的代码中，通过生成真实帕累托前沿 P F ′ PF' PF′，再遍历计算距离，即可量化评估算法性能。若研究多目标优化，IGD 几乎是必用指标。

相关推荐
007tg20 小时前
从ChatGPT家长控制功能看AI合规与技术应对策略
人工智能·chatgpt·企业数据安全
Memene摸鱼日报20 小时前
「Memene 摸鱼日报 2025.9.11」腾讯推出命令行编程工具 CodeBuddy Code, ChatGPT 开发者模式迎来 MCP 全面支持
人工智能·chatgpt·agi
linjoe9920 小时前
【Deep Learning】Ubuntu配置深度学习环境
人工智能·深度学习·ubuntu
Greedy Alg21 小时前
LeetCode 142. 环形链表 II
算法
睡不醒的kun21 小时前
leetcode算法刷题的第三十二天
数据结构·c++·算法·leetcode·职场和发展·贪心算法·动态规划
先做个垃圾出来………1 天前
残差连接的概念与作用
人工智能·算法·机器学习·语言模型·自然语言处理
AI小书房1 天前
【人工智能通识专栏】第十三讲：图像处理
人工智能
fanstuck1 天前
基于大模型的个性化推荐系统实现探索与应用
大数据·人工智能·语言模型·数据挖掘
SuperCandyXu1 天前
P3205 [HNOI2010] 合唱队-普及+/提高
c++·算法·洛谷
_OP_CHEN1 天前
数据结构（C语言篇）：（十二）实现顺序结构二叉树——堆
c语言·数据结构·算法·二叉树·学习笔记·堆·顺序结构二叉树
热门推荐
01KGG转MP3工具|非KGM文件|解密音频02GitHub 镜像站点03conda中设置镜像地址（附所有可换的地址）04UV安装并设置国内源0546个Nano-banana 精选提示词，持续更新中06A股预测还能更准？开源大模型Kronos带你跑通预测+回测全流程07UV 工具安装与国内镜像源配置指南08突破百度网盘的下载限速，两种方法教会你【超详细】09SQLmap 完整使用指南：环境搭建 + 命令详解 + 实操案例10教你如何认证 Gemini 教育优惠的二次验证，薅个 1年的 Gemini Pro 会员