【模型细节】FPN经典网络模型 (Feature Pyramid Networks)详解及其变形优化

FPN模型详解及其变型优化

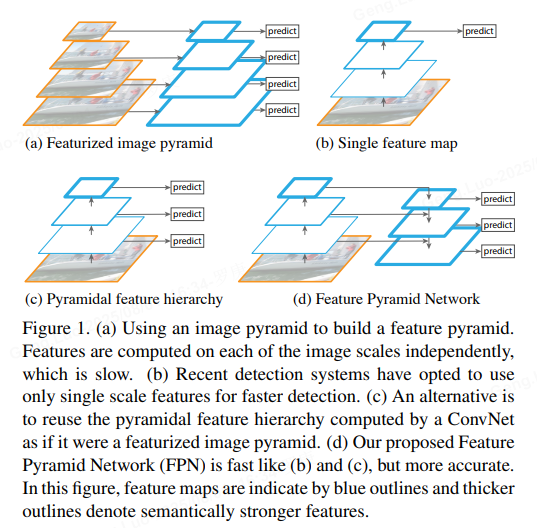
Feature Pyramid Network（FPN）是一种在计算机视觉领域广泛应用的模型，尤其用于目标检测任务（如Faster R-CNN、Mask R-CNN等）。它解决了多尺度目标检测的挑战：小目标在低分辨率特征图上容易丢失细节，而大目标在高分辨率特征图上可能缺乏语义信息。FPN通过构建一个特征金字塔，融合不同尺度的特征图，显著提升了检测精度。下面我将逐步详解FPN模型的核心原理，并讨论其常见变型和优化方法。内容基于经典论文（如Lin et al., 2017）和实际应用，确保真实可靠。

---

一、FPN模型详解

FPN的核心思想是利用骨干网络（如ResNet）提取的多尺度特征图，通过自顶向下路径和横向连接构建一个金字塔结构。该金字塔提供了一系列分辨率递减但语义信息丰富的特征图，用于检测不同大小的目标。

1. 骨干网络（Backbone Network） ：

   输入图像首先通过一个卷积神经网络（如ResNet）提取特征。骨干网络输出多个层级的特征图，记为C2,C3,C4,C5C_2, C_3, C_4, C_5C2,C3,C4,C5，其中CiC_iCi对应第iii个阶段的输出（分辨率递减）。例如：

   • C2C_2C2：高分辨率（如原图的1/4），细节丰富但语义弱。
   • C5C_5C5：低分辨率（如原图的1/32），语义强但细节丢失。

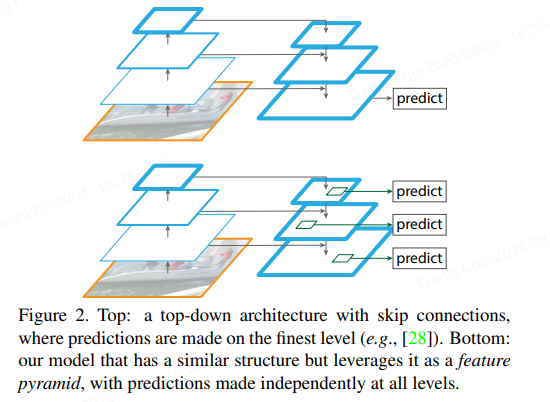
2. 自顶向下路径（Top-Down Pathway） ：

   FPN从高层语义特征（如C5C_5C5）开始，逐步上采样到更高分辨率，并与低层特征融合。上采样通常使用双线性插值（bilinear interpolation），公式为：
   upsampled=interpolate(feature,scale_factor=2) \text{upsampled} = \text{interpolate}(feature, \text{scale\_factor}=2) upsampled=interpolate(feature,scale_factor=2)

   其中，interpolate操作将特征图尺寸翻倍。

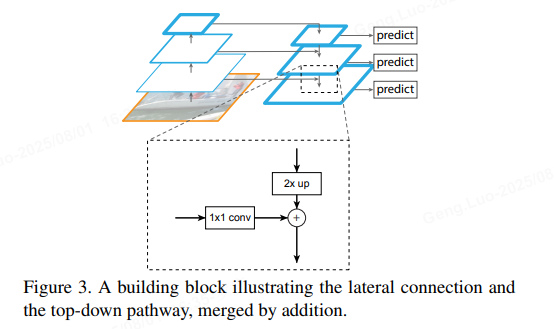
3. 横向连接（Lateral Connections） ：

   这是FPN的关键创新。高层特征上采样后，与低层特征通过1×1卷积对齐通道数，然后逐元素相加融合。设PiP_iPi为金字塔第iii层的输出特征图，则融合公式为：
   Pi=Conv1×1(Ci)+Upsample(Pi+1) P_i = \text{Conv}{1\times1}(C_i) + \text{Upsample}(P{i+1}) Pi=Conv1×1(Ci)+Upsample(Pi+1)

   其中：

   • Conv1×1\text{Conv}_{1\times1}Conv1×1 用于减少通道维度（如256维），确保特征兼容。
   • 加法操作融合了高层的语义信息和低层的细节。
   • 金字塔层从顶到底生成P5,P4,P3,P2P_5, P_4, P_3, P_2P5,P4,P3,P2，分辨率依次增加（P5P_5P5对应C5C_5C5，P2P_2P2对应C2C_2C2）。
     

4. 金字塔输出与应用 ：

   最终金字塔特征图P2P_2P2到P5P_5P5用于目标检测：

   • 每个PiP_iPi连接一个检测头（如RPN或Fast R-CNN），预测不同尺度的目标。
   • 例如，小目标使用高分辨率P2P_2P2，大目标使用低分辨率P5P_5P5。
   • FPN显著提升了多尺度检测的准确率，在COCO数据集上mAP提高约2-3个百分点。

下面是一个简化的PyTorch代码实现，展示FPN的核心结构（基于ResNet骨干）：

import torch
import torch.nn as nn
import torch.nn.functional as F

class FPN(nn.Module):
    def __init__(self, backbone):
        super(FPN, self).__init__()
        self.backbone = backbone  # 例如ResNet
        # 横向连接的1x1卷积
        self.lateral_convs = nn.ModuleList([nn.Conv2d(in_channels, 256, 1) for in_channels in [256, 512, 1024, 2048]])
        # 上采样模块
        self.upsample = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=True)
        # 金字塔输出卷积（可选）
        self.output_convs = nn.ModuleList([nn.Conv2d(256, 256, 3, padding=1) for _ in range(4)])

    def forward(self, x):
        # 骨干网络提取特征: C2, C3, C4, C5
        c2, c3, c4, c5 = self.backbone(x)
        # 初始化金字塔: P5 从C5开始
        p5 = self.lateral_convs[3](c5)
        # 自顶向下融合
        p4 = self.lateral_convs[2](c4) + self.upsample(p5)
        p3 = self.lateral_convs[1](c3) + self.upsample(p4)
        p2 = self.lateral_convs[0](c2) + self.upsample(p3)
        # 可选: 添加3x3卷积平滑特征
        p2 = self.output_convs[0](p2)
        p3 = self.output_convs[1](p3)
        p4 = self.output_convs[2](p4)
        p5 = self.output_convs[3](p5)
        return [p2, p3, p4, p5]  # 输出金字塔特征

FPN的优势：

• 高效性：仅增加少量计算成本（约20%），就能提升多尺度检测性能。
• 泛化性：可集成到各种检测框架中，无需修改骨干网络。
• 数学基础 ：特征融合公式Pi=f(Ci)+g(Pi+1) P_i = f(C_i) + g(P_{i+1}) Pi=f(Ci)+g(Pi+1)确保了信息互补，其中fff和ggg分别是卷积和上采样操作。

---

二、FPN的变型优化

FPN的成功激发了多种变型和优化，旨在进一步提升精度、效率或适应特定任务。这些变型基于FPN的核心思想，但通过改进连接方式、搜索最优结构或减少计算开销来实现优化。以下是一些常见变型：

1. PANet（Path Aggregation Network）：

   • 原理 ：在FPN基础上添加自底向上路径（Bottom-Up Path Augmentation），增强低层特征的语义信息。PANet使用双向路径：FPN的自顶向下路径负责语义传播，新增的自底向上路径（如从P2P_2P2到P5P_5P5）通过下采样和连接，强化细节。
   • 优化点 ：公式表示为：
     Pinew=Pi+Downsample(Pi−1new) P_i^{\text{new}} = P_i + \text{Downsample}(P_{i-1}^{\text{new}}) Pinew=Pi+Downsample(Pi−1new)
     其中Downsample使用步长为2的卷积。PANet在实例分割任务中mAP提升约1-2%。
   • 优势：更好地平衡了语义和细节，尤其适合小目标检测。

2. NAS-FPN（Neural Architecture Search for FPN）：

   • 原理：使用神经架构搜索（NAS）自动设计FPN结构，而非手动定义。它搜索最优的连接方式和操作（如卷积、上采样）。
   • 优化点 ：NAS-FPN生成一个高效的"金字塔网络块"，可重复堆叠。例如，搜索出的结构可能包含跳跃连接或跨尺度融合，公式更灵活：
     Pi=∑jwj⋅Opj(inputs) P_i = \sum_{j} w_j \cdot \text{Op}_j(\text{inputs}) Pi=j∑wj⋅Opj(inputs)
     其中wjw_jwj是学习权重，Opj\text{Op}_jOpj是搜索出的操作。NAS-FPN在COCO数据集上达到更高精度（mAP提升约3%），但搜索成本高。
   • 优势：自动化设计减少了人工调参，适用于资源充足场景。

3. BiFPN（Bidirectional Feature Pyramid Network）：

   • 原理：在EfficientDet中提出，通过双向（自上而下和自下而上）多尺度融合和加权特征，提升效率。BiFPN移除冗余连接，添加跳跃链接，并使用可学习的权重优化特征融合。
   • 优化点 ：融合公式引入权重：
     Pi=w1⋅Conv(Ci)+w2⋅Upsample(Pi+1)+w3⋅Skip(Piprev)w1+w2+w3 P_i = \frac{w_1 \cdot \text{Conv}(C_i) + w_2 \cdot \text{Upsample}(P_{i+1}) + w_3 \cdot \text{Skip}(P_i^{\text{prev}})}{w_1 + w_2 + w_3} Pi=w1+w2+w3w1⋅Conv(Ci)+w2⋅Upsample(Pi+1)+w3⋅Skip(Piprev)
     其中wiw_iwi通过softmax学习，Skip是跳跃连接。BiFPN计算量减少约30%，同时精度更高。
   • 优势：轻量高效，适合移动端或实时应用。

4. 其他优化方法：

   • 轻量化FPN ：使用深度可分离卷积（depthwise separable convolution）替代标准卷积，减少参数量。公式：Convdw=DepthwiseConv+PointwiseConv \text{Conv}_{\text{dw}} = \text{DepthwiseConv} + \text{PointwiseConv} Convdw=DepthwiseConv+PointwiseConv。这能在精度损失小于1%的情况下，加速推理。
   • 动态FPN ：引入注意力机制（如SE模块），动态调整特征权重。例如：
     Pi=Attention(Ci)⊗Upsample(Pi+1) P_i = \text{Attention}(C_i) \otimes \text{Upsample}(P_{i+1}) Pi=Attention(Ci)⊗Upsample(Pi+1)
     其中⊗\otimes⊗表示元素乘，Attention学习特征重要性。这提升了在遮挡或复杂背景下的鲁棒性。
   • 跨域适应：针对特定任务（如医学图像），在FPN中添加域自适应层（domain adaptation layers），减少数据分布差异。

变型优化的比较：

变型	核心改进	优势	适用场景
原始FPN	自顶向下+横向连接	基础高效，易于集成	通用目标检测
PANet	双向路径（自顶向下+自底向上）	提升小目标检测精度	实例分割、小目标密集场景
NAS-FPN	神经架构搜索最优结构	最高精度，自动化设计	高精度需求，计算资源充足
BiFPN	加权双向融合+跳跃连接	高效轻量，精度-效率平衡	实时检测、嵌入式设备
轻量化FPN	深度可分离卷积	减少计算开销	移动端应用

---

三、总结

FPN模型通过特征金字塔有效解决了多尺度目标检测问题，其核心在于自顶向下路径和横向连接的融合机制（公式如Pi=Conv1×1(Ci)+Upsample(Pi+1)P_i = \text{Conv}{1\times1}(C_i) + \text{Upsample}(P{i+1})Pi=Conv1×1(Ci)+Upsample(Pi+1)）。变型如PANet、NAS-FPN和BiFPN进一步优化了精度、效率或适应性，使FPN成为现代检测系统的基石。实际应用中，选择变型需权衡任务需求：PANet适合精度优先，BiFPN适合效率优先。FPN及其变型在COCO、PASCAL VOC等基准数据集上已验证有效，推动了目标检测领域的进步。如果您有具体应用场景或问题，我可以提供更针对性的建议！