【深度学习②】| DNN篇

0 序言

本文将系统介绍基于PyTorch的深度神经网络（DNN）相关知识 ，包括张量的基础操作、DNN的工作原理、实现流程，以及批量梯度下降、小批量梯度下降方法和手写数字识别案例。通过学习，你将掌握DNN的核心概念 、PyTorch实操技能，理解从数据处理到模型训练、测试的完整流程，具备搭建和应用简单DNN模型的能力。

1 张量

在深度学习中，数据的表示与处理是所有操作的基础。张量作为PyTorch中最核心的数据结构，承载着数据存储与计算的功能，是构建神经网络、实现模型训练的前提。因此，我们首先从张量的基本概念和操作入手。

1.1 数组与张量

NumPy的数组和PyTorch的张量是数据处理的核心结构，二者在语法上高度相似，但张量支持GPU加速 ，更适用于深度学习。因此在学习本小节前，如果你没有NumPy数组的相关基础，点此链接先学习后再学习本文：深度学习①-NumPy数组篇

对应关系 ：np对应torch，数组array对应张量tensor，n维数组对应n阶张量。
转换方法 ：
1.数组转张量 ：ts = torch.tensor(arr)
2.张量转数组 ：arr = np.array(ts)

1.2 从数组到张量

PyTorch在NumPy基础上修改了部分函数或方法，主要差异见下表：

NumPy的函数	PyTorch的函数	用法区别
`.astype()`	`.type()`	无
`np.random.random()`	`torch.rand()`	无
`np.random.randint()`	`torch.randint()`	不接纳一维张量
`np.random.normal()`	`torch.normal()`	不接纳一维张量
`np.random.randn()`	`torch.randn()`	无
`.copy()`	`.clone()`	无
`np.concatenate()`	`torch.cat()`	无
`np.split()`	`torch.split()`	参数含义优化
`np.dot()`	`torch.matmul()`	无
`np.dot(v,v)`	`torch.dot()`	无
`np.dot(m,v)`	`torch.mv()`	无
`np.dot(m,m)`	`torch.mm()`	无
`np.exp()`	`torch.exp()`	必须传入张量
`np.log()`	`torch.log()`	必须传入张量
`np.mean()`	`torch.mean()`	必须传入浮点型张量
`np.std()`	`torch.std()`	必须传入浮点型张量

1.3 用GPU存储张量

默认情况下，张量存储在CPU中，而GPU能显著提升计算速度，因此需掌握张量和模型的GPU迁移方法。

张量迁移到GPU ：

python 复制代码

import torch
ts1 = torch.randn(3,4)  # 存储在CPU
ts2 = ts1.to('cuda:0')  # 迁移到第一块GPU（cuda:0）

模型迁移到GPU ：

python 复制代码

class DNN(torch.nn.Module):  # 定义神经网络类
    pass  # 具体结构略
model = DNN().to('cuda:0')  # 模型迁移到GPU

查看GPU运行情况 ：在cmd中输入nvidia-smi，可查看显卡型号、内存使用等信息。当然了，硬件设备没有GPU的直接用CPU也行，速度慢一些，如果你电脑里有多个显卡，那你可以迁移到多块上，比如会有cuda：1、cuda：2等等。

2 DNN的原理

上一章介绍了数据的基础载体，也就是张量，而深度神经网络的核心是通过学习数据特征拟合输入与输出的关系 。本章将解析DNN的工作原理，包括数据集处理、训练、测试和使用的完整流程。

2.1 划分数据集

数据集是模型学习的基础，需包含输入特征和输出特征，并划分为训练集（用于模型学习）和测试集（用于验证模型泛化能力）。

划分原则：通常按7:3或8:2的比例划分，如1000个样本中800个为训练集，200个为测试集。
对应关系：输入特征的数量决定输入层神经元数，输出特征的数量决定输出层神经元数（例如：3个输入特征→输入层3个神经元，3个输出特征→输出层3个神经元）。

2.2 训练网络

训练是DNN优化内部参数（权重和偏置）的过程，通过前向传播计算预测值，再通过反向传播调整参数，最终拟合函数。

2.2.1 前向传播

输入特征从输入层逐层传递到输出层，每个神经元的计算为：

线性计算 ： y = ω 1 x 1 + ω 2 x 2 + . . . + ω n x n + b y = \omega_1 x_1 + \omega_2 x_2 + ... + \omega_n x_n + b y=ω1x1+ω2x2+...+ωnxn+b
其中， ω \omega ω为权重， b b b为偏置
非线性转换 ： y = σ ( 线性计算结果 ) y = \sigma(\text{线性计算结果}) y=σ(线性计算结果)
其中， σ \sigma σ为激活函数，如ReLU、Sigmoid，用于引入非线性，避免多层网络等效于单层）

2.2.2 反向传播

通过损失函数计算预测值与真实值的差距，再反向求解梯度 ，调整权重和偏置以减小损失。

损失函数：衡量预测误差（如MSE、BCELoss）。
学习率 ：控制参数调整幅度，过大可能导致损失震荡，过小则收敛缓慢。

2.2.3 batch_size

每次前向传播和反向传播的样本数量，影响训练效率和稳定性：

批量梯度下降（BGD）：一次输入所有样本，计算量大、速度慢。
随机梯度下降（SGD）：一次输入1个样本，速度快但收敛不稳定。
小批量梯度下降（MBGD）：一次输入若干样本（如32、64），平衡效率和稳定性，常用且batch_size通常设为2的幂次方。

2.2.4 epochs

全部样本完成一次前向和反向传播的次数。例：10240个样本，batch_size=1024，则1个epoch包含10240/1024=10次传播，5个epoch共50次传播。

2.3 测试网络

测试用于验证模型的泛化能力 ，避免过拟合，

过拟合就是模型仅适配训练集，对新数据无效。

比如说在训练集准确率能到100%，但是到新数据集只有50-60%这种情况。

解决方法：用测试集输入进行前向传播，对比预测输出与真实输出，计算准确率。

2.4 使用网络

训练好的模型可用于新数据预测，只需输入新样本的特征，通过一次前向传播得到输出。

3 DNN的实现

掌握了DNN的原理后，本章将通过PyTorch实操实现一个完整的DNN模型，包括数据集制作 、网络搭建 、训练、测试及模型保存。

3.1 制作数据集

需生成包含输入和输出特征的样本，并划分训练集和测试集。

python 复制代码

import torch

# 生成10000个样本，3个输入特征（均匀分布），3个输出特征（One-Hot编码）
X1 = torch.rand(10000, 1)
X2 = torch.rand(10000, 1)
X3 = torch.rand(10000, 1)
Y1 = ((X1 + X2 + X3) < 1).float()
Y2 = ((1 < (X1 + X2 + X3)) & ((X1 + X2 + X3) < 2)).float()
Y3 = ((X1 + X2 + X3) > 2).float()

# 整合数据集并迁移到GPU
Data = torch.cat([X1, X2, X3, Y1, Y2, Y3], axis=1).to('cuda:0')

# 划分训练集（70%）和测试集（30%）
Data = Data[torch.randperm(Data.size(0)), :]  # 打乱顺序
train_size = int(len(Data) * 0.7)
train_Data = Data[:train_size, :]
test_Data = Data[train_size:, :]

3.2 搭建神经网络

基于torch.nn.Module构建网络，需定义__init__（网络结构）和forward（前向传播）方法。

python 复制代码

import torch.nn as nn

class DNN(nn.Module):
    def __init__(self):
        super(DNN, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(3, 5), nn.ReLU(),  # 输入层→隐藏层1（3→5神经元，ReLU激活）
            nn.Linear(5, 5), nn.ReLU(),  # 隐藏层1→隐藏层2
            nn.Linear(5, 5), nn.ReLU(),  # 隐藏层2→隐藏层3
            nn.Linear(5, 3)  # 隐藏层3→输出层（5→3神经元）
        )
    
    def forward(self, x):
        return self.net(x)  # 前向传播

# 创建模型并迁移到GPU
model = DNN().to('cuda:0')

其中，

python 复制代码

self.net = nn.Sequential(
    nn.Linear(3, 5), nn.ReLU(),  # 输入层→隐藏层1（3→5神经元，ReLU激活）
    nn.Linear(5, 5), nn.ReLU(),  # 隐藏层1→隐藏层2
    nn.Linear(5, 5), nn.ReLU(),  # 隐藏层2→隐藏层3
    nn.Linear(5, 3)  # 隐藏层3→输出层（5→3神经元）
)

以上程序的计算逻辑如下图：

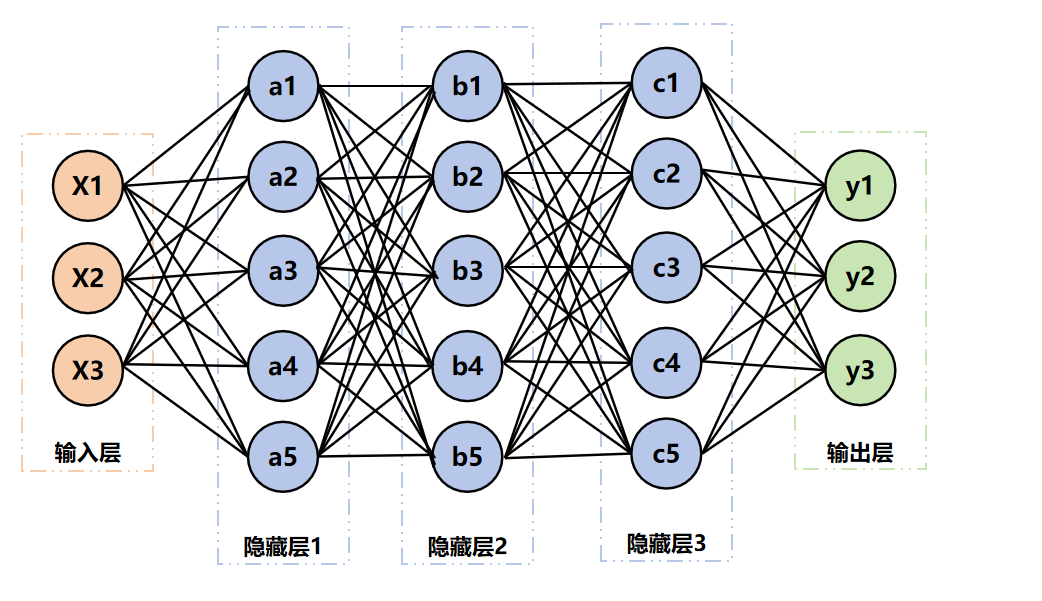
3.3 网络的内部参数

内部参数即权重（weight）和偏置（bias），初始为随机值（如Xavier、He初始值），训练中不断优化。

查看参数 ：

python 复制代码

for name, param in model.named_parameters():
    print(f"参数:{name}\n 形状:{param.shape}\n 数值:{param}\n")

参数特点 ：存储在GPU上（device='cuda:0'），且开启梯度计算（requires_grad=True）。

3.4 网络的外部参数

外部参数（超参数）需在训练前设定，包括：

网络结构：层数、隐藏层节点数、激活函数（如ReLU、Sigmoid）。
训练参数 ：损失函数（如nn.MSELoss()）、优化器（如torch.optim.SGD）、学习率、batch_size、epochs。

3.5 训练网络

通过多轮前向传播、损失计算、反向传播和参数优化，最小化损失。

python 复制代码

epochs = 1000
losses = []  # 记录损失变化
loss_fn = nn.MSELoss()  # 损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)  # 优化器

# 提取训练集输入和输出
X = train_Data[:, :3]
Y = train_Data[:, -3:]

for epoch in range(epochs):
    Pred = model(X)  # 前向传播
    loss = loss_fn(Pred, Y)  # 计算损失
    losses.append(loss.item())  # 记录损失
    optimizer.zero_grad()  # 清空梯度
    loss.backward()  # 反向传播
    optimizer.step()  # 更新参数

3.6 测试网络

关闭梯度计算，用测试集验证模型准确率。

python 复制代码

# 提取测试集输入和输出
X = test_Data[:, :3]
Y = test_Data[:, -3:]

with torch.no_grad():  # 关闭梯度
    Pred = model(X)  # 前向传播
    # 规整预测值（与真实值格式一致）
    Pred[:, torch.argmax(Pred, axis=1)] = 1
    Pred[Pred != 1] = 0
    # 计算准确率
    correct = torch.sum((Pred == Y).all(1))
    total = Y.size(0)
    print(f'测试集精准度: {100 * correct / total} %')

3.7 保存与导入网络

训练好的模型需保存，以便后续使用。

保存模型 ：torch.save(model, 'model.pth')
导入模型 ：new_model = torch.load('model.pth')
验证导入：用新模型测试，准确率应与原模型一致。

3.8 完整程序

这里演示的并未用到GPU。

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim

# ======================== 1. 制作数据集 ======================== #
# 生成3个输入特征（均匀分布在[0,1)），共10000个样本
X1 = torch.rand(10000, 1)  # 输入特征1
X2 = torch.rand(10000, 1)  # 输入特征2
X3 = torch.rand(10000, 1)  # 输入特征3

# 计算3个输出特征（One-Hot编码，对应和的三个区间）
sum_xy = X1 + X2 + X3
Y1 = (sum_xy < 1).float()          # 和 < 1 → 类别1
Y2 = ((sum_xy >= 1) & (sum_xy < 2)).float()  # 1 ≤ 和 < 2 → 类别2（修正边界，避免遗漏）
Y3 = (sum_xy >= 2).float()         # 和 ≥ 2 → 类别3

# 拼接输入和输出特征，形成完整数据集（共6列：3输入 + 3输出）
data = torch.cat([X1, X2, X3, Y1, Y2, Y3], dim=1)

# 打乱数据顺序（避免训练时样本顺序影响）
shuffled_index = torch.randperm(data.shape[0])  # 生成随机索引
data = data[shuffled_index]

# 划分训练集（70%）和测试集（30%）
train_size = int(len(data) * 0.7)
train_data = data[:train_size]
test_data = data[train_size:]


# ======================== 2. 搭建神经网络 ======================== #
class DNN(nn.Module):
    def __init__(self):
        super(DNN, self).__init__()
        # 构建网络：3层隐藏层，每层5个神经元，ReLU激活
        self.net = nn.Sequential(
            nn.Linear(3, 5),  # 输入层（3特征）→ 隐藏层1（5神经元）
            nn.ReLU(),        # 激活函数：引入非线性，避免网络退化为线性模型
            nn.Linear(5, 5),  # 隐藏层1 → 隐藏层2
            nn.ReLU(),
            nn.Linear(5, 5),  # 隐藏层2 → 隐藏层3
            nn.ReLU(),
            nn.Linear(5, 3)   # 隐藏层3 → 输出层（3类别，对应One-Hot编码）
        )
    
    def forward(self, x):
        """前向传播：输入数据→网络计算→输出预测值"""
        return self.net(x)

# 初始化模型（自动运行在CPU，因未指定设备）
model = DNN()


# ======================== 3. 定义训练参数 ======================== #
epochs = 1000                # 训练轮次：整个数据集遍历1000次
loss_fn = nn.MSELoss()       # 损失函数：均方误差（适合One-Hot编码的分类任务）
optimizer = optim.SGD(       # 优化器：随机梯度下降
    model.parameters(),      # 优化对象：模型的权重和偏置
    lr=0.01                  # 学习率：控制参数更新幅度（需根据任务调整）
)

# 提取训练集的输入（前3列）和输出（后3列）
X_train = train_data[:, :3]
Y_train = train_data[:, 3:]


# ======================== 4. 训练网络 ======================== #
loss_recorder = []  # 记录每轮损失，用于分析训练趋势
for epoch in range(epochs):
    # 1. 前向传播：用当前模型预测训练数据
    pred = model(X_train)
    
    # 2. 计算损失：预测值与真实值的差距
    loss = loss_fn(pred, Y_train)
    loss_recorder.append(loss.item())  # 保存损失值（转换为Python数值）
    
    # 3. 反向传播：计算梯度并更新参数
    optimizer.zero_grad()  # 清空上一轮的梯度（否则会累积，导致错误）
    loss.backward()        # 反向传播：自动计算参数的梯度
    optimizer.step()       # 根据梯度更新参数（权重和偏置）
    
    # 可选：每100轮打印训练进度
    if (epoch + 1) % 100 == 0:
        print(f"训练轮次: {epoch+1:4d} / {epochs}, 损失值: {loss.item():.6f}")


# ======================== 5. 测试网络 ======================== #
# 提取测试集的输入和输出
X_test = test_data[:, :3]
Y_test = test_data[:, 3:]

with torch.no_grad():  # 测试阶段无需计算梯度，加速运算并节省内存
    # 前向传播预测
    pred_test = model(X_test)
    
    # 将预测值规整为One-Hot格式（与真实标签一致）
    # 步骤：找到每个样本预测值最大的索引，将该位置设为1，其余设为0
    max_index = torch.argmax(pred_test, dim=1)  # 每个样本的最大概率类别索引
    pred_onehot = torch.zeros_like(pred_test)   # 初始化全0的One-Hot张量
    # 根据索引设置1（dim=1表示按列操作，unsqueeze将索引转为列向量）
    pred_onehot.scatter_(1, max_index.unsqueeze(1), 1)
    
    # 计算准确率：预测与真实完全匹配的样本数 ÷ 总样本数
    correct_count = torch.sum(torch.all(pred_onehot == Y_test, dim=1))  # 逐样本判断是否全对
    total_count = Y_test.shape[0]
    accuracy = 100 * correct_count / total_count
    print(f"\n测试集准确率: {accuracy:.2f} %")


# ======================== 6. 保存模型 ======================== #
torch.save(model, "dnn_model.pth")
print("模型已保存为 'dnn_model.pth'（可后续加载复用）")

运行结果如下：

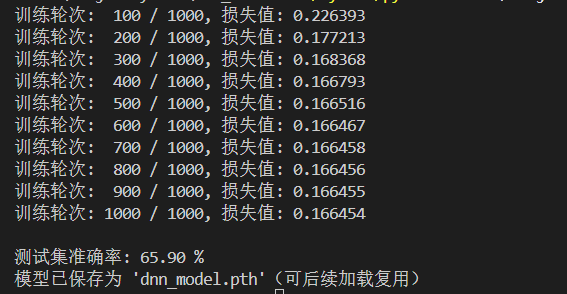
从最终结果上来看，损失从 0.226 逐步降至 0.166 ，符合梯度下降的收敛规律：

前期（1~300 轮）：损失快速下降 → 模型快速学习输入（X1/X2/X3）和输出（区间分类）的关联；

后期（300~1000 轮）：损失下降变缓 → 接近局部最优解，参数调整空间缩小

可以理解为模型学不动了。

最终损失仍较高，说明模型未完全拟合数据，

不过考虑到本次模型结构简单，我们只用了3 层隐藏层，每层仅 5 个神经元，再加上优化器（SGD）较基础，没有换更智能的优化器，所以这个结果也不意外。

4 批量梯度下降

上一章实现了基础DNN，但未明确梯度下降的批量处理方式。批量梯度下降（BGD）每次用全部样本更新参数，适用于小数据集。本章将完整演示其流程。

4.1 制作数据集

从Excel导入数据，转换为张量并划分训练集和测试集。

python 复制代码

import pandas as pd

# 导入数据并转换为张量
df = pd.read_csv('Data.csv', index_col=0)
arr = df.values.astype(np.float32)  # 转为float32避免类型冲突
ts = torch.tensor(arr).to('cuda')  # 迁移到GPU

# 划分训练集（70%）和测试集（30%）
ts = ts[torch.randperm(ts.size(0)), :]
train_size = int(len(ts) * 0.7)
train_Data = ts[:train_size, :]
test_Data = ts[train_size:, :]

4.2 搭建神经网络

输入特征为8个，输出特征为1个，网络结构如下：

python 复制代码

class DNN(nn.Module):
    def __init__(self):
        super(DNN, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(8, 32), nn.Sigmoid(),  # 8→32神经元，Sigmoid激活
            nn.Linear(32, 8), nn.Sigmoid(),
            nn.Linear(8, 4), nn.Sigmoid(),
            nn.Linear(4, 1), nn.Sigmoid()  # 输出层1个神经元
        )
    
    def forward(self, x):
        return self.net(x)

model = DNN().to('cuda:0')

这里的原理在上一节有做过图进行演示，道理是一样的。

python 复制代码

self.net = nn.Sequential(
    nn.Linear(8, 32), nn.Sigmoid(),  # 8→32神经元，Sigmoid激活
    nn.Linear(32, 8), nn.Sigmoid(),
    nn.Linear(8, 4), nn.Sigmoid(),
    nn.Linear(4, 1), nn.Sigmoid()  # 输出层1个神经元
)

然后这里使用sigmoid激活则是为引入非线性，避免多层线性层退化为单层，让网络学习复杂特征，虽然存在梯度消失缺陷，但因本网络隐藏层少、任务简单，故仍采用；

4.3 训练网络

使用BGD（每次输入全部训练样本）：

python 复制代码

loss_fn = nn.BCELoss(reduction='mean')  # 二分类损失函数
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)  # Adam优化器
epochs = 5000
losses = []

# 提取训练集输入和输出
X = train_Data[:, :-1]
Y = train_Data[:, -1].reshape((-1, 1))  # 调整输出形状

for epoch in range(epochs):
    Pred = model(X)
    loss = loss_fn(Pred, Y)
    losses.append(loss.item())
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

4.4 测试网络

python 复制代码

X = test_Data[:, :-1]
Y = test_Data[:, -1].reshape((-1, 1))

with torch.no_grad():
    Pred = model(X)
    Pred[Pred >= 0.5] = 1  # 预测值≥0.5视为1，否则为0
    Pred[Pred < 0.5] = 0
    correct = torch.sum((Pred == Y).all(1))
    total = Y.size(0)
    print(f'测试集精准度: {100 * correct / total} %')

4.5 完整程序

注意：这里仍然是用CPU来运行的，想改成GPU的，ts = torch.tensor(arr)这个程序指定好你得cuda即可，程序后面的也是如此。

python 复制代码

import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np  # 用于数组类型转换

# ======================== 1. 制作数据集 ======================== #
# 从xlsx读取数据
df = pd.read_excel(r'D:\ProjectPython\DNN_CNN\Data.xlsx', index_col=0,engine='openpyxl')  
# 转换为float32（PyTorch默认浮点类型，避免类型冲突）
arr = df.values.astype(np.float32)  
# 转换为PyTorch张量（自动运行在CPU，因未指定device）
ts = torch.tensor(arr)  

# 打乱数据顺序（避免训练时样本顺序影响模型学习）
shuffled_idx = torch.randperm(ts.size(0))  # 生成随机索引
ts = ts[shuffled_idx]

# 划分训练集（70%）和测试集（30%）
train_size = int(len(ts) * 0.7)
train_Data = ts[:train_size]  # 前70%为训练集
test_Data = ts[train_size:]   # 后30%为测试集


# ======================== 2. 搭建神经网络 ======================== #
class DNN(nn.Module):
    def __init__(self):
        super(DNN, self).__init__()
        # 构建4层全连接网络，Sigmoid作为激活函数
        self.net = nn.Sequential(
            # 输入层：8个特征 → 隐藏层1：32个神经元
            nn.Linear(8, 32), nn.Sigmoid(),  
            # 隐藏层1 → 隐藏层2：8个神经元
            nn.Linear(32, 8), nn.Sigmoid(),   
            # 隐藏层2 → 隐藏层3：4个神经元
            nn.Linear(8, 4), nn.Sigmoid(),    
            # 隐藏层3 → 输出层：1个神经元（输出概率，范围0~1）
            nn.Linear(4, 1), nn.Sigmoid()     
        )
    
    def forward(self, x):
        """前向传播：输入数据通过网络计算，返回预测概率"""
        return self.net(x)

# 初始化模型（自动运行在CPU）
model = DNN()  


# ======================== 3. 训练配置（超参数） ======================== #
loss_fn = nn.BCELoss(reduction='mean')  # 二分类交叉熵损失（适配Sigmoid的概率输出）
optimizer = optim.Adam(  # Adam优化器（收敛更快，适合演示）
    model.parameters(),  # 优化对象：模型的权重和偏置
    lr=0.005             # 学习率：控制参数更新幅度
)
epochs = 5000  # 训练轮次：整个训练集遍历5000次
losses = []    # 记录每轮损失，用于分析训练趋势


# ======================== 4. 训练网络 ======================== #
# 提取训练集的输入（前8列）和输出（最后1列，需调整形状为[batch, 1]）
X_train = train_Data[:, :-1]
Y_train = train_Data[:, -1].reshape(-1, 1)  # 确保输出是二维张量（匹配BCELoss输入要求）

for epoch in range(epochs):
    # 1. 前向传播：用当前模型预测训练数据
    pred = model(X_train)
    
    # 2. 计算损失：预测概率与真实标签的差距
    loss = loss_fn(pred, Y_train)
    losses.append(loss.item())  # 保存损失值（转换为Python原生浮点数）
    
    # 3. 反向传播 + 参数更新
    optimizer.zero_grad()  # 清空上一轮的梯度（否则会累积，导致错误）
    loss.backward()        # 自动计算参数的梯度（反向传播）
    optimizer.step()       # 根据梯度更新参数（权重和偏置）
    
    # 可选：每500轮打印训练进度（方便观察收敛情况）
    if (epoch + 1) % 500 == 0:
        print(f"训练轮次: {epoch+1:5d} / {epochs}, 当前损失: {loss.item():.6f}")


# ======================== 5. 测试网络 ======================== #
# 提取测试集的输入和输出（同样调整输出形状）
X_test = test_Data[:, :-1]
Y_test = test_Data[:, -1].reshape(-1, 1)

with torch.no_grad():  # 测试阶段无需计算梯度，提升效率并节省内存
    # 前向传播预测
    pred_test = model(X_test)
    
    # 将概率预测转换为0/1（≥0.5视为正类，<0.5视为负类）
    pred_test[pred_test >= 0.5] = 1.0
    pred_test[pred_test < 0.5] = 0.0
    
    # 计算准确率：预测与真实完全一致的样本数 ÷ 总样本数
    # torch.all(..., dim=1)：逐行判断所有列是否都匹配（此处仅1列，即判断单个值是否相等）
    correct_count = torch.sum(torch.all(pred_test == Y_test, dim=1))
    total_count = Y_test.size(0)
    accuracy = 100 * correct_count / total_count
    print(f"\n测试集准确率: {accuracy:.2f} %")

运行结果如下：

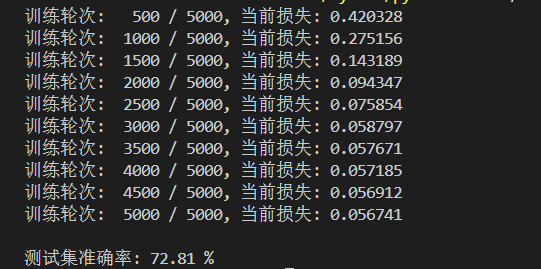
从输出的结果上来说，训练时损失从0.4203逐步降至0.0567，前期快速下降、后期收敛趋缓，体现模型有效学习数据关联但逼近优化瓶颈。后续可通过替换ReLU激活 、采用AdamW + 学习率调度优化训练、分析数据平衡与特征质量等方式突破性能瓶颈。

5 小批量梯度下降

批量梯度下降在大数据集上效率低，小批量梯度下降（MBGD）按批次输入样本，平衡效率和稳定性。本章将使用PyTorch的DataSet和DataLoader实现MBGD。

5.1 制作数据集

继承Dataset类封装数据，实现数据加载、索引获取和长度计算。

python 复制代码

from torch.utils.data import Dataset, DataLoader, random_split

class MyData(Dataset):
    def __init__(self, filepath):
        df = pd.read_csv(filepath, index_col=0)
        arr = df.values.astype(np.float32)
        ts = torch.tensor(arr).to('cuda')
        self.X = ts[:, :-1]  # 输入特征
        self.Y = ts[:, -1].reshape((-1, 1))  # 输出特征
        self.len = ts.shape[0]  # 样本总数
    
    def __getitem__(self, index):
        return self.X[index], self.Y[index]  # 获取索引对应的样本
    
    def __len__(self):
        return self.len  # 返回样本总数

# 划分训练集和测试集
Data = MyData('Data.csv')
train_size = int(len(Data) * 0.7)
test_size = len(Data) - train_size
train_Data, test_Data = random_split(Data, [train_size, test_size])

# 批次加载器（shuffle=True表示每个epoch前打乱数据）
train_loader = DataLoader(dataset=train_Data, shuffle=True, batch_size=128)
test_loader = DataLoader(dataset=test_Data, shuffle=False, batch_size=64)

5.2 搭建神经网络

与4.2节结构相同（输入8，输出1）。

5.3 训练网络

按批次输入样本进行训练：

python 复制代码

loss_fn = nn.BCELoss(reduction='mean')
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
epochs = 500
losses = []

for epoch in range(epochs):
    for (x, y) in train_loader:  # 按批次获取样本
        Pred = model(x)
        loss = loss_fn(Pred, y)
        losses.append(loss.item())
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

5.4 测试网络

按批次测试并计算总准确率：

python 复制代码

correct = 0
total = 0
with torch.no_grad():
    for (x, y) in test_loader:
        Pred = model(x)
        Pred[Pred >= 0.5] = 1
        Pred[Pred < 0.5] = 0
        correct += torch.sum((Pred == y).all(1))
        total += y.size(0)
print(f'测试集精准度: {100 * correct / total} %')

5.5 完整程序

python 复制代码

# 导入必要库
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader, random_split
import numpy as np


# ======================== 1. 自定义数据集类（支持.xlsx） ======================== #
class MyData(Dataset):
    def __init__(self, filepath):
        """
        初始化：读取Excel数据，转换为PyTorch张量（CPU）
        :param filepath: 数据集文件路径（.xlsx格式）
        """
        # 读取Excel（必须安装openpyxl！engine指定解析器）
        df = pd.read_excel(  
            filepath, 
            index_col=0,        # 第1列作为索引
            engine='openpyxl'   # 强制使用openpyxl解析.xlsx
        )  
        arr = df.values.astype(np.float32)  # 转换为float32（匹配PyTorch）
        ts = torch.tensor(arr)              # 转为CPU张量（未指定device的情况下不使用GPU）
        
        self.X = ts[:, :-1]  # 输入特征（前8列）
        self.Y = ts[:, -1].reshape(-1, 1)  # 输出标签（最后1列，调整为列向量）
        self.len = len(ts)   # 样本总数

    def __getitem__(self, index):
        """获取指定索引的样本：(输入特征, 输出标签)"""
        return self.X[index], self.Y[index]

    def __len__(self):
        """返回数据集总样本数"""
        return self.len


# ======================== 2. 加载并划分数据集 ======================== #
data_path = "Data.xlsx"  # 改为你的Excel文件路径（确保存在）
full_dataset = MyData(data_path)  # 初始化自定义数据集

# 划分训练集（70%）和测试集（30%）
train_size = int(0.7 * len(full_dataset))
test_size = len(full_dataset) - train_size
train_dataset, test_dataset = random_split(full_dataset, [train_size, test_size])

# 创建数据加载器（小批量读取）
batch_size = 128  # 小批量大小（可调整，建议2的幂次）
train_loader = DataLoader(
    train_dataset, 
    batch_size=batch_size, 
    shuffle=True  # 训练集每个epoch前打乱
)
test_loader = DataLoader(
    test_dataset, 
    batch_size=64, 
    shuffle=False  # 测试集保持顺序，方便复现
)


# ======================== 3. 定义神经网络模型 ======================== #
class DNN(nn.Module):
    def __init__(self):
        super(DNN, self).__init__()
        # 4层全连接网络，Sigmoid激活（输出层适配二分类）
        self.net = nn.Sequential(
            nn.Linear(8, 32), nn.Sigmoid(),  # 8→32
            nn.Linear(32, 8), nn.Sigmoid(),   # 32→8
            nn.Linear(8, 4), nn.Sigmoid(),    # 8→4
            nn.Linear(4, 1), nn.Sigmoid()     # 4→1（输出0~1概率）
        )

    def forward(self, x):
        """前向传播：输入→网络→预测概率"""
        return self.net(x)

model = DNN()  # CPU运行


# ======================== 4. 训练配置（损失函数 + 优化器） ======================== #
loss_fn = nn.BCELoss(reduction='mean')  # 二分类交叉熵损失
optimizer = optim.Adam(model.parameters(), lr=0.005)  # Adam优化器
epochs = 500  # 训练轮次
losses = []   # 记录batch级损失


# ======================== 5. 小批量训练（MBGD） ======================== #
for epoch in range(epochs):
    for batch_idx, (x, y) in enumerate(train_loader):
        # 1. 前向传播
        pred = model(x)
        
        # 2. 计算损失
        loss = loss_fn(pred, y)
        losses.append(loss.item())
        
        # 3. 反向传播 + 更新参数
        optimizer.zero_grad()  # 清空梯度
        loss.backward()        # 计算梯度
        optimizer.step()       # 更新参数
    
    # 每100轮打印进度
    if (epoch + 1) % 100 == 0:
        print(f"训练轮次: {epoch+1:4d} / {epochs}, 最近批次损失: {loss.item():.6f}")


# ======================== 6. 测试网络 ======================== #
correct = 0
total = 0

with torch.no_grad():  # 关闭梯度，加速测试
    for x, y in test_loader:
        pred = model(x)
        # 概率→0/1（阈值0.5）
        pred[pred >= 0.5] = 1.0
        pred[pred < 0.5] = 0.0
        
        # 统计正确数（逐样本判断）
        batch_correct = torch.sum(torch.all(pred == y, dim=1))
        correct += batch_correct.item()
        total += y.size(0)

accuracy = 100 * correct / total
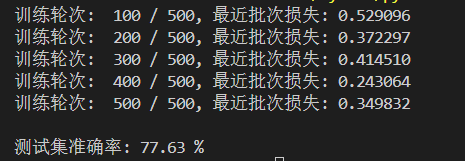
print(f"\n测试集准确率: {accuracy:.2f} %")

运行结果如下：

6 手写数字识别

前几章介绍了通用DNN的实现，本章以**MNIST数据集（手写数字图像）**为例，展示DNN在图像分类任务中的应用。

6.1 制作数据集

使用torchvision下载MNIST数据集，转换为张量并标准化。

python 复制代码

from torchvision import transforms, datasets

# 数据转换：转为张量并标准化（均值0.1307，标准差0.3081）
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize(0.1307, 0.3081)
])

# 下载训练集和测试集
train_Data = datasets.MNIST(
    root='D:/Jupyter/dataset/mnist/',
    train=True, download=True, transform=transform
)
test_Data = datasets.MNIST(
    root='D:/Jupyter/dataset/mnist/',
    train=False, download=True, transform=transform
)

# 批次加载器
train_loader = DataLoader(train_Data, shuffle=True, batch_size=64)
test_loader = DataLoader(test_Data, shuffle=False, batch_size=64)

6.2 搭建神经网络

输入为28×28的图像（展平为784维），输出为10个数字（0-9）：

python 复制代码

class DNN(nn.Module):
    def __init__(self):
        super(DNN, self).__init__()
        self.net = nn.Sequential(
            nn.Flatten(),  # 展平图像为784维向量
            nn.Linear(784, 512), nn.ReLU(),
            nn.Linear(512, 256), nn.ReLU(),
            nn.Linear(256, 128), nn.ReLU(),
            nn.Linear(128, 64), nn.ReLU(),
            nn.Linear(64, 10)  # 输出10个类别
        )
    
    def forward(self, x):
        return self.net(x)

model = DNN().to('cuda:0')

6.3 训练网络

使用交叉熵损失（自带softmax激活）和带动量的SGD优化器：

python 复制代码

loss_fn = nn.CrossEntropyLoss()  # 多分类损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 动量参数
epochs = 5
losses = []

for epoch in range(epochs):
    for (x, y) in train_loader:
        x, y = x.to('cuda:0'), y.to('cuda:0')  # 迁移到GPU
        Pred = model(x)
        loss = loss_fn(Pred, y)
        losses.append(loss.item())
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

6.4 测试网络

python 复制代码

correct = 0
total = 0
with torch.no_grad():
    for (x, y) in test_loader:
        x, y = x.to('cuda:0'), y.to('cuda:0')
        Pred = model(x)
        _, predicted = torch.max(Pred.data, dim=1)  # 获取预测类别（最大值索引）
        correct += torch.sum(predicted == y)
        total += y.size(0)
print(f'测试集精准度: {100 * correct / total} %')

6.5 完整程序

python 复制代码

# 导入核心库
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import transforms, datasets  # 用于加载MNIST数据集
from torch.utils.data import DataLoader       # 用于批量加载数据


# ======================== 1. 数据集准备（MNIST） ======================== #
# 数据预处理：转为张量 + 标准化（均值和标准差是MNIST的统计特征，加速训练收敛）
transform = transforms.Compose([
    transforms.ToTensor(),  # 将PIL图像转为张量（自动缩放到[0,1]）
    transforms.Normalize(   # 标准化：(x-mean)/std，减少数据分布差异对训练的影响
        mean=0.1307,        # MNIST像素均值（官方推荐的参数）
        std=0.3081          # MNIST像素标准差（官方推荐的参数）
    )
])

# 下载并加载训练集（自动下载到root目录，train=True表示训练集）
train_dataset = datasets.MNIST(
    root='./data/mnist',     # 数据保存路径（不存在则自动创建）
    train=True,              # 加载训练集
    download=True,           # 自动下载
    transform=transform      # 应用预处理
)

# 下载并加载测试集（train=False表示测试集）
test_dataset = datasets.MNIST(
    root='./data/mnist',     
    train=False,             
    download=True,           
    transform=transform      
)

# 创建批量加载器（小批量梯度下降，提升效率）
batch_size = 64  # 每批64张图像
train_loader = DataLoader(
    train_dataset, 
    batch_size=batch_size, 
    shuffle=True  # 训练集打乱，增加随机性
)
test_loader = DataLoader(
    test_dataset, 
    batch_size=batch_size, 
    shuffle=False  # 测试集保持顺序，方便结果复现
)


# ======================== 2. 定义神经网络模型 ======================== #
class DNN(nn.Module):
    def __init__(self):
        super(DNN, self).__init__()
        self.net = nn.Sequential(
            nn.Flatten(),  # 将28×28的图像展平为784维向量（28*28=784）
            # 全连接层 + ReLU激活（逐步压缩特征维度）
            nn.Linear(784, 512), nn.ReLU(),  # 784→512
            nn.Linear(512, 256), nn.ReLU(),  # 512→256
            nn.Linear(256, 128), nn.ReLU(),  # 256→128
            nn.Linear(128, 64),  nn.ReLU(),  # 128→64
            nn.Linear(64, 10)                # 64→10（输出10个数字的预测概率）
        )
    
    def forward(self, x):
        """前向传播：输入图像→网络→10类预测概率"""
        return self.net(x)

# 初始化模型（默认运行在CPU，无需显式指定设备）
model = DNN()  


# ======================== 3. 训练配置（损失函数 + 优化器） ======================== #
loss_fn = nn.CrossEntropyLoss()  # 多分类交叉熵损失（自带Softmax，输出层无需激活）
optimizer = optim.SGD(           # 带动量的随机梯度下降（加速收敛）
    model.parameters(),          # 优化对象：模型参数
    lr=0.01,                     # 学习率
    momentum=0.5                 # 动量（利用历史梯度加速更新）
)
epochs = 5  # 训练轮次（遍历整个训练集5次）


# ======================== 4. 训练网络 ======================== #
for epoch in range(epochs):
    # 遍历训练集的每个批次
    for batch_idx, (images, labels) in enumerate(train_loader):
        # 1. 前向传播：计算当前批次的预测概率
        outputs = model(images)
        
        # 2. 计算损失：预测与真实标签的差距
        loss = loss_fn(outputs, labels)
        
        # 3. 反向传播 + 参数更新
        optimizer.zero_grad()  # 清空上一轮梯度
        loss.backward()        # 反向传播计算梯度
        optimizer.step()       # 更新模型参数
    
    # 每轮结束打印进度（观察损失变化，可选）
    print(f"训练轮次: {epoch+1}/{epochs}, 最近批次损失: {loss.item():.4f}")


# ======================== 5. 测试网络 ======================== #
correct = 0  # 正确预测的样本数
total = 0    # 测试集总样本数

with torch.no_grad():  # 测试阶段关闭梯度计算，提升效率
    for images, labels in test_loader:
        # 前向传播预测
        outputs = model(images)
        # 获取预测类别（取概率最大的索引，dim=1表示按行取最大值）
        _, predicted = torch.max(outputs.data, dim=1)
        
        # 统计正确数和总数
        correct += (predicted == labels).sum().item()
        total += labels.size(0)

# 计算准确率
accuracy = 100 * correct / total
print(f"\n测试集准确率: {accuracy:.2f} %")

运行结果如下：

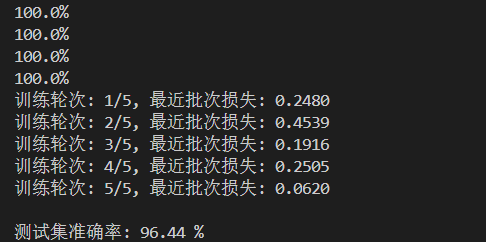
训练中损失从0.2480震荡降至0.0620，体现模型有效学习但受小批量随机性影响；测试集96.44%准确率达到DNN基线，证明能够很好地去捕捉数字特征却存在提升空间。可通过延长训练轮次、换Adam优化器/加学习率调度加速收敛，或升级为CNN利用图像空间关联，突破性能瓶颈。不过这个准确率已经算是可以了。

7 小结

本文系统介绍了PyTorch实现深度神经网络（DNN）的全流程，核心内容包括：

张量操作：作为数据载体，需掌握与NumPy的转换、GPU迁移及函数差异。
DNN原理：通过数据集划分、前向/反向传播、参数优化实现模型训练，理解batch_size和epochs的作用。
实现流程 ：从数据集制作、网络搭建（基于nn.Module）、训练（损失函数+优化器）到测试，完整覆盖模型生命周期。
梯度下降方法 ：对比批量（BGD）和小批量（MBGD）的适用场景，掌握DataSet和DataLoader的使用。
实战案例：MNIST手写数字识别展示了DNN在图像分类中的应用，涉及数据预处理和多分类损失函数。

通过学习，可掌握DNN的核心概念和PyTorch实操技能，为更复杂的深度学习模型（如CNN、RNN）做好准备，另外就是文章内的程序都是用CPU跑的，也不需要跑很长时间就可以完成模型的训练并看到结果。