文章目录
- 机械学习
-
- 机械学习分类
-
-
- [1. 监督学习](#1. 监督学习)
- [2. 半监督学习](#2. 半监督学习)
- [3. 无监督学习](#3. 无监督学习)
- [4. 强化学习](#4. 强化学习)
-
- 机械学习的项目开发步骤
- scikit-learn
- 特征工程
-
- [1 DictVectorizer - 字典列表特征提取](#1 DictVectorizer - 字典列表特征提取)
- [2 CountVectorizer - 文本特征提取](#2 CountVectorizer - 文本特征提取)
- [3 TfidfVectorizer TF-IDF - 文本特征词的重要程度特征提取](#3 TfidfVectorizer TF-IDF - 文本特征词的重要程度特征提取)
- [4 无量纲化-预处理](#4 无量纲化-预处理)
-
- [1. MaxAbsScaler](#1. MaxAbsScaler)
- [2. normalize归一化](#2. normalize归一化)
- [3. StandardScaler](#3. StandardScaler)
- 特征降维
-
-
- [1 特征选择](#1 特征选择)
- [2 主成分分析(PCA)](#2 主成分分析(PCA))
-
机械学习
机器学习(Machine Learning, ML)是人工智能(AI)的核心分支之一,其核心思想是让计算机通过对数据的学习,自动发现规律、改进性能,并用于解决预测、决策、模式识别等问题。与传统编程 "手动编写规则" 不同,机器学习通过算法从数据中 "自主学习" 规律,实现对未知数据的有效处理。
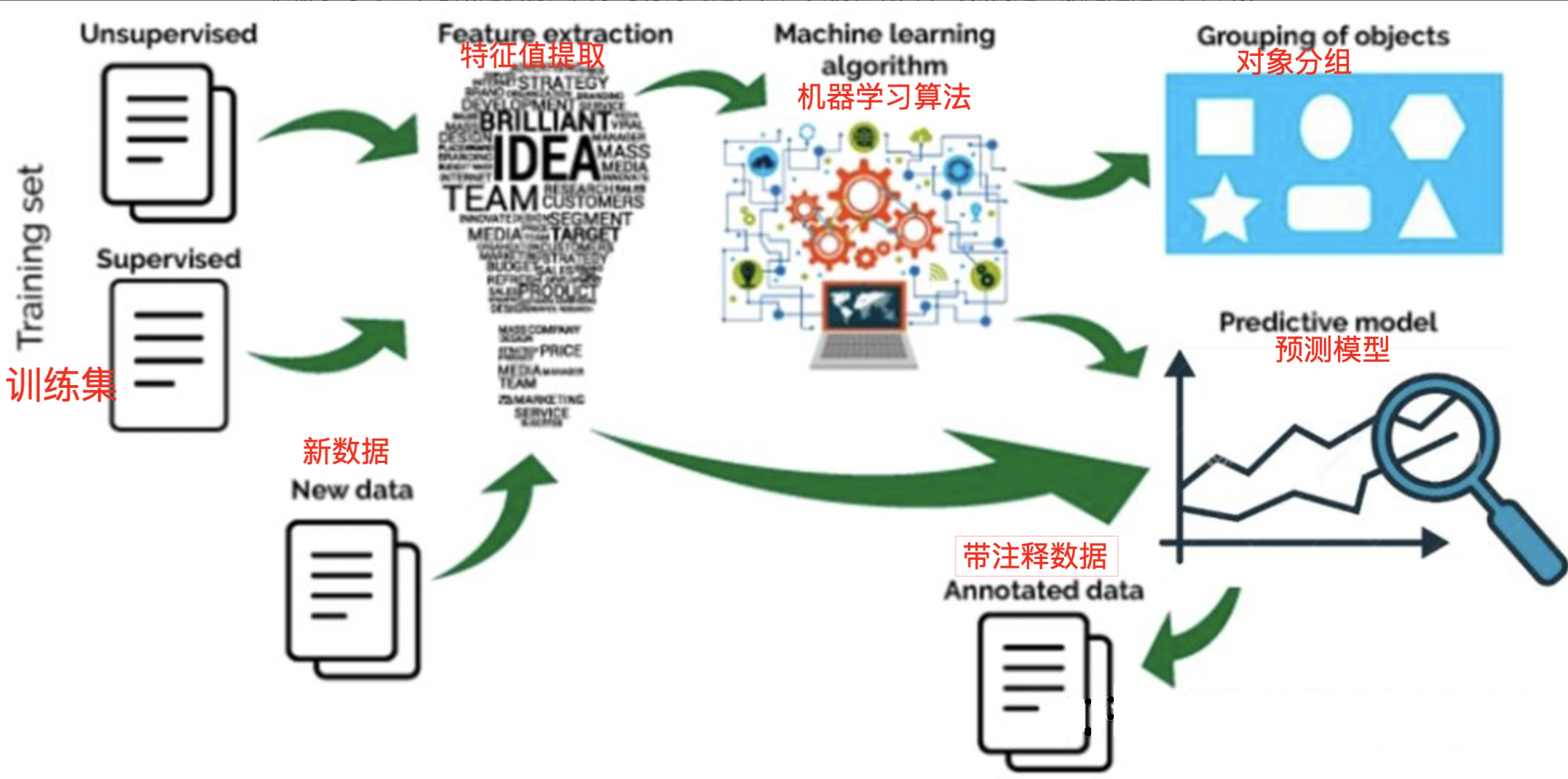
机器学习的本质是 "从数据中学习":
- 无需人类显式编写处理规则,而是通过算法从大量数据中挖掘潜在模式(如特征与结果的关联)。
- 随着数据量增加或训练迭代,模型性能会逐渐优化("学习" 过程)。
机械学习分类
根据数据是否包含 "标签"(即是否有明确的输出结果),机器学习可分为以下几类:
1. 监督学习
- 特点:训练数据包含 "输入特征" 和对应的 "标签(输出结果)",模型通过学习特征与标签的映射关系,实现对新数据的预测。
- 典型任务
- 分类(Classification):预测离散标签(如 "垃圾邮件 / 正常邮件""肿瘤良性 / 恶性")。
- 回归(Regression):预测连续数值(如房价、气温、股票价格)。
- 常见算法:线性回归、逻辑回归、决策树、随机森林、支持向量机(SVM)、神经网络等。
2. 半监督学习
- 特点:训练数据中只有少量标签,大部分为无标签数据,模型结合两种数据进行学习(适用于标签获取成本高的场景,如医学影像标注)。
- 典型应用:文本分类(少量标注文本 + 大量未标注文本训练模型)。
3. 无监督学习
- 特点:训练数据只有 "输入特征",无标签,模型需自主发现数据中的隐藏结构(如聚类、分布规律)。
- 典型任务
- 聚类(Clustering):将相似数据分组(如用户分群、商品分类)。
- 降维(Dimensionality Reduction):简化数据维度(如将高维图像特征压缩为低维向量,便于可视化或计算)。
- 异常检测(Anomaly Detection):识别与多数数据差异显著的样本(如信用卡欺诈检测)。
- 常见算法:K-Means 聚类、层次聚类、主成分分析(PCA)、t-SNE(降维可视化)等。
4. 强化学习
- 特点:模型通过与环境的 "交互" 学习:智能体(Agent)在环境中执行动作,根据动作结果获得 "奖励" 或 "惩罚",最终学习出最大化累积奖励的策略。
- 典型任务:游戏 AI(如 AlphaGo 下棋)、机器人控制(如自动驾驶避障)、资源调度等。
- 常见算法:Q-Learning、策略梯度(Policy Gradient)、深度强化学习(如 DQN)等。
机械学习的项目开发步骤
1.数据集的收集与获取:
- 确定数据来源:从数据库、API、文件或第三方获取数据。
- 数据采集:编写脚本或使用工具(如 Scrapy、Pandas)收集数据。
- 数据标注:如果是监督学习,需标注训练数据(如人工标注图像分类标签)。
2.数据预处理:
- 特征工程
- 特征提取:从原始数据中提取有用特征(如文本分词、图像特征提取)。
- 特征转换:标准化 / 归一化数值特征,编码分类特征。
- 特征选择:筛选对目标变量最有预测力的特征。
- 数据集划分:将数据分为训练集、验证集和测试集
3.模型选择与训练
以模型的形式选择适当的算法和数据表示
清理后的数据分为两部分 - 训练和测试。第一部分(训练数据)用于开发模型。第二部分(测试数据)用作参考依据。
4.模型评估与优化
使用验证集评估模型性能,选择合适的评估指标
scikit-learn
Scikit-learn(简称 sklearn)是 Python 中最流行的开源机器学习库之一,提供了丰富的工具和算法,用于数据预处理、模型选择、训练和评估。
Scikit-learn官网:https://scikit-learn.org/stable/#
1 scikit-learn安装
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple scikit-learn
2 sklearn数据集
1. sklearn 玩具数据集
无需额外下载:直接通过 sklearn 导入,方便快捷。
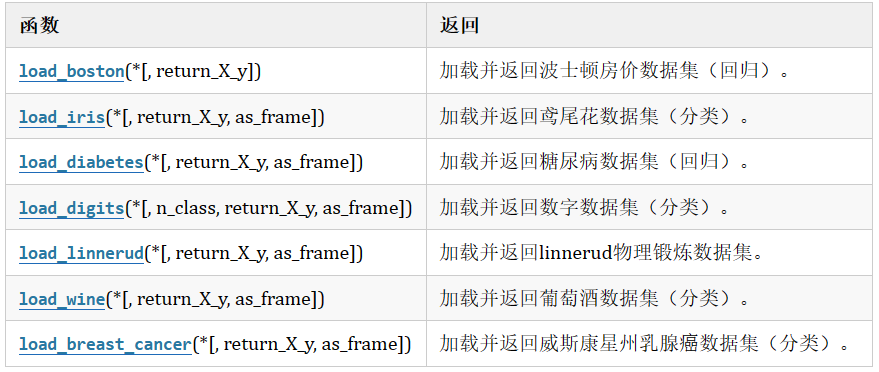
鸢尾花数据集
- 样本数:150 条。
- 特征数:4 个(花萼长度、花萼宽度、花瓣长度、花瓣宽度)。
py
from sklearn.datasets import load_iris
# 加载数据集
iris = load_iris()
print(iris)#--字典
print(iris.data)#数据每一朵花的特征值(特点数据,特征数据)
print(iris.feature_names)#特征名称:萼片长、萼片宽、花瓣长、花瓣宽
print(iris.target)#每朵花的标签:0、1、2
print(iris.target_names)#标签名称:山鸢尾、变色鸢尾、维吉尼亚鸢尾糖尿病数据集
- 样本数:442 条。
- 特征数:10 个
- 特征含义
- 年龄
- 性别
- 体质指数(BMI)
- 平均血压
- S1~S6:血液中 6 种血清指标
- 目标变量
- 一年后糖尿病病情进展的定量测量值(数值越大表示病情越严重)
py
from sklearn.datasets import load_diabetes
# 获取数据集
diabetes = load_diabetes()
# 查看数据集
# print(diabetes)
#特征值 和 目标值
x,y = load_diabetes(return_X_y=True)
# print(x,y)
print(x.shape,y.shape)#(442, 10) (442,)
print("特征名称:", diabetes.feature_names)
#['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']葡萄酒数据集
- 样本数:178 个
- 特征数:13 个(均为连续型数值特征)
- 特征含义
- 酒精含量
- 苹果酸含量
- 灰分
- 灰分碱度
- 镁含量
- 总酚含量
- 黄酮类化合物含量
- 非黄酮类酚含量
- 原花青素含量
- 颜色强度
- 色调
- 稀释葡萄酒的 OD280/OD315 值
- 脯氨酸含量
- 目标变量
- 葡萄酒的三个类别
- class_0 有 59 个样本,class_1 有 71 个样本,class_2 有 48 个样本
py
from sklearn.datasets import load_wine
# 获取数据集
wine = load_wine()
# 查看数据集
print(wine)
#特征值 和 目标值
x,y = load_wine(return_X_y=True)
# print(x,y)
print(x.shape,y.shape)#(178, 13) (178,)
print("特征名称:", wine.feature_names)
#['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines', 'proline']
print("类别名称:", wine.target_names)
#['class_0' 'class_1' 'class_2']2. sklearn现实世界数据集
使用 fetch_* 函数下载更大的现实世界数据集,这些数据需要联网获取并存储在本地。

20 新闻组数据集
- 任务类型:文本分类(20 个主题)。
- 样本数:约 20,000 条新闻文章。
- 特征数:文本特征(需通过 TF-IDF 等方法转换)。
py
from sklearn.datasets import fetch_20newsgroups
from sklearn import datasets
download_file_path = datasets.get_data_home()
print(datasets.get_data_home())
# 获取20newsgroups数据集
news_data = fetch_20newsgroups(data_home='../src',subset='all')
print(news_data.data[0])3. 数据集的划分
scikit-learn 中,将数据集划分为训练集(Training Set)和测试集(Test Set)
**sklearn.model_selection.train_test_split(*arrays,**options)
- array 这里用于接收1到多个"列表、numpy数组、稀疏矩阵或padas中的DataFrame"。
- 参数
- test_size 值为0.0到1.0的小数,表示划分后测试集占的比例
- random_state 随机种子,确保结果可复现。
- strxxxx 分层划分,填y
- shuffle:是否在划分前打乱数据(默认为 True)。
最常用的方法,随机将数据集划分为训练集和测试集。
python
from sklearn.model_selection import train_test_split
a=[10,20,30,40,50,60,70,80,90,100]
a_train , a_test = train_test_split(a)
# print(a_train,a_test)
#[10, 40, 70, 20, 30, 90, 50] [80, 100, 60]
python
a=[10,20,30,40,50,60,70,80,90,100]
b=[1,2,3,4,5,6,7,8,9,10]
#指定训练集和测试集的比例
# a_train , a_test , b_train , b_test = train_test_split(a,b,train_size=5)
# 随机种子
a_train , a_test , b_train , b_test = train_test_split(a,b,train_size=0.8,random_state=42)
print(a_train,a_test,b_train,b_test)特征工程
-
实例化转换器对象,转换器类有很多,都是Transformer的子类, 常用的子类有:
pyDictVectorizer 字典特征提取 CountVectorizer 文本特征提取 TfidfVectorizer TF-IDF文本特征词的重要程度特征提取 MinMaxScaler 归一化 StandardScaler 标准化 VarianceThreshold 底方差过滤降维 PCA 主成分分析降维 -
转换器对象调用fit_transform()进行转换, 其中fit用于计算数据,transform进行最终转换
fit_transform()可以使用fit()和transform()代替
pydata_new = transfer.fit_transform(data) 可写成 transfer.fit(data) data_new = transfer.transform(data)
1 DictVectorizer - 字典列表特征提取
将字典格式的数据(如 JSON)转换为数值特征矩阵,特别适合处理混合类型(数值 + 分类)的特征。
创建转换器对象:
sklearn.feature_extraction.DictVectorizer(sparse=True)
参数:
-
sparse=True返回类型为csr_matrix的稀疏矩阵
-
sparse=False表示返回的是数组,数组可以调用.toarray()方法将稀疏矩阵转换为数组
转换器对象:
转换器对象调用**fit_transform(data)**函数,参数data为一维字典数组或一维字典列表,返回转化后的矩阵或数组
转换器对象get_feature_names_out()方法获取特征名
示例1\] 提取为稀疏矩阵对应的数组
```python
from sklearn.feature_extraction import DictVectorizer
data = [
{
'city': '北京',
'temperature': 100,
'weather': '晴',
'wind': '微风',
'humidity': 80,
},
{
'city': '上海',
'temperature': 80,
'weather': '阴',
'wind': '小风',
'humidity': 60
},
{
'city': '广州',
'temperature': 70,
'weather': '雨',
'wind': '强风',
'humidity': 40
}
]
#模型研究x与y的关系前 必须保证xy中全是数字
#创建转换器
#spare = False 输出结果为矩阵
transfer = DictVectorizer(sparse = False)
data = transfer.fit_transform(data)
print(data)
# 查看转换后数据的特征名称
print(transfer.get_feature_names_out())
```
```py
[[ 0. 1. 0. 80. 100. 1. 0. 0. 0. 0. 1.]
[ 1. 0. 0. 60. 80. 0. 1. 0. 1. 0. 0.]
[ 0. 0. 1. 40. 70. 0. 0. 1. 0. 1. 0.]]
['city=上海' 'city=北京' 'city=广州' 'humidity' 'temperature' 'weather=晴'
'weather=阴' 'weather=雨' 'wind=小风' 'wind=强风' 'wind=微风']
```
\[示例2 \]提取为稀疏矩阵
```python
from sklearn.feature_extraction import DictVectorizer
data = [
{
'city': '北京',
'temperature': 100,
'weather': '晴',
'wind': '微风',
'humidity': 80,
},
{
'city': '上海',
'temperature': 80,
'weather': '阴',
'wind': '小风',
'humidity': 60
},
{
'city': '广州',
'temperature': 70,
'weather': '雨',
'wind': '强风',
'humidity': 40
}
]
#模型研究x与y的关系前 必须保证xy中全是数字
#创建转换器
#sparse = True 返回一个三元组表对象--稀松矩阵
transfer = DictVectorizer(sparse = True)
data = transfer.fit_transform(data)
print(data)
# 查看转换后数据的特征名称
print(transfer.get_feature_names_out())
# 稀松矩阵转换为数组
print(data.toarray())
```
则输出为
```py
ρ = 1:完全正线性相关;ρ = -1:完全负线性相关;ρ = 0:无线性相关(但可能存在非线性相关)。
对于两组数据 𝑋={𝑥1,𝑥2,...,𝑥𝑛} 和 𝑌={𝑦1,𝑦2,...,𝑦𝑛},皮尔逊相关系数可以用以下公式计算:
ρ = Cos ( x , y ) D x ⋅ D y = E [ ( x − E x ) ( y − E y ) ] D x ⋅ D y = ∑ i = 1 n ( x − x ~ ) ( y − y ˉ ) / ( n − 1 ) ∑ i = 1 n ( x − x ˉ ) 2 / ( n − 1 ) ⋅ ∑ i = 1 n ( y − y ˉ ) 2 / ( n − 1 ) \rho=\frac{\operatorname{Cos}(x, y)}{\sqrt{D x} \cdot \sqrt{D y}}=\frac{E[(x_-E x)(y-E y)]}{\sqrt{D x} \cdot \sqrt{D y}}=\frac{\sum_{i=1}^{n}(x-\tilde{x})(y-\bar{y}) /(n-1)}{\sqrt{\sum_{i=1}^{n}(x-\bar{x})^{2} /(n-1)} \cdot \sqrt{\sum_{i=1}^{n}(y-\bar{y})^{2} /(n-1)}} ρ=Dx ⋅Dy Cos(x,y)=Dx ⋅Dy E[(x−Ex)(y−Ey)]=∑i=1n(x−xˉ)2/(n−1) ⋅∑i=1n(y−yˉ)2/(n−1) ∑i=1n(x−x~)(y−yˉ)/(n−1)
|ρ|<0.4为低度相关; 0.4<=|ρ|<0.7为显著相关; 0.7<=|ρ|<1为高度相关
python
from scipy.stats import pearsonr
r1 = pearsonr(x,y)
py
from scipy.stats import pearsonr
x=[5,6,7,2,1,5,12,9,0,4]
y=[2,4,5,4,5,8,9,0,1,3]
p = pearsonr(x,y)
print(p)PearsonRResult(statistic=np.float64(0.3504442861308587), pvalue=np.float64(0.32081529829352373))2 主成分分析(PCA)
PCA的核心目标是从原始特征空间中找到一个新的坐标系统,使得数据在新坐标轴上的投影能够最大程度地保留数据的方差,同时减少数据的维度。
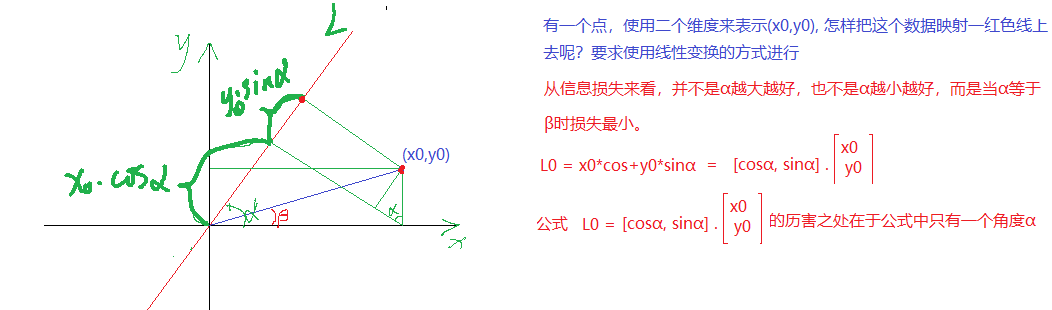
- 中心化数据:每个特征减去其均值
- 计算协方差矩阵:衡量特征间的相关性
- 特征值分解:计算协方差矩阵的特征值和特征向量
- 选择主成分:根据主成分的方差等,确定最终保留的主成分个数, 方差大的要留下;若一个特征的多个样本的值都相同,则方差为0,说明该特征值不能区分样本
- 投影数据:将原始数据投影到选定的特征向量上
from sklearn.decomposition import PCA
- PCA(n_components=None)
- 主成分分析
- n_components:
- 实参为小数时:表示降维后保留百分之多少的信息
- 实参为整数时:表示减少到多少特征
py
from sklearn.decomposition import PCA
import numpy as np
data = np.array([[2,8,4,5],
[6,3,0,8],
[5,4,9,1]])
pca = PCA(n_components=2)
data_new = pca.fit_transform(data)
print(data_new)[[-1.28620952e-15 3.82970843e+00]
[-5.74456265e+00 -1.91485422e+00]
[ 5.74456265e+00 -1.91485422e+00]]
py
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
iris = load_iris()
x=iris.data
y=iris.target
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=22)
transfer = PCA(n_components=2)
x_train = transfer.fit_transform(x_train)
#训练模型
#用模型预测
x_test = transfer.transform(x_test)
print(x_test)[[-2.36170948 0.64237919]
[ 2.05485818 0.16275091]
[ 1.23887735 0.10868042]
...
[ 0.3864534 -0.37888638]
[ 1.57303541 -0.53629936]
[-2.73553694 -0.15148737]
[ 2.53493848 0.51260491]
[ 1.91514709 0.1205521 ]
[ 2.42377809 0.38254852]
[ 1.41198549 -0.14338675]]