力扣经典算法篇-41-旋转图像(辅助数组法，原地旋转法）

1、题干

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1：

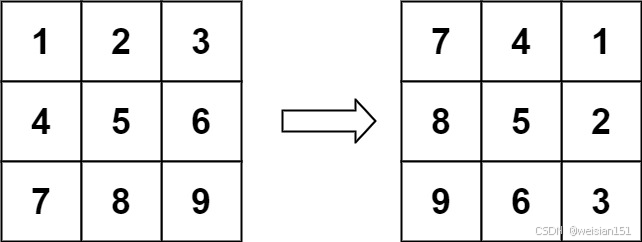
输入：matrix = $\[1,2,3$ , $4,5,6$ , $7,8,9$ ]

输出： $\[7,4,1$ , $8,5,2$ , $9,6,3$ ]

示例 2：

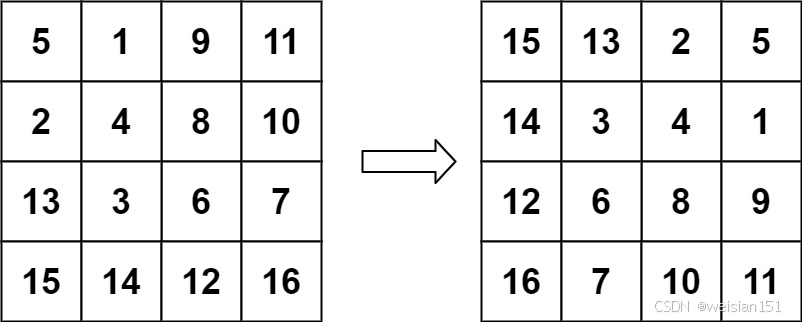
输入：matrix = $\[5,1,9,11$ , $2,4,8,10$ , $13,3,6,7$ , $15,14,12,16$ ]

输出： $\[15,13,2,5$ , $14,3,4,1$ , $12,6,8,9$ , $16,7,10,11$ ]

提示：

n == matrix.length == matrix $i$ .length

1 <= n <= 20

-1000 <= matrix $i$ $j$ <= 1000

2、解题

旋转数组，我们根据示例可以发现：原本的第一行数据旋转变成了最后一列；第二行的数据变成了倒数第二列；依次类推。

结合具体的数组找规律可以发现：

假设n=4，规律：3,0-->0,0 2,0-->0,1 1,0-->0,2 0,0-->0,3

从索引的角度可以发现：前元素的行=新元素的列；新元素的列+前元素的行=n-1

方法一：（辅助数组法）

使用辅助数组，保持和原数组相同的数据。可以借助辅助数组对原始数组快速赋值。
规律：

旋转后元素的行为之前的列；旋转后元素的列+之前的行=n-1

技巧：

需要结合当n=3和n=4的简单场景下，自己找规律，不能懒。

代码示例：

java 复制代码

import java.util.Arrays;

public class Test47 {

    // 使用辅助数组
    public static void rotate(int[][] matrix) {
        int n = matrix.length;
        int[][] matrixN = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                matrixN[i][j] = matrix[i][j];  // 辅助数组保持相同的数据
            }
        }

        // 假设=4，规律：3,0-0,0  2,0-0,1  1,0-0,2  0,0-0,3
        // 前元素的行=新元素的列；  新元素的列+前元素的行=n-1
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                matrix[i][j] = matrixN[n-j-1][i];    // 旋转后元素的行为之前的列；旋转后元素的列+之前的行=n-1
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
        rotate(matrix);
        System.out.println(Arrays.deepToString(matrix));
    }
}

方法二：（原地旋转法）

相对辅助数组法，原地选择法进需要一次遍历原始数据，且辅助空间为O(1)，性能更好，但是相对难度也高一点。

注意点：
（1）、一次旋转的规律

结合简单数据可以看出。下标位置变化如：（0,0）-->(0,5)-->(5,5)-->(5,0)-->(0,0)

可以发现相邻的两个数之间的内部一定相等，外部相加一定=n-1。

（2）、旋转的次数

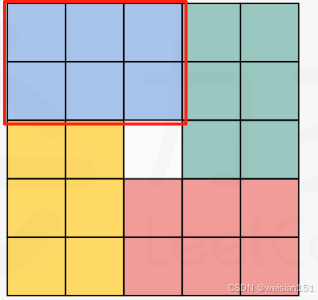
同一个元素会携带者对应的其他三个元素在一次过程中完成选择。所以不能完全遍历数据，会造成同一个元素多次旋转，最终回到原始数据。

如原始为一个55的二维数组，我们只需要对如下的2 3的区域进行旋转即可（或3*2的区域也一样）。如果旋转多了就会造成问题。

代码示例：

java 复制代码

import java.util.Arrays;

public class Test47 {

    public static void rotate(int[][] matrix) {
        int n = matrix.length;
        // 假设=4，规律：3,0-0,0  2,0-0,1  1,0-0,2  0,0-0,3
        // 前元素的行=新元素的列；  新元素的列+前元素的行=n-1
        for (int i = 0; i < (n + 1) / 2; i++) {    // 防止重复旋转（旋转一半，只能+1一次，横+1则纵不能+1）
            for (int j = 0; j < n / 2; j++) {      // 防止重复旋转
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];     // 规律：外部相等，内部相加=n-1
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
        rotate(matrix);
        System.out.println(Arrays.deepToString(matrix));
    }
}

向阳前行，Dare To Be！！！