基础知识
二叉树类型:
- 满二叉树:节点有两个子节点,且每一层都填满
- 完全二叉树:左顺序二叉树,每一层节点从最左节点依次开始
- 二叉搜索树:有序二叉树,节点的左子树节点<节点值<节点的右子树节点
- 平衡二叉搜索树:二叉搜索树+平衡(左右子树高度差<=1)
**存储方式:**链表/数组
遍历方式:
深度优先遍历DFS(递归法,迭代法):先往深处走,遇到空节点再往回走 数据结构:栈,先进后出(递归法,迭代法)
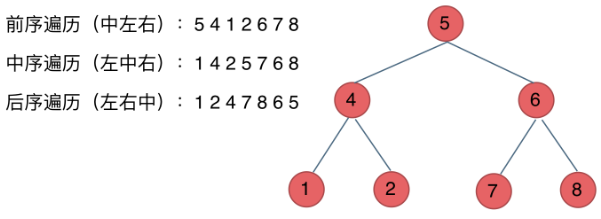
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中
观察:前中后,分别对应中的位置不同,其次一左一右;
广度优先遍历BFS(迭代法):一层一层遍历 数据结构:队列 先进先出
- 层次遍历
节点定义
java
class TreeNode{
int val;
TreeNode left,right;
TreeNode(){}
TreeNode(int val){this.val = val;}
TreeNode(int val,TreeNode left,TreeNode right){
this.val = val;
this.left = left;
this.right = right;
}
}算法思路:
- 确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
- 确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
- 确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
DFS
二叉树的前中后序遍历
java
public List<Integer> inorderTraversal(TreeNode root){
// 1.递归参数和返回值 入参 root 出参 res
List<Integer> res = new ArrayList<Integer>();
inorder(root,res);
return res;
}
public void inorder(TreeNode root,List<Integer> res){
// 2.终止条件 遇到节点
if(root == null){
return;
}
// 3.单层递归逻辑
res.add(root.val); // 前序遍历
inorder(root.left, res);
// res.add(root.val); // 中序遍历
inorder(root.right,res);
// res.add(root.val); // 后序遍历
}二叉树的最大深度
返还数值的一般都是全局单独定义
java
private int ans = 0;
public int maxDepth(TreeNode root){
// 1.递归的入参和出参
dfs(root,0);
return ans;
}
public void dfs(TreeNode root,int depth){
// 2.终止条件
if(root == null){
return;
}
// 3。单层递归逻辑
depth++;
ans = Math.max(ans,depth);
dfs(root.left,ans);
dfs(root.right,ans);
}翻转二叉树
java
public TreeNode invertTree(TreeNode root){
dfs(root);
return root;
}
public void dfs(TreeNode root){
if(root == null){
return;
}
// 节点互换
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
// 递归
dfs(root.left);
dfs(root.right);
}对称二叉树
java
public boolean isSymmetric(TreeNode root){
if(root == null){
return true;
}else {
return dfs(root.left,root.right);
}
}
public boolean dfs(TreeNode left,TreeNode right){
if(left == null && right == null){
return true;
}
if(left == null || right == null || left.val!=right.val){
return false;
}
return dfs(left.right,right.left) && dfs(left.left,right.right);
}二叉树直径
思路:
java
private int ans;
public int diameterOfBinaryTree(TreeNode root){
dfs(root);
return ans;
}
private int dfs(TreeNode root){
if(root == null){
return -1;
}
int leftLen = dfs(root.left)+1;
int rightLen = dfs(root.right)+1;
ans = Math.max(ans,leftLen+rightLen);
return Math.max(leftLen,rightLen);
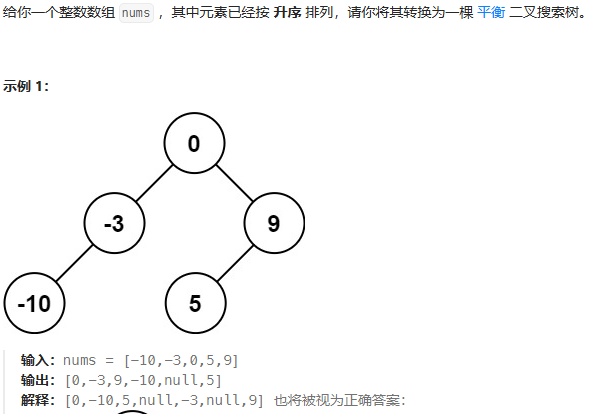
}有序数组转二叉搜索树(前序遍历)
思路:
java
public TreeNode sortedArrayToBST(int[] nums){
return dfs(nums,0,nums.length-1);
}
public TreeNode dfs(int[] nums,int left,int right){
if(left > right){
return null;
}
int mid = left+(right-left)/2;
TreeNode root = new TreeNode(nums[mid]);
root.left = dfs(nums,left,mid-1);
root.right = dfs(nums,mid+1,right);
return root;
}验证二叉搜索树
思路:
java
class Solution {
public boolean isValidBST(TreeNode root) {
return dfs(root, null, null); // 初始时无边界限制
}
private boolean dfs(TreeNode node, Integer min, Integer max) {
if (node == null) {
return true;
}
// 检查当前节点值是否在 (min, max) 范围内
if ((min != null && node.val <= min) || (max != null && node.val >= max)) {
return false;
}
// 递归检查左子树(最大值限制为当前节点值)
// 递归检查右子树(最小值限制为当前节点值)
return dfs(node.left, min, node.val) && dfs(node.right, node.val, max);
}
}二叉搜索树第k小的树
思路:将二叉树转化为数组,并对数组排序,遍历数组到k-1(从0索引)位置;
应该是利用搜索树特性
java
class Solution {
private int k;
public int kthSmallest(TreeNode root, int k) {
this.k = k;
return dfs(root);
}
private int dfs(TreeNode node){
if(node == null){
return -1;
}
int leftRes = dfs(node.left);
if(leftRes != -1){
return leftRes;
}
if(--k == 0){
return node.val;
}
return dfs(node.right);
}
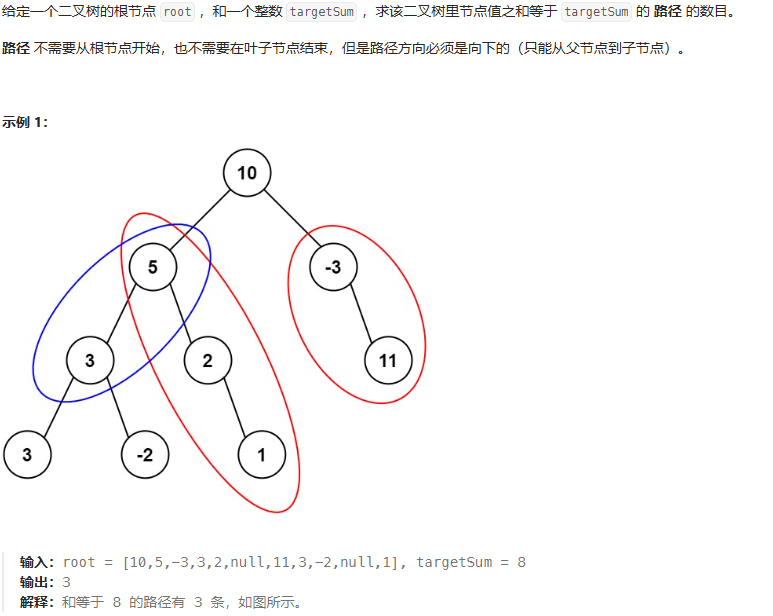
}路径和Ⅲ
思路:
java
class Solution {
public int pathSum(TreeNode root, long targetSum) {
if(root == null){
return 0;
}
int ret = rootSum(root,targetSum);
ret += pathSum(root.left, targetSum);
ret += pathSum(root.right, targetSum);
return ret;
}
public int rootSum(TreeNode root ,long targetSum){
int ret = 0;
if(root == null){
return 0;
}
int sum = root.val;
if(sum == targetSum){
ret++;
}
ret += rootSum(root.left, targetSum - sum);
ret += rootSum(root.right, targetSum - sum);
return ret;
}
}二叉树最近公共先祖
思路:

java
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return sfz(root, p, q);
}
public TreeNode sfz(TreeNode node,TreeNode p,TreeNode q){
if(node == null){
return null;
}
if(node.val == p.val || node.val == q.val){
return node;
}
TreeNode left = sfz(node.left,p,q);
TreeNode right = sfz(node.right,p,q);
if(left!=null&&right!=null){
return node;
}
return left !=null?left:right;
}
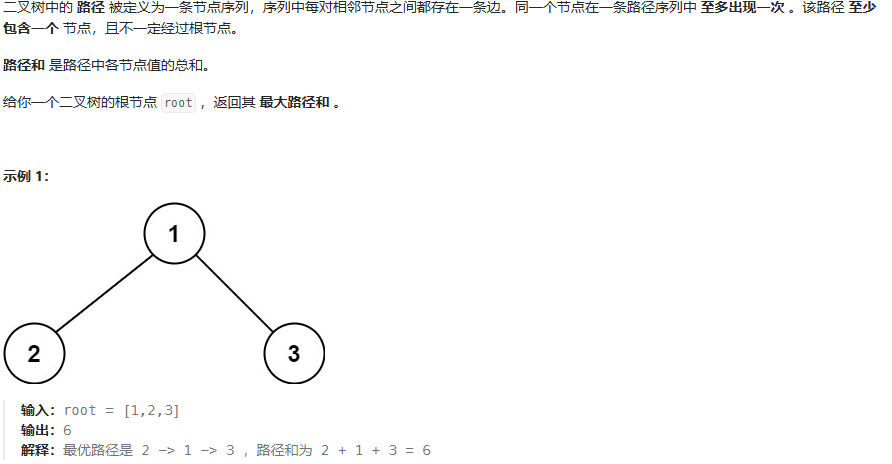
}二叉树最大路径和
思路:
java
class Solution {
public int maxPathSum(TreeNode root) {
int[] max = new int[1];
max[0] = Integer.MIN_VALUE;
getMaxSum(root,max);
return max[0];
}
public int getMaxSum(TreeNode root,int[] max){
if(root == null){
return 0;
}
int left = Math.max(0,getMaxSum(root.left,max));
int right = Math.max(0,getMaxSum(root.right,max));
int currentMax = root.val + left +right;
max[0] = Math.max(max[0],currentMax);
return root.val+Math.max(left,right);
}
}BFS
适用场景:「层序遍历」、「最短路径」
java
// 二叉树的层序遍历
void bfs(TreeNode root) {
Queue<TreeNode> queue = new ArrayDeque<>();
queue.add(root);
while (!queue.isEmpty()) {
int n = queue.size();
for (int i = 0; i < n; i++) {
// 变量 i 无实际意义,只是为了循环 n 次
TreeNode node = queue.poll();
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
}二叉树层序遍历
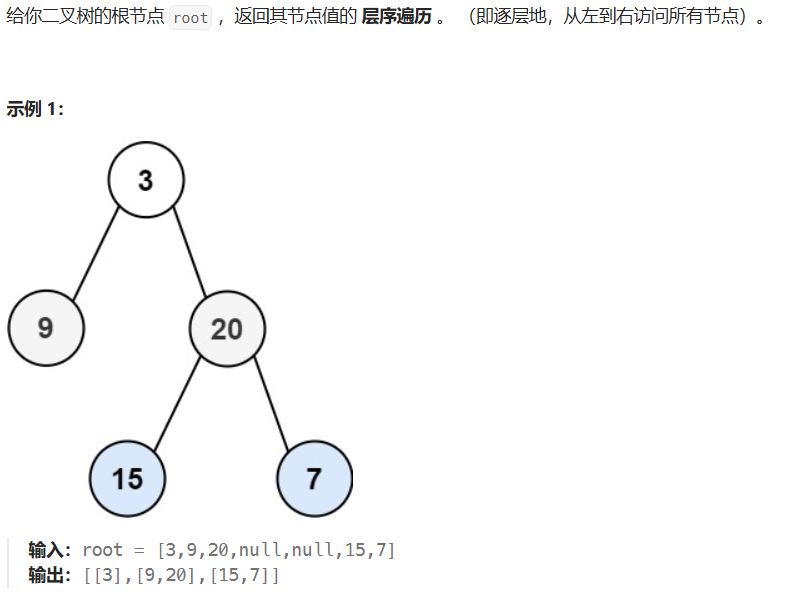
java
public List<List<Integer>> levelOrder(TreeNode root){
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if(root != null){
queue.add(root);
}
while (!queue.isEmpty()){
int n = queue.size();
List<Integer> level = new ArrayList<>();
for(int i =0;i<n;i++){
TreeNode node = queue.poll();
level.add(node.val);
if(node.left!=null){
queue.add(node.left);
}
if(node.right!=null){
queue.add(node.right);
}
}
res.add(level);
}
return res;
}