1. 什么是决策树
学过数据结构与算法的小伙伴应该对树不陌生吧,这里的决策树也是大同小异的,只是每次反之都有一个条件来决定流向的。
1.1 决策节点
通过条件判断而进行分支选择的节点。如:将某个样本中的属性值(特征值)与决策节点上的值进行比较,从而判断它的流向。
1.2 叶子节点
没有子节点的节点,表示最终的决策结果。
1.3 决策树的深度
所有节点的最大层次数。
决策树具有一定的层次结构,根节点的层次数定为0,从下面开始每一层子节点层次数增加
1.4 决策树优点:
可视化 - 可解释能力-对算力要求低
1.5 决策树缺点:
容易产生过拟合,所以不要把深度调整太大了。
2. 为什么有决策树这个算法
决策树的出现,本质上是为了模拟人类的结构化决策过程,并解决实际场景中 "如何从数据中提炼规则" 的问题。具体原因可从以下角度理解:
2.1 模拟人类决策逻辑
人类在做决策时,往往会通过一系列 "是非判断" 逐步缩小范围。例如:买水果时,先看 "是否成熟"→ 再看 "价格是否合理"→ 最后决定 "买不买";医生诊断时,先问 "是否发烧"→ 再查 "是否咳嗽"→ 最后判断 "可能的疾病"。决策树正是将这种 "层层判断" 的逻辑转化为数学模型,用树状结构(根节点→内部节点→叶节点)清晰呈现决策步骤,让机器能像人一样 "有条理地思考"。
2.2 解决 "从数据到规则" 的转化问题
现实中,很多数据隐含着可解释的决策规则(比如 "什么样的用户会流失""哪些贷款申请有风险"),但这些规则往往混杂在大量数据中,难以直接观察。
决策树通过算法自动从数据中挖掘这些规则(例如 "如果用户月消费>500 元且使用时长>2 年,则流失概率低"),并以树状图的形式可视化,让规则变得可理解、可复用。
2.3 应对复杂场景的灵活性
与早期的简单模型(如线性回归)相比,决策树能处理非线性关系(例如 "年龄对购买意愿的影响不是简单的正比或反比"),也能同时处理数值型数据(如收入)和类别型数据(如性别),适用场景更广泛。
举个例子

我们的决策树深度越深是不是就分的越详细,然后就越正确,但是这样往往就会过度拟合了,我们前面介绍到决策树算力较低那这个地方体现在哪里,看上面的例子,左边和右边的起始条件不同,所以分类的过程也是不一样的,但是我的起始条件对分类越重要是不是就能越快得出结果,那我们怎么来确定这个特征的重要程度呢?
3. 基于信息增益决策树的建立
3.1 信息熵
熵这个词出现在热力学中,熵越大,说明事物越混乱,越不确定,在机器学习中,特征越是不确定是不是就越难确定最终的分类结果,这种不确定性在这里成为信息熵,熵的大小取决于 "不同取值的概率分布是否均匀",比如
用 "身高" 预测 "是否喜欢吃辣"。假设身高 160cm 的人中,50% 喜欢吃辣、50% 不喜欢;身高 170cm 的人中,同样是 50% 喜欢、50% 不喜欢...... 无论身高取什么值,目标类别的分布都接近均匀。此时 "身高" 的不确定性高(熵大),但身高数据本身是准确测量的(比如用卷尺精确记录),只是它和 "是否喜欢吃辣" 无关。
3.2 信息商的公式

3.3 信息增益
信息增益是一个统计量,用来描述一个属性区分数据样本的能力。信息增益越大,那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量, 上面的例子就有信息增益的影子,信息增益公式:
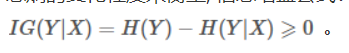
信息增益越大的是不是越能反映和类别的关联程度,所以越大的特征就放到前面的决策点出。
3.4 信息增益决策树建立步骤
我们先来算一下信息增益,
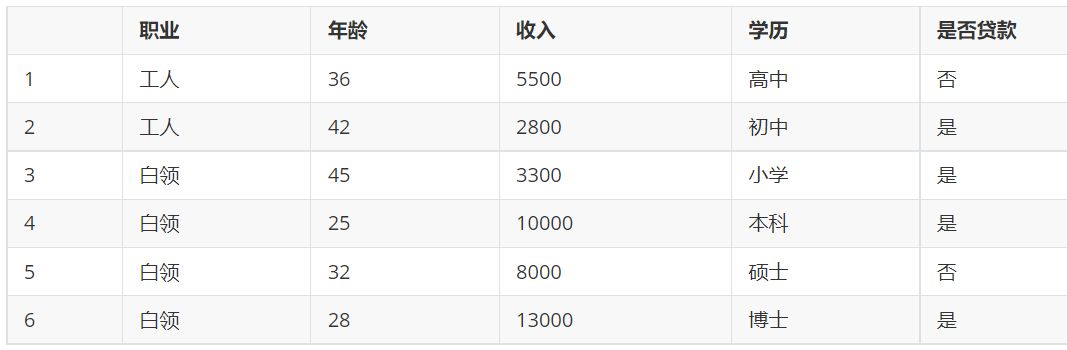
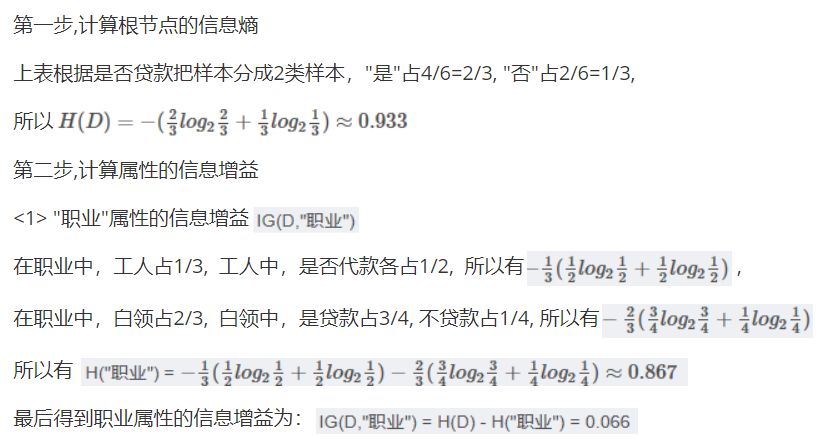
但是这里我们算的是职业他的类别很少,我们可以有具体得分类,要是我们看年龄的信息增益且不是要分好多次,所以我们这里以35为界限,弄一个范围,假如我们每一个值都归为一类虽然算力大,但是确实很准的,我们可不能要很准的结果。

假如就是职业算的信息增益最大,那我们就把他放到第一个判断的决策点,然后我们将这个特征筛选出,对剩下的重新计算,算出新的最大的信息增益。
4 基于基尼指数决策树的建立(了解)
基尼指数(Gini Index)是决策树算法中用于评估数据集纯度的一种度量,基尼指数衡量的是数据集的不纯度,或者说分类的不确定性。在构建决策树时,基尼指数被用来决定如何对数据集进行最优划分,以减少不纯度。
基尼指数的计算
对于一个二分类问题,如果一个节点包含的样本属于正类的概率是 (p),则属于负类的概率是 (1-p)。那么,这个节点的基尼指数 (Gini(p)) 定义为:

基尼指数的意义
-
当一个节点的所有样本都属于同一类别时,基尼指数为 0,表示纯度最高。
-
当一个节点的样本均匀分布在所有类别时,基尼指数最大,表示纯度最低。
基尼指数越小的,越排到前面,确定了第一个之后,后面的也继续重复操作。
5 api
class sklearn.tree.DecisionTreeClassifier(....)
参数:
criterion "gini" "entropy" 默认为="gini"
当criterion取值为"gini"时采用 基尼不纯度(Gini impurity)算法构造决策树,
当criterion取值为"entropy"时采用信息增益( information gain)算法构造决策树.
max_depth int, 默认为=None 树的最大深度
可视化决策树
function sklearn.tree.export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)
参数:
estimator决策树预估器
out_file生成的文档
feature_names节点特征属性名
功能:
把生成的文档打开,复制出内容粘贴到"http://webgraphviz.com/"中,点击"generate Graph"会生成一个树型的决策树图
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier, export_graphviz
# 1)获取数据集
iris = load_iris()
# 2)划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
#3)标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4)决策树预估器
estimator = DecisionTreeClassifier(criterion="entropy")
estimator.fit(x_train, y_train)
# 5)模型评估,计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
# 6)预测
index=estimator.predict([[2,2,3,1]])
print("预测:\n",index,iris.target_names,iris.target_names[index])
# 可视化决策树
export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)