决策树技术详解：从理论到Python实战

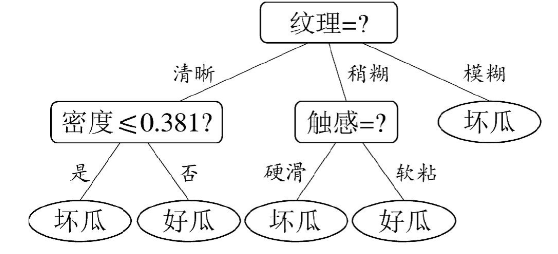
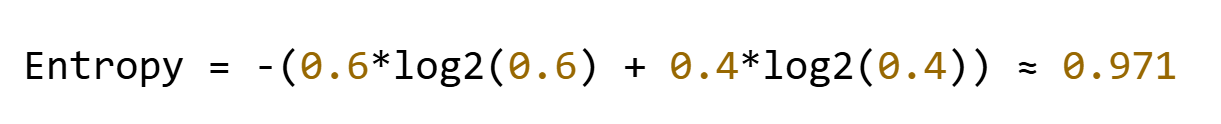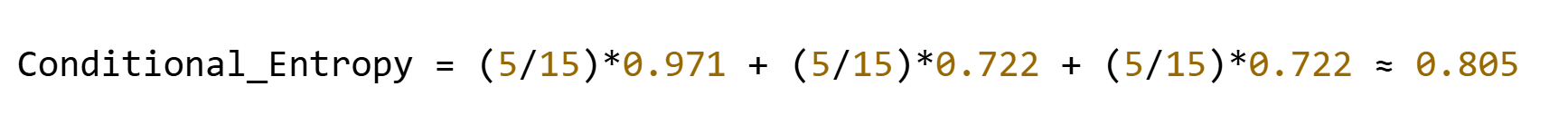​决策树像人类的思考过程，用一系列"是/否"问题层层逼近答案

​

一、决策树的核心本质

决策树是一种模仿人类决策过程 的树形结构分类/回归模型。它通过节点（问题） 和 边（答案）​ ​ 构建路径，最终在叶节点（决策结果） 输出预测值。这种白盒模型 的优势在于极高的可解释性。

---

二、决策树的核心构成

1. 根节点：初始特征划分点
2. 内部节点：特征测试点（每个节点对应一个判断条件）
3. 分支：判断条件的可能结果
4. 叶节点：最终决策结果（分类/回归值）

​关键概念​：

• 纯度（Purity）​ ：节点内样本类别的统一程度（Gini指数/熵越小越纯）
• 信息增益（Information Gain）​ ：分裂后纯度的提升量
• 剪枝（Pruning）​ ：防止过拟合的关键技术（预剪枝/后剪枝）

---

三、决策树的数学原理

决策树通过递归分割寻找最优特征：

1、​选择分裂特征​：

• ID3算法 ：使用信息增益（缺陷：偏好多值特征）
• C4.5算法 ：改进为增益率（消除特征取值数量的影响）
• CART算法 ：使用Gini指数 （计算效率更高） ------Classification and Regression Tree（分类和回归任务都可用）

---

​2、停止条件​：

• 节点样本全属同一类
• 特征已用完
• 样本数低于阈值（超参数控制）

---

四、算法对比

ID3算法概括

ID3（Iterative Dichotomiser 3）算法的计算过程可概括为：​通过递归地选择信息增益最大的特征进行节点分裂，最终构建决策树。具体步骤为：

1. 计算当前节点的信息熵
2. 对每个特征计算分裂后的信息增益（原始熵 - 条件熵）
3. 选择增益最大的特征作为分裂节点
4. 对子节点重复上述过程，直到满足停止条件

算法名称中的"ID3"来源于：

• Iterative（迭代）：通过循环过程构建树
• Dichotomiser（二分）：早期版本仅处理二分类（虽然后续支持多分类）
• 3：代表第三代改进版本

其核心思想是用信息论量化特征重要性，每次分裂都选择能最大程度降低系统不确定性的特征。

​**ID3算法：**信息增益（Information Gain）

信息增益是决策树（ID3算法）选择分裂特征的核心指标，它量化了使用某特征进行分割后，系统不确定性的减少程度。要彻底理解这个公式，我们需要分三步拆解：

---

1、信息熵（Entropy）

​信息熵 表示系统的混乱程度，计算公式为：

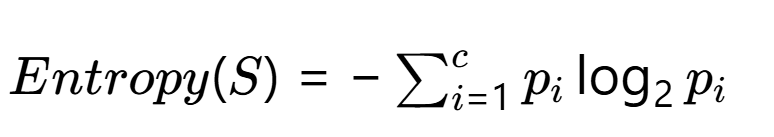
• S：当前节点的样本集合
• c：类别总数（如二分类时c=2）
• pi：样本中第i类所占比例

​示例​：假设某节点有10个样本，其中6个正例，4个负例：

---

2、条件熵（Conditional Entropy）

当按某个特征A分裂后，需要计算加权平均熵​：

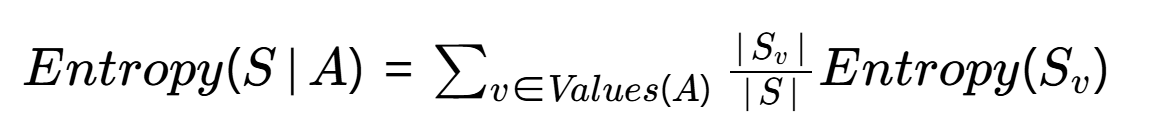
• Values(A)：特征A的取值集合（如"年龄"特征可能取{青年,中年,老年}）
• Sv：A取值为v的子集样本

​示例​：按特征"天气"（取值为晴/雨/阴）分裂：

• 晴：3正2负 → Entropy=0.971
• 雨：1正4负 → Entropy=0.722
• 阴：4正1负 → Entropy=0.722

---

3、信息增益计算公式

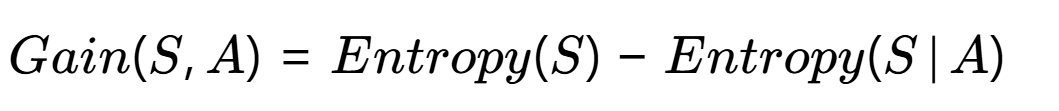
​物理意义 ​：原始系统的熵减去按特征A分裂后的条件熵

​接前例 ​：

若原数据集Entropy(S)=0.88，则：

---

4、计算实例演示

目标​：预测是否打球（二分类问题）

特征​：天气、温度、湿度、风力

4个样本​：

天气	温度	湿度	风力	打球
晴	高	高	弱	否
晴	高	高	强	否
阴	高	高	弱	是
雨	中	高	弱	是

​步骤1 ​**：计算原始熵**

公式 ​：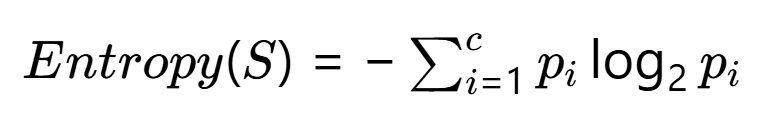

​计算过程​：

• 总样本数：4个
• 正例（"是"）：2个 → p₁ = 2/4 = 0.5
• 反例（"否"）：2个 → p₂ = 2/4 = 0.5

---

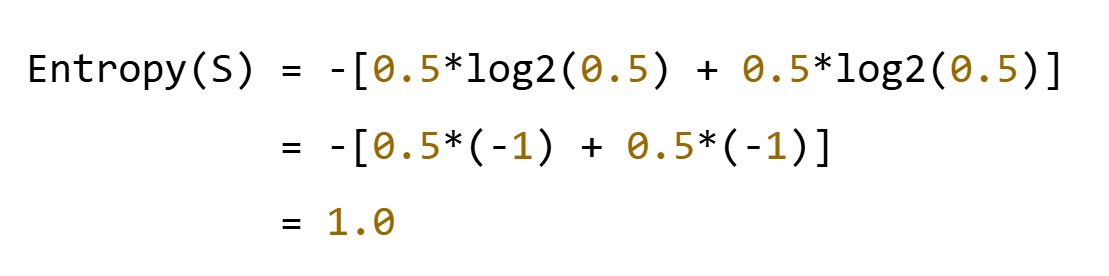
步骤2 ​：计算各特征的信息增益

1. 特征"天气"（3个取值：晴/阴/雨）

​子集划分​：

• 晴：2个（否, 否）→ Entropy = 0
• 阴：1个（是）→ Entropy = 0
• 雨：1个（是）→ Entropy = 0

​条件熵​：

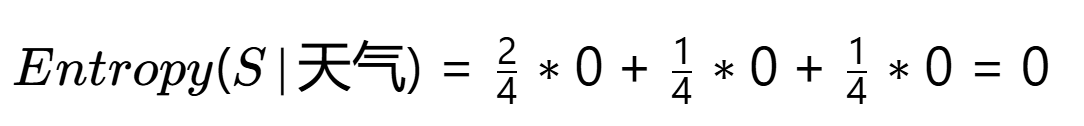
​信息增益​：Gain(天气)=1.0−0=1.0

---

2. 特征"温度"（2个取值：高/中）

​子集划分​：

• 高：3个（否, 否, 是）→ p(是)=1/3, p(否)=2/3

  Entropy = -[1/3*log2(1/3) + 2/3*log2(2/3)] ≈ 0.918

• 中：1个（是）→ Entropy = 0

​条件熵​：

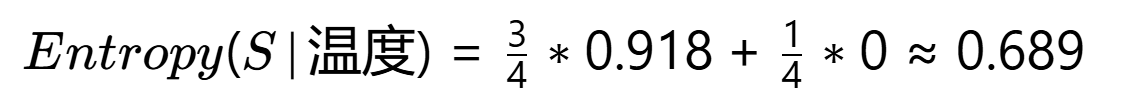
​信息增益​：Gain(温度)=1.0−0.689=0.311

---

3. 特征"湿度"（仅1个取值：高）

​子集划分​：

• 高：4个 → 与父节点相同

​信息增益​：Gain(湿度)=1.0−1.0=0

---

4. 特征"风力"（2个取值：弱/强）

​子集划分​：

• 弱：3个（否, 是, 是）→ p(是)=2/3, p(否)=1/3

  Entropy = -[2/3*log2(2/3) + 1/3*log2(1/3)] ≈ 0.918

• 强：1个（否）→ Entropy = 0

​条件熵​：

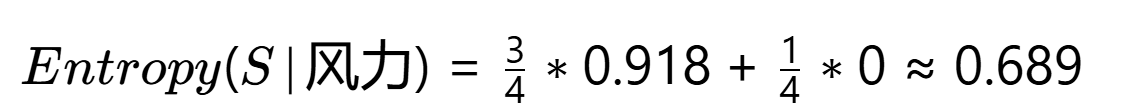
​信息增益​：Gain(风力)=1.0−0.689=0.311

---

​步骤3​：选择根节点

各特征增益比较​：

• 天气：1.0
• 温度：0.311
• 湿度：0
• 风力：0.311

​选择标准 ​：选择信息增益最大的特征 → ​决策 ​：选择"天气"作为根节点

---

步骤4：构建子树

分裂结果​：

天气
├─ 晴 → 全部为"否"（叶节点）
├─ 阴 → 全部为"是"（叶节点）
└─ 雨 → 全部为"是"（叶节点）

停止条件​：

• 所有分支的叶节点纯度已达100%
• 无需继续分裂

最终决策树

---

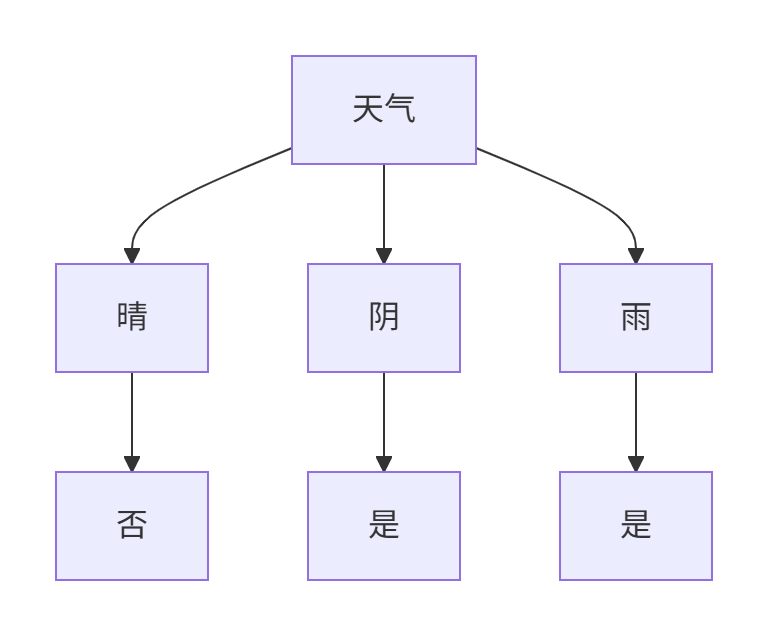
5、注意事项

1. ​偏向性问题 ​：当特征取值较多时（如"ID"特征），信息增益会倾向于选择该特征（导致过拟合），因此C4.5算法改用增益率。

2. ​对数底选择​：虽然理论上可使用任意底数，但机器学习中常用2为底（结果单位为bits）

3. ​与Gini指数的关系​：两者都衡量纯度，但Gini指数计算更快（无对数运算）：

   

---

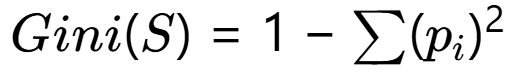
通过这种量化的方式，决策树可以自动选择最具区分力的特征进行分裂，这正是它模拟人类决策智能的核心所在。

---

C4.5算法：增益率（Gain Ratio）

​​"信息增益率是给信息增益装上刹车片，防止它冲向多值特征的悬崖"​​

1、为什么要改进信息增益？

信息增益（ID3算法）存在严重偏差​：它会优先选择取值数目多的特征（如"用户ID"这种唯一值特征），但这会导致：

1. 无效分裂：每个ID对应一个样本，Gain达到最大值但毫无预测能力
2. 过拟合风险：生成过于复杂的树结构

​示例​：在员工离职预测中：

• 特征A（部门）：5个取值 → Gain=0.3
• 特征B（员工ID）：1000个唯一值 → Gain=1.0
  ID3会错误地选择B作为根节点

2、增益率的数学本质

C4.5算法用增益率（Gain Ratio）​​ 修正这一问题，公式为：

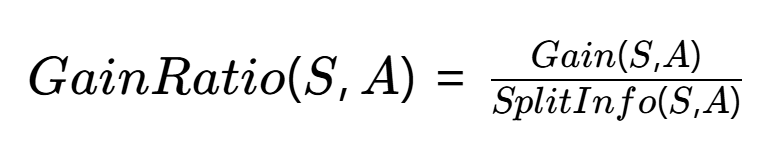
其中分裂信息（Split Information）：

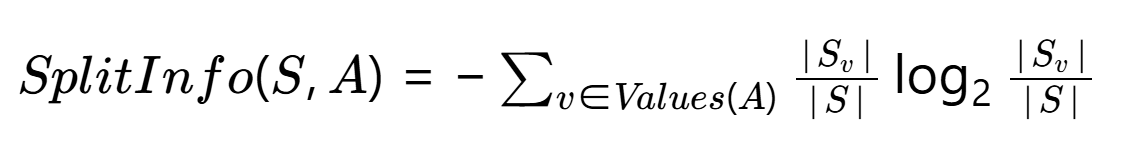
​关键点​：

• 分子：原始信息增益
• 分母：特征A本身的信息熵（惩罚多值特征）
• 当特征取值均匀分布时，SplitInfo达到最大值

想象你在水果摊挑西瓜，老板让你用最少的提问找出最甜的瓜。增益率就是帮你衡量"每个提问的价值"的智能计算器。

1️⃣ ​信息增益 = 提问带来的信息量​

• 你问："是红瓤吗？"（可能筛掉一半不甜的瓜）
• 信息增益就是这个问题帮你减少的不确定性

2️⃣ ​分裂信息 = 问题本身的复杂程度​

• 如果问："瓜的编号是多少？"（每个瓜编号唯一）
  • 这个问题太"细致"了，虽然能精准找瓜，但没实际意义
  • 分裂信息就会很大，表示问题本身太复杂

3️⃣ ​增益率 = 真正的有效信息量​

就像老板会提醒你：

• "问颜色"（增益率0.8）比"问编号"（增益率0.01）更划算
• "问产地"（增益率0.3）不如"问敲声"（增益率0.6）有效

增益率就是防止你被"假聪明问题"忽悠的计算器------有些问题看似能精确分类（比如问身份证号），实际上对挑西瓜毫无帮助。

---

3、计算实例分步演示

数据集：

天气	风速	打球
晴	弱	否
晴	强	否
阴	弱	是
雨	强	是
雨	弱	是
雨	强	否

---

第一步：计算原始信息熵

---

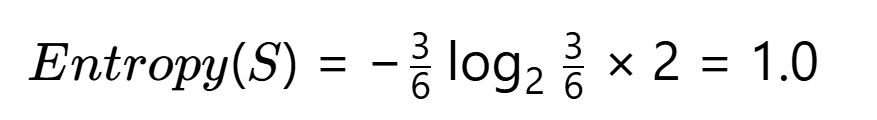
第二步：计算各特征信息增益

1. 特征"天气"（3个取值）

​子集划分​：

• 晴：2否 → Entropy=0
• 阴：1是 → Entropy=0
• 雨：2是1否 → Entropy=0.918

​条件熵​：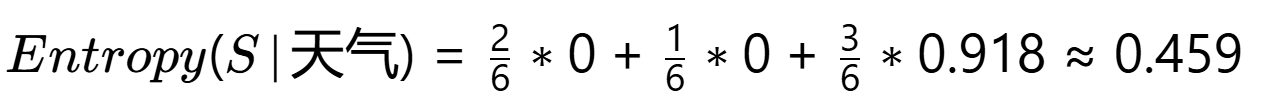

​信息增益​：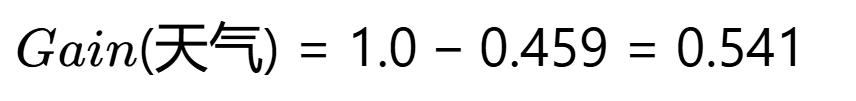

​分裂信息​：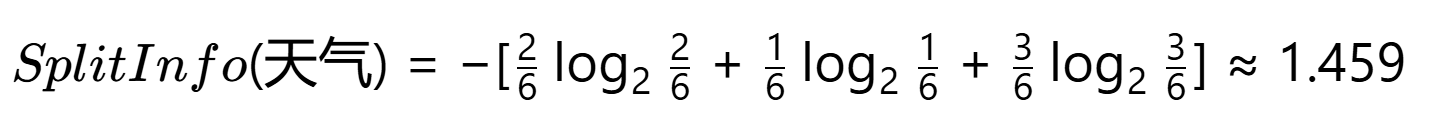

​增益率​：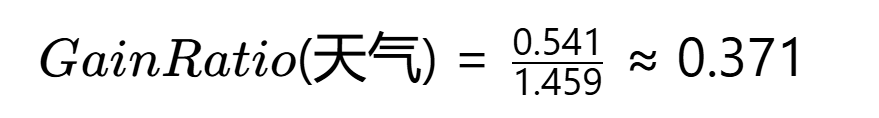

---

2. 特征"风速"（2个取值）

​子集划分​：

• 弱：1否2是 → Entropy=0.918
• 强：2否1是 → Entropy=0.918

​条件熵​：

​信息增益​：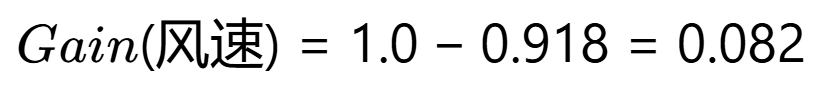

​分裂信息​：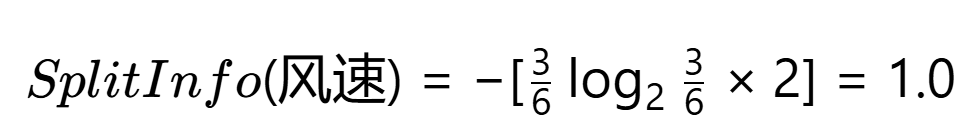

​增益率​：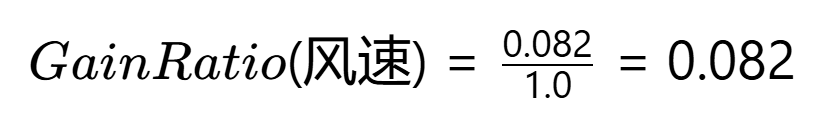

---

第三步：特征选择对比

特征	信息增益	增益率
天气	0.541	0.371
风速	0.082	0.082

​决策​：选择增益率更高的"天气"作为分裂节点

---

第四步：验证多值特征惩罚

假设新增无关特征"日期"（5个唯一值）：

​计算SplitInfo(日期)​​：

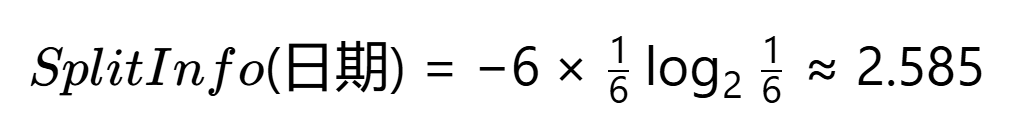
即使Gain(日期)=0.971（最大可能值）：

实际选择​：虽然"日期"增益率(0.387) > "天气"(0.371)，但：

1. 业务上排除无意义特征
2. 可设置增益率阈值（如>0.4）过滤伪特征

---

关键结论

1. 增益率机制 ：有效压制了"风速"等弱特征和"日期"等伪特征
2. 计算本质：用特征自身熵对信息增益进行标准化
3. 业务价值：选择天气（晴/阴/雨）作为首分裂特征，符合"恶劣天气不打球"的常识

---

4、C4.5的完整改进措施

（1）处理连续特征（解决数值型数据问题）

核心思想 ​：将"年龄"这类连续数字变成可分类的阈值点

​具体操作​：

1. 排序所有取值（如年龄[22, 25, 30]）
2. 计算相邻值中点（→23.5, 27.5）
3. 将这些中点作为候选分割阈值

​示例​：用年龄预测是否购买保险：

• 测试条件1：年龄≤23.5？
• 测试条件2：年龄≤27.5？
• 选择信息增益率最高的分割点

​业务意义​：自动找到关键年龄分界点（如27.5岁可能是消费习惯转变的临界值）

---

（2）处理缺失值（解决数据不完整问题）

核心思想 ​：按已知数据的比例"分配"缺失样本

​具体操作​：

1. 计算已知数据的类别分布（如A类60%，B类40%）
2. 将缺失样本按此比例分配到各分支

​示例 ​：

10个客户数据预测：

• 8个已知数据：5个A类（62.5%），3个B类（37.5%）
• 2个缺失数据：
  • 1.25个（≈1个）分到A类分支
  • 0.75个（≈1个）分到B类分支

---

**（3）后剪枝（解决过拟合问题）**​

核心思想 ​：先长完整棵树，再修剪掉不可靠分支

​具体操作​：

1. 用训练集生成完整决策树
2. 用验证集测试每个子树：
   • 如果替换为叶节点能提升验证集准确率
   • 则剪掉该子树

​示例​：某子树规则

温度>30?
├─ 是 → 湿度<50%? → 分类A
└─ 否 → 分类B

验证发现：

• 直接合并为"温度>30? → 分类A/分类B"准确率更高
• 则剪除"湿度"判断分支

三者的内在联系

1. 连续特征处理：扩展算法应用范围（数值型数据）
2. 缺失值处理：增强算法鲁棒性（现实数据总有缺失）
3. 后剪枝：提升模型泛化能力（防止记住噪声）

完整工作流图示​：

5、业务应用中的特殊处理

当遇到极端多值特征​（如城市名称）时：

1. 业务分组 ：将取值按业务逻辑合并（如一线/二线城市）
2. 统计合并 ：将低频取值合并为"其他"类别
3. 特征重要性筛选 ：先计算所有特征的增益率，人工剔除异常值

---

通过这种改进，C4.5算法实现了：

1. 抗多值干扰：避免选择无意义的细分特征
2. 更好的泛化性：生成的决策规则更具普适性
3. 业务可解释性：分裂特征更符合业务逻辑

这种思想也深刻影响了后续的机器学习算法设计------任何纯粹的统计指标都需要考虑其潜在的分布偏差。

---

CART算法：Gini指数

​​"Gini指数像一把快刀，用最简单的计算实现最有效的分割"​​

1、CART算法的核心特点

Classification and Regression Trees (CART) 是决策树家族的里程碑算法，其独特之处在于：

1. 二叉树结构 ：每个节点只做二元分裂（即使特征有多个取值）
2. 万能性 ：唯一能同时处理分类（Gini指数） 和回归（方差最小化）的树算法
3. 高效率 ：Gini指数计算比信息熵节省约40%的计算量（无对数运算）

---

2、Gini指数的数学本质

​定义 ​：从数据集中随机抽取两个样本，其类别标记不一致的概率

​计算公式​：

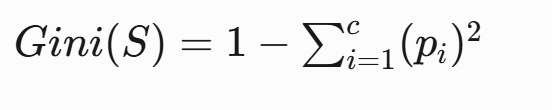
• c：类别总数
• pi：第i类样本的占比

​计算示例​：某节点有10个样本：

• 7个类别A → pA=0.7

• 3个类别B → pB=0.3

  Gini = 1 - (0.7² + 0.3²) = 1 - (0.49 + 0.09) = 0.42

3、Gini增益计算流程

1. 计算父节点Gini指数（前例得0.42）
2. 计算特征分裂后的加权Gini指数 ：
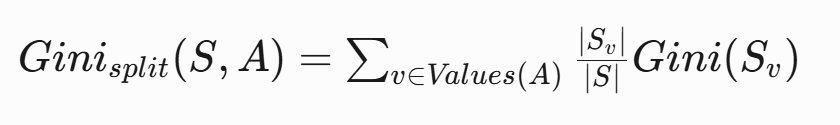
3. 计算Gini增益 ：

---

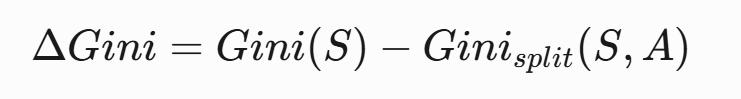
​实例演算​（天气数据集）：

天气	风速	打球
晴	弱	否
晴	强	否
阴	弱	是
雨	强	是
雨	弱	是
雨	强	否

---

第一步：计算根节点Gini指数

总样本6个：3"是"，3"否"

---

第二步：计算各特征Gini增益

1. 特征"天气"（3个取值：晴/阴/雨）

​​候选二分方案 （CART必须做二元分裂）：

1. {晴} vs {阴,雨}
2. {阴} vs {晴,雨}
3. {雨} vs {晴,阴}

​​方案1计算（{晴} vs {阴,雨}）​​：

• 左节点（晴）：2否 → Gini=0

• 右节点（阴+雨）：1阴是 + 2雨是 + 1雨否

• 加权Gini：

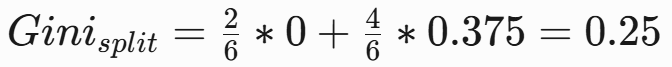
• Gini增益：

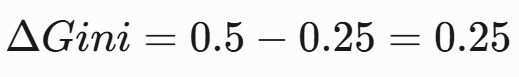
​​方案2/3计算​​（计算过程略）：

• 方案2（{阴} vs {晴,雨}）：ΔGini=0.1
• 方案3（{雨} vs {晴,阴}）：ΔGini=0.056

详细计算过程放在文章尾部

​​最佳分裂​​：选择方案1（{晴} vs {阴,雨}），ΔGini=0.25

---

2. 特征"风速"（2个取值：弱/强）

​​二元分裂方案​​：{弱} vs {强}

​​计算过程​​：

---

第三步：特征选择对比

特征	最佳分裂方案	Gini增益
天气	{晴} vs {阴,雨}	0.25
风速	{弱} vs {强}	0.056

​​决策​​：选择"天气"的{晴} vs {阴,雨}分裂方案

---

第四步：构建子树

当前分裂状态

根节点分裂：
天气是晴？
├─ 是 → 2个样本（否, 否）
└─ 否 → 4个样本（阴-是, 雨-是, 雨-是, 雨-否）

---

1：处理纯分支（晴分支）

​​左分支（天气=晴）​​：

• 样本完全纯净（全部为"否"）

• ​​直接作为叶节点​​：不打球

• C4.5改进应用：无需剪枝（已达最大纯度）

---

2：处理混合分支（阴/雨分支）

​​右分支（天气≠晴）​ ​：

4个样本：

天气	风速	打球
阴	弱	是
雨	强	是
雨	弱	是
雨	强	否

1. 计算当前节点Gini指数

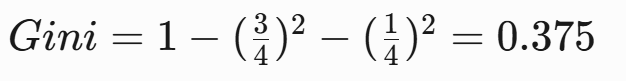
2. 候选特征选择（应用C4.5改进）

(1) 连续特征处理（无）。本例无连续特征

(2) 缺失值处理（无）。当前分支无缺失值

(3) 计算各特征增益率

​​a. 天气特征​​（已用父特征，不再考虑）

​​b. 风速特征​​：

• 分裂方案​​：{弱} vs {强}

  • 

3. 分裂决策

• 唯一可用特征：风速（ΔGini=0.125）
• ​执行分裂​（虽然增益率不高，但能提升纯度）

---

3：构建子树结构

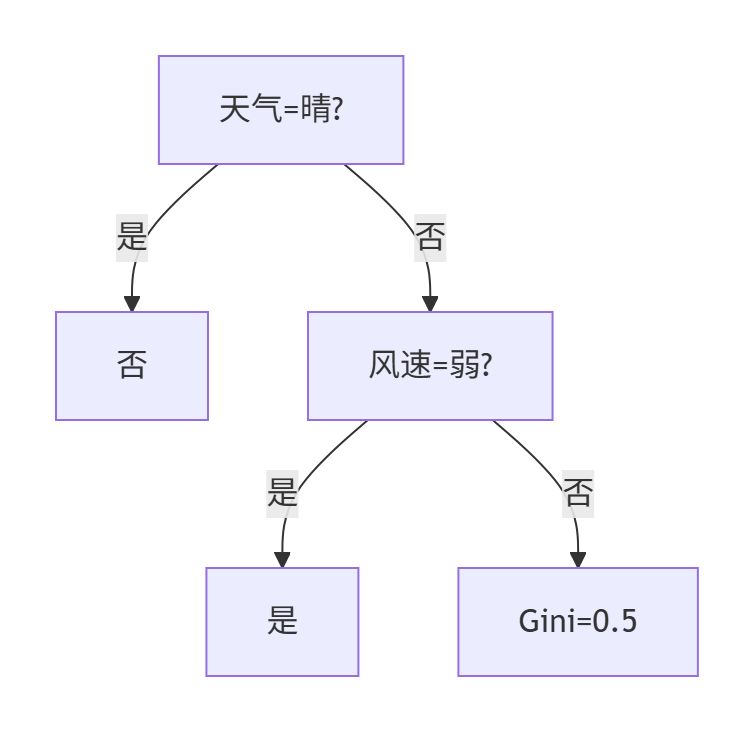
节点说明：

1. ​风速=弱​：阴-是 + 雨-是 → 纯净叶节点（打球）
2. ​风速=强​：样本：雨-是 + 雨-否 → 仍需分裂但无更多特征

---

4：后剪枝处理（关键改进）

1. ​​评估风速=强分支​​：

   • 不分裂时：直接预测多数类（是:1, 否:1 → 无法确定）
   • 替代方案：合并为叶节点并计算验证集误差
     • 若验证集支持"多数表决"（如选"是"），则剪枝

2. ​​最终优化树​​：

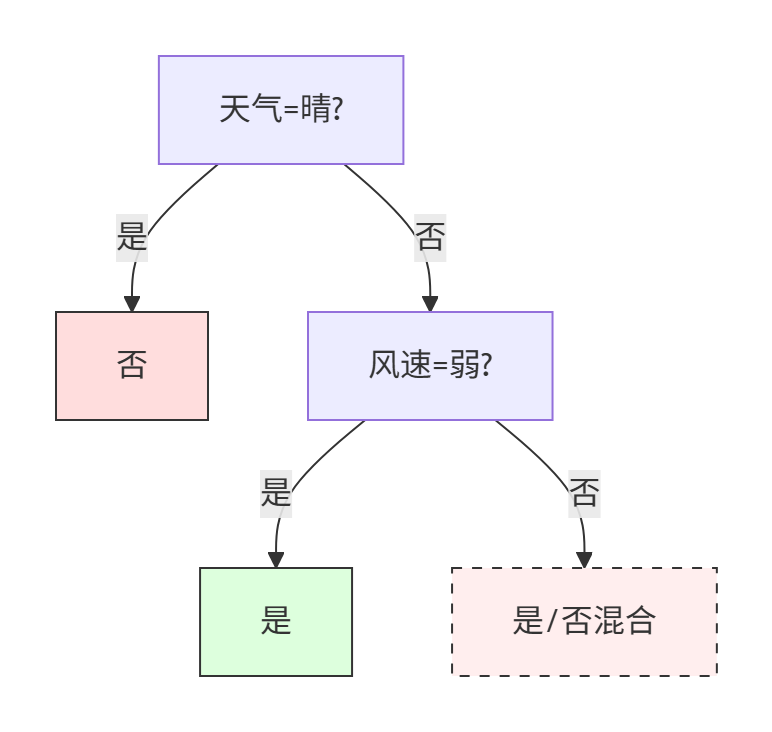
当特征信息不足时，允许存在未完全纯化的节点。

---

完整决策规则

1. 晴天 → 不打球
2. 非晴天且弱风 → 打球
3. 非晴天且强风 → 打球（剪枝后保守决策）

​​业务解释​ ​：

雨天强风时实际存在不打球样本，但C4.5通过剪枝牺牲局部精度换取泛化能力，这与ID3追求100%训练集准确率形成鲜明对比。

---

关键结论

1. ​​CART特性​​：

   • 强制二叉树结构（即使天气有3个取值也转为二元问题）
   • 对阴/雨节点的风速分裂产生混合结果，说明需要更多特征

2. ​​与ID3/C4.5对比​​：

   # ID3会直接选择天气三路分裂：
   # 晴→否, 阴→是, 雨→混合
   # CART通过二元分裂更适应集成学习

3. ​​业务解释​​：

   • 晴天绝对不打球
   • 非晴天时，弱风天打球，强风天需结合温度等其他因素判断

---

5、CART的二叉树分裂机制

​连续特征处理​：

1. 将特征值排序（如年龄[22,25,30]）
2. 计算相邻值中点（23.5, 27.5）
3. 选择使Gini增益最大的分割点

​类别特征处理​：

1. 对k个取值生成2k−1−1种可能划分
2. 选择最优二分方案（计算复杂度优化关键）

​Python实现示例​：

# 最佳分割点查找函数
def find_best_split(X, y):
    best_gain = -1
    for feature in range(X.shape[1]):
        thresholds = np.unique(X[:, feature])
        for thresh in thresholds:
            left_idx = X[:, feature] <= thresh
            p_left = np.mean(y[left_idx])
            p_right = np.mean(y[~left_idx])
            
            gini_left = 1 - (p_left**2 + (1-p_left)**2)
            gini_right = 1 - (p_right**2 + (1-p_right)**2)
            
            gain = gini_parent - (len(left_idx)/len(y))*gini_left - (len(~left_idx)/len(y))*gini_right
            if gain > best_gain:
                best_gain = gain
    return best_gain

6、回归树中的方差最小化

当用于回归任务时，CART改用方差作为分裂标准：

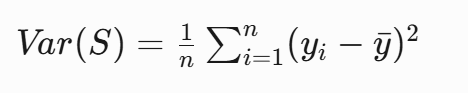
选择使加权方差最小的分割：

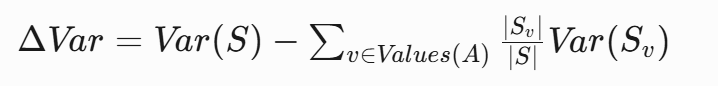
​房价预测示例​：

• 分割前方差：100
• 按"房间数≤3"分割：

  • 左节点方差：60（样本占比0.6）

  • 右节点方差：30（样本占比0.4）

    ΔVar = 100 - (0.6 * 60 + 0.4 * 30) = 64

8、CART的局限性及解决方案

局限性	解释	解决方案
过拟合	CART 会不断分裂直到纯度最大化，可能导致模型过于复杂，泛化能力差。	后剪枝（Post-Pruning）： 使用 ccp_alpha（Cost-Complexity Pruning）剪枝（scikit-learn 支持）。 预剪枝（Pre-Pruning）： 设置 max_depth、min_samples_split、min_samples_leaf 等参数限制生长。
数据不平衡	如果某一类样本占主导，CART 可能会偏向该类，忽略少数类。	类别权重： 使用 class_weight="balanced" 调整类别权重。 采样方法： 过采样少数类（SMOTE）或欠采样多数类。
不稳定性	训练数据的微小变化可能导致完全不同的树结构。	随机森林（Random Forest）： 通过多棵树的投票降低方差。 梯度提升树（GBDT/XGBoost/LightGBM）： 使用 Boosting 方式逐步修正错误。
只能生成二叉树	相比 ID3/C4.5 的多叉树，CART 的二叉树结构可能在某些数据集上效率较低。	需要多叉树 → 使用 ID3/C4.5（如 Weka 的 J48）。 需要更鲁棒的树 → 使用 条件推断树（CIT, partykit R 包）
类别特征处理低效	直接处理类别特征时，CART 可能不如信息增益（ID3/C4.5）高效。	分箱（Binning）： 对连续特征离散化，提高稳定性。 避免高基数类别特征： 对类别特征进行编码（如 Target Encoding）。
贪心分裂 （局部最优）	每次分裂只考虑当前最优，而非全局最优，可能导致次优树结构。	动态规划优化树结构 （如 OSDT 算法，但计算成本高）。

---

CART算法因其简洁高效，成为现代集成学习（如随机森林、GBDT）的基础组件。Gini指数的设计体现了机器学习中一个重要原则：​在保证效果的前提下，最简单的计算方法往往是最优选择。这种思想在XGBoost等现代算法中得到了进一步发扬光大。

---

五、Python实战（以sklearn为例）

from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

# 加载数据
iris = load_iris()
X, y = iris.data, iris.target

# 创建决策树（使用Gini指数）
model = DecisionTreeClassifier(max_depth=3, random_state=42)
model.fit(X, y)

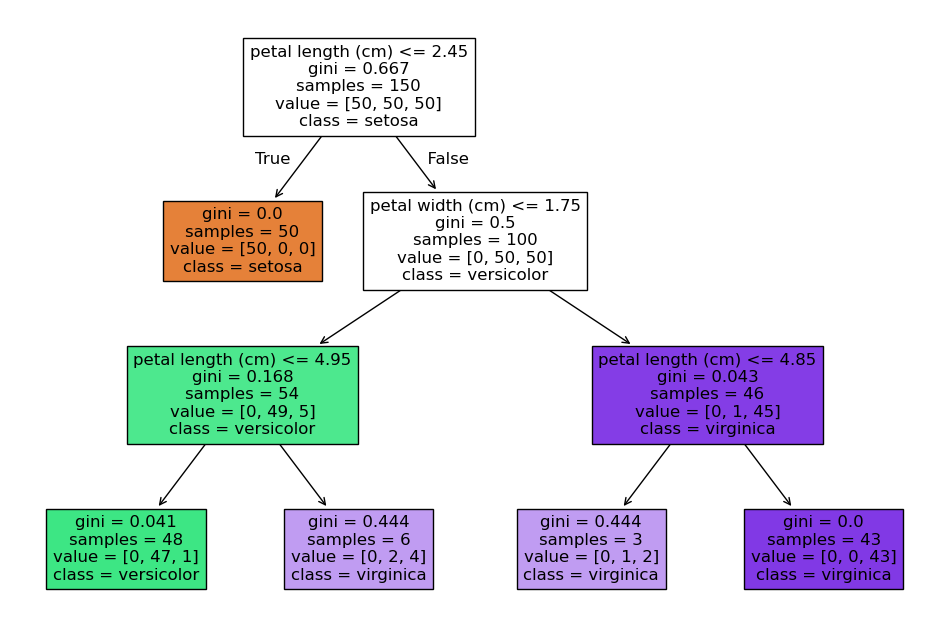
# 可视化决策树
plt.figure(figsize=(12,8))
plot_tree(model, 
          feature_names=iris.feature_names,
          class_names=iris.target_names,
          filled=True)
plt.show()

​关键参数说明​：

• max_depth：树的最大深度（控制复杂度）
• min_samples_split：节点最小分裂样本数
• criterion：分裂标准（gini/entropy）

---

六、进阶优化策略

1. 剪枝实战（预防过拟合）​：

# 后剪枝示例（代价复杂度剪枝）
pruned_model = DecisionTreeClassifier(ccp_alpha=0.02) 
pruned_model.fit(X, y)

1. ​处理连续特征​：寻找最佳分割点（如排序后取中位数）

2. ​处理缺失值​：替代分裂（surrogate splits）

---

七、决策树的双面性

​优势 ✅：

• 直观可视化（业务人员可理解）
• 无需数据标准化
• 支持混合特征（数值+类别）

​局限 ⚠️​：

• 对数据扰动敏感（小变动可能导致结构剧变）
• 容易过拟合（必须剪枝）
• 不适合学习复杂关系（如异或问题）

---

​延展思考 ​：决策树作为集成学习的基模型（如随机森林/XGBoost）时，通过"群体智慧"能极大克服自身缺陷。在实际应用中，超过80%的预测场景会优先尝试树模型家族。

八、Gini指数计算过程

方案2：{阴} vs {晴,雨} 二元分裂

1. 计算子集Gini指数

​​左节点（阴）​​：

• 样本：1是

• Gini = 1 - (1/1)² - (0/1)² = 0

​​右节点（晴+雨）​​：

• 样本：2晴否 + 3雨（2是,1否）

• 是占比 = 2/5

• 否占比 = 3/5

• Gini = 1 - (2/5)² - (3/5)² = 0.48

2. 计算加权Gini

3. 计算Gini增益

ΔGini=0.5−0.4=0.1

---

方案3：{雨} vs {晴,阴} 二元分裂

1. 计算子集Gini指数

​​左节点（雨）​​：

• 样本：2是,1否

• Gini = 1 - (2/3)² - (1/3)² ≈ 0.444

​​右节点（晴+阴）​​：

• 样本：2晴否 + 1阴是

• 是占比 = 1/3

• 否占比 = 2/3

• Gini = 1 - (1/3)² - (2/3)² ≈ 0.444

2. 计算加权Gini

3. 计算Gini增益

ΔGini=0.5−0.444=0.056