机器学习-决策树剪枝处理(C++/Python实现)

目录

一、前言

二、剪枝

[2.1 为什么要剪枝](#2.1 为什么要剪枝)

[2.2 预剪枝](#2.2 预剪枝)

[2.2.1 限制树深度](#2.2.1 限制树深度)

[2.2.2 基于验证集的早停法](#2.2.2 基于验证集的早停法)

[2.2.3 信息增益/基尼系数阈值法](#2.2.3 信息增益/基尼系数阈值法)

[2.3 后剪枝](#2.3 后剪枝)

错误率降低剪枝

[2.4 两种剪枝对比](#2.4 两种剪枝对比)

三、实现

[3.1 C++实现](#3.1 C++实现)

[3.1.1 预剪枝](#3.1.1 预剪枝)

[3.1.2 后剪枝](#3.1.2 后剪枝)

[3.1.3 可视化结果](#3.1.3 可视化结果)

[3.2 Python实现](#3.2 Python实现)

[3.2.1 预剪枝](#3.2.1 预剪枝)

[3.2.2 后剪枝](#3.2.2 后剪枝)

[3.2.3 可视化结果](#3.2.3 可视化结果)

四、总结

---

一、前言

本文直接拓展前文的内容，前文所述的算法思路，不再赘述。

本文主要实现前文涉及的三种算法的预剪枝和后剪枝，含有C++实现和Python实现。

二、剪枝

2.1 为什么要剪枝

三种算法只是选择了特征作为节点生成子树，但是并不能避免出现划分过细 的问题，也就是决策树有很多的叶子节点，模型一大，越容易过拟合 ，遇到其他问题时准确率可能不高。换句话说，就是剪枝是为了提高决策树模型的泛化能力，让模型更加优秀。

造成这个问题的主要原因是决策树中没有必要生长的枝干也生出来了 ，因此我们需要选择性地让决策树长出 ，这种把叶子节点的父节点当作叶子节点 的操作叫做剪枝，流行的几种剪枝算法都是在处理这个问题的。

剪枝算法分为两大类：预剪枝 和后剪枝。下面逐个介绍。

2.2 预剪枝

预剪枝是一类在决策树生成时，同步进行剪枝处理的算法

2.2.1 限制树深度

算法思路：

顾名思义，就是设置树的最大树高 ，把树 的生长限定在规定的范围内，这样就能减少树的分支，避免过度细分。

分析优缺点：

优点：高效，计算量小

缺点：过于简单粗暴 ，导致一些应该生长出来的枝干被一棍子打死，被认为是不该生长的，这样反而用力过度，容易出现欠拟合的情况 ；还有可能出现预设的最高的树高太高 ，导致算法失效 ，没能达到剪枝效果的情况，这种时候模型仍然过拟合。这个算法生硬地抑制树的生长 ，只适合新手入门实现，一般不会直接部署到工程中。

2.2.2 基于验证集的早停法

算法思路：
比较 长出枝干和没长出枝干的模型的准确率，如果长出枝干后模型效果更好，就保留枝干，否则剪枝。

分析优缺点：

优点：泛化能力强，逻辑直观，相比"限制树深度"算法更加灵活地调整树的生长，在工业上

缺点：需要额外划分验证集的数据出来 ，训练数据减少，噪点的影响被放大 ，可能提前停止生长 ，导致欠拟合。

2.2.3 信息增益/基尼系数阈值法

算法思路：

设置一个阈值，只有高于 这个阈值 的节点才能划分出子集。

分析优缺点：

优点：贴合决策树划分逻辑 ，可过滤对分类贡献小的划分

缺点：对阈值敏感 ，模型的好坏依赖数据分布情况(分布均匀、一些同一特点的数据集中分布等)

本文选择实现"基于验证集的早停法"

2.3 后剪枝

后剪枝是一类在决策树生成后 ，对模型进行剪枝处理的算法。

这里只介绍"错误率降低剪枝"算法

错误率降低剪枝

算法思路：

和"基于验证集的早停法"类似，我们还是通过比较剪枝前后的准确率 来决定 是否需要剪枝。

分析优缺点：

优点：逻辑直观，实现简单

缺点：依赖验证集 ，占用数据集资源，导致噪声的影响变大 ，容易使生成的模型泛化能力降低，通过后剪枝可能进一步降低模型的泛化能力，甚至导致模型欠拟合。

2.4 两种剪枝对比

| 维度\类型 | 预剪枝 | 后剪枝 |
| 优点 | 效率高 ，在构建决策树时生成； 实现简单，只需要在生成子树时比较阈值或是效果就能决定是否生成子树。 | 泛化能力往往优于预剪枝 ，处理的是整体的结构，能比较好的平衡欠拟合和过拟合； 剪枝更精准，根据实际分支评估准确度。 |
| 缺点 | 欠拟合风险高 ，终止条件过严导致树生长太浅； 一些算法的阈值难选 | 效率低，要遍历完整的树结构； |

通病	例如"基于验证集的早停法"和"错误率降低法"，都采用贪心算法 ，目光短浅， 预剪枝生成的子树时，如果存在这样的叶子节点，它的父节点的划分 导致了决策树效果变差 ，而当它长出来后整个决策树的效果比对父节点剪枝还要好 ，但是这样的节点在处理父节点时就没有机会长出来； 后剪枝也是一样，只处理了当前的这一步，没考虑对应父节点的剪枝效果，剪枝破坏 了原来父节点作为根的子树的完整性 ，导致无法正确判断 原来的这整棵子树被剪掉后的效果 ，父节点因为这个叶子节点被剪枝了，没有被剪掉 这两种算法都可能掉入贪心陷阱 中，误把局部最优子树当作全局最优子树。

三、实现

由于是对前一篇文章的拓展，就直接看代码了

同样，实现的代码还是放到了同一个仓库中管理，这次的文件夹名为DecisionTreePruning
代码仓库空降地址(github的)

下面实现，采用了留出法，即保留了一部分数据充当验证集 ，所以和K折交叉验证有同样的缺陷，对局部数据的标签敏感 ，举个例子，在只有两种标签的数据集中，如果刚好划分了一种标签为训练集、另一中标签为验证集，那么无论怎么训练，生成的决策树一定是不如意的 ，

但为了方便观察，且本次实验的数据集分布比较均匀 ，所以不随机或者将随机值固定

3.1 C++实现

3.1.1 预剪枝

核心代码讲解：

double tree_accuracy(DecisionTreeNode* root, std::vector<std::vector<int>>& features, std::vector<int>& tags)
{
	if (!tags.size())
		return 0.0;
	double passive = 0;
	std::vector<std::vector<int>> test(features[0].size(), std::vector<int>(features.size()));
	for (int i = 0; i < features.size(); ++i)
	{
		for (int j = 0; j < features[i].size(); ++j)
		{
			test[j][i] = features[i][j];
		}
	}
	for (int i = 0; i < test.size(); ++i)
		passive += predict_type(root, test[i]) == tags[i];
	return passive / tags.size();
}

double tree_accuracy(int tag, std::vector<int>& tags)
{
	double passive = 0;
	for (int t : tags)
		passive += t == tag;
	return passive / tags.size();
}

第一个重载的tree_accuracy函数，传入的features 数据是已经转置 的，在main函数中实现的，下面看到的update_mask生成的行遍历行为处理转置，否则应该和Python实现一样是列遍历的。

为了正常使用predict_type函数，我们需要将features数据转换回以样本为行、以样本内容为列的数据 。

之后就是两个重载函数都统计正确预测出来的比率，返回。这样就实现了"基于验证集的早停法"中的准确率的计算。

DecisionTreeNode* CreateDecisionTree(std::vector<std::vector<int>>& train_fs, std::vector<int>& train_ts,
	std::vector<int> idxlist, ClassifierFunc classifier, std::vector<bool> feature_mask,
	std::vector<std::vector<int>>& verify_fs = std::vector<std::vector<int>>(), std::vector<int>& verify_ts = std::vector<int>(),
	std::vector<bool> mask = std::vector<bool>(), bool pruning = false)
{
	std::vector<std::vector<int>> sub_features = splitlist(feature_mask, train_fs);
	std::vector<int> sub_tags = splitlist(feature_mask, train_ts);

	auto taglist = bincount(sub_tags);
	int max_tag = std::max_element(taglist.begin(), taglist.end()) - taglist.begin();

	if (unique(sub_tags).size() == 1)
		return new DecisionTreeNode(sub_tags[0], -1, max_tag, true);
	if (idxlist.size() == 0)
		return new DecisionTreeNode(max_tag, -1, max_tag, true);


	int idx = classifier(sub_features, sub_tags);
	if (idx >= sub_tags.size())
		CatchErr("CreateDecisionTree: 最大值索引超过数据集大小");
	if (idx == -1)
		CatchErr("出现空数据集，导致信息增益率计算出错");

	std::vector<int> values(sub_features[idx]);
	auto typenumlist = unique(values);

	std::vector<int> newlist(idxlist);
	newlist.erase(newlist.begin() + idx);

	std::vector<DecisionTreeNode*> children;
	children.reserve(typenumlist.size());
	for (int t : typenumlist)
	{
		std::vector<bool> new_feature_mask(feature_mask);
		for (int i = 0; i < new_feature_mask.size(); ++i)
			new_feature_mask[i] = new_feature_mask[i] && (train_fs[idx][i] == t);

		std::vector<bool> update_mask(mask);
		if(pruning)
			for(int i = 0; i < verify_fs[idx].size(); ++i)
				update_mask[i] = update_mask[i] && (verify_fs[idxlist[idx]][i] == t);
		auto child = CreateDecisionTree(train_fs, train_ts, newlist, classifier, new_feature_mask, verify_fs, verify_ts, update_mask, pruning);
		child->val = t;
		children.push_back(child);
	}

	auto tree = new DecisionTreeNode(idx, idxlist[idx], max_tag, false, children);

	if (pruning)
	{
		auto this_verify_f = splitlist(mask, verify_fs);
		auto this_verify_t = splitlist(mask, verify_ts);
		double origin = tree_accuracy(max_tag, this_verify_t);
		double modify = tree_accuracy(tree, this_verify_f, this_verify_t);
		std::cout << "--->> origin: " << origin << ", modify: " << modify << " <<---" << std::endl;

		if (origin >= modify)
			return new DecisionTreeNode(max_tag, -1, max_tag, true);
	}
	return tree;
}

前文我们已经解释过了如何生成，由于ID3、C4.5和CART都是一样的生成决策树的逻辑，我们只需要修改出一个决策树算法核心 ，拓展出两个外调接口，就能灵活选择对应的算法创建树了。

最大的变化是，添加了验证集特征和验证集标签数据变量，为了不让数据大量进行拷贝 ，小编利用掩码 ，到每一次递归在新的函数里面生成一份有效数据集 ，在递归调用时无需额外拷贝参数，降低内存开销 ，遇到很大的数据集时就只需要更少的时间就能生成决策树。
掩码 ，就是生成一份有勾选框的"清单"，需要的打勾，不要的不打勾，为生成筛选出有效数据作准备 。

同时，优化了splitlist 两个重载函数，优化的方面在减少传参拷贝、reserve空间，减少多余的操作。

最后，我们利用掩码做路径追踪，需要预剪枝的我们就进入预剪枝多出来的代码块中。比较改变前后的准确率，做出选择。

3.1.2 后剪枝

核心代码：

DecisionTreeNode* post_pruning(DecisionTreeNode* root, std::vector<std::vector<int>>& verify_fs, std::vector<int>& verify_ts)
{
	if (root == nullptr)
		return nullptr;
	if (root->is_leaf)
		return root;
	for (int i = 0; i < root->Children.size(); ++i)
		root->Children[i] = post_pruning(root->Children[i], verify_fs, verify_ts);

	DecisionTreeNode* node = new DecisionTreeNode(root->major_type, -1, root->major_type);
	double origin = tree_accuracy(root, verify_fs, verify_ts);
	double modify = tree_accuracy(node, verify_fs, verify_ts);

	if (origin >= modify)
		return root;
	else
		return node;
}

你没看错，后剪枝代码就是这么少，但是递归的开销还是很大的，为了实现剪枝的算法，我们需要提前将当前节点下的最多的结果类型保存下来 ，在DecisionTreeNode中添加一个major_type成员专门负责记录这个数据。

采用后序遍历 的方法来实现决策树的递归遍历，因为后序遍历符合我们需要从最下面的非叶子节点开始做剪枝算法处理 的需求。比较两颗子树的准确率 ，选择合适的保留下来，返回最终选择的节点。

3.1.3 可视化结果

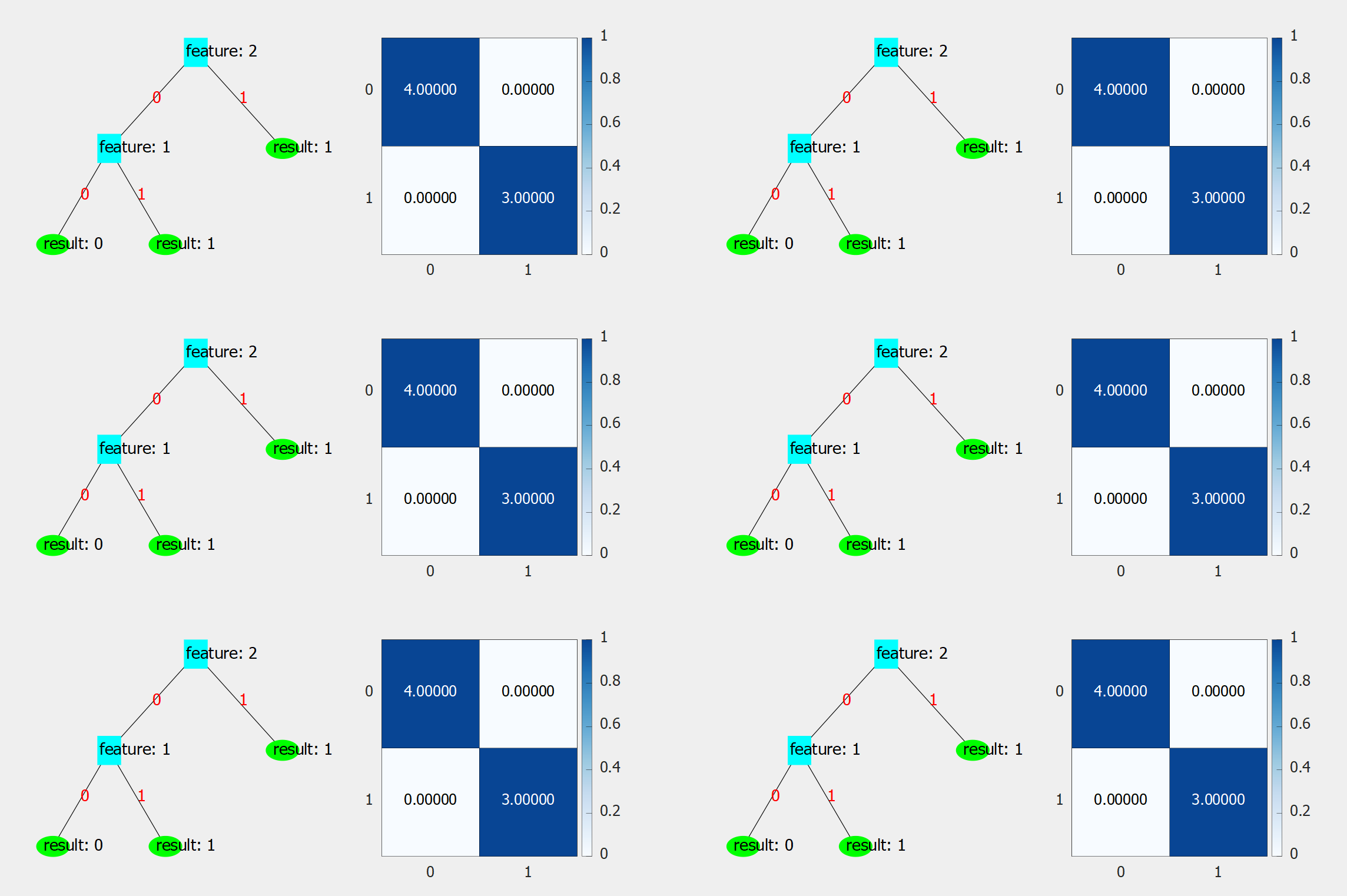
3.2 Python实现

3.2.1 预剪枝

def core_create_tree(features: np.ndarray, tags: np.ndarray, idx_list: list[int],
                     classifier: callable([[np.ndarray, np.ndarray], int]),
                     verify_f: np.ndarray = None, verify_t: np.ndarray = None,
                     mask: np.ndarray = None, pruning = False
                     ) -> DecisionTreeNode | None:
    max_tag = int(np.argmax(np.bincount(tags)))
    if len(np.unique(tags)) == 1:  # 如果预测类别只有一种，就停止决策树的生长
        return DecisionTreeNode(-1, tags[0], max_tag)
    if len(idx_list) == 0:  # 如果特征类别没了，没有能选择的特征，就停止决策树的生长
        return DecisionTreeNode(-1, max_tag, max_tag)

    # 获取最佳特征下标
    idx = classifier(features, tags)
    if idx == -1:
        return None
    value = features[:, idx]  # 获取特征列
    classes = np.unique(value)  # 获取特征类别

    # 更新数据集
    new_features = np.delete(features, obj=idx, axis=1)
    new_idx_list = copy.deepcopy(idx_list)
    new_idx_list.pop(idx)  # 删除特征列表中被选中的特征

    # 生成子节点
    children = []
    for cls in classes:
        # 划分数据集
        sub_list = (cls == value)
        sub_features = new_features[sub_list]
        sub_tags = tags[sub_list]

        update_mask = (cls == verify_f[:, idx_list[idx]]) & mask if not mask is None else mask
        child = core_create_tree(sub_features, sub_tags, new_idx_list, classifier,
                                 verify_f, verify_t, update_mask, pruning)
        child.val = cls
        children.append(child)

    root = DecisionTreeNode(idx_list[idx], idx, max_tag, children)
    if pruning:
        current_ver_features = verify_f[mask]
        current_ver_tags = verify_t[mask]

        # 获取生成子树前的精度
        pre = tree_accuracy(None, max_tag, current_ver_tags)
        print(f"生成子树前的精度：{pre}")

        # 获取分裂后的精度
        mod = tree_accuracy(root, current_ver_features, current_ver_tags)
        print(f"生成子树后的精度：{mod}")

        if mod <= pre:
            return DecisionTreeNode(-1, max_tag, max_tag)

    return root

和C++实现一样，由于我们是在生成子树后才进行比较的，所以剪枝的相关操作都可以被放到一个代码块中实现，算法思路很简单**，获取准确率，比较出最佳的子树，返回子树**。递归逻辑和前文讲的一样，就不重复了。至于掩码的部分，就不再优化了，读者可以执行优化训练集的掩码(好吧，小编抽个时间再优化一下，到时候没看到这句话就是优化完了)。

3.2.2 后剪枝

def post_pruning(root: DecisionTreeNode, verify_f: np.ndarray, verify_t: np.ndarray) -> DecisionTreeNode | None:
    if root is None:
        return None
    if root.is_leaf:
        return root
    for idx, child in enumerate(root.children):
        root.children[idx] = post_pruning(child, verify_f, verify_t)
    post = tree_accuracy(root, verify_f, verify_t)
    node = DecisionTreeNode(-1, root.major_tag, root.major_tag)
    mod = tree_accuracy(node, verify_f, verify_t)

    return node if mod > post else root

和C++实现一样简单，先后序遍历，再比较准确率，选择最佳子树返回。

3.2.3 可视化结果

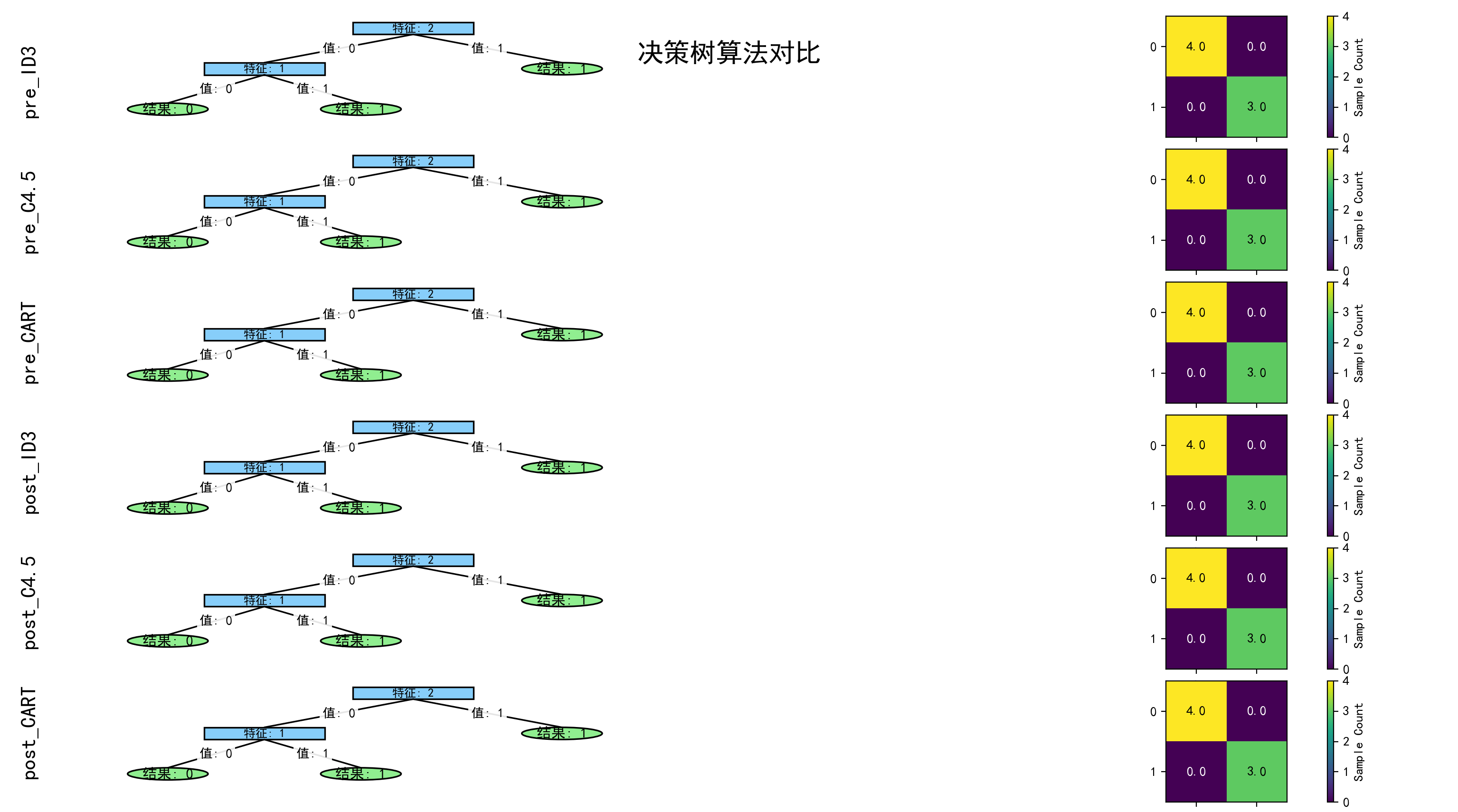
四、总结

虽然数据集太少了，很容易就准确率100%，不能明显看出泛化能力的提高，但是分类的效果和前文最终结果是一样的，也就是生成的决策树在剪枝算法处理后还是一样，就是说现在生成的这几颗决策树被认为是最优的。