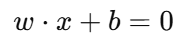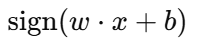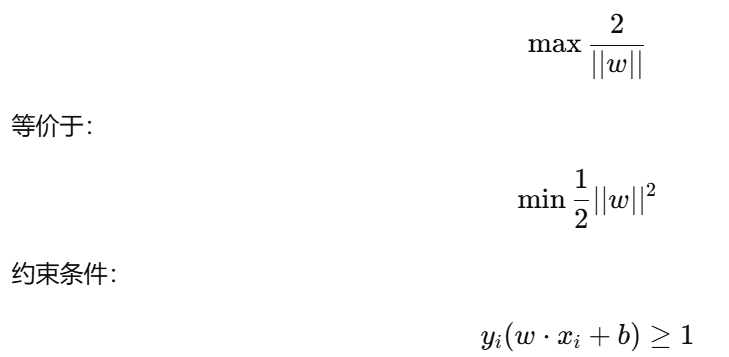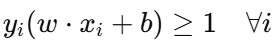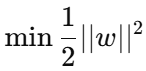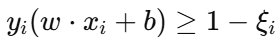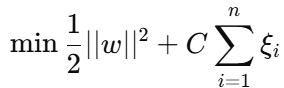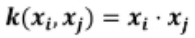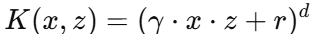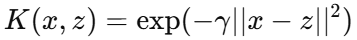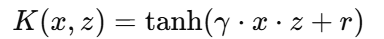机器学习——支持向量机（SVM）

支持向量机（SVM）详解与实战

概述

支持向量机（Support Vector Machine, SVM）是一种常用的监督学习算法 ，主要用于分类(SVC) （也可用于回归（SVR）、异常检测等任务）。

支持向量机（SVM）是一套统一的理论框架，既可以做分类，也可以做回归。

SVC（Support Vector Classification） → 分类任务

SVR（Support Vector Regression） → 回归任务

它们的超参数相似

都有 C、kernel、gamma、degree、coef0 等参数

核函数都支持 kernel='linear'|'poly'|'rbf'|'sigmoid' 以及自定义核

支持向量机是一种二分类模型，其基本思想是找到一个超平面，将不同类别的数据分隔开，并且使得两类数据点到超平面的距离（即间隔）最大化。

它的核心思想是：

在特征空间中找到一个最佳分割超平面（Hyperplane），使得两类样本间的间隔（Margin）最大化，同时尽可能正确分类。

这种"最大化间隔"的思路，使得 SVM 在高维空间依然有很强的泛化能力，并且在样本量不大但特征维度很高时表现优秀（如文本分类、人脸识别等）。

SVM不仅可以处理线性可分问题，还可以通过核函数处理非线性可分问题

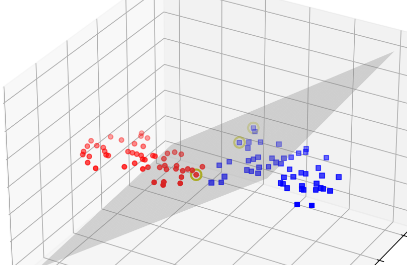
核心原理

线性可分 SVM

假设样本是线性可分的（可以用一条直线或一个平面完全分开），SVM 会找到一条最优超平面：

w：法向量，决定超平面的方向

b：偏置项，决定超平面的位置

分类规则：

输出 > 0 ⇒ 类别 +1

输出 < 0 ⇒ 类别 -1

最大化间隔Margin公式：

硬间隔和软间隔

1. 硬间隔（Hard Margin SVM）

1.1 定义

硬间隔假设数据是线性可分的 ，也就是说，存在一个超平面可以完全正确地将不同类别的样本分开，而且没有任何分类错误。

数学约束：

其中：

yi 是标签（+1 或 -1）

w 是法向量，bb 是偏置项

w⋅xi+b 是样本到超平面的函数值

目标函数：

（等价于最大化间隔）

1.2 特点

优点：数学简单、解法直接，能得到最宽的间隔。

缺点：对噪声和异常值非常敏感，一旦有一个样本被错误分类，整个模型就无法找到可行解。

2. 软间隔（Soft Margin SVM）

2.1 定义

现实数据往往线性不可分 ，或者存在噪声、异常值。

软间隔 SVM 引入了松弛变量 ξi≥0\xi_i \ge 0，允许部分样本越过间隔边界 甚至被错误分类，但会在目标函数中对这些错误进行惩罚。

数学约束：

目标函数：

第一项：最大化间隔

第二项：惩罚越界样本

C：惩罚系数（控制间隔与误差的平衡）

2.2 特点

优点：更鲁棒（Robust），可以处理含有噪声的数据集。

缺点：需要调节参数 C，否则可能欠拟合或过拟合。

2.3 C 的影响

C 大 ⇒ 惩罚错误分类样本很重 ⇒ 更贴合训练集（间隔变窄，可能过拟合）

C 小 ⇒ 容忍更多分类错误 ⇒ 间隔更宽（可能欠拟合）

3. 硬间隔 vs 软间隔对比表

特性硬间隔（Hard Margin）软间隔（Soft Margin）

数据要求线性可分，无噪声可线性不可分，可有噪声

允许误分类不允许允许（受 C 控制）

对异常值敏感非常敏感相对不敏感

计算复杂度较低较高（多了松弛变量和参数调节）

实际应用较少（理想情况）常用（现实数据）

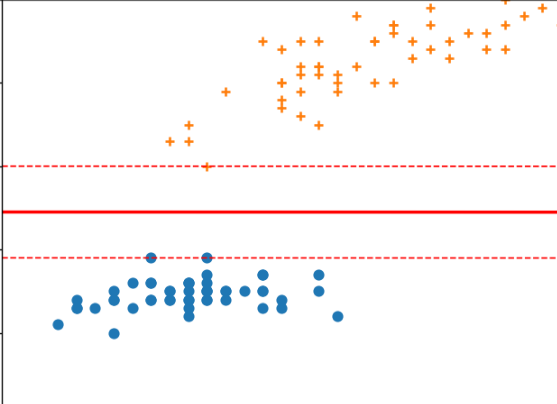
硬间隔：所有点都在间隔之外

软间隔：噪声点可能落在间隔内，甚至错分

特性	硬间隔（Hard Margin）	软间隔（Soft Margin）
数据要求	线性可分，无噪声	可线性不可分，可有噪声
允许误分类	不允许	允许（受 C 控制）
对异常值敏感	非常敏感	相对不敏感
计算复杂度	较低	较高（多了松弛变量和参数调节）
实际应用	较少（理想情况）	常用（现实数据）

核函数

SVM 常用核函数详解

1. 核函数的作用

SVM 在处理非线性数据时，会使用**核函数（Kernel Function）**将数据从低维空间映射到高维空间，使得在高维空间中可以用超平面实现线性分割。

这个过程被称为 核技巧（Kernel Trick）：

直接计算高维空间中的内积，而不需要显式地做高维映射，大幅减少计算成本。

2. 常用核函数类型

2.1 线性核（Linear Kernel）

公式：

含义：

相当于不做任何映射，直接在原特征空间中找分隔超平面

适合数据本身就是线性可分的场景

scikit-learn 调用：
复制代码
from sklearn.svm import SVC
model = SVC(kernel='linear', C=1.0)
优点：

计算速度快，适合高维稀疏数据（如文本分类）

参数少，易调节

缺点：

无法处理非线性数据

2.2 多项式核（Polynomial Kernel）

公式：

参数：

d：多项式次数（degree）

r：常数项

γ：缩放因子

适用场景：

数据存在多项式关系

边界曲线较复杂但不需要极端弯曲

调用：
复制代码
model = SVC(kernel='poly', degree=3, gamma='scale', coef0=1)
特点：

高次多项式会让边界更加复杂，可能过拟合

低次多项式边界更平滑

2.3 高斯径向基核（RBF, Radial Basis Function）

公式：

参数：

γ（gamma）：控制高斯分布宽度

大 ⇒ 决策边界更贴合训练数据（可能过拟合）

小 ⇒ 决策边界更平滑（可能欠拟合）

适用场景：

数据分布复杂，形状不规则

默认最常用核函数

调用：
复制代码
model = SVC(kernel='rbf', gamma='scale', C=1.0)
特点：

能映射到无限维空间，分类能力强

对参数选择非常敏感

2.4 Sigmoid 核（Sigmoid Kernel）

公式：

参数：

γ：缩放因子

r：偏置

适用场景：

类似神经网络中的激活函数

在某些场景可作为替代方案

调用：
复制代码
model = SVC(kernel='sigmoid', gamma='scale', coef0=1)
特点：

在部分数据集上效果不错

但不一定满足 Mercer 定理（并非总是正定核）

3. 核函数选择建议

数据特点推荐核函数说明

线性可分、高维稀疏 linear 快速、简单

存在多项式关系 poly 可调节 degree 控制边界复杂度

边界形状复杂 rbf 默认首选，泛化能力强

类似神经网络结构 sigmoid 较少用，特殊场景

数据特点	推荐核函数	说明
线性可分、高维稀疏	`linear`	快速、简单
存在多项式关系	`poly`	可调节 degree 控制边界复杂度
边界形状复杂	`rbf`	默认首选，泛化能力强
类似神经网络结构	`sigmoid`	较少用，特殊场景

超参数

参数名默认值作用调参建议

kernel 'rbf' 核函数类型：'linear'、'poly'、'rbf'、'sigmoid' 或自定义核 - 数据线性可分：linear - 非线性数据：rbf（默认） - 多项式关系：poly

C 1.0 惩罚系数，控制间隔与误分类的权衡大 ⇒ 更贴合训练集（可能过拟合）小 ⇒ 间隔更宽（可能欠拟合）常用范围：[0.1, 10]

degree 3 多项式核的次数（仅 kernel='poly' 有效）一般用 2 或 3，次数过高容易过拟合

gamma 'scale' RBF、多项式、Sigmoid 核的 γ 参数，控制高斯宽度 'scale'（推荐，= 1 / (n_features × X.var)）'auto'（= 1 / n_features）也可手动设置数值

coef0 0.0 多项式核和 Sigmoid 核的常数项控制边界形状，通常 0~1 之间调节

shrinking True 是否使用收缩启发式加快计算一般保持 True，速度更快

probability False 是否启用概率估计（predict_proba）开启会增加计算成本，调参阶段建议先关掉

tol 1e-3 停止迭代的容忍度越小越精确，训练时间越长

max_iter -1 最大迭代次数（-1 表示不限制）调大可解决收敛警告

C（惩罚系数）

大 ⇒ 尽量分类正确，间隔小（可能过拟合）

小 ⇒ 间隔大，容忍错误分类（可能欠拟合）

gamma（RBF 核参数）

大 ⇒ 决策边界更贴合训练集，容易过拟合

小 ⇒ 决策边界更平滑，可能欠拟合

参数名	默认值	作用	调参建议
kernel	`'rbf'`	核函数类型：`'linear'`、`'poly'`、`'rbf'`、`'sigmoid'` 或自定义核	- 数据线性可分：`linear` - 非线性数据：`rbf`（默认） - 多项式关系：`poly`
C	`1.0`	惩罚系数，控制间隔与误分类的权衡	大 ⇒ 更贴合训练集（可能过拟合）小 ⇒ 间隔更宽（可能欠拟合）常用范围：`[0.1, 10]`
degree	`3`	多项式核的次数（仅 `kernel='poly'` 有效）	一般用 2 或 3，次数过高容易过拟合
gamma	`'scale'`	RBF、多项式、Sigmoid 核的 γ 参数，控制高斯宽度	`'scale'`（推荐，= 1 / (n_features × X.var)）`'auto'`（= 1 / n_features）也可手动设置数值
coef0	`0.0`	多项式核和 Sigmoid 核的常数项	控制边界形状，通常 0~1 之间调节
shrinking	`True`	是否使用收缩启发式加快计算	一般保持 True，速度更快
probability	`False`	是否启用概率估计（`predict_proba`）	开启会增加计算成本，调参阶段建议先关掉
tol	`1e-3`	停止迭代的容忍度	越小越精确，训练时间越长
max_iter	`-1`	最大迭代次数（-1 表示不限制）	调大可解决收敛警告

4. SVC(分类问题) 实战案例

复制代码

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import classification_report

iris = load_iris()
x = iris.data
y = iris.target

x_train, x_test, y_train, y_test = train_test_split(x,y,random_state=42)

model = SVC(kernel='linear', C=1, random_state=42)
model.fit(x_train,y_train)

y_pred = model.predict(x_test)
print(classification_report(y_test, y_pred))

结果：

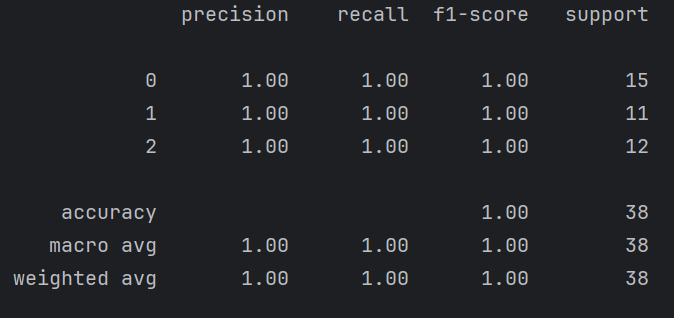
SVM 优缺点:

优点:

1.有严格的数学理论支持，可解释性强，不同于传统的统计方法能简化我们遇到的问题。

2.能找出对任务有关键影响的样本，即支持向量。

3.软间隔可以有效松弛目标函数。

4.核函数可以有效解决非线性问题。

5.最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了"维数灾难"。

6.SVM在小样本训练集上能够得到比其它算法好很多的结果。

缺点:

1.对大规模训练样本难以实施。 SVM的空间消耗主要是存储训练样本和核矩阵，当样本数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。超过十万及以上不建议使用SVM。

2.对参数和核函数选择敏感。支持向量机性能的优劣主要取决于核函数的选取，所以对于一个实际问题而言，如何根据实际的数据模型选择合适的核函数从而构造SVM算法，目前没有好的解决该核函数的选择问题。

3.模型预测时，预测时间与支持向量的个数成正比，当支持向量的数量较大时，预测计算复杂度较高。

6. 总结

SVM 通过最大化间隔获得稳健的分类效果
核函数让 SVM 能够处理非线性问题
在小样本、高维度任务中表现突出
参数（C、gamma、kernel）的选择对性能影响巨大

机器学习——支持向量机（SVM）

支持向量机（SVM）详解与实战

概述

核心原理

线性可分 SVM

硬间隔 和 软间隔

1. 硬间隔（Hard Margin SVM）

1.1 定义

1.2 特点

2. 软间隔（Soft Margin SVM）

2.1 定义

2.2 特点

2.3 C 的影响

3. 硬间隔 vs 软间隔 对比表

核函数

SVM 常用核函数详解

1. 核函数的作用

2. 常用核函数类型

2.1 线性核（Linear Kernel）

2.2 多项式核（Polynomial Kernel）

2.3 高斯径向基核（RBF, Radial Basis Function）

2.4 Sigmoid 核（Sigmoid Kernel）

3. 核函数选择建议

超参数

4. SVC(分类问题) 实战案例

SVM 优缺点:

6. 总结

硬间隔和软间隔

3. 硬间隔 vs 软间隔对比表