个人主页 : zxctscl
专栏 【C++】、 【C语言】、 【Linux】、 【数据结构】、 【算法】
如有转载请先通知
文章目录
- 前言
- [1. 733. 图像渲染](#1. 733. 图像渲染)
-
- [1.1 分析](#1.1 分析)
- [1.2 代码](#1.2 代码)
- [2. 200. 岛屿数量](#2. 200. 岛屿数量)
-
- [2.1 分析](#2.1 分析)
- [2.2 代码](#2.2 代码)
- [3. 695. 岛屿的最大面积](#3. 695. 岛屿的最大面积)
-
- [3.1 分析](#3.1 分析)
- [3.2 代码](#3.2 代码)
- [4. 130. 被围绕的区域](#4. 130. 被围绕的区域)
-
- [4.1 分析](#4.1 分析)
- [4.2 代码](#4.2 代码)
- [5 417. 太平洋大西洋水流问题](#5 417. 太平洋大西洋水流问题)
-
- [5.1 分析](#5.1 分析)
- [5.2 代码](#5.2 代码)
- [6 529. 扫雷游戏](#6 529. 扫雷游戏)
-
- [6.1 分析](#6.1 分析)
- [6.2 代码](#6.2 代码)
- [7 LCR 130. 衣橱整理](#7 LCR 130. 衣橱整理)
-
- [7.1 分析](#7.1 分析)
- [7.2 代码](#7.2 代码)
前言
FloodFill算法
FloodFill就是洪水灌溉,解决的就是下面这样一种模型:
解决性质相同的联通块 问题,用的方法就是
(1)dfs深度优先搜索遍历 :一条道走到黑,直到不能再走,不能再走就倒回去;
(2)bfs宽度优先搜索遍历:一层一层剥开
1. 733. 图像渲染
1.1 分析
方法一:bfs
用bfs模拟流程
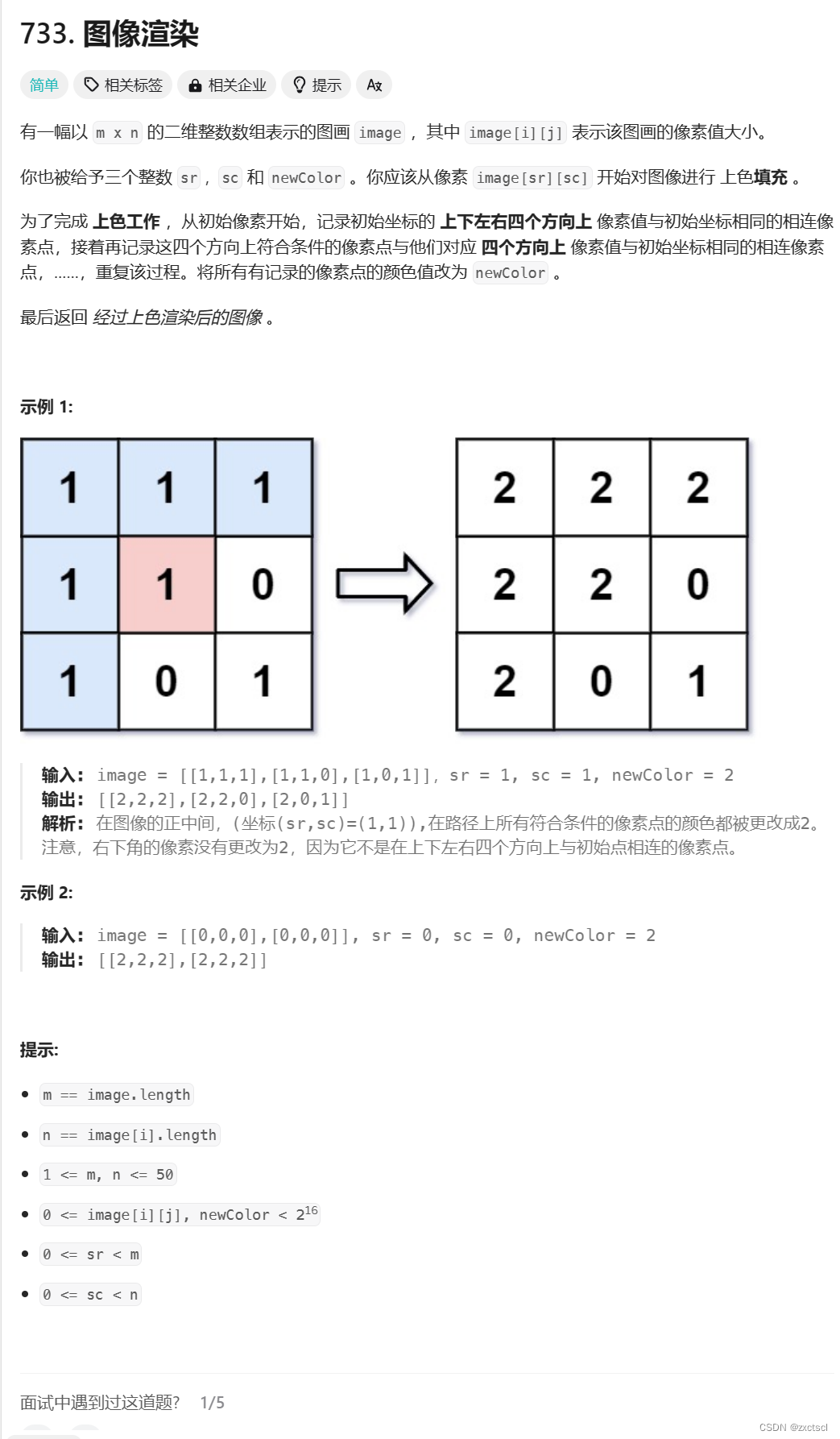
假设有这么一个矩阵,给的位置是(1,1)与(1,1)相连的所有像素相同的点,全部修改为2。
那么就一层一层搜索,就是从(1,1)开始搜索:
第一层从(1,1)开始的上下左右扫描,把(1,2)和(2,1)的值都修改为2;
第二层从(1,2)和(2,1)开始:(1,2)的扫描多加了(0,2);
(2,1)的扫描多了(2,0)和(3,1)
第三层从(0,2)、(2,0)和(3,1)开始:(0,2)多加了(0,3);(2,0)没有;(3,1)多了(3,2)
第四层从(0,3)、(3,2)发现没有了,层序遍历就完成了。
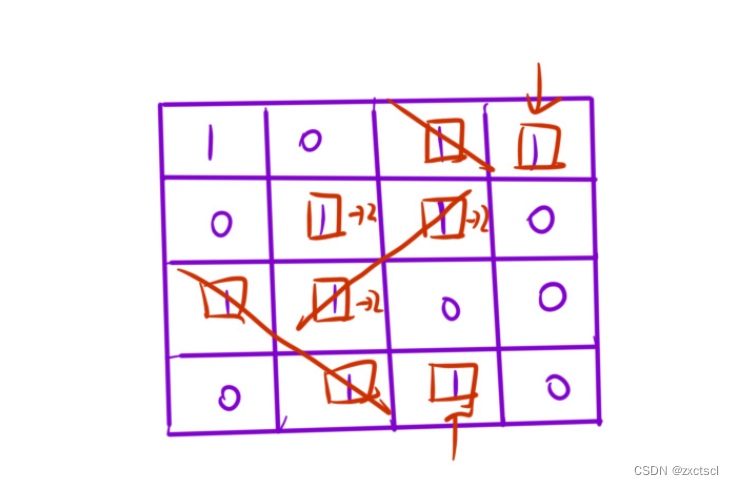
方法二:dfs :
用到坐标偏移量
横坐标上下左右偏移量就只有四个[0,0,1,-1];
同理相同位置对应纵坐标偏移量就是[-1,1,0,0]
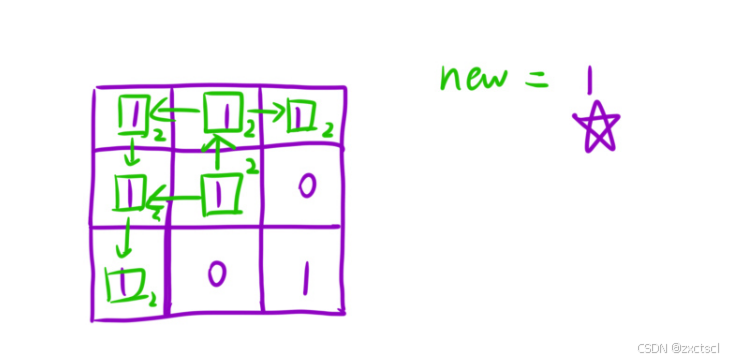
细节问题:如果给的渲染后的值是1,与原来相同,就有可能返回到原来位置,如果原始值与渲染后值相同,无需更改就直接返回就行。
1.2 代码
方法一:bfs
cpp
class Solution {
typedef pair<int,int> PII;
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color)
{
int m=image.size(),n=image[0].size();
int prev=image[sr][sc];//标记一下需要修改的像素值
if(prev==color)return image;//处理边界情况
queue<PII> q;
q.push({sr,sc});
while(q.size())
{
auto [a,b]=q.front();//取出对头
q.pop();
image[a][b]=color;
for(int i=0;i<4;i++)
{
int x=a+dx[i],y=b+dy[i];
if(x>=0&&x<m&&y>=0&&y<n&&image[x][y]==prev)
{
q.push({x,y});
}
}
}
return image;
}
};方法二:dfs
cpp
class Solution
{
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int m,n;
int prev;
public:
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color)
{
m=image.size(),n=image[0].size();
if(image[sr][sc]==color)return image;
prev=image[sr][sc];
dfs(image,sr,sc,color);
return image;
}
void dfs(vector<vector<int>>& image, int i, int j, int color)
{
image[i][j]=color;
for(int k=0;k<4;k++)
{
int x=dx[k]+i,y=dy[k]+j;
if(x>=0&&x<m&&y>=0&&y<n&&image[x][y]==prev)
{
dfs(image,x,y,color);
}
}
}
};2. 200. 岛屿数量

2.1 分析
方法一:bfs
模拟一下过程
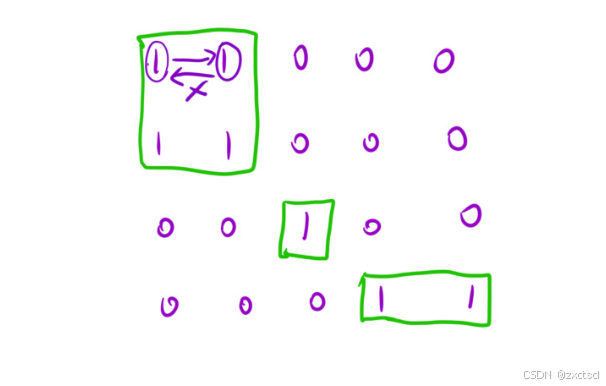
以例2模拟:从(0,0)位置开始扩展,不能扩展回去,为了不在原数组上面修改,可以给一个bool数组和原矩阵规模是一样的,然后里面如果存false,就代表这个位置没有遍历过,如果存true表示遍历过。那么从这个位置开始它的上下左右中如果有true,那么就不扫描。
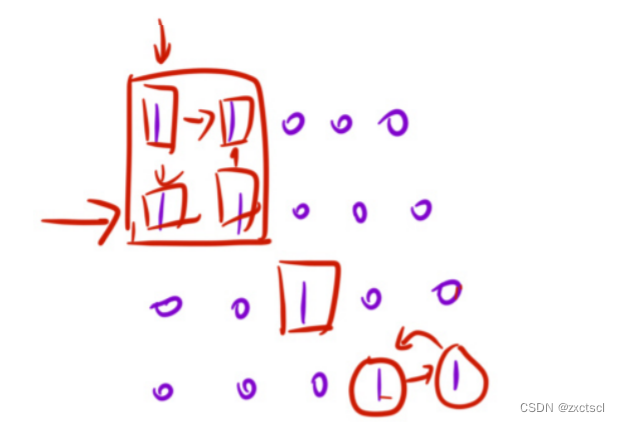
方法二:dfs :
用到坐标偏移量
横坐标上下左右偏移量就只有四个[0,0,1,-1];
同理相同位置对应纵坐标偏移量就是[-1,1,0,0]
用布尔类型二维数组标记一下是否遍历过
2.2 代码
方法一:bfs
cpp
class Solution {
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
bool vis[301][301];
int m,n;
public:
int numIslands(vector<vector<char>>& grid) {
m=grid.size(),n=grid[0].size();
int ret=0;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(grid[i][j]=='1'&&!vis[i][j])
{
ret++;
bfs(grid,i,j);
}
}
}
return ret;
}
void bfs(vector<vector<char>>&grid,int i,int j)
{
queue<pair<int,int>>q;
q.push({i,j});
vis[i][j]=true;
while(q.size())
{
auto [a,b]=q.front();
q.pop();
for(int k=0;k<4;k++)
{
int x = a + dx[k], y = b + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y]=='1'&&!vis[x][y])
{
q.push({ x,y });
vis[x][y]=true;
}
}
}
}
};方法二:dfs
cpp
class Solution {
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
bool vis[301][301];
int m,n;
public:
int numIslands(vector<vector<char>>& grid) {
m=grid.size(),n=grid[0].size();
int ret=0;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(grid[i][j]=='1'&&!vis[i][j])
{
ret++;
dfs(grid,i,j);
}
}
}
return ret;
}
void dfs(vector<vector<char>>&grid,int i,int j)
{
vis[i][j]=true;
for(int k=0;k<4;k++)
{
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y]=='1'&&!vis[x][y])
{
dfs(grid,x,y);
}
}
}
};3. 695. 岛屿的最大面积

3.1 分析
方法一:bfs
和上面那题类似,就加了一个在bfs里面统计一下面积,然后再返回的这些面积里面找到最大的那个就行。
方法二:dfs :
dfs也和和上面那题类似,就加了一个在dfs里面统计一下面积,然后再返回的这些面积里面找到最大的那个就行。
3.2 代码
方法一:bfs
cpp
class Solution {
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
bool vis[51][51];
int m, n;
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
m = grid.size(), n = grid[0].size();
int ret = 0;
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (grid[i][j] == 1 && !vis[i][j])
{
ret=max(ret, bfs(grid, i, j));
}
}
}
return ret;
}
int bfs(vector<vector<int>>& grid, int i, int j)
{
queue<pair<int, int>>q;
q.push({ i,j });
vis[i][j] = true;
int count = 1;
while (q.size())
{
auto [a, b] = q.front();
q.pop();
for (int k = 0; k < 4; k++)
{
int x = a + dx[k], y = b + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && !vis[x][y])
{
q.push({ x,y });
vis[x][y] = true;
count++;
}
}
}
return count;
}
};方法二:dfs
cpp
class Solution {
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
bool vis[51][51];
int m, n,count;
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
m = grid.size(), n = grid[0].size();
int ret = 0;
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
if (grid[i][j] == 1 && !vis[i][j])
{
count=0;
ret=max(ret, dfs(grid, i, j));
}
}
}
return ret;
}
int dfs(vector<vector<int>>& grid, int i, int j)
{
count++;
vis[i][j] = true;
for (int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && !vis[x][y])
{
dfs(grid,x,y);
}
}
return count;
}
};4. 130. 被围绕的区域
4.1 分析
方法一:bfs
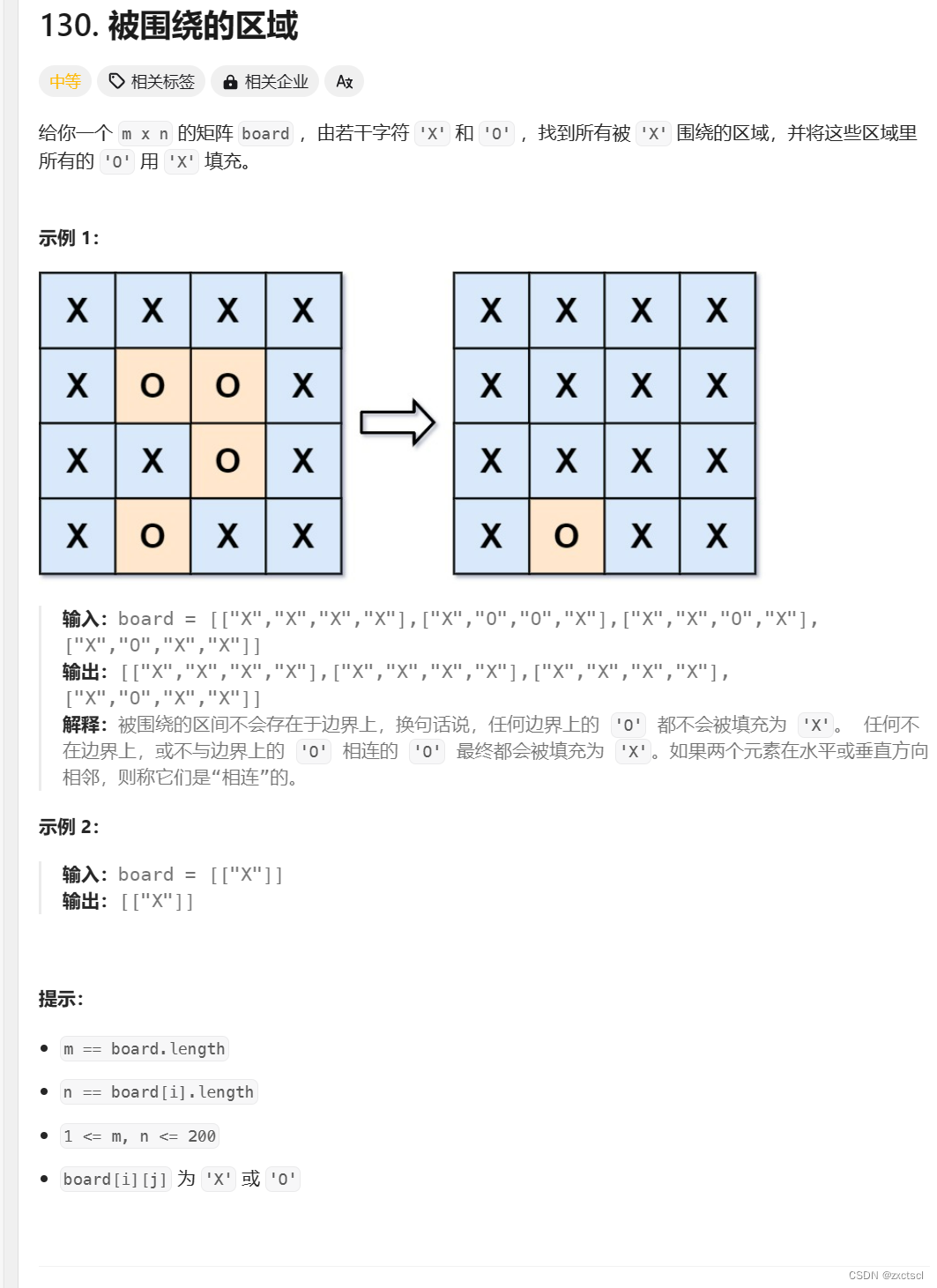
如果直接开始模拟,那么与边缘相关的联通块就不好做。那么就从与边缘相关的连通块开始做,先遍历四条变,如果边上有0,就先对它们来一个层序遍历,然后把这些位置全部修改为无关的字符。那么接下来就只需要遍历矩阵,把里面的0都修改为x就可以,因为没有被包围的四边已经处理了,剩下的就是一定被包围的。最后在把无关的字符再改回去就可以了。
这个方法叫正难则反,先处理边界上0,改为.,再扫描完矩阵后,还原。
方法二:dfs
与方法一类似,先处理与边界相连的区域全部处理,剩下的0就自然都在里面。
遇到边界里面有0改为.,再扫描完矩阵后,还原。把里面的0都修改为x就可以区分出来。
4.2 代码
方法一:bfs
cpp
class Solution {
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
int m, n;
public:
void solve(vector<vector<char>>& board)
{
m=board.size(),n=board[0].size();
//先处理边界o,把他们修改为a
for(int j=0;j<n;j++)
{
if(board[0][j]=='O')bfs(board,0,j);
if(board[m-1][j]=='O')bfs(board,m-1,j);
}
for(int i=0;i<m;i++)
{
if(board[i][0]=='O')bfs(board,i,0);
if(board[i][n-1]=='O')bfs(board,i,n-1);
}
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
if(board[i][j]=='O')board[i][j]='X';
else if(board[i][j]=='a')board[i][j]='O';
}
}
void bfs(vector<vector<char>>& board,int i,int j)
{
queue<pair<int, int>>q;
q.push({ i,j });
board[i][j]='a';
while(q.size())
{
auto [a,b]=q.front();
q.pop();
for (int k = 0; k < 4; k++)
{
int x = a + dx[k], y = b + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O' )
{
q.push({ x,y });
board[x][y] = 'a';
}
}
}
}
};方法二:dfs
cpp
class Solution {
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
int m, n;
public:
void solve(vector<vector<char>>& board)
{
m=board.size(),n=board[0].size();
//先处理边界o相连的联通快,把他们修改为.
for(int j=0;j<n;j++)
{
if(board[0][j]=='O')dfs(board,0,j);
if(board[m-1][j]=='O')dfs(board,m-1,j);
}
for(int i=0;i<m;i++)
{
if(board[i][0]=='O')dfs(board,i,0);
if(board[i][n-1]=='O')dfs(board,i,n-1);
}
//还原
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
if(board[i][j]=='.')board[i][j]='O';
else if(board[i][j]=='O')board[i][j]='X';
}
}
void dfs(vector<vector<char>>& board,int i,int j)
{
board[i][j] = '.';
for (int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j+ dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O' )
{
dfs(board,x,y);
}
}
}
};5 417. 太平洋大西洋水流问题
5.1 分析
bfs:
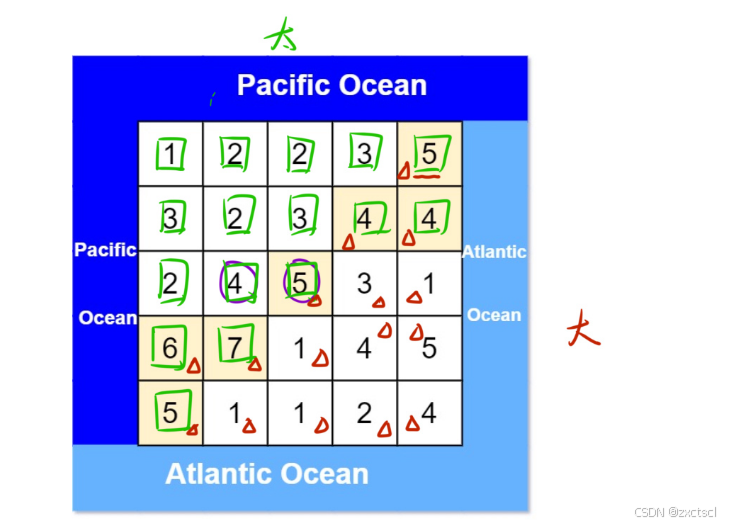
直接判断的时候,就会出现重复,此时就和上面一题类似用它的反面。
反向看:太平洋边界的水能逆向流到哪些位置,一行一行开始,遍历过的地方就不会重复。大西洋也是一样的,当两次遍历重复的地方就是既能流向太平洋,也能流向大西洋。
5.2 代码
cpp
class Solution {
int m,n;
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
public:
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights)
{
m=heights.size(),n=heights[0].size();
vector<vector<bool>> pac(m,vector<bool>(n));//太平洋
vector<vector<bool>> alt(m,vector<bool>(n));//大西洋
//1.先处理pac
for(int j=0;j<n;j++)dfs(heights,0,j,pac);
for(int i=0;i<m;i++)dfs(heights,i,0,pac);
//2.先处理alt
for(int i=0;i<m;i++)dfs(heights,i,n-1,alt);
for(int j=0;j<n;j++)dfs(heights,m-1,j,alt);
vector<vector<int>> ret;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
if(pac[i][j]&&alt[i][j])
ret.push_back({i,j});
return ret;
}
void dfs(vector<vector<int>>& heights,int i,int j, vector<vector<bool>>&vis)
{
vis[i][j]=true;
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0 && x<m && y>=0 && y<n && !vis[x][y] && heights[x][y]>=heights[i][j])
{
dfs(heights,x,y,vis);
}
}
}
};6 529. 扫雷游戏
6.1 分析
用bfs模拟一下:
判断点击位置:如果周围没有地雷就是空方格,此时递归把周围的空方格全部都打开,字符修改为B;如果有地雷就统计地雷的数量,递归统计,这个位置就记录地雷数量,递归停止到上一层。
这里用到坐标偏移量是8个
横坐标上下左右偏移量就只有四个[0,0,1,-1,-1,-1,1,1];
同理相同位置对应纵坐标偏移量就是[1,-1,0,0,-1,1,-1,1]
6.2 代码
cpp
class Solution {
int dx[8]={0,0,1,-1,1,1,-1,-1};
int dy[8]={1,-1,0,0,1,-1,1,-1};
int m,n;
public:
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click)
{
m=board.size(),n=board[0].size();
int x=click[0],y=click[1];
if(board[x][y]=='M')//一上来就点到地雷
{
board[x][y]='X';
return board;
}
dfs(board,x,y);
return board;
}
void dfs(vector<vector<char>>& board,int i,int j)
{
int count=0;
for(int k=0;k<8;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='M')
{
count++;
}
}
//周围有地雷
if(count)
{
board[i][j]=count+'0';
return;
}
else //周围没有地雷
{
board[i][j]='B';
for(int k=0;k<8;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&board[x][y]=='E')
{
dfs(board,x,y);
}
}
}
}
};7 LCR 130. 衣橱整理

7.1 分析
m=2,n=3,k=1时候,当m+n<k时候就能移动
用一个二维布尔数组记录走过的路
7.2 代码
cpp
class Solution
{
bool vis[101][101];
int m,n,cnt,ret;
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
public:
int wardrobeFinishing(int _m, int _n, int _cnt)
{
m=_m,n=_n,cnt=_cnt;
dfs(0,0);
return ret;
}
void dfs(int i,int j)
{
ret++;
vis[i][j]=true;
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&&check(x,y))
{
dfs(x,y);
}
}
}
bool check(int i,int j)
{
int tmp=0;
while(i)
{
tmp+=i%10;
i/=10;
}
while(j)
{
tmp+=j%10;
j/=10;
}
return tmp<=cnt;
}
};有问题请指出,大家一起进步!!!