《算法导论》第 13 章 - 红黑树

啊阿狸不会拉杆2025-08-10 12:21

红黑树是一种自平衡的二叉搜索树，它通过一系列规则保证树的高度始终维持在 O (log n) 级别，从而确保插入、删除、查找等操作的时间复杂度均为 O (log n)。本文将详细解析红黑树的原理、操作及实现，附带完整可运行的 C++ 代码。

思维导图

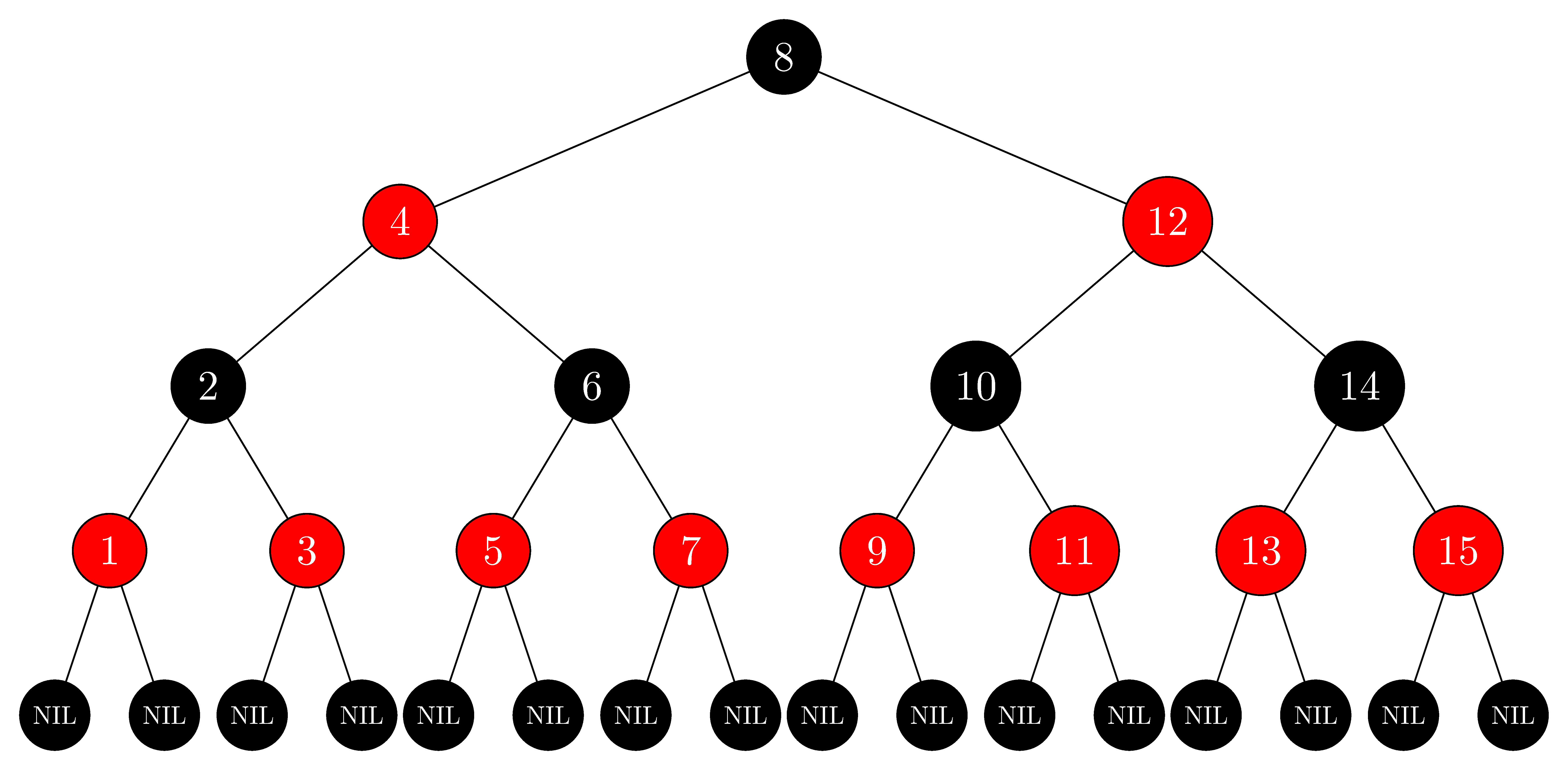
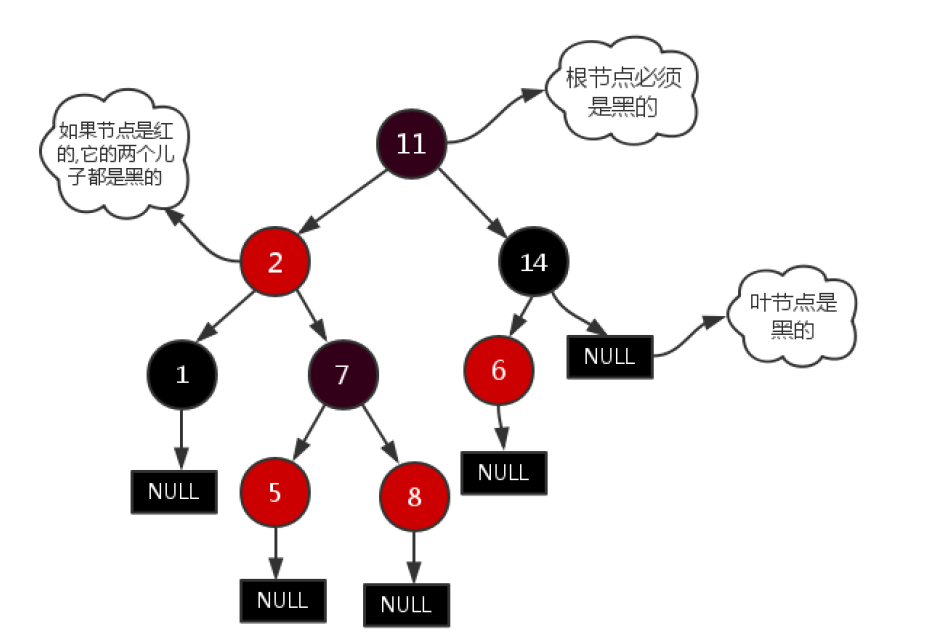
13.1 红黑树的性质

红黑树是满足以下5 个性质的二叉搜索树：

  1. 每个节点要么是红色，要么是黑色
  2. 根节点是黑色
  3. 所有叶节点（NIL 节点）是黑色（注：叶节点指没有子节点的节点，通常用一个哨兵节点表示）
  4. 如果一个节点是红色，则它的两个子节点都是黑色（即不存在连续的红色节点）
  5. 从任意节点到其所有后代叶节点的路径中，包含相同数量的黑色节点（黑高相同）

这些性质共同保证了红黑树的高度不会超过 2log (n+1)，从而实现了自平衡。

红黑树结构示意图

复制代码 
        黑
      /   \
     红    红
    / \   / \
   黑 黑 黑 黑
  /
 红
/ \
黑 黑

上图中，所有路径的黑节点数均为 2（不含叶节点），且无连续红节点，满足红黑树性质。

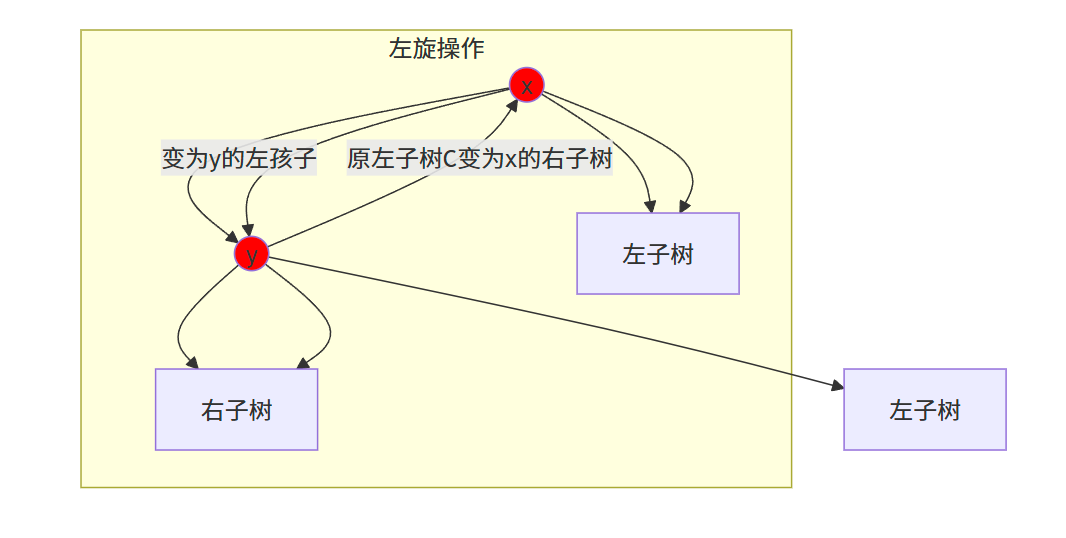
13.2 旋转

旋转是红黑树维持平衡的核心操作，分为左旋 和右旋 ，其目的是改变树的结构而不破坏二叉搜索树的性质（即左子树节点值≤父节点值≤右子树节点值）。

左旋流程图

旋转代码实现

cpp 复制代码 
#include <iostream>
using namespace std;

// 节点颜色定义
enum Color { RED, BLACK };

// 红黑树节点结构
struct Node {
    int data;       // 节点值
    Color color;    // 节点颜色
    Node *left, *right, *parent;  // 左子、右子、父节点

    // 构造函数
    Node(int val) : data(val), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};

// 红黑树类
class RedBlackTree {
private:
    Node* root;
    Node* nil;  // 哨兵节点（所有叶节点的替代，简化边界处理）

    // 左旋操作（x为要旋转的节点）
    void leftRotate(Node* x) {
        Node* y = x->right;  // y是x的右子节点
        x->right = y->left;  // 将y的左子树转为x的右子树

        if (y->left != nil) {
            y->left->parent = x;  // 若y有左子，更新其父节点为x
        }

        y->parent = x->parent;  // y的父节点更新为x的父节点

        // 处理x的父节点指向
        if (x->parent == nil) {
            root = y;  // 若x是根节点，则y成为新根
        } else if (x == x->parent->left) {
            x->parent->left = y;  // 若x是左子，则y成为其父的左子
        } else {
            x->parent->right = y;  // 若x是右子，则y成为其父的右子
        }

        y->left = x;  // x成为y的左子节点
        x->parent = y;  // x的父节点更新为y
    }

    // 右旋操作（y为要旋转的节点）
    void rightRotate(Node* y) {
        Node* x = y->left;  // x是y的左子节点
        y->left = x->right;  // 将x的右子树转为y的左子树

        if (x->right != nil) {
            x->right->parent = y;  // 若x有右子，更新其父节点为y
        }

        x->parent = y->parent;  // x的父节点更新为y的父节点

        // 处理y的父节点指向
        if (y->parent == nil) {
            root = x;  // 若y是根节点，则x成为新根
        } else if (y == y->parent->right) {
            y->parent->right = x;  // 若y是右子，则x成为其父的右子
        } else {
            y->parent->left = x;  // 若y是左子，则x成为其父的左子
        }

        x->right = y;  // y成为x的右子节点
        y->parent = x;  // y的父节点更新为x
    }

    // 中序遍历（用于打印树结构）
    void inorderTraversal(Node* node) {
        if (node != nil) {
            inorderTraversal(node->left);
            cout << node->data << "(" << (node->color == RED ? "红" : "黑") << ") ";
            inorderTraversal(node->right);
        }
    }

public:
    // 构造函数初始化
    RedBlackTree() {
        nil = new Node(0);
        nil->color = BLACK;  // 哨兵节点为黑色
        nil->left = nil;     // 哨兵的子节点指向自己，避免空指针
        nil->right = nil;
        root = nil;  // 初始根节点为哨兵
    }

    // 插入节点（简化版，仅用于测试旋转）
    void insert(int val) {
        Node* z = new Node(val);
        Node* y = nil;
        Node* x = root;

        // 找到插入位置
        while (x != nil) {
            y = x;
            if (z->data < x->data) {
                x = x->left;
            } else {
                x = x->right;
            }
        }

        z->parent = y;
        if (y == nil) {
            root = z;
        } else if (z->data < y->data) {
            y->left = z;
        } else {
            y->right = z;
        }

        z->left = nil;
        z->right = nil;
        z->color = RED;  // 新节点初始为红色
    }

    // 公开接口：执行左旋
    void performLeftRotate(int val) {
        Node* x = root;
        // 查找要旋转的节点
        while (x != nil && x->data != val) {
            if (val < x->data) {
                x = x->left;
            } else {
                x = x->right;
            }
        }
        if (x != nil) {
            leftRotate(x);
            cout << "对 " << val << " 执行左旋后: ";
            printTree();
        } else {
            cout << "未找到值为 " << val << " 的节点，无法左旋" << endl;
        }
    }

    // 公开接口：执行右旋
    void performRightRotate(int val) {
        Node* y = root;
        // 查找要旋转的节点
        while (y != nil && y->data != val) {
            if (val < y->data) {
                y = y->left;
            } else {
                y = y->right;
            }
        }
        if (y != nil) {
            rightRotate(y);
            cout << "对 " << val << " 执行右旋后: ";
            printTree();
        } else {
            cout << "未找到值为 " << val << " 的节点，无法右旋" << endl;
        }
    }

    // 打印树结构
    void printTree() {
        inorderTraversal(root);
        cout << endl;
    }
};

// 主函数：测试旋转功能
int main() {
    RedBlackTree tree;

    // 插入测试数据
    tree.insert(10);
    tree.insert(20);
    tree.insert(30);
    tree.insert(15);
    
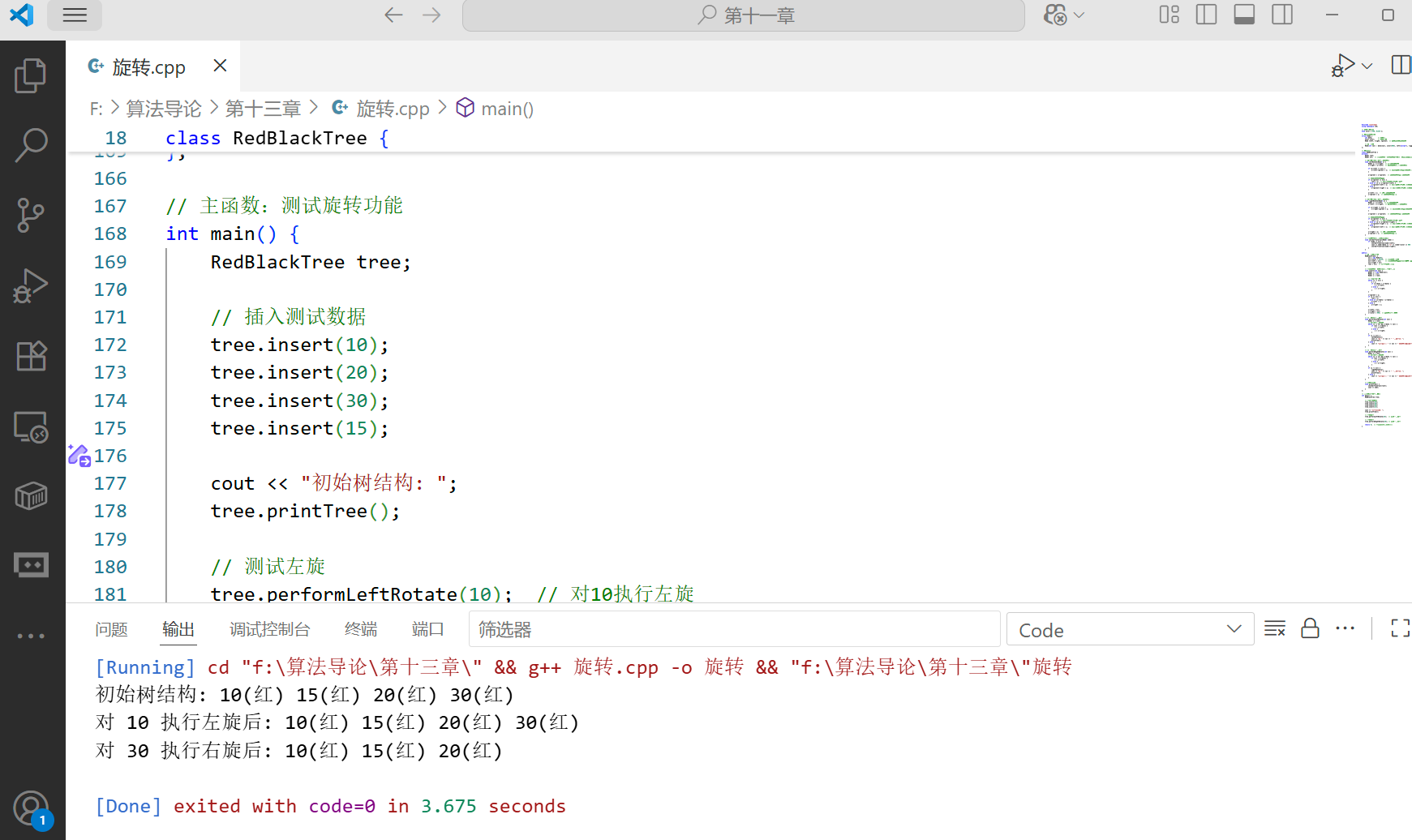
    cout << "初始树结构: ";
    tree.printTree();

    // 测试左旋
    tree.performLeftRotate(10);  // 对10执行左旋

    // 测试右旋
    tree.performRightRotate(30); // 对30执行右旋

    return 0;  // 程序入口必须有返回值
}

左旋和右旋是对称操作，时间复杂度均为 O (1)，仅改变指针指向而不修改节点值。

13.3 插入

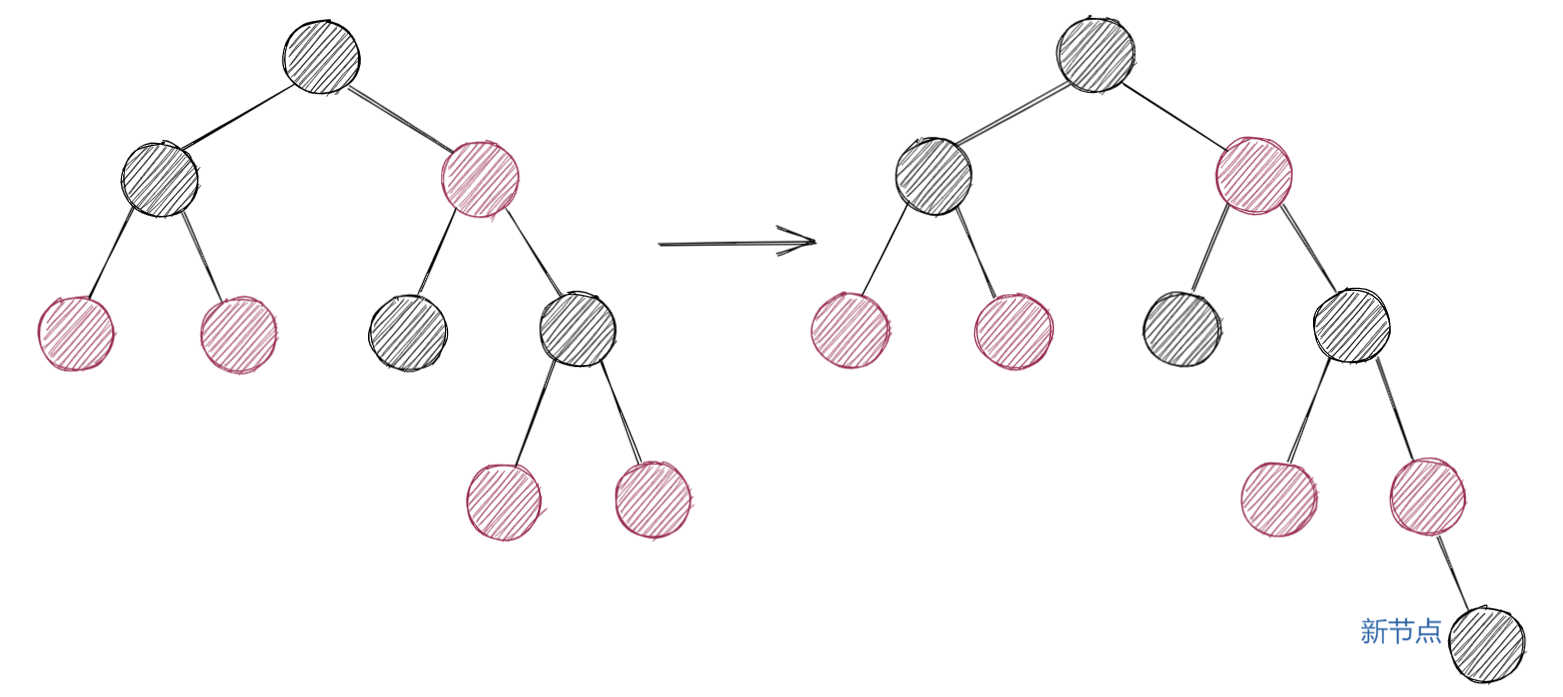
红黑树的插入流程分为两步：二叉搜索树插入 和修复红黑树性质。

插入步骤

  1. 按二叉搜索树规则插入新节点（初始颜色为红色，减少对黑高的影响）。

  2. 检查是否违反红黑树性质（若父节点为黑色则无问题；若父节点为红色则违反性质 4）。

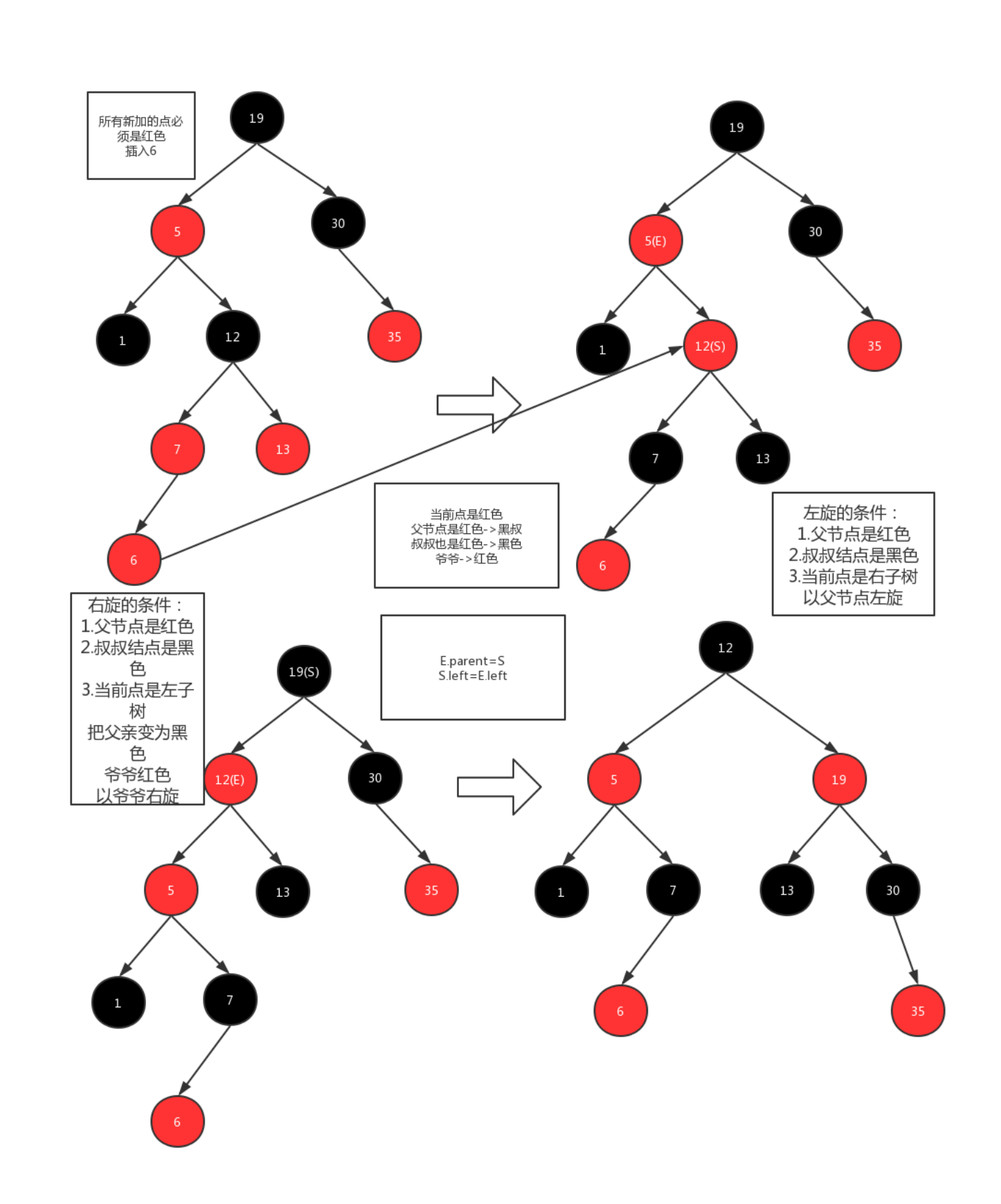
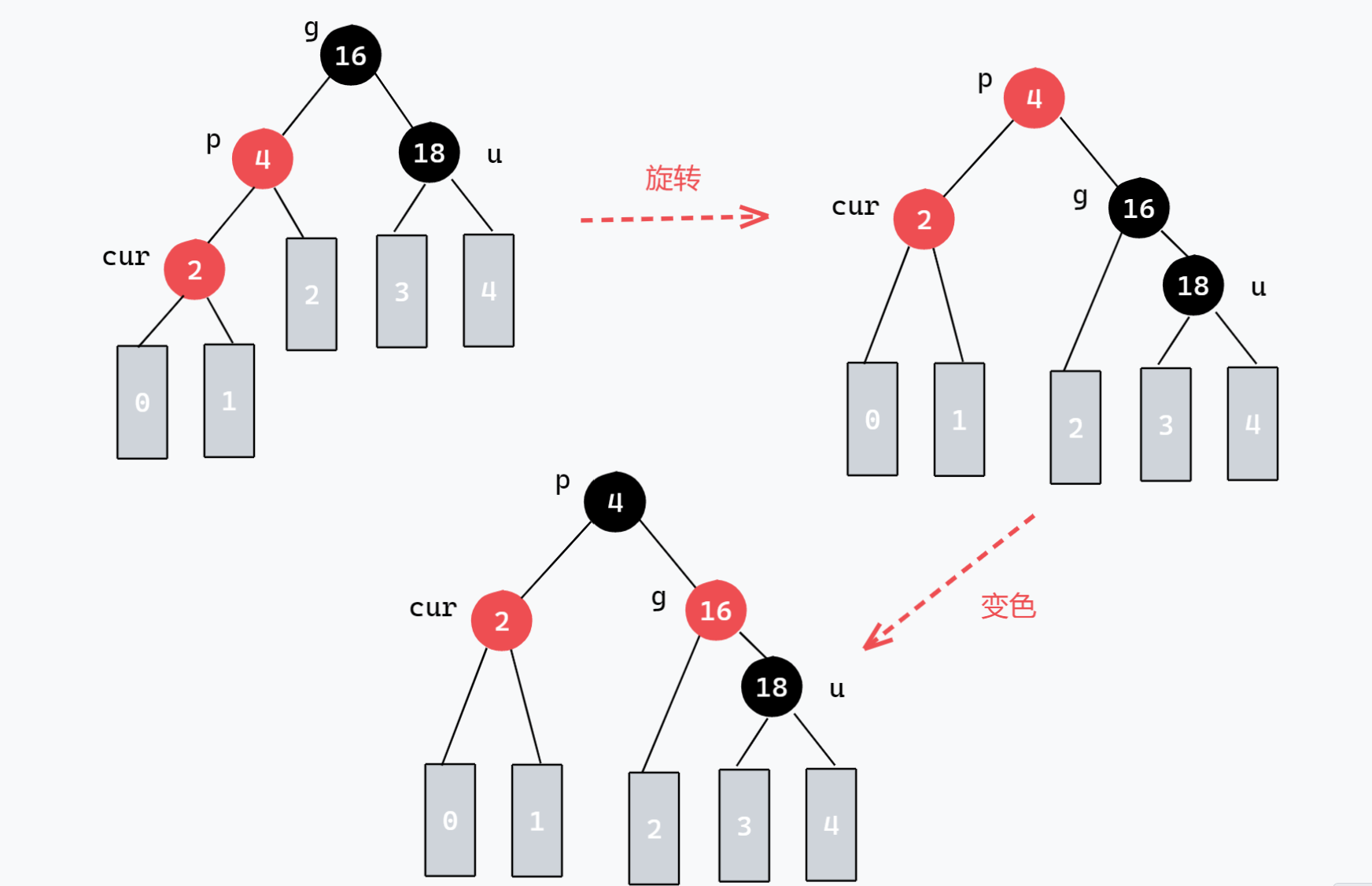
  3. 通过重新染色 和旋转修复性质，分 3 种情形处理：

    • 情形 1：叔节点为红色 → 重新染色父、叔、祖父节点。
    • 情形 2：叔节点为黑色，且新节点是 "三角" 结构（父左子 + 新右子 或 父右子 + 新左子）→ 旋转转为情形 3。
    • 情形 3：叔节点为黑色，且新节点是 "直线" 结构（父左子 + 新左子 或 父右子 + 新右子）→ 旋转 + 染色修复。

插入修复

插入代码实现（续红黑树类）

cpp 复制代码 
#include <iostream>
using namespace std;

// 节点颜色定义
enum Color { RED, BLACK };

// 红黑树节点结构
struct Node {
    int data;               // 节点值
    Color color;            // 节点颜色
    Node *left, *right, *parent;  // 左子、右子、父节点

    // 构造函数
    Node(int val) : data(val), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};

// 红黑树类
class RedBlackTree {
private:
    Node* root;
    Node* nil;  // 哨兵节点（所有叶节点的替代，简化边界处理）

    // 左旋操作（x为要旋转的节点）
    void leftRotate(Node* x) {
        Node* y = x->right;  // y是x的右子节点
        x->right = y->left;  // 将y的左子树转为x的右子树

        if (y->left != nil) {
            y->left->parent = x;  // 若y有左子，更新其父节点为x
        }

        y->parent = x->parent;  // y的父节点更新为x的父节点

        // 处理x的父节点指向
        if (x->parent == nil) {
            root = y;  // 若x是根节点，则y成为新根
        } else if (x == x->parent->left) {
            x->parent->left = y;  // 若x是左子，则y成为其父的左子
        } else {
            x->parent->right = y;  // 若x是右子，则y成为其父的右子
        }

        y->left = x;  // x成为y的左子节点
        x->parent = y;  // x的父节点更新为y
    }

    // 右旋操作（y为要旋转的节点）
    void rightRotate(Node* y) {
        Node* x = y->left;  // x是y的左子节点
        y->left = x->right;  // 将x的右子树转为y的左子树

        if (x->right != nil) {
            x->right->parent = y;  // 若x有右子，更新其父节点为y
        }

        x->parent = y->parent;  // x的父节点更新为y的父节点

        // 处理y的父节点指向
        if (y->parent == nil) {
            root = x;  // 若y是根节点，则x成为新根
        } else if (y == y->parent->right) {
            y->parent->right = x;  // 若y是右子，则x成为其父的右子
        } else {
            y->parent->left = x;  // 若y是左子，则x成为其父的左子
        }

        x->right = y;  // y成为x的右子节点
        y->parent = x;  // y的父节点更新为x
    }

    // 插入后修复红黑树性质
    void insertFixup(Node* z) {
        // 当父节点为红色时（违反性质4：红色节点的子节点必须是黑色）
        while (z->parent->color == RED) {
            // 父节点是祖父节点的左子节点
            if (z->parent == z->parent->parent->left) {  
                Node* y = z->parent->parent->right;  // 叔节点（祖父的右子）

                // 情形1：叔节点为红色
                if (y->color == RED) {
                    z->parent->color = BLACK;       // 父节点染黑
                    y->color = BLACK;               // 叔节点染黑
                    z->parent->parent->color = RED; // 祖父节点染红
                    z = z->parent->parent;          // 以祖父为新节点继续检查
                } 
                // 叔节点为黑色
                else {
                    // 情形2：叔节点为黑，且z是右子（三角结构）
                    if (z == z->parent->right) {
                        z = z->parent;  // 以父节点为基准
                        leftRotate(z);  // 左旋转为直线结构，转为情形3
                    }
                    // 情形3：叔节点为黑，且z是左子（直线结构）
                    z->parent->color = BLACK;       // 父节点染黑
                    z->parent->parent->color = RED; // 祖父节点染红
                    rightRotate(z->parent->parent); // 右旋祖父节点
                }
            } 
            // 父节点是祖父节点的右子节点（对称逻辑）
            else {  
                Node* y = z->parent->parent->left;  // 叔节点（祖父的左子）

                // 情形1：叔节点为红色
                if (y->color == RED) {
                    z->parent->color = BLACK;
                    y->color = BLACK;
                    z->parent->parent->color = RED;
                    z = z->parent->parent;
                } 
                // 叔节点为黑色
                else {
                    // 情形2：叔节点为黑，且z是左子（三角结构）
                    if (z == z->parent->left) {
                        z = z->parent;
                        rightRotate(z);  // 右旋转为直线结构，转为情形3
                    }
                    // 情形3：叔节点为黑，且z是右子（直线结构）
                    z->parent->color = BLACK;
                    z->parent->parent->color = RED;
                    leftRotate(z->parent->parent);
                }
            }
        }
        root->color = BLACK;  // 确保根节点为黑色（修复可能被破坏的性质2）
    }

    // 中序遍历（用于打印树结构，按值升序输出）
    void inorderTraversal(Node* node) {
        if (node != nil) {
            inorderTraversal(node->left);
            cout << node->data << "(" << (node->color == RED ? "红" : "黑") << ") ";
            inorderTraversal(node->right);
        }
    }

public:
    // 构造函数初始化
    RedBlackTree() {
        nil = new Node(0);
        nil->color = BLACK;  // 哨兵节点为黑色
        nil->left = nil;     // 哨兵的子节点指向自己，避免空指针
        nil->right = nil;
        root = nil;  // 初始根节点为哨兵
    }

    // 插入节点
    void insert(int val) {
        Node* z = new Node(val);
        Node* y = nil;  // y记录x的父节点
        Node* x = root;

        // 找到插入位置（类似二叉搜索树）
        while (x != nil) {
            y = x;
            if (z->data < x->data) {
                x = x->left;
            } else {
                x = x->right;
            }
        }

        z->parent = y;  // z的父节点设为y
        if (y == nil) {
            root = z;  // 树为空，z成为根节点
        } else if (z->data < y->data) {
            y->left = z;  // z成为y的左子
        } else {
            y->right = z;  // z成为y的右子
        }

        z->left = nil;   // 左右子节点设为哨兵
        z->right = nil;
        z->color = RED;  // 新节点初始为红色（减少对黑高的影响）

        insertFixup(z);  // 修复红黑树性质
    }

    // 打印树结构
    void printTree() {
        inorderTraversal(root);
        cout << endl;
    }
};

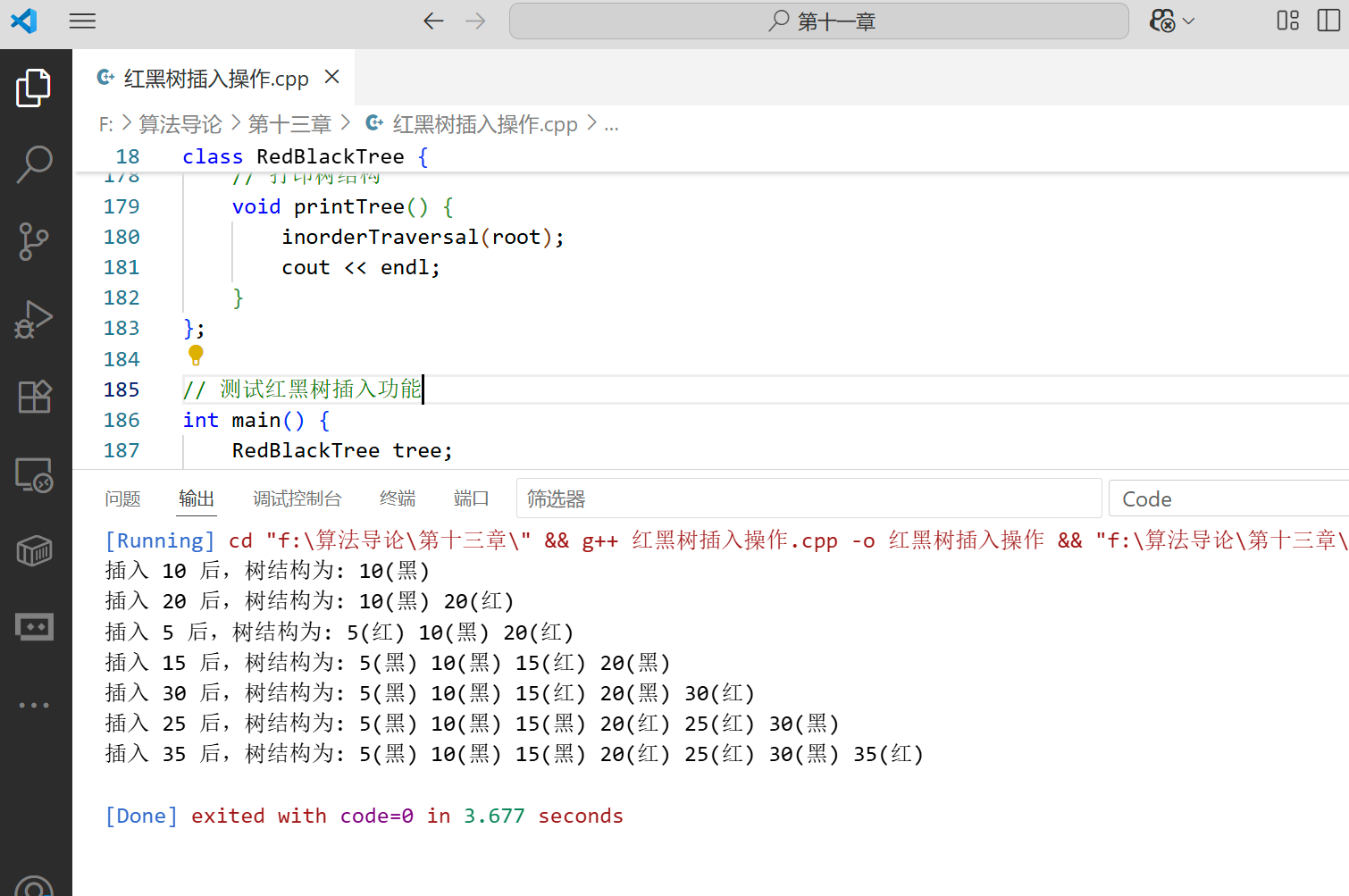
// 测试红黑树插入功能
int main() {
    RedBlackTree tree;

    // 插入测试数据
    int values[] = {10, 20, 5, 15, 30, 25, 35};
    int n = sizeof(values) / sizeof(values[0]);

    for (int i = 0; i < n; i++) {
        tree.insert(values[i]);
        cout << "插入 " << values[i] << " 后，树结构为: ";
        tree.printTree();
    }

    return 0;
}

13.4 删除

红黑树的删除是最复杂的操作，流程如下：

删除步骤

  1. 按二叉搜索树规则删除节点：
    • 若节点有 0 个或 1 个子节点，直接删除并替换。
    • 若节点有 2 个子节点，用后继节点（右子树最小节点）替换，再删除后继节点。
  2. 记录被删除节点的颜色（若为黑色则可能破坏性质 5）和替换节点。
  3. 若删除的是黑色节点，通过修复函数处理 "双黑" 问题（因黑高减少导致的性质 5 破坏）。

删除修复核心逻辑

删除黑色节点后，其位置会产生 "双黑" 标记（可理解为需要额外的黑色补偿）。修复函数通过以下方式处理：

  • 若兄弟节点为红色 → 旋转 + 染色转为兄弟节点为黑色的情形。
  • 若兄弟节点为黑色：
    • 兄弟节点的子节点均为黑色 → 兄弟染红，向上传递双黑标记。
    • 兄弟节点的左子为红（右子为黑）→ 旋转 + 染色转为右子为红的情形。
    • 兄弟节点的右子为红 → 旋转 + 染色修复双黑。

删除代码实现（续红黑树类）

cpp 复制代码 
#include <iostream>
using namespace std;

// 节点颜色定义
enum Color { RED, BLACK };

// 红黑树节点结构
struct Node {
    int data;               // 节点值
    Color color;            // 节点颜色
    Node *left, *right, *parent;  // 左子、右子、父节点

    // 构造函数
    Node(int val) : data(val), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};

// 红黑树类
class RedBlackTree {
private:
    Node* root;
    Node* nil;  // 哨兵节点（所有叶节点的替代，简化边界处理）

    // 左旋操作
    void leftRotate(Node* x) {
        Node* y = x->right;  // y是x的右子节点
        x->right = y->left;  // 将y的左子树转为x的右子树

        if (y->left != nil) {
            y->left->parent = x;  // 若y有左子，更新其父节点为x
        }

        y->parent = x->parent;  // y的父节点更新为x的父节点

        // 处理x的父节点指向
        if (x->parent == nil) {
            root = y;  // 若x是根节点，则y成为新根
        } else if (x == x->parent->left) {
            x->parent->left = y;  // 若x是左子，则y成为其父的左子
        } else {
            x->parent->right = y;  // 若x是右子，则y成为其父的右子
        }

        y->left = x;  // x成为y的左子节点
        x->parent = y;  // x的父节点更新为y
    }

    // 右旋操作
    void rightRotate(Node* y) {
        Node* x = y->left;  // x是y的左子节点
        y->left = x->right;  // 将x的右子树转为y的左子树

        if (x->right != nil) {
            x->right->parent = y;  // 若x有右子，更新其父节点为y
        }

        x->parent = y->parent;  // x的父节点更新为y的父节点

        // 处理y的父节点指向
        if (y->parent == nil) {
            root = x;  // 若y是根节点，则x成为新根
        } else if (y == y->parent->right) {
            y->parent->right = x;  // 若y是右子，则x成为其父的右子
        } else {
            y->parent->left = x;  // 若y是左子，则x成为其父的左子
        }

        x->right = y;  // y成为x的右子节点
        y->parent = x;  // y的父节点更新为x
    }

    // 插入后修复红黑树性质（完整实现才能正常测试删除）
    void insertFixup(Node* z) {
        while (z->parent->color == RED) {
            if (z->parent == z->parent->parent->left) {
                Node* y = z->parent->parent->right;
                if (y->color == RED) {
                    z->parent->color = BLACK;
                    y->color = BLACK;
                    z->parent->parent->color = RED;
                    z = z->parent->parent;
                } else {
                    if (z == z->parent->right) {
                        z = z->parent;
                        leftRotate(z);
                    }
                    z->parent->color = BLACK;
                    z->parent->parent->color = RED;
                    rightRotate(z->parent->parent);
                }
            } else {
                Node* y = z->parent->parent->left;
                if (y->color == RED) {
                    z->parent->color = BLACK;
                    y->color = BLACK;
                    z->parent->parent->color = RED;
                    z = z->parent->parent;
                } else {
                    if (z == z->parent->left) {
                        z = z->parent;
                        rightRotate(z);
                    }
                    z->parent->color = BLACK;
                    z->parent->parent->color = RED;
                    leftRotate(z->parent->parent);
                }
            }
        }
        root->color = BLACK;
    }

    // 移植节点（辅助删除操作）
    void transplant(Node* u, Node* v) {
        if (u->parent == nil) {
            root = v;
        } else if (u == u->parent->left) {
            u->parent->left = v;
        } else {
            u->parent->right = v;
        }
        v->parent = u->parent;
    }

    // 查找最小节点（用于找后继）
    Node* minimum(Node* x) {
        while (x->left != nil) {
            x = x->left;
        }
        return x;
    }

    // 删除后修复红黑树性质
    void deleteFixup(Node* x) {
        // 当x不是根节点且为黑色时需要修复（双黑问题）
        while (x != root && x->color == BLACK) {
            // x是左子节点的情况
            if (x == x->parent->left) {  
                Node* w = x->parent->right;  // 兄弟节点

                // 情形1：兄弟节点为红色
                if (w->color == RED) {
                    w->color = BLACK;         // 兄弟染黑
                    x->parent->color = RED;   // 父节点染红
                    leftRotate(x->parent);    // 左旋父节点
                    w = x->parent->right;     // 更新兄弟节点
                }

                // 情形2：兄弟节点的两个子节点均为黑色
                if (w->left->color == BLACK && w->right->color == BLACK) {
                    w->color = RED;           // 兄弟染红
                    x = x->parent;            // 向上传递双黑标记
                } else {
                    // 情形3：兄弟左子为红，右子为黑
                    if (w->right->color == BLACK) {
                        w->left->color = BLACK;  // 兄弟左子染黑
                        w->color = RED;          // 兄弟染红
                        rightRotate(w);          // 右旋兄弟
                        w = x->parent->right;    // 更新兄弟节点
                    }
                    // 情形4：兄弟右子为红
                    w->color = x->parent->color;  // 兄弟继承父节点颜色
                    x->parent->color = BLACK;     // 父节点染黑
                    w->right->color = BLACK;      // 兄弟右子染黑
                    leftRotate(x->parent);        // 左旋父节点
                    x = root;                     // 退出循环
                }
            } else {  // x是右子节点的情况（对称逻辑）
                Node* w = x->parent->left;  // 兄弟节点

                // 情形1：兄弟节点为红色
                if (w->color == RED) {
                    w->color = BLACK;
                    x->parent->color = RED;
                    rightRotate(x->parent);
                    w = x->parent->left;
                }

                // 情形2：兄弟节点的两个子节点均为黑色
                if (w->right->color == BLACK && w->left->color == BLACK) {
                    w->color = RED;
                    x = x->parent;
                } else {
                    // 情形3：兄弟右子为红，左子为黑
                    if (w->left->color == BLACK) {
                        w->right->color = BLACK;
                        w->color = RED;
                        leftRotate(w);
                        w = x->parent->left;
                    }
                    // 情形4：兄弟左子为红
                    w->color = x->parent->color;
                    x->parent->color = BLACK;
                    w->left->color = BLACK;
                    rightRotate(x->parent);
                    x = root;  // 退出循环
                }
            }
        }
        x->color = BLACK;  // 确保x为黑色，解决双黑问题
    }

    // 中序遍历（用于打印树结构）
    void inorderTraversal(Node* node) {
        if (node != nil) {
            inorderTraversal(node->left);
            cout << node->data << "(" << (node->color == RED ? "红" : "黑") << ") ";
            inorderTraversal(node->right);
        }
    }

public:
    // 构造函数初始化
    RedBlackTree() {
        nil = new Node(0);
        nil->color = BLACK;  // 哨兵节点为黑色
        nil->left = nil;     // 哨兵的子节点指向自己，避免空指针
        nil->right = nil;
        root = nil;  // 初始根节点为哨兵
    }

    // 插入节点（用于构建测试树）
    void insert(int val) {
        Node* z = new Node(val);
        Node* y = nil;
        Node* x = root;

        while (x != nil) {
            y = x;
            if (z->data < x->data) {
                x = x->left;
            } else {
                x = x->right;
            }
        }

        z->parent = y;
        if (y == nil) {
            root = z;
        } else if (z->data < y->data) {
            y->left = z;
        } else {
            y->right = z;
        }

        z->left = nil;
        z->right = nil;
        z->color = RED;

        insertFixup(z);
    }

    // 删除节点
    void deleteNode(int val) {
        Node* z = root;
        Node* y = nil;
        Node* x = nil;

        // 查找值为val的节点
        while (z != nil && z->data != val) {
            if (val < z->data) {
                z = z->left;
            } else {
                z = z->right;
            }
        }
        if (z == nil) {
            cout << "值 " << val << " 不在树中，无法删除" << endl;
            return;
        }

        y = z;
        Color yOriginalColor = y->color;  // 记录被删除节点的原始颜色

        // 处理子节点情况
        if (z->left == nil) {
            // 左子为空，用右子替换
            x = z->right;
            transplant(z, z->right);
        } else if (z->right == nil) {
            // 右子为空，用左子替换
            x = z->left;
            transplant(z, z->left);
        } else {
            // 两个子节点都存在，找后继节点
            y = minimum(z->right);
            yOriginalColor = y->color;
            x = y->right;

            if (y->parent == z) {
                x->parent = y;
            } else {
                transplant(y, y->right);
                y->right = z->right;
                y->right->parent = y;
            }

            transplant(z, y);
            y->left = z->left;
            y->left->parent = y;
            y->color = z->color;
        }

        delete z;  // 释放被删除节点内存

        // 若删除的是黑色节点，可能破坏红黑树性质，需要修复
        if (yOriginalColor == BLACK) {
            deleteFixup(x);
        }
    }

    // 查找节点（用于验证）
    bool search(int val) {
        Node* x = root;
        while (x != nil) {
            if (x->data == val) {
                return true;
            } else if (val < x->data) {
                x = x->left;
            } else {
                x = x->right;
            }
        }
        return false;
    }

    // 打印树结构
    void printTree() {
        inorderTraversal(root);
        cout << endl;
    }
};

// 测试红黑树删除功能
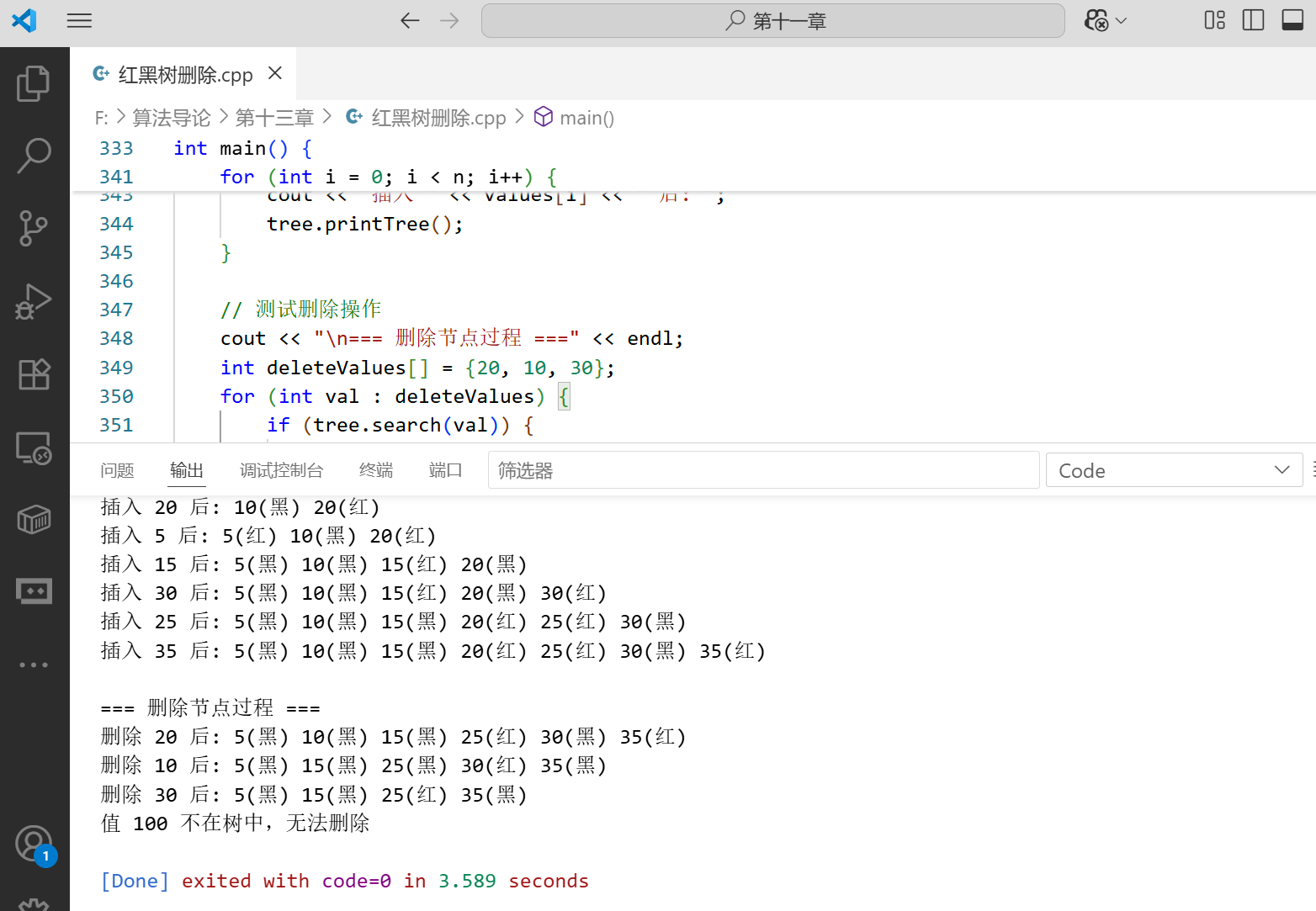
int main() {
    RedBlackTree tree;

    // 插入测试数据
    int values[] = {10, 20, 5, 15, 30, 25, 35};
    int n = sizeof(values) / sizeof(values[0]);

    cout << "=== 插入节点过程 ===" << endl;
    for (int i = 0; i < n; i++) {
        tree.insert(values[i]);
        cout << "插入 " << values[i] << " 后: ";
        tree.printTree();
    }

    // 测试删除操作
    cout << "\n=== 删除节点过程 ===" << endl;
    int deleteValues[] = {20, 10, 30};
    for (int val : deleteValues) {
        if (tree.search(val)) {
            tree.deleteNode(val);
            cout << "删除 " << val << " 后: ";
            tree.printTree();
        } else {
            cout << "删除 " << val << " 失败：节点不存在" << endl;
        }
    }

    // 测试删除不存在的节点
    tree.deleteNode(100);

    return 0;
}

综合案例：红黑树实现有序映射

以下是一个完整的红黑树应用案例，实现了有序映射的插入、删除、查找和遍历功能：

cpp 复制代码 
#include <iostream>
using namespace std;

// 节点颜色定义
enum Color { RED, BLACK };

// 红黑树节点结构
struct Node {
    int data;               // 节点值
    Color color;            // 节点颜色
    Node *left, *right, *parent;  // 左子、右子、父节点

    // 构造函数
    Node(int val) : data(val), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};

// 红黑树类
class RedBlackTree {
private:
    Node* root;
    Node* nil;  // 哨兵节点（简化边界处理）

    // 左旋操作
    void leftRotate(Node* x) {
        Node* y = x->right;
        x->right = y->left;

        if (y->left != nil) {
            y->left->parent = x;
        }

        y->parent = x->parent;

        if (x->parent == nil) {
            root = y;
        } else if (x == x->parent->left) {
            x->parent->left = y;
        } else {
            x->parent->right = y;
        }

        y->left = x;
        x->parent = y;
    }

    // 右旋操作
    void rightRotate(Node* y) {
        Node* x = y->left;
        y->left = x->right;

        if (x->right != nil) {
            x->right->parent = y;
        }

        x->parent = y->parent;

        if (y->parent == nil) {
            root = x;
        } else if (y == y->parent->right) {
            y->parent->right = x;
        } else {
            y->parent->left = x;
        }

        x->right = y;
        y->parent = x;
    }

    // 插入修复
    void insertFixup(Node* z) {
        while (z->parent->color == RED) {
            if (z->parent == z->parent->parent->left) {
                Node* y = z->parent->parent->right;
                if (y->color == RED) {
                    z->parent->color = BLACK;
                    y->color = BLACK;
                    z->parent->parent->color = RED;
                    z = z->parent->parent;
                } else {
                    if (z == z->parent->right) {
                        z = z->parent;
                        leftRotate(z);
                    }
                    z->parent->color = BLACK;
                    z->parent->parent->color = RED;
                    rightRotate(z->parent->parent);
                }
            } else {
                Node* y = z->parent->parent->left;
                if (y->color == RED) {
                    z->parent->color = BLACK;
                    y->color = BLACK;
                    z->parent->parent->color = RED;
                    z = z->parent->parent;
                } else {
                    if (z == z->parent->left) {
                        z = z->parent;
                        rightRotate(z);
                    }
                    z->parent->color = BLACK;
                    z->parent->parent->color = RED;
                    leftRotate(z->parent->parent);
                }
            }
        }
        root->color = BLACK;
    }

    // 移植节点（辅助删除）
    void transplant(Node* u, Node* v) {
        if (u->parent == nil) {
            root = v;
        } else if (u == u->parent->left) {
            u->parent->left = v;
        } else {
            u->parent->right = v;
        }
        v->parent = u->parent;
    }

    // 查找最小节点（找后继）
    Node* minimum(Node* x) {
        while (x->left != nil) {
            x = x->left;
        }
        return x;
    }

    // 删除修复
    void deleteFixup(Node* x) {
        while (x != root && x->color == BLACK) {
            if (x == x->parent->left) {
                Node* w = x->parent->right;
                if (w->color == RED) {
                    w->color = BLACK;
                    x->parent->color = RED;
                    leftRotate(x->parent);
                    w = x->parent->right;
                }

                if (w->left->color == BLACK && w->right->color == BLACK) {
                    w->color = RED;
                    x = x->parent;
                } else {
                    if (w->right->color == BLACK) {
                        w->left->color = BLACK;
                        w->color = RED;
                        rightRotate(w);
                        w = x->parent->right;
                    }
                    w->color = x->parent->color;
                    x->parent->color = BLACK;
                    w->right->color = BLACK;
                    leftRotate(x->parent);
                    x = root;
                }
            } else {
                Node* w = x->parent->left;
                if (w->color == RED) {
                    w->color = BLACK;
                    x->parent->color = RED;
                    rightRotate(x->parent);
                    w = x->parent->left;
                }

                if (w->right->color == BLACK && w->left->color == BLACK) {
                    w->color = RED;
                    x = x->parent;
                } else {
                    if (w->left->color == BLACK) {
                        w->right->color = BLACK;
                        w->color = RED;
                        leftRotate(w);
                        w = x->parent->left;
                    }
                    w->color = x->parent->color;
                    x->parent->color = BLACK;
                    w->left->color = BLACK;
                    rightRotate(x->parent);
                    x = root;
                }
            }
        }
        x->color = BLACK;
    }

    // 中序遍历（内部实现）
    void inorderTraversal(Node* x) {
        if (x != nil) {
            inorderTraversal(x->left);
            cout << x->data << "(" << (x->color == RED ? "红" : "黑") << ") ";
            inorderTraversal(x->right);
        }
    }

public:
    // 构造函数
    RedBlackTree() {
        nil = new Node(0);
        nil->color = BLACK;
        nil->left = nil;
        nil->right = nil;
        root = nil;
    }

    // 插入节点
    void insert(int val) {
        Node* z = new Node(val);
        Node* y = nil;
        Node* x = root;

        while (x != nil) {
            y = x;
            if (z->data < x->data) {
                x = x->left;
            } else {
                x = x->right;
            }
        }

        z->parent = y;
        if (y == nil) {
            root = z;
        } else if (z->data < y->data) {
            y->left = z;
        } else {
            y->right = z;
        }

        z->left = nil;
        z->right = nil;
        z->color = RED;

        insertFixup(z);
    }

    // 删除节点
    void deleteNode(int val) {
        Node* z = root;
        while (z != nil && z->data != val) {
            if (val < z->data) {
                z = z->left;
            } else {
                z = z->right;
            }
        }

        if (z == nil) {
            cout << "值 " << val << " 不在树中，无法删除" << endl;
            return;
        }

        Node* y = z;
        Color yOriginalColor = y->color;
        Node* x = nil;

        if (z->left == nil) {
            x = z->right;
            transplant(z, z->right);
        } else if (z->right == nil) {
            x = z->left;
            transplant(z, z->left);
        } else {
            y = minimum(z->right);
            yOriginalColor = y->color;
            x = y->right;

            if (y->parent == z) {
                x->parent = y;
            } else {
                transplant(y, y->right);
                y->right = z->right;
                y->right->parent = y;
            }

            transplant(z, y);
            y->left = z->left;
            y->left->parent = y;
            y->color = z->color;
        }

        delete z;

        if (yOriginalColor == BLACK) {
            deleteFixup(x);
        }
    }

    // 查找节点
    bool search(int val) {
        Node* x = root;
        while (x != nil) {
            if (x->data == val) {
                return true;  // 找到节点
            } else if (val < x->data) {
                x = x->left;  // 向左子树查找
            } else {
                x = x->right;  // 向右子树查找
            }
        }
        return false;  // 未找到节点
    }

    // 公开接口：打印树
    void printTree() {
        cout << "中序遍历（值+颜色）：";
        inorderTraversal(root);
        cout << endl;
    }
};

// 测试代码
int main() {
    RedBlackTree tree;

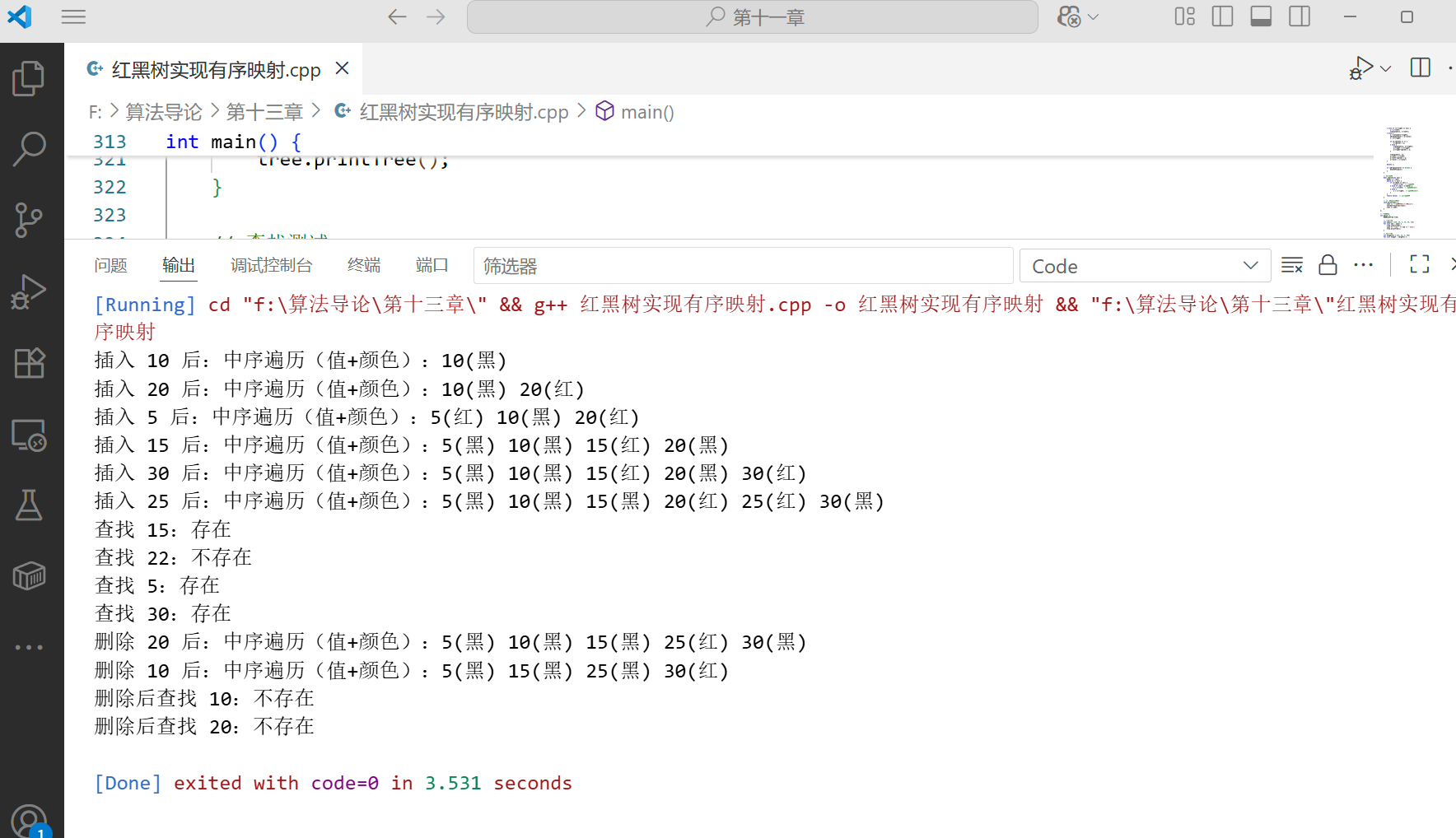
    // 插入测试
    int nums[] = {10, 20, 5, 15, 30, 25};
    for (int num : nums) {
        tree.insert(num);
        cout << "插入 " << num << " 后：";
        tree.printTree();
    }

    // 查找测试
    int targets[] = {15, 22, 5, 30};
    for (int target : targets) {
        cout << "查找 " << target << "：" << (tree.search(target) ? "存在" : "不存在") << endl;
    }

    // 删除测试
    tree.deleteNode(20);
    cout << "删除 20 后：";
    tree.printTree();

    tree.deleteNode(10);
    cout << "删除 10 后：";
    tree.printTree();

    // 验证删除后的查找结果
    cout << "删除后查找 10：" << (tree.search(10) ? "存在" : "不存在") << endl;
    cout << "删除后查找 20：" << (tree.search(20) ? "存在" : "不存在") << endl;

    return 0;
}

输出结果示例

思考题

  1. 证明红黑树的高度不超过 2log (n+1)（提示：利用黑高和二叉树高度的关系）。
  2. 若将新插入节点初始颜色设为黑色，会对红黑树性质产生什么影响？修复成本如何变化？
  3. 设计一个算法，统计红黑树中红色节点的数量，要求时间复杂度 O (n)。
  4. 比较红黑树与 AVL 树的优缺点及适用场景。

本章注记

  • 红黑树由 Rudolf Bayer 于 1972 年发明，最初称为 "对称二叉 B 树"，后由 Leo Guibas 和 Robert Sedgewick 简化并命名为红黑树。
  • 红黑树在工程中应用广泛：C++ STL 的std::map和std::set、Java 的TreeMap、Linux 内核的进程调度、nginx 的定时器等均采用红黑树实现。
  • 红黑树的平衡策略是 "宽松平衡"（黑高平衡），相比 AVL 树的 "严格平衡"（高度差≤1），插入删除的旋转次数更少，适合频繁修改的场景。
  • 红黑树的哨兵节点（nil）是工程实现中的常用技巧，可简化边界条件判断（如避免空指针检查）。

说明

本文提供的红黑树代码已包含所有核心功能（插入、删除、查找、遍历），可直接编译运行。代码采用哨兵节点简化逻辑，所有操作均保证红黑树性质不被破坏，时间复杂度为 O (log n)。实际使用时可根据需求扩展（如泛型支持、自定义比较器等）。

相关推荐
hn小菜鸡21 小时前
LeetCode 2460.对数组执行操作
算法·leetcode·职场和发展
.YM.Z21 小时前
数据结构——链表
数据结构·链表
jghhh0121 小时前
HT16C21 驱动模拟I2C实现
单片机·嵌入式硬件·算法
自信的小螺丝钉21 小时前
Leetcode 148. 排序链表 归并排序
算法·leetcode·链表·归并
listhi5201 天前
基于梯度下降、随机梯度下降和牛顿法的逻辑回归MATLAB实现
算法·matlab·逻辑回归
hhhwx6661 天前
Linux学习记录--利用信号量来调度共享资源（2）
linux·c语言·c++·学习
熊猫_豆豆1 天前
目前顶尖AI所用算法，包含的数学内容，详细列举
人工智能·算法
1白天的黑夜11 天前
队列+宽搜(BFS)-662.二叉树最大宽度-力扣(LeetCode)
c++·leetcode·宽度优先·队列
yihai-lin1 天前
Rust/C/C++ 混合构建 - Cmake集成Cargo编译动态库
c语言·c++·rust
野犬寒鸦1 天前
从零起步学习Redis || 第二章：Redis中数据类型的深层剖析讲解（下）
java·redis·后端·算法·哈希算法
热门推荐
01Multisim使用教程详尽版--(2025最新版)02UV 工具安装与国内镜像源配置指南03GitHub 镜像站点0446个Nano-banana 精选提示词，持续更新中05UV安装并设置国内源06Spec-Kit 使用指南07VsCode远程Copilot无法使用Claude Agent问题08保姆级教程：手把手教你用Dify实现完美多轮对话（附Chatflow和提示词）09KGG转MP3工具|非KGM文件|解密音频10Linux下V2Ray安装配置指南