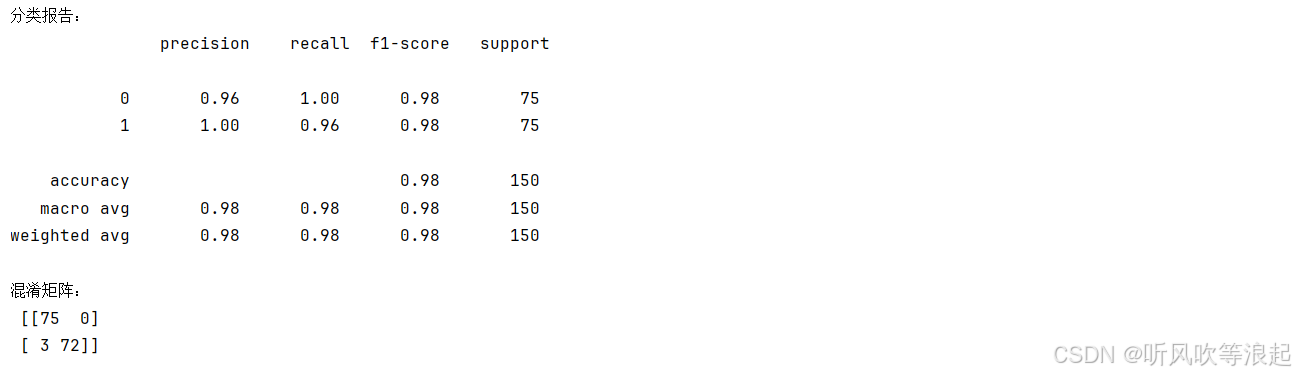分类算法：支持向量机

1.⽀持向量机是什么？

2.例子

[3.为什么 SVM 的分割线是最优的？](#3.为什么 SVM 的分割线是最优的？)

[4.SVM 优缺点对比](#4.SVM 优缺点对比)

[5.SVM 适用场景](#5.SVM 适用场景)

6.完整案例

今天我们来探讨机器学习分类算法中的支持向量机(SVM)。

首先简单介绍一下分类算法的概念。分类是机器学习中的一种重要任务，目的是根据数据的特征将其划分到预定义的类别中。举个例子，就像侦探破案时，通过分析鞋码和手套尺寸等特征，来判断一个人是成年人还是儿童，这就是典型的分类问题。

在所有分类算法中，支持向量机是一种非常重要且强大的模型。它通过寻找最优决策边界来实现分类，具有很好的泛化能力。接下来，我们将重点讨论这个算法的原理和应用。

1.⽀持向量机是什么？

支持向量机(SVM)的核心原理可以概括为以下两点关键思想：

最优分类边界：SVM致力于在特征空间中寻找一个最优的决策超平面（在二维情况下表现为一条直线），这个超平面能够最清晰地将不同类别的数据点分隔开来。
最大化间隔原则：这个决策边界不是随意确定的，而是通过最大化与最近数据点（即支持向量）的距离来确定的。这就像在网球场上分隔红球和蓝球时，我们选择的界线要确保离界线最近的红球和蓝球都尽可能远离这条分界线。

这种基于间隔最大化的方法赋予了SVM出色的泛化能力，使其对噪声数据具有较强的鲁棒性。支持向量（即距离决策边界最近的那些数据点）就像"球场边线上的球"一样，真正决定了边界的位置，而其他远离边界的点则不会影响最终的决策边界。

2.例子

数据示例（判断标准：鞋子和手套尺寸）

鞋子大小 (x₁)	手套大小 (x₂)	类别
8	7	小孩
9	8	小孩
12	10	成年人
13	11	成年人

目标：

找到一个最佳的分界线（决策边界），能够准确地区分「成年人」和「小孩」。

SVM 的工作方式：

寻找最优分界线：
- 在二维平面上（x₁=鞋子大小，x₂=手套大小），SVM 会尝试画一条直线（比如：x₂ = 0.8x₁ + 1），使得这条线能够最好地分开两类数据。
- 这条线不仅要能正确分类，还要尽可能远离两边的数据点，提高模型的鲁棒性。
支持向量的作用：
- 假设最近的分界线的点是：
  - 小孩类：(9, 8)
  - 成年人类：(12, 10)
- 这些点就是支持向量，它们决定了最终的决策边界。
- SVM 会调整分界线，使得它到 (9, 8) 和 (12, 10) 的距离最大化。
分类新数据：
- 如果来了一个新数据（鞋子=11，手套=9），SVM 会根据它落在分界线的哪一侧来判断是「成年人」还是「小孩」。

直观理解：

就像在足球场上，裁判要在两队球员之间画一条中线，使得这条线离双方最近的球员（支持向量）尽可能远，避免误判。
SVM 的决策边界不是随便画的，而是最公平、最稳健的那条线！

这样，即使未来有稍微偏差的数据（比如一个脚稍大的小孩），模型也能正确分类。 🚀

3.为什么 SVM 的分割线是最优的？

SVM（支持向量机）的分割线之所以被称为"最优"，是因为它不仅仅满足于简单分开数据，而是通过数学优化确保：

1. 最大化间隔（Margin Maximization）

SVM 的分割线会尽量远离两侧的数据点，而不是紧贴着某一类。
为什么？ 这样即使新数据有轻微偏差（比如测量误差），模型仍然能正确分类，提高泛化能力。
类比：就像在马路上画车道线，最优的线应该让两边的车都有足够的行驶空间，而不是紧贴某一侧。

2. 支持向量决定边界（Support Vectors Matter）

只有离分割线最近的点（支持向量） 会影响最终的分割线位置，其他远处的点不影响。
为什么？ 这些关键点就像"边界守卫"，决定了模型的鲁棒性。如果它们移动，分割线也会跟着调整。
类比：足球场上的边界线由最靠近它的球员决定，其他远处的球员不影响界线位置。

3. 数学优化保证全局最优

SVM 通过求解一个凸优化问题 （如最大化间隔 Margin = 2 / ||w||），确保找到的分割线是唯一最优解，不会陷入局部最优。
为什么？ 传统方法（如逻辑回归）可能找到多个可行的分割线，但 SVM 保证找到最健壮的那一条。

总结 SVM 的 3 大核心优势

分类的本质是找规律
- 就像侦探根据"鞋子大小"和"手套大小"判断成人/小孩，SVM 通过数据特征找到分类规律。
SVM 的分割线是"最优"的
- 不是随便画一条线，而是让两边的数据尽可能远离它（最大化间隔），提高模型的稳定性。
新数据预测简单高效
- 判断新样本时，只需看它在分割线的哪一侧，计算速度快，适合实际应用。

最终结论

SVM 的"最优分割线"之所以强，是因为它：

✅ 最大化间隔 → 提高泛化能力，防止过拟合

✅ 仅依赖支持向量 → 计算高效，抗噪声干扰

✅ 数学保证全局最优 → 不像神经网络可能陷入局部最优

这使得 SVM 特别适合小样本、高维度的分类问题（如文本分类、生物医学数据等）。 🚀

4.SVM 优缺点对比

类别	说明
优点
1. 高维有效性	在特征维度高于样本量时仍有效（如文本分类、基因数据）
2. 非线性能力	通过核函数（RBF/多项式）处理复杂边界，无需手动特征工程
3. 抗过拟合	最大化间隔原则提升泛化能力
4. 鲁棒性	仅依赖支持向量，对噪声和离群点不敏感
5. 参数简洁	主要调参仅`C`（正则化）和核参数（如`γ`）
缺点
1. 计算成本高	训练复杂度O(n²)~O(n³)，百万级数据难以应用
2. 参数敏感	`C`和核参数选择对结果影响大，需网格搜索
3. 类别不平衡	需人工调整类权重或采样，否则偏向多数类
4. 黑箱性	核变换后的决策逻辑难以解释（与决策树对比）
5. 内存限制	需存储核矩阵，大数据场景内存消耗显著

5.SVM 适用场景

场景	典型案例	原因
1. 文本分类	垃圾邮件识别、情感分析	高维稀疏特征（TF-IDF）下表现优异
2. 小样本图像分类	手写数字识别（MNIST）	核函数可捕捉像素间非线性关系
3. 生物信息学	基因表达数据分类	样本少（~100）、特征多（~万级基因）的理想场景
4. 金融风控	信用卡欺诈检测	对异常值（欺诈样本）鲁棒性强
5. 医学诊断	肿瘤良恶性判断（乳腺癌数据集）	小样本高维数据中保持较高准确率
6. 时序数据分类	ECG心律失常检测	RBF核可建模时序动态模式
不适用场景
1. 超大规模数据	互联网广告点击预测	计算资源需求过高，推荐用随机森林/深度学习
2. 实时性要求高的系统	自动驾驶实时物体检测	推理速度慢于轻量级模型（如MobileNet）
3. 需要可解释性的领域	金融监管合规报告	核函数变换后的特征无明确业务意义

参数选择建议

线性可分数据
- 核函数：线性核（kernel='linear'）
- 调参重点：正则化参数C（典型值0.1~10）
非线性数据
- 核函数：RBF核（kernel='rbf'）
- 调参重点：C + gamma（γ控制决策边界弯曲度）
类别不平衡
- 使用class_weight='balanced'自动调整类别权重

与其他模型对比

模型	适合场景	相对SVM的优势
随机森林	大规模数据、特征交互复杂	训练更快、更易调参
逻辑回归	线性问题、需概率输出	计算效率高、可解释性强
神经网络	超大规模非线性数据	自动特征提取、端到端学习

通过此总结可快速判断SVM是否适合当前任务，并指导参数调优和替代方案选择。

6.完整案例

下面演示了如何使用支持向量机(SVM)对非线性数据集进行分类。以下是代码的主要功能和步骤：

数据集生成：
- 使用make_moons生成500个样本的"月亮形"非线性可分数据集，添加了0.2的噪声
数据划分：
- 将数据集按7:3的比例划分为训练集和测试集
模型训练：
- 创建SVM分类器，使用RBF(径向基函数)核函数
- 设置正则化参数C=1.0，gamma='scale'(自动缩放)
模型评估：
- 在测试集上进行预测
- 输出分类报告(精确度、召回率、F1分数等)
- 输出混淆矩阵
可视化：
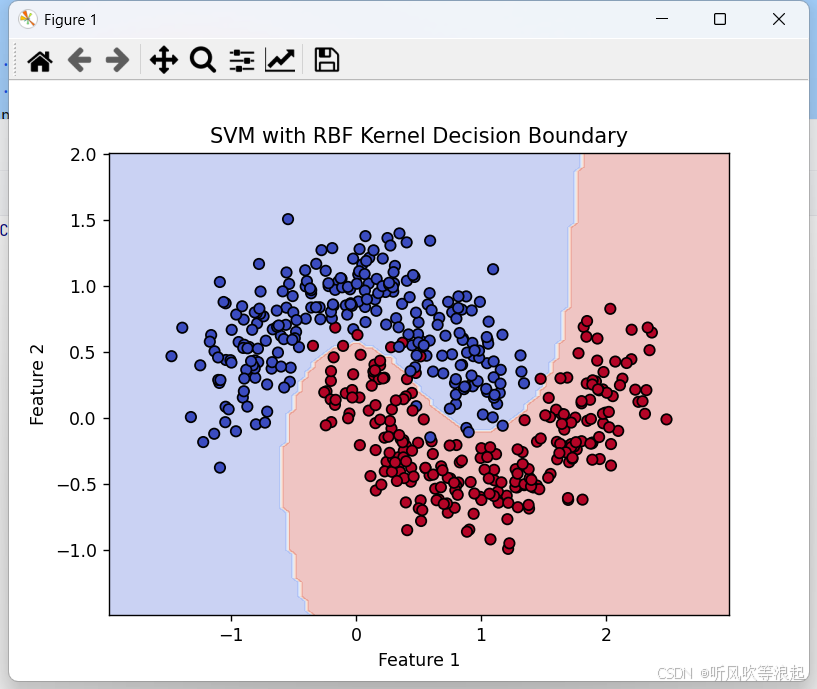
- 绘制决策边界和原始数据点的散点图
- 使用不同颜色区分两个类别

这段代码展示了SVM处理非线性分类问题的能力，RBF核函数能够很好地拟合这种复杂形状的决策边界。可视化部分直观地显示了模型如何将两个"月亮形"的类别分开。

python 复制代码

# 导入必要库
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix

# 1. 生成非线性数据集（ moons 数据集）
X, y = datasets.make_moons(n_samples=500, noise=0.2, random_state=42)

# 2. 划分训练集/测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 3. 训练SVM模型（使用RBF核）
svm = SVC(kernel='rbf', C=1.0, gamma='scale', random_state=42)
svm.fit(X_train, y_train)

# 4. 评估模型
y_pred = svm.predict(X_test)
print("分类报告：\n", classification_report(y_test, y_pred))
print("混淆矩阵：\n", confusion_matrix(y_test, y_pred))


# 5. 可视化决策边界
def plot_decision_boundary():
    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
                         np.linspace(y_min, y_max, 100))
    Z = svm.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)

    plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm)
    plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.coolwarm)
    plt.title("SVM with RBF Kernel Decision Boundary")
    plt.xlabel("Feature 1")
    plt.ylabel("Feature 2")
    plt.show()


plot_decision_boundary()