注意:1、核函数的选择成为支持向量机最大的变数,支持向量机需要在当前空间中线性可分且当前空间的好坏对这个算法的性能有很大影响,因此核函数的选择是svm中非常重要的。
2、现实任务中,很难找到一个核函数使得训练样本在映射到的特征空间中线性可分。
思想:对于硬间隔的svm思想是在特征空间中找到最优超平面,使得最大化分类间隔,同时可以利用核技巧处理非线性问题,也就是说硬间隔的svm不允许有样本点分类错误。对于软间隔的svm思想是在特征空间中找到最优超平面,使得对分类正确的样本点最大化分类间隔并且最小化所有分类错误的样本点到超平面的距离之和,它的想法是这样,最终的目标函数给最小化所有分类错误的样本点到超平面的距离之和赋予一个系数C,来表示后者的重要程度,如果C无穷大则表示要将所有样本分类正确,C相等于超参数。
涉及的知识:核函数,拉格朗日乘子法,点到平面的距离公式,
核心内容:1、支持向量:决定最优超平面的只有距离超平面最近的少数样本点,这些点就是 "支持向量"------ 其他样本点的位置不影响超平面的位置。
2、软间隔:现实中数据往往线性不可分,SVM 引入 "软间隔"(允许部分样本点落在间隔内甚至超平面另一侧),同时通过惩罚项控制错误样本的数量,平衡间隔大小与分类错误。
优点:1、适合高维数据。即使特征维度远大于样本数量,也能有效学习(因为依赖支持向量而非全部样本)。
缺点:1、多分类支持差。原生 SVM 是二分类模型,处理多分类需要间接方法(如一对一、一对多),效率较低。
2、对核函数敏感。
西瓜书的支持向量机叙述顺序
因为有的论文需要搞明白支持向量机如何推导出来的才能看明白论文,因此在此我将西瓜书的叙述顺序记录下来。这里不需要搞懂式子怎么推出来的,只需要知道推导顺序即可,如果想知道怎样推导出来的可以看对应的南瓜书。
叙述中的相关式子见下图。
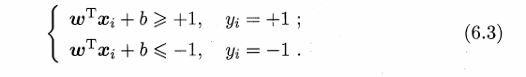
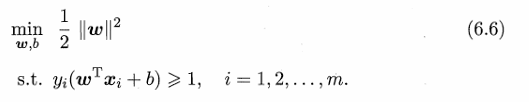
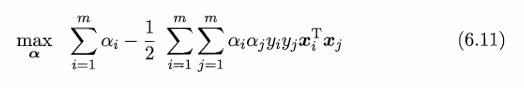
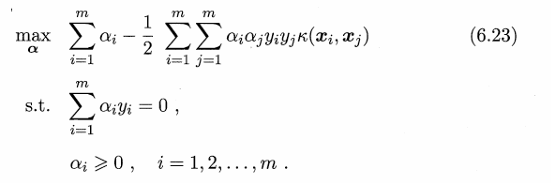

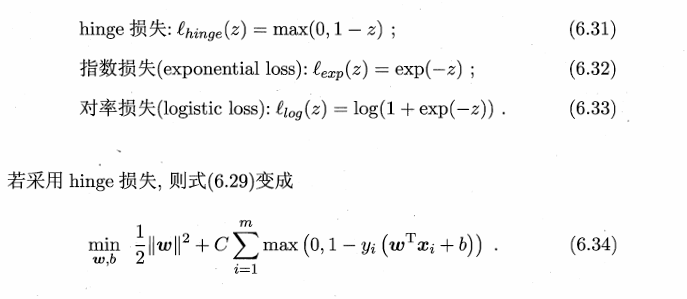

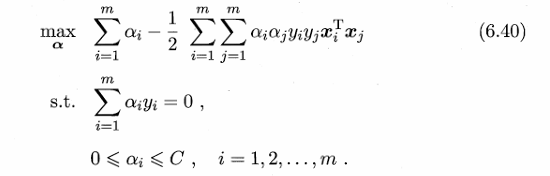
硬间隔的支持向量机所要求的超平面需要满足三个条件,第一个是能正确划分正负样本,第二个是要位于正负样本正中间,第三个是离正负样本都尽可能远。要想满足前两个条件就需要满足6.3式,也即6.6式中的下面那个式子,要想满足三个条件就需要满足6.6式,6.6式和6.11式是强对偶问题,所以求解6.6式等价于求解6.11式。如果当前特征空间线性不可分就需要用到核函数,引入核函数之后6.11式就变成了6.23式。也就是说硬间隔的支持向量机的目标函数是6.23式。
软间隔的支持向量机需要满足6.29式,但是6.29式用到了0/1损失函数,而它的数学性质不好,常用hinge损失、指数损失和对率损失来替代它,西瓜书用的hinge损失替代,这样就得到了6.34式,然后就可以推导出6.35式,6.35式和6.40式是强对偶问题,因此求解6.35式等价于求解6.40式,引入核函数之后就6.40式就变成了下图的式子。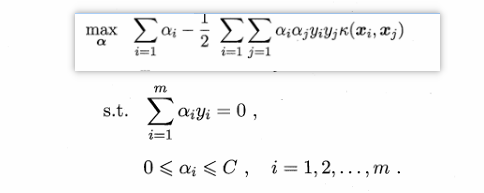
相应的还有支持向量回归(SVR),待更新。
核函数
核函数的定义


常见的核函数

核函数导出核函数的方法
