Day 96
题目描述

思路
对于乘法出现低位0,只有可能由以下可能
- 一个偶数乘以5
- 任何数乘以一个末尾为0的数
基于以上这两点,我们可以找到一个共同特征,及找到阶乘中能被5整除的数 ,
但是这里又出现一个问题:
254可以得到2个0,25 2只能得到一个0,我们需要统一,不然还是无法统计,
但是我们直到25可以表示为5*5,对于任何能被5整除的数表示为若干个5乘某个数 ,
这样我们就只统计5的个数
java
class Solution {
public int trailingZeroes(int n) {
if(n==0){
return 0;
}
int sum=0;
for(int i=1;i<=n;i++){
if(i%5==0&&i!=0){
int x=i;
while(x%5==0){
x=x/5;
sum++;
}
}
}
return sum;
}
}题目描述
思路
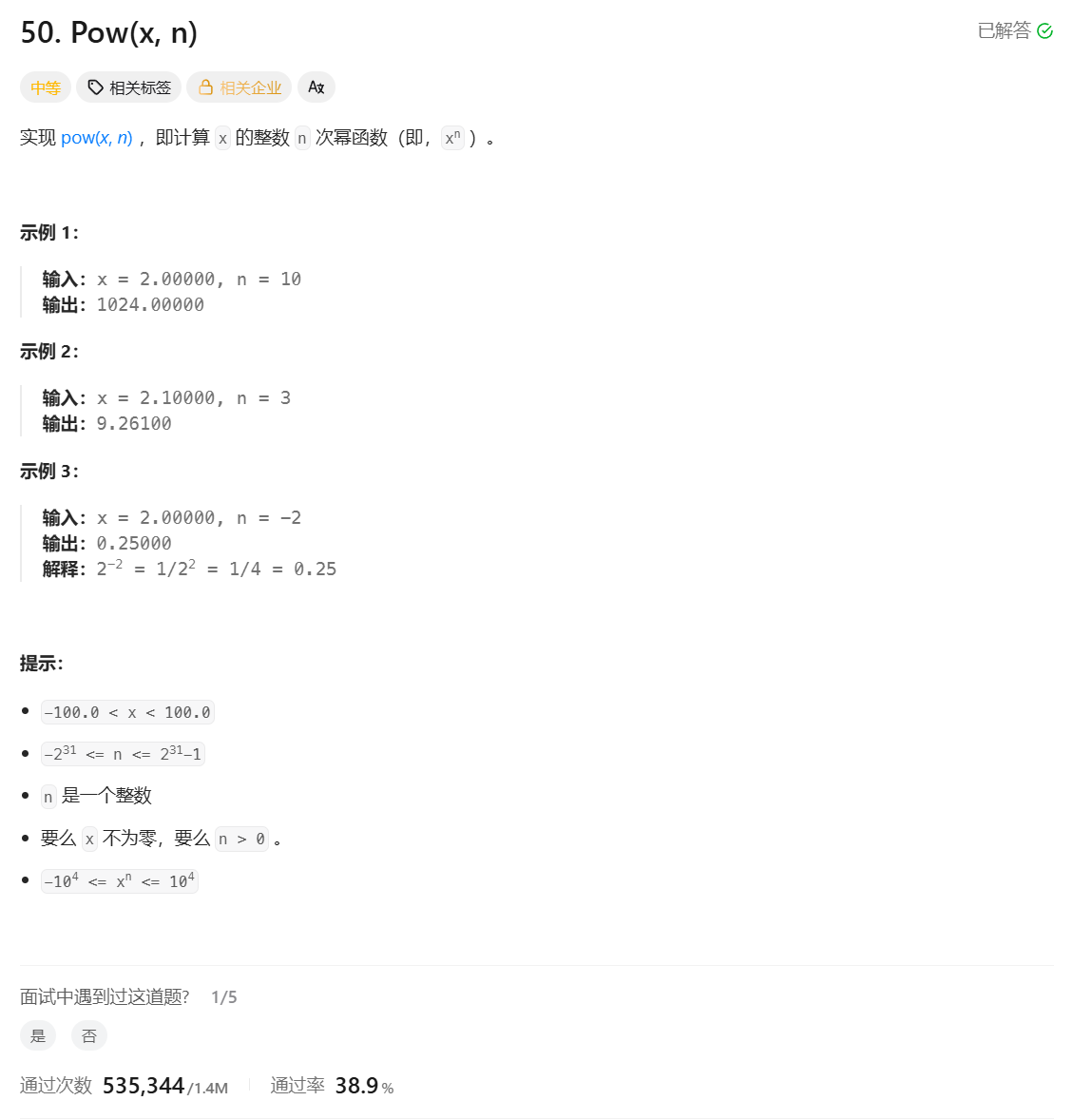
**递归思路:**这题一看数据就知道不能直接采取循环,因为次数达到了2的31-1的数量级,那我们换个思路(我们只考虑正的情况 ):
我们取x的平方来做,是不是整体的次数会被除2,这样就降低了数量级
我们再取x的四次方来做,这样数量级是不是降低的更多
但是这里会出现问题,比如我们采取4次方,他可能会超过规定的次数,可能超出1 2 3个 这种情况就会很麻烦 ,有没有更方便的做法。
我选择每次都去数值的平方,这样可能出现的情况无非就是超出一个,那么可以在递归中判断,
如果次数能被2整除,就直接取平方,次数除2 即可
如果不能被2整除,也取平方,次数除2,但是我们需要补一个x,原因在于/2是取小的,加一个x保证数值正确即可
java
class Solution {
public double find(double x,int n){
if(n==1||n==0){
return x;
}
if(n%2==0){
return find(x*x,n/2);
}
return find(x*x,n/2)*x;
}
public double myPow(double x, int n) {
if(n==0){
return 1;
}
if(n<0){//转化为正数
x=1/x;
n=n*-1;
}
return find(x,n);
}
}题目描述
思路
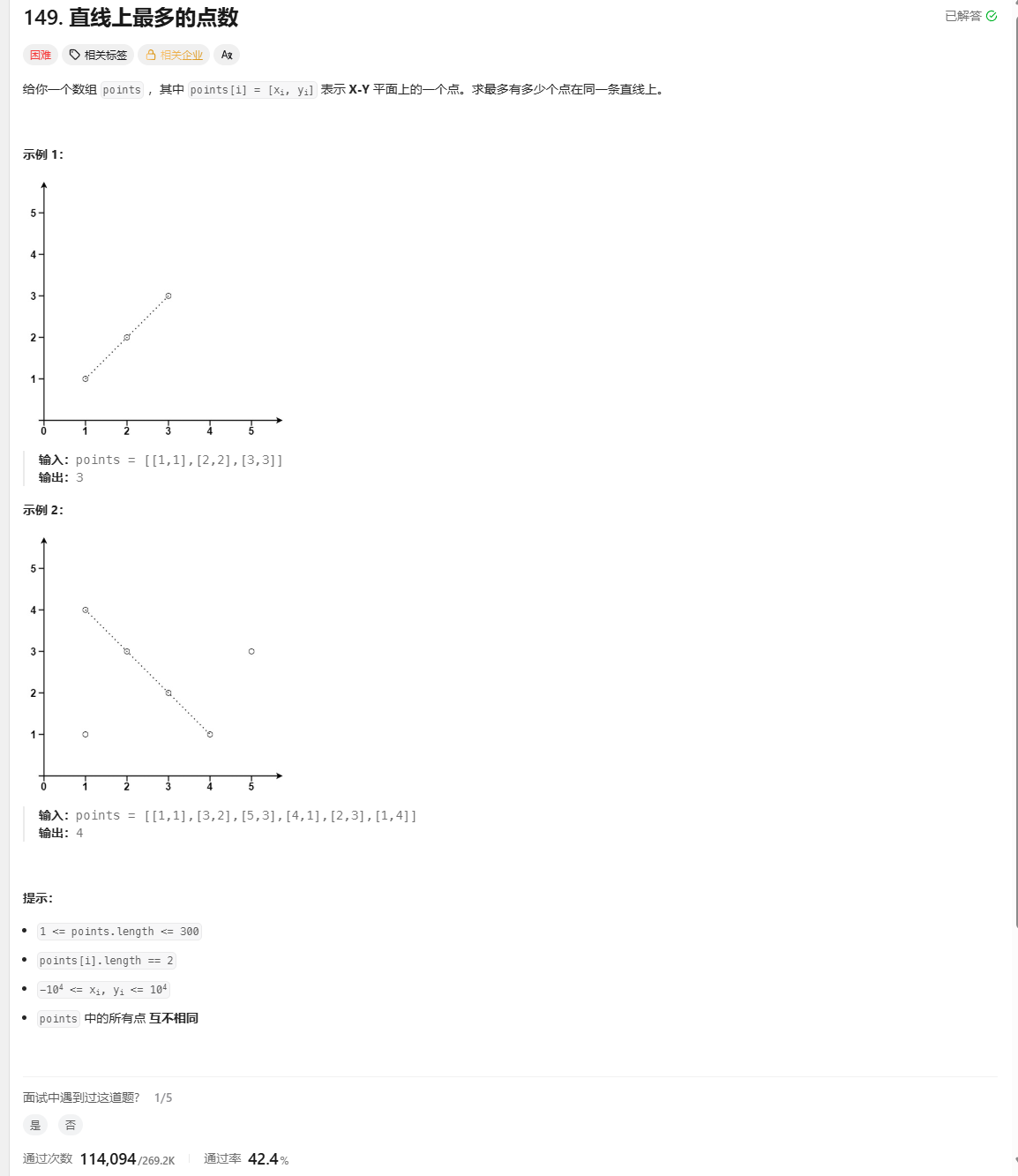
初次思路 :众所周知,两个点确定一条直线,这题最关键的点在于必须减少计算点与点的直线的次数,如果说,两个点连成一条直线,其中经过的其余点任意取两点只能同时在这根线上,这就是解题的关键
- 我们去一个hash数组来保存点与点之间是否已经同时在一条计算过的直线上
- 进入循环,我取两个点
- 首先判断这两个点是否在hash中已经共存一条线上
- 存在就不算了 下一个
- 不存在,就通过kx+b确定一条直线,遍历数组判断是否还有其余点在这个线上
- 在就在hash表中记录下
- 比较个数,更新max
需要额外注意的点
-
kx+b可能k和b不是整数,我们采取做差判断误差来防止出现精度的问题
-
可能出现一条竖的线,不能使用kx+b表示,特殊处理。
java
class Solution {
public int check(int[][]hash,int[][]points,double k,double b,int m){
int sum=0;
List<Integer>res=new ArrayList<>();
for(int i=0;i<points.length;i++){
int x=points[i][0];
int y=points[i][1];
if(m==-1){
double tes=(k*x+b)-(double)y;
if(Math.abs(tes)<0.00001){
sum++;
res.add(i);
}
}
else{
if(x==m){
sum++;
res.add(i);
}
}
}
for(int i=0;i<res.size();i++){
for(int j=0;j<res.size();j++){
hash[res.get(i)][res.get(j)]=1;
}
}
return sum;
}
public int maxPoints(int[][] points) {
int n=points.length;
int[][]hash=new int[n][n];
int max=1;
for(int s=0;s<n;s++){
int x=points[s][0];
int y=points[s][1];
for(int i=s;i<n;i++){
int x1=points[i][0];
int y1=points[i][1];
if(hash[s][i]==1){//说明这条直线之前确定过
}
else{//确定一条直线(kx+b=y)
double k,b;
k=x1-x;
double p=y1-y;
if(k==0){//一条横线y=b
b=p;
}
else{
k=p/k;
b=y-k*x;
}
int sum=0;
if(x1==x&&y!=y1){//一条竖线
sum=check(hash,points,k,b,x);
}
else{
sum=check(hash,points,k,b,-1);
}
if(sum>max){
max=sum;
}
}
}
}
return max;
}
}题解做法
核心逻辑 :固定一个点i,计算其他所有点j与i形成的直线斜率,通过哈希表统计「相同斜率」的点数量(斜率相同意味着共线),最终取最大值。
斜率处理 :用「分数最简形式」表示斜率(通过最大公约数 GCD 化简),避免浮点数精度误差。例如,斜率 2/4 会化简为 1/2,用(x,y)=(1,2)表示,再通过key = y + x * 20001生成唯一标识。
优化策略:当当前最大值已足够大(如ret >= n - i)时提前退出循环,减少无效计算。
java
class Solution {
public int maxPoints(int[][] points) {
int n = points.length;
// 边界情况:0/1/2个点,直接返回点的数量(必然共线)
if (n <= 2) {
return n;
}
int ret = 0; // 记录全局最大共线点数量
// 外层循环:固定基准点i
for (int i = 0; i < n; i++) {
// 优化1:如果当前最大值已足够大,提前退出
// 原因:剩余点(n-i个)即使全和i共线,总数也不会超过ret,无需继续计算
if (ret >= n - i || ret > n / 2) {
break;
}
// 哈希表:key=斜率的唯一标识,value=该斜率对应的点数量(不含基准点i)
Map<Integer, Integer> map = new HashMap<>();
// 内层循环:计算其他点j与基准点i的斜率
for (int j = i + 1; j < n; j++) {
// 计算两点的x差和y差(Δx = x_i - x_j,Δy = y_i - y_j)
int x = points[i][0] - points[j][0];
int y = points[i][1] - points[j][1];
// 关键:将斜率用「最简分数」表示,避免浮点数精度误差
if (x == 0) {
// 竖线(x差为0):统一用y=1表示斜率(所有竖线斜率相同)
y = 1;
} else if (y == 0) {
// 水平线(y差为0):统一用x=1表示斜率(所有水平线斜率相同)
x = 1;
} else {
// 普通直线:化简分数Δy/Δx
if (y < 0) {
// 保证y为正数(统一表示,避免斜率2/-3和-2/3被视为不同)
x = -x;
y = -y;
}
// 计算最大公约数,化简分数
int gcdXY = gcd(Math.abs(x), Math.abs(y));
x /= gcdXY;
y /= gcdXY;
}
// 生成斜率的唯一标识key(避免哈希冲突)
// 原理:x和y的范围在[-10000,10000],用x*20001 + y确保唯一
int key = y + x * 20001;
// 更新哈希表:该斜率对应的点数量+1
map.put(key, map.getOrDefault(key, 0) + 1);
}
// 计算当前基准点i对应的最大共线点数量
int maxn = 0;
for (int num : map.values()) {
// 共线点数量 = 相同斜率的点数量 + 基准点i本身
maxn = Math.max(maxn, num + 1);
}
// 更新全局最大值
ret = Math.max(ret, maxn);
}
return ret;
}
// 辅助函数:计算两个数的最大公约数(用于化简分数)
public int gcd(int a, int b) {
return b != 0 ? gcd(b, a % b) : a;
}
}