「ECG信号处理——（23）基于ECG和PPG信号的血压预测」2025年8月12日

目录

1、引言

2、理论基础

（一）ECG和PPG信号与血压的关系

（二）卷积神经网络（CNN）原理

3、数据预处理原理

[3.1 信号同步与采样率统一](#3.1 信号同步与采样率统一)

[3.2 去噪滤波](#3.2 去噪滤波)

[3.3 信号归一化](#3.3 信号归一化)

[3.4 窗口切分公式](#3.4 窗口切分公式)

4、特征提取

[5. CNN 模型结构与原理](#5. CNN 模型结构与原理)

[5.1 模型设计思路](#5.1 模型设计思路)

[5.2 模型结构表](#5.2 模型结构表)

[6. 模型训练与参数设置](#6. 模型训练与参数设置)

[6.1 数据划分](#6.1 数据划分)

[6.2 优化器](#6.2 优化器)

[6.3 损失函数](#6.3 损失函数)

[6.4 批量与迭代设置](#6.4 批量与迭代设置)

[6.5 学习率调度](#6.5 学习率调度)

[6.6 正则化与防过拟合](#6.6 正则化与防过拟合)

[7. 实验结果与分析](#7. 实验结果与分析)

[7.1 评估指标](#7.1 评估指标)

[7.2 三种输入模式结果对比](#7.2 三种输入模式结果对比)

---

1、引言

本研究旨在开发一种基于卷积神经网络（CNN）的无创血压预测模型，利用可穿戴设备采集的ECG（心电图）和PPG（光电容积脉搏波）信号，实现对收缩压（SBP）、舒张压（DBP）和平均动脉压（MAP）的准确预测。通过数据预处理、特征提取、模型训练与评估等步骤，验证了融合ECG和PPG信号特征的模型在血压预测任务中的有效性。

高血压是全球最主要的心血管疾病风险因素之一，持续、无创、实时的血压监测对疾病预防与治疗至关重要。传统袖带式血压测量方法虽然准确，但无法实现连续监测；而基于生理信号（如心电 ECG、光电容积脉搏波 PPG）的预测方法，能够在不干扰被测者正常活动的情况下实现 连续、无创血压估计。

ECG 和 PPG 信号分别反映了：

• ECG（Electrocardiogram）：心脏电活动过程。

• PPG（Photoplethysmogram）：血管容积随心动周期变化的光学响应。

两者结合，可以捕捉到脉搏传导时间（PTT）、脉搏波形变化等与血压高度相关的特征。

2、理论基础

（一）ECG和PPG信号与血压的关系

ECG信号反映了心脏电活动的变化，与心脏的收缩和舒张过程密切相关。PPG信号则反映了血液体积的变化，与动脉脉搏的传播和血管的弹性特性相关。研究表明，ECG和PPG信号中蕴含的特征参数与血压水平存在一定的相关性。

（二）卷积神经网络（CNN）原理

CNN是一种专门用于处理具有网格结构数据（如图像、时间序列）的深度学习模型。其核心思想是通过卷积层自动提取数据中的局部特征，并通过池化层降低特征维度，减少计算量。CNN具有以下特点：

• 局部感知：卷积核只与输入数据的局部区域相连，能够捕捉局部特征。

• 参数共享：同一个卷积核在不同位置共享参数，减少了模型的参数量。

• 多层结构：通过堆叠多个卷积层和池化层，能够逐层提取更抽象的特征。

CNN的基本结构包括输入层、卷积层、池化层、全连接层和输出层。在血压预测任务中，CNN可以自动从ECG和PPG信号中提取特征，并将其映射到血压值空间。

3、数据预处理原理

信号预处理是血压预测模型的核心前置步骤，直接决定特征的可分性与模型训练的稳定性。本项目的数据预处理分为信号同步 → 去噪 → 标准化 → 分窗四个阶段。

3.1 信号同步与采样率统一

不同采集通道可能存在采样率和起始时间差异。例如：

• ECG 采样率可能为 500 Hz

• PPG 采样率可能为 125 Hz

• 血压标签通常以 1 Hz 或事件触发方式给出

为了确保两路信号在时间维度上一一对应 ，我们采用线性插值 + 重采样方法，将所有信号统一到 100 Hz 采样率。

线性插值公式：

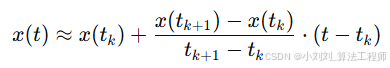
在两个已知采样点 t_kt和t_{k+1}之间，通过直线拟合的方式估算中间时刻 ttt 的信号值。

其中：

• x(t)：时刻 t 的信号幅值（插值结果）

• x(t_k)：采样点 t_k 的信号幅值

• x(t_{k+1})：采样点 t_{k+1}​ 的信号幅值

• t_k, t_{k+1}​：相邻两个采样点的时间

• t：需要插值的目标时间（位于t_k与t_{k+1}​之间）

这样可确保：（1）ECG、PPG、标签严格对齐；（2）消除采样不一致导致的时间漂移。

3.2 去噪滤波

信号中包含基线漂移、肌电干扰（EMG）、工频噪声等，若直接输入模型会显著降低预测精度，所以需要对信号进行去噪滤波处理，相关内容如下所述。

滤波策略：

（1）ECG（0.5--40 Hz 带通滤波）

• 下限 0.5 Hz 去除基线漂移（呼吸、姿势变化引起）

• 上限 40 Hz 去除高频噪声（EMG、工频）

IIR 带通滤波器传递函数：

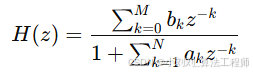
描述数字滤波器的输入与输出关系，用于从信号中保留特定频率范围（例如 0.5--40 Hz），并抑制其他频率。

其中：

• H(z)：滤波器在 z 域的传递函数

• b_k：分子系数（控制输入信号的加权方式）

• a_k​：分母系数（控制反馈部分的权重）

• M, N：滤波器分子和分母的阶数

• z^{-k}：延时 k 个采样点的操作

（2）PPG（0.5--20 Hz 低通滤波）

• 上限 20 Hz 保留主要脉搏波形

• 去除运动伪影与高频干扰

（3）抗混叠滤波

在重采样前加入低通滤波，防止高频成分折叠进低频信号。

3.3 信号归一化

不同受试者的信号幅值差异明显（与皮肤颜色、血流量、接触压力等有关），需要归一化到均值 0、方差 1：

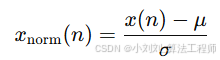
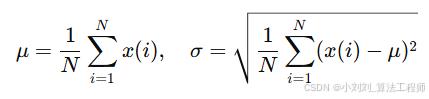
将信号缩放到均值为 0、标准差为 1 的分布，减少个体差异影响。

其中：

• x_norm​(n)：归一化后的第 n 个采样点值

• x(n)：原始信号第 n 个采样点值

• μ：原始信号的均值

• σ：原始信号的标准差

• N：总采样点数

3.4 窗口切分公式

为捕捉短时动态特征，将信号分为固定长度的滑动窗：

• 窗长 Tw=4 sT_w = 4 \ \text{s}Tw​=4 s，采样率 100 Hz → 每窗 400 点

• 步长 = 1 窗（无重叠），也可设置重叠提高样本量

窗口切分公式：

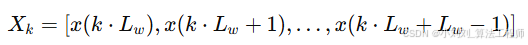
将长序列按固定长度 L_w切成一段段小片（窗口），供模型处理。这样每个窗口既保留完整一个或多个心动周期，又保证模型输入维度一致。

其中：

• Xk​：第 k 个时间窗口的信号片段

• x(⋅)：原始信号

• L_w：窗口长度（采样点数）

• k：窗口编号（从 0 开始）

4、特征提取

• 时域特征：

  • 均值（Mean）：反映信号的平均幅度。

  • 标准差（Standard Deviation）：衡量信号的离散程度。

  • 方差（Variance）：表示信号的波动程度。

  • 峰峰值（Peak-to-Peak）：信号的最大值与最小值之差。

  • 均方根值（RMS）：衡量信号的有效幅度。

  • 偏度（Skewness）：描述信号分布的对称性。

  • 峰度（Kurtosis）：反映信号分布的尖峭程度。

• 频域特征：

  • 平均功率（Mean Power）：信号在频域中的平均能量。

  • 中位功率（Median Power）：信号功率的中位值。

  • 最大功率（Maximum Power）：信号在某个频率下的最大能量。

  • 香农熵（Shannon Entropy）：衡量信号的复杂度。

5. CNN 模型结构与原理

CNN（卷积神经网络）可以自动从信号中提取局部模式（如 QRS 波、脉搏波上升沿等），无需人工设计特征。本项目采用一维卷积网络 （1D-CNN），输入为时间序列张量。

5.1 模型设计思路

1. 浅层卷积：提取局部波形变化（如心动周期形态）

2. 深层卷积：组合低层特征形成高层抽象模式

3. 全局平均池化（GAP）：直接将时序特征压缩为全局特征向量

4. 全连接层：完成回归预测（SBP、DBP）

5.2 模型结构表

表1：CNN网络模型结构

层名称	类型	参数设置	输出维度	功能说明
Input	输入层	shape=(400, C)	(400, C)	C 为通道数（1=单模态，2=融合）
Conv1	1D 卷积	filters=32, kernel=7, stride=1, padding=same	(400, 32)	提取局部时间相关特征
BN1	批标准化	-	(400, 32)	稳定梯度，减少内部协变量偏移
ReLU1	激活	ReLU	(400, 32)	增加非线性
MaxPool1	最大池化	pool=2	(200, 32)	降低时间分辨率
Conv2	1D 卷积	filters=64, kernel=5	(200, 64)	更深层的模式提取
BN2	批标准化	-	(200, 64)	稳定训练
ReLU2	激活	ReLU	(200, 64)	非线性特征映射
MaxPool2	最大池化	pool=2	(100, 64)	降低序列长度
Conv3	1D 卷积	filters=128, kernel=3	(100, 128)	高阶时间特征提取
BN3	批标准化	-	(100, 128)	-
ReLU3	激活	ReLU	(100, 128)	-
GAP	全局平均池化	-	(128,)	压缩时序维度，保留全局信息
Dense1	全连接	units=64	(64,)	融合全局特征
Dropout	随机失活	rate=0.5	(64,)	防止过拟合
Output	全连接	units=2	(2,)	输出 SBP 与 DBP 预测值

6. 模型训练与参数设置

6.1 数据划分

• 训练集：70%

• 验证集：15%

• 测试集：15%

6.2优化器

采用 Adam（Adaptive Moment Estimation）：

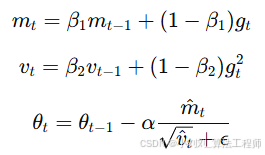
Adam 是一种结合了动量法和自适应学习率的梯度下降优化方法，可加快收敛并减少震荡。

其中：

• m_t​：梯度一阶矩（类似动量）

• v_t：梯度二阶矩（类似 RMSProp 的平方梯度均值）

• g_t​：当前梯度

• β1,β2：衰减系数，控制历史梯度的影响（典型值 0.9 和 0.999）

• α：学习率取1×10^{-3}

• ϵ：防止除零的微小数取1×10^{-8}

• θ_t：第 ttt 次迭代的模型参数

• hat{m}_t, hat{v}_t：偏差修正后的一阶、二阶矩

6.3损失函数

采用 均方误差（MSE）

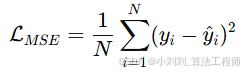
MSE 对大误差更敏感，适合回归任务。

其中：

• N：样本数

• y_i：第 i 个样本的真实值

• hat{y}_i​：第 i 个样本的预测值

• L_MSE​：损失值（越小越好）

6.4 批量与迭代设置

• 批大小（Batch size）：64（兼顾显存与梯度稳定性）

• 训练轮数（Epoch）：150

• 提前停止（Early stopping）：验证集 10 轮无提升则停止

6.5学习率调度

采用 ReduceLROnPlateau：

• 验证集损失连续 5 轮无提升 → 学习率 × 0.5

• 最低学习率：1×10^{-6}

6.6正则化与防过拟合

• Dropout（0.5）

• 数据增强（窗口随机平移、加微弱高斯噪声）

• L2 正则化（λ=1e-4）

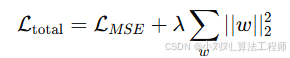
在损失函数中加上权重平方和，防止权重过大导致模型过拟合。

其中：

• L_total​：总损失

• L_MSE：均方误差

• λ：正则化系数（控制惩罚强度）

• w：模型参数（权重向量）

• ||w||_2^2：权重向量的平方和

7. 实验结果与分析

7.1 评估指标

采用以下指标对模型性能进行评估：

（1）平均绝对误差（MAE）：衡量预测值与真实值之间的平均绝对差异，公式如下：

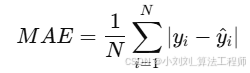
衡量预测值与真实值之间的平均绝对差异，反映整体预测的平均偏离程度。MAE 越小，预测结果整体越接近真实值。

其中：

• N：样本总数

• y_i：第 i 个样本的真实值

• hat{y}_i：第 i 个样本的预测值

• |y_i - hat{y}_i|：第 i 个样本的预测误差绝对值

（2）均方根误差（RMSE）：反映预测值与真实值之间的离散程度，公式如下：

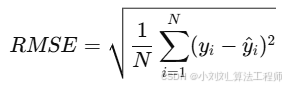
衡量预测值与真实值之间的离散程度，RMSE 对较大误差更敏感。RMSE 越小，说明预测结果越稳定且精度越高。

其中：

• N：样本总数

• y_i：真实值

• hat{y}_i：预测值

• (y_i - hat{y}_i)^2：第 iii 个样本的预测误差平方

（3）相关系数（R）：表示预测值与真实值之间的线性相关性，公式如下：

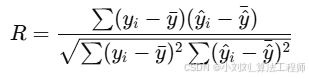
衡量预测值与真实值之间的线性相关性，取值范围 [−1,1]。R>0：正相关；R<0：负相关；R=1：完全正相关；R=0：无线性相关性。

其中：

• y_i​：真实值

• hat{y}_i​：预测值

• bar{y}：真实值的均值

• bar{\hat{y}} ：预测值的均值

• 分子：真实值与预测值的协方差

• 分母：真实值和预测值的标准差乘积

（4）标准差（STD）：评估预测误差的波动范围，公式如下：

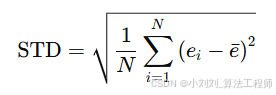
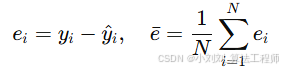
反映预测误差的波动范围，STD 越小表示预测误差越集中、模型稳定性越高。

其中：

• ei​：第 iii 个样本的预测误差

• bar{e}：预测误差的均值

• N：样本总数

• STD：预测误差的标准差

（5）均方误差（MSE）：综合考虑预测误差的平方和，公式如下：

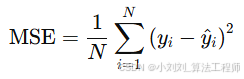
反映预测值与真实值之间的平均平方差，放大了较大误差的影响，因此对离群值更敏感。MSE 越小，预测精度越高。

其中：

• yi​：真实值

• y^i​：预测值

• N：样本总数

• (yi−y^i)2：预测误差的平方

7.2 三种输入模式结果对比

通过对 SBP、DBP 和 MAP 三种血压指标的预测结果进行多维度可视化分析，能够更直观地评估模型性能及误差特性。

（1）模型性能比较

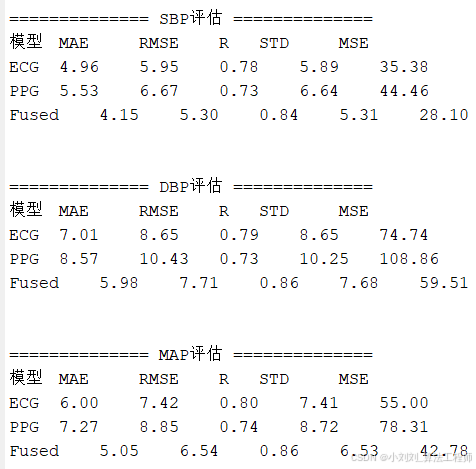
从预测结果可以看出，融合ECG和PPG信号特征的模型在SBP、DBP和MAP预测任务中均取得了最佳性能，其MAE、RMSE等误差指标最低，相关系数R最高。这表明融合模型能够综合利用ECG和PPG信号中的互补信息，提高血压预测的准确性。

（2） ECG与PPG模型对比

预测值与真实值的时间序列曲线对比显示，融合模型在时间维度上更好地捕捉血压变化趋势，拟合度明显优于单一信号模型（ECG 或 PPG）。

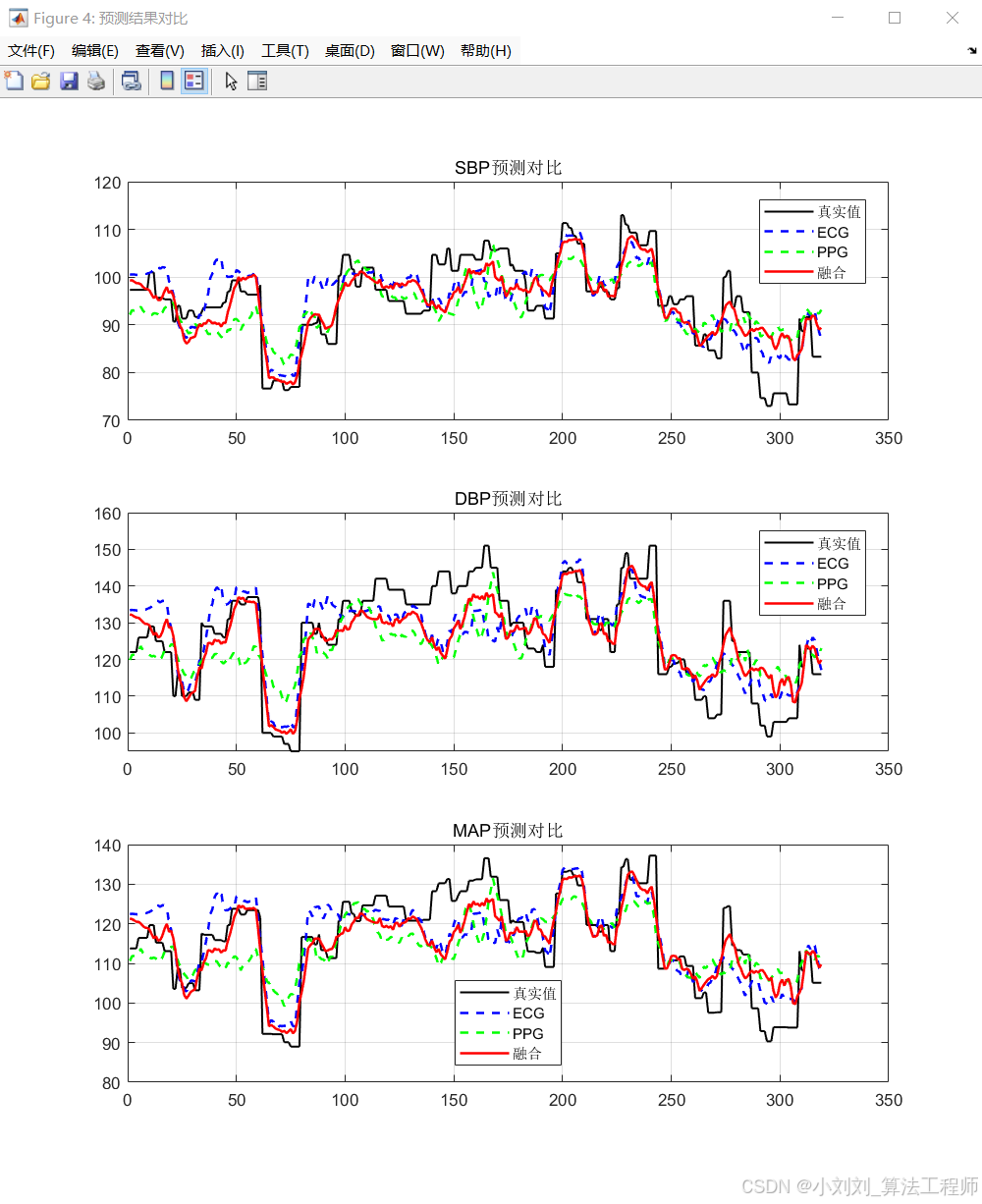
对比ECG模型和PPG模型的预测结果，发现PPG模型在SBP预测方面略优于ECG模型，而ECG模型在DBP预测方面表现相对较好。这可能是因为PPG信号与SBP的相关性更高，而ECG信号与DBP的关联性更强。

（3）散点图相关性分析与误差分布分析

通过绘制预测误差的箱线图，观察到融合模型的误差分布更集中，且中位数接近零，说明融合模型的预测结果更稳定，误差更小。

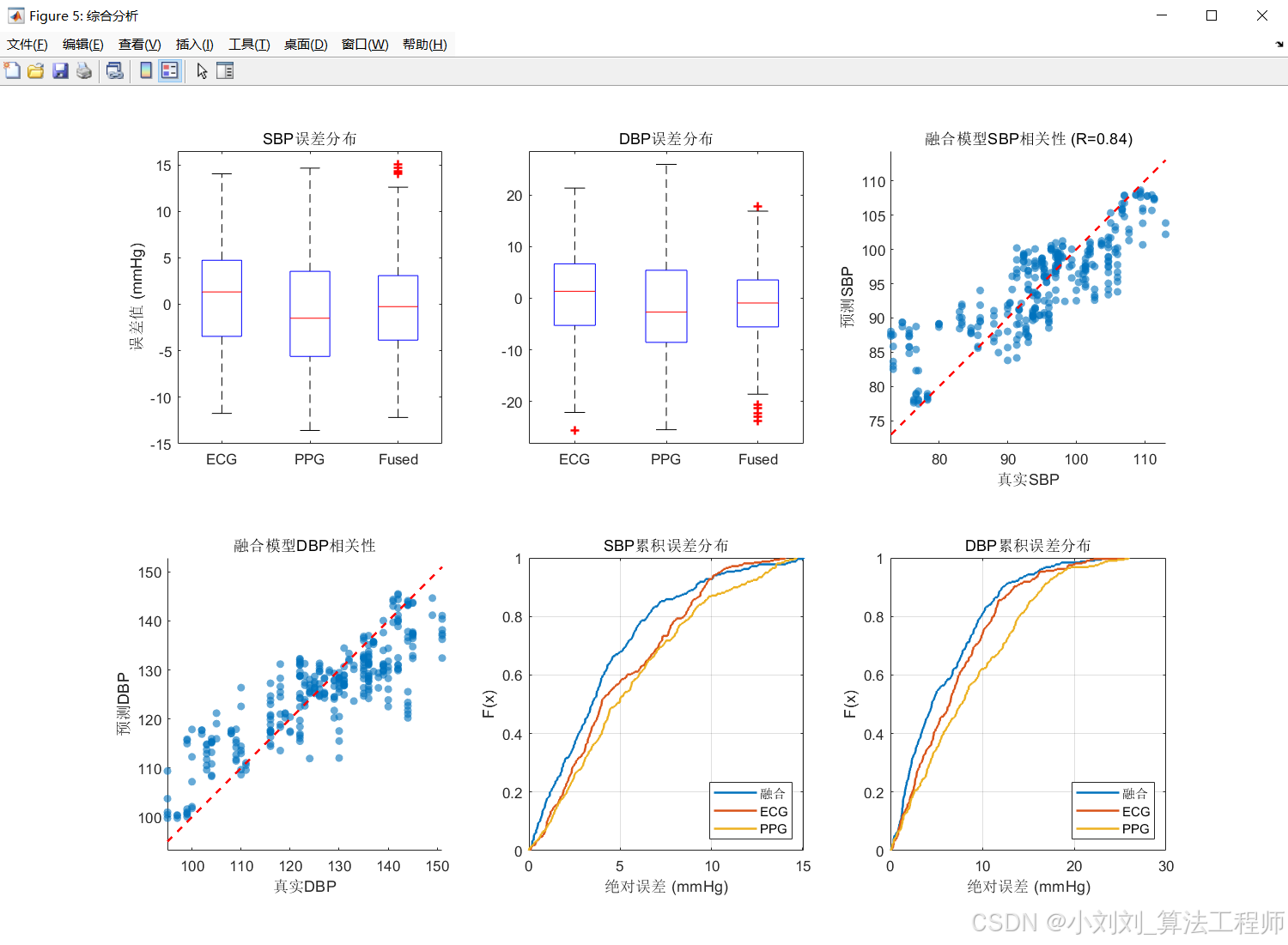
散点图相关性分析进一步验证了这一点，融合模型的相关系数（R 值）均达到 0.84 以上，显示出预测值与真实值之间更强的线性相关性，尤其是在 DBP 和 MAP 预测中表现突出。误差分布直方图揭示，融合模型的误差更集中，标准差（STD）和均方误差（MSE）均明显低于单一模型，说明其预测误差波动更小，结果更稳定。

（4）Bland-Altman分析

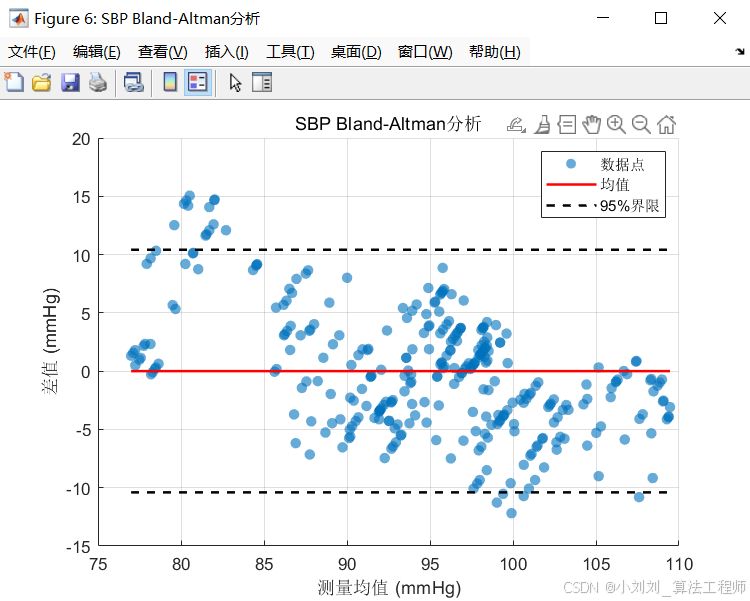
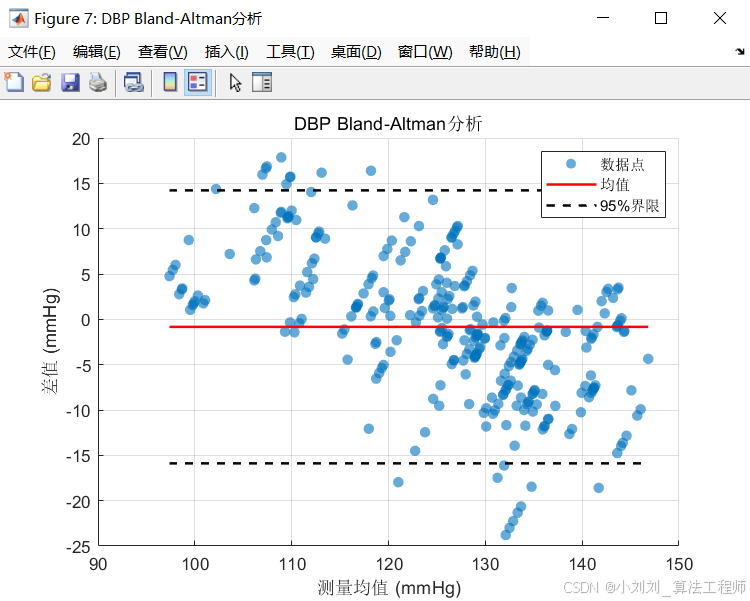
进行Bland-Altman分析，绘制预测值与真实值之间的差值与平均值的关系图。结果显示，融合模型的大部分差值落在95%置信区间内，进一步证明了融合模型的可靠性和一致性。

7.3 结果分析

• ECG 优于 PPG：在 SBP、DBP、MAP 三类指标预测中，ECG 模型在 MAE、RMSE、R 等方面均优于 PPG，说明 ECG 信号的血压相关特征更明显。

• 融合模型最优：ECG+PPG 融合模型在全部指标上均表现最佳，精度和稳定性显著提升，尤其是 DBP 预测改进幅度更大。

• 稳定性与相关性兼顾：融合模型 STD、MSE 最小，R 最大，说明其预测结果精度高、波动小且与真实值线性相关性强。

**综上，**融合模型在多项评估指标和多角度可视化分析中均表现优异，展示出更准确、稳定且临床意义明确的血压预测能力。

Tips：下一讲，我们将进一步探讨，心电信号处理与应用的其他部分。

以上就是基于ECG和PPG信号的血压预测的全部内容啦~

我们下期再见，拜拜(⭐v⭐) ~

（Ps：有代码实现需求，请见主页信息，谢谢支持！~）