无线通信与雷达感知融合的波形设计与信号处理(上)
C. Sturm and W. Wiesbeck, "Waveform Design and Signal Processing Aspects for Fusion of Wireless Communications and Radar Sensing," in Proceedings of the IEEE, vol. 99, no. 7, pp. 1236-1259, July 2011, doi: 10.1109/JPROC.2011.2131110.
引言
在当前的技术发展中,雷达和无线通信系统的射频前端架构变得越来越相似。特别是,越来越多的传统由硬件组件实现的功能正被数字信号处理所取代。与此同时,通信系统使用的载波频率已经转移到微波频段,其数量级与传统雷达应用所使用的频率相当。因此,利用现有技术可以轻松实现用于通信和雷达应用的联合射频硬件平台。这种平台将为新型系统概念和应用提供独特的可能性。更重要的是,通过使用联合波形同时服务于两种应用,所占用的频谱将被非常高效地利用,两种应用可以同时运行,这将保证两种功能的永久可用性,并有助于部分克服频谱资源有限的问题。这种在单一硬件平台上使用单一波形提供雷达和通信功能的系统,在本文中被称为"RadCom"系统。
智能交通应用是RadCom系统的一个重要应用领域,它需要与其他车辆建立通信链路,同时需要主动环境感知功能。借助合适的系统平台,道路上的所有车辆都可以在协作雷达传感器网络中进行交互,提供独特的安全功能和智能交通路由。此外,与仅提供纯粹车对车通信功能的系统相比,同时提供通信和雷达功能的联合系统的市场推广会容易得多。由于车对车通信系统只有在通信伙伴存在时才能提供信息,在市场推广初期,潜在客户没有太多动力让他们的汽车配备纯粹的车对车通信系统。然而,RadCom系统无论市场渗透率如何,都能始终为客户提供价值------这得益于其雷达感知功能。
此外,可以预期在联合系统中,两种应用都将从相互共享信息中受益。例如,雷达应用可以使用通信网络上分布的信息来提高其检测概率和精度。最终,甚至可以实现从不同平台获取的雷达图像的完全融合,这将允许将传感器范围扩展到远超传播限制的距离。
RadCom开发的主要挑战在于找到可以同时用于信息传输和雷达感知的合适波形。因此,本文的主要范围是识别和评估用于该目的的不同方法。应该强调的是,即使本文中提出的研究侧重于汽车应用,所讨论的概念和波形也可以用于任何需要同时进行雷达感知和通信的应用场景,例如航空和军事应用。
经典雷达波形设计旨在创建具有最佳自相关特性的波形,这在接收器中应用相关处理时保证了测量的高动态范围。满足此要求的最流行的例子是线性调频(LFM)脉冲,也称为"chirp"信号。因此,设计联合波形的最直观方法是使用线性频率调制来编码数据。然而,这种方法的缺点是通信符号率仅对应于chirp速率,这通常比专用通信系统在相同带宽内实现的符号率低几个数量级。因此,从通信的角度来看,这种方法不是最优的。为了在符号率方面实现更好的通信性能,必须应用源自数字通信的连续发射信号。具有良好自相关特性的典型通信波形是扩频信号,它是联合雷达和通信应用的著名候选者。此外,基于多载波通信波形的先进概念最近也出现了。使用多载波波形,可以应用频域处理技术,从而放宽自相关要求。本文的主要章节明确处理连续单载波和多载波波形,因为这些概念在为雷达和通信提供高性能方面最有前途。
波形设计的考量与要求
实现RadCom系统的第一步是识别适合无线通信和雷达应用的波形。波形的选择必须基于雷达的要求,特别是关于目标距离、多普勒和角度偏移的确定。对于这三者,动态范围和分辨率是目标检测和分离的关键要求。此外,在密集交通中,波形应对干扰和噪声具有鲁棒性。
对于通信而言,数据速率和误码率是最严格的参数。与雷达功能一样,波形应对干扰、噪声和多径传播引起的失真具有鲁棒性。为了在比特率方面提供高性能,必须选择具有足够高符号率的连续信号。由于传输的信息旨在到达邻近的所有RadCom系统,因此没有隐藏或保护信息内容的需求。
目前,对于汽车雷达应用,主要采用FM-CW(调频连续波)等波形,以及较少程度的脉冲FM。对于其他雷达应用,已知有许多其他波形(chirp、伪随机、交错、相位和频率编码等)。对于数字通信,特别是移动通信,两种概念主导着波形设计和应用:单载波波形和多载波波形(也常称为正交频分复用OFDM)。大多数最新的数字通信标准采用离散相位调制技术,如相移键控(BPSK、QPSK、8PSK)或更高阶的正交幅度调制方案(16QAM、64QAM)。在具有多径传播、多普勒和衰落的传播场景中,只有低阶调制方案(如BPSK和QPSK)能够成功实现。这一条件至少在具有多个接收器和单独传播信道的广播场景中成立,在这种场景中无法应用自适应调制。通过应用扩频技术(如直接序列扩频DSSS)可以获得额外的鲁棒性。OFDM波形包含频率分集,通过适当的编码,可以用于增加传输的鲁棒性。这些技术提供了许多优势,如接收器处理增益的可用性、信号频谱的白化以及功率谱密度的降低。
对于雷达应用,也存在类似于DSSS的原理,这些原理基于离散相位调制和二进制伪随机序列。一个典型的例子是m序列雷达,它采用伪随机m序列进行离散相位调制,以创建具有良好自相关特性的类噪声发射信号。多载波波形用于雷达目的的适用性也已得到证明。此外,在雷达应用中,DSSS或OFDM波形也可获得处理增益,这使系统具有鲁棒性,并允许在低接收信号功率或高干扰水平的场景中运行。因此,具有离散相位调制的波形为雷达和通信提供了联合基础,满足两种应用的要求。
单载波波形的数学表示
正交幅度调制的单载波波形(包括相位编码信号的特殊情况)通常由以下复基带信号表达式表示:
x(t)=∑i=0Nsym−1a(i)g(t−iT)x(t) = \sum_{i=0}^{N_{sym}-1} a(i)g(t - iT)x(t)=i=0∑Nsym−1a(i)g(t−iT)
其中NsymN_{sym}Nsym是组成信号帧的调制符号数,TTT表示符号持续时间,g(t)g(t)g(t)是基本基带脉冲形状,a(i)a(i)a(i)表示通过任何PSK或QAM调制方案获得的离散幅度和相位状态。
OFDM多载波信号的数学表示
OFDM多载波信号可以被视为具有正交载波波形的多个单载波信号的并行流,每个信号用不同的发送数据进行调制。其解析表达式为:
x(t)=∑μ=0Nsym−1∑n=0Nc−1a(μNc+n)exp(j2πfnt)rect(t−μTOFDMTOFDM)x(t) = \sum_{\mu=0}^{N_{sym}-1} \sum_{n=0}^{N_c-1} a(\mu N_c + n) \exp(j2\pi f_n t) \text{rect}\left(\frac{t - \mu T_{OFDM}}{T_{OFDM}}\right)x(t)=μ=0∑Nsym−1n=0∑Nc−1a(μNc+n)exp(j2πfnt)rect(TOFDMt−μTOFDM)
其中μ\muμ表示总共NsymN_{sym}Nsym个OFDM符号中的单个OFDM符号索引,nnn表示总共NcN_cNc个子载波中的单个子载波索引,aaa是复调制符号,fnf_nfn是单个子载波频率,TOFDM=T+TGT_{OFDM} = T + T_GTOFDM=T+TG是由基本符号持续时间TTT和保护间隔持续时间TGT_GTG组成的总OFDM符号持续时间,rect(t/TOFDM)\text{rect}(t/T_{OFDM})rect(t/TOFDM)描述了持续时间为TOFDMT_{OFDM}TOFDM的矩形窗。与单载波波形不同,对于OFDM传输,通常对各个子载波应用矩形脉冲形状。
为了使各个子载波正交且不相互干扰,必须满足以下条件:
fn=nΔf=nT,n=0,...,Nc−1f_n = n\Delta f = \frac{n}{T}, \quad n = 0, \ldots, N_c - 1fn=nΔf=Tn,n=0,...,Nc−1
即子载波之间的间隔Δf\Delta fΔf直接等于基本OFDM符号持续时间TTT的倒数。与相同数据速率的单载波传输相比,基本OFDM符号持续时间增加了NcN_cNc倍,这使得信号对快速衰落效应具有鲁棒性。保护间隔或循环前缀是对应于最大预期多径延迟的时域信号的部分循环重复,持续时间为TGT_GTG,允许完全补偿多径传播效应。循环前缀通常前置于OFDM符号的开头,占据总OFDM符号持续时间TOFDMT_{OFDM}TOFDM内的区间[0,TG)[0, T_G)[0,TG)。接收器仅评估区间[TG,TOFDM)[T_G, T_{OFDM})[TG,TOFDM),该区间不包含由多径传播引起的符号间干扰。
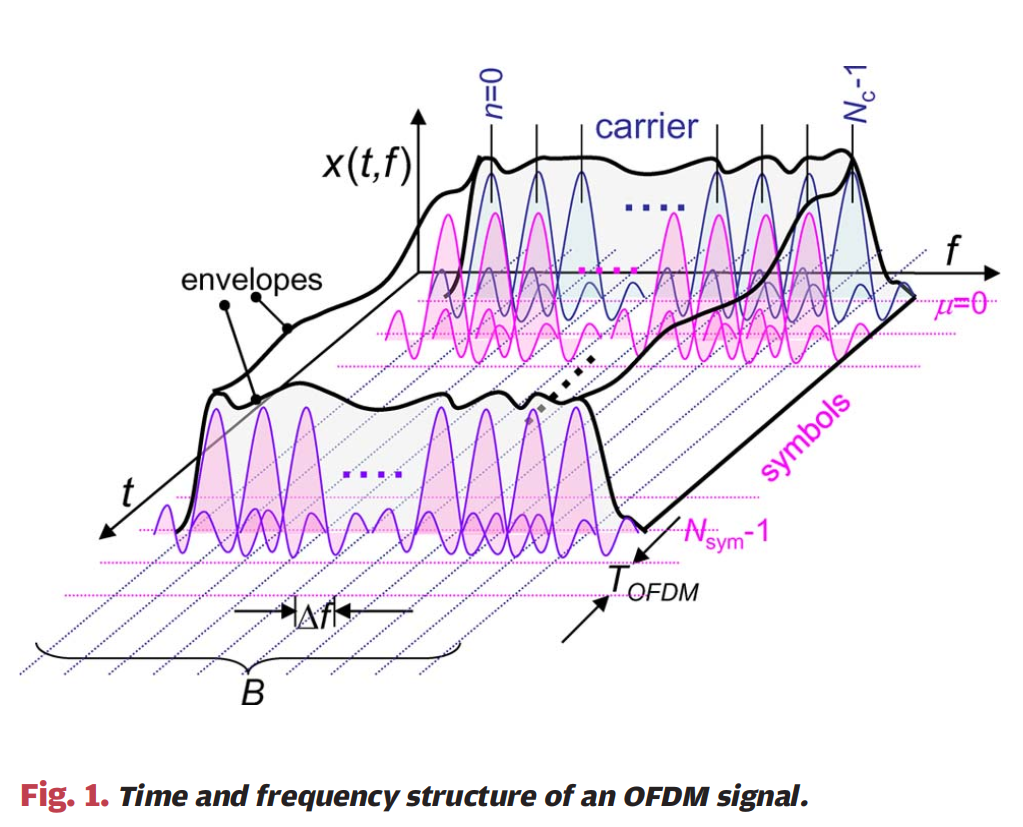
图1 :图1展示了OFDM信号的时间和频率结构。该图以三维方式呈现,横轴表示时间ttt,纵轴表示频率fff,第三个维度表示信号幅度x(t,f)x(t,f)x(t,f)。图中显示了NcN_cNc个子载波(从n=0n=0n=0到n=Nc−1n=N_c-1n=Nc−1)在频率轴上的分布,以及NsymN_{sym}Nsym个OFDM符号在时间轴上的排列。每个子载波的包络曲线清晰可见,子载波间隔为Δf\Delta fΔf,总信号带宽为BBB。每个OFDM符号的持续时间为TOFDMT_{OFDM}TOFDM。当子载波数量较多时,可以在时间和频率上实现准恒定的功率谱密度,输出信号呈现类噪声特性。
RadCom系统的工作原理
RadCom系统的一般操作原理是使用上述波形之一传输任意用户数据,必要时包括合适的信道编码策略。
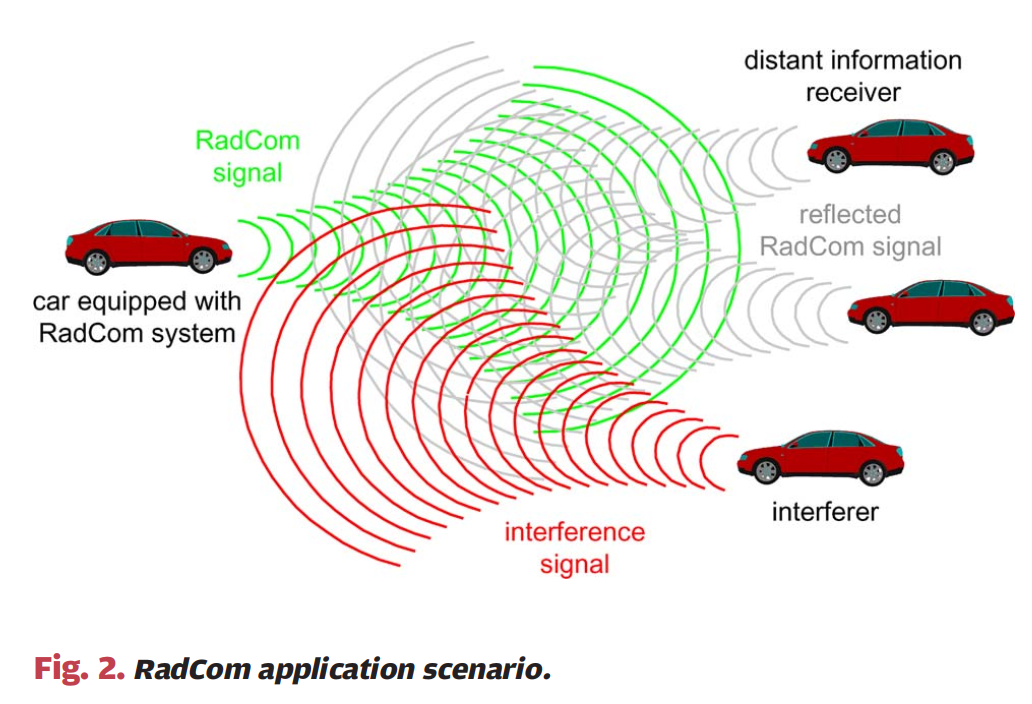
图2:图2展示了RadCom应用场景的示意图。左侧的汽车配备了RadCom系统,发射RadCom信号(图中以绿色表示)。该信号向远处的接收器传输信息。同时,该RadCom信号从邻近的物体(包括汽车)反射回来(反射信号以灰色表示)。RadCom系统观察其自身发射信号的回波,并通过应用合适的处理算法检测反射物体的存在及其距离和相对速度。此任务可以被解释为点目标检测。图中还显示了来自其他RadCom平台的干扰信号(以红色表示),说明必须假设有多个系统在同一频段内并行运行。反射发射信号的评估由数字信号处理执行,因此可以应用任意算法,无论是在时域还是频域操作。对于雷达处理,可以假设发射信号在雷达接收器处是完全已知的。由于打算使用连续发射信号,发射信号的持续时间将远长于信号的往返传播时间。这意味着接收器必须能够在发射期间监听,这需要发射天线和接收天线之间的适当解耦。
在以下章节中,特别讨论了如何为两种类型的波形实现合适的雷达处理算法,以及必须遵守的发射信号特性要求。此外,还详细研究了使用不同波形可以实现的雷达感知性能;主要标准是可以实现的动态范围。在此背景下,区分了雷达图像的动态范围(描述图像中主峰与平均噪声本底之间的比率)和峰值旁瓣比(PSL,描述主峰与最大旁瓣值之间的比率,无论是由傅里叶旁瓣还是不完美的自相关特性引起的)。
扩频单载波方法
信号编码原理
本节讨论基于单载波信号的RadCom实现。单载波信号不包含频率分集,因此使其适合雷达测量的自然方法是优化其自相关特性,并在接收器中执行时域相关处理。如第二节所述,在扩频通信以及m序列雷达的情况下,都应用了使用伪随机序列对发射信号进行编码的方法。使用纯m序列,其元素映射到2-PSK字母表a(i)∈{1,−1}a(i) \in \{1, -1\}a(i)∈{1,−1}来调制单载波波形,可以得到具有准最佳自相关特性的发射信号。
关于基于扩频信号实现联合雷达和通信应用的初步考虑多年前就已经报道。基本思想是应用具有足够高扩频因子的扩频编码,使得结果信号继承扩频码(即伪随机二进制码,如m序列)的良好自相关特性。在标准扩频传输中,数据序列的每个元素a(i)a(i)a(i)被替换为其与LLL个码序列元素相乘的结果。LLL称为扩频因子,结果符号序列c(i)c(i)c(i)的长度为LNsymLN_{sym}LNsym。扩频编码引入的冗余在保持编码器后符号率不变的情况下,按扩频因子的比例降低用户数据速率。另一方面,扩频编码可以通过码分多址(CDMA)用于用户分离。因此,这种方法为使用标准CDMA技术的多用户操作提供了固有支持。
相关处理的数学推导
如果发射信号从位于距离RRR处的物体散射回来,接收信号y(t)y(t)y(t)可以表示为:
y(t)=Ax(t−2Rc0)=A∑i=0LNsym−1c(i)g(t−2Rc0−iT)y(t) = Ax\left(t - \frac{2R}{c_0}\right) = A\sum_{i=0}^{LN_{sym}-1} c(i)g\left(t - \frac{2R}{c_0} - iT\right)y(t)=Ax(t−c02R)=Ai=0∑LNsym−1c(i)g(t−c02R−iT)
其中复幅度因子AAA描述了由于传播和散射过程而发生的衰减和相移,c0c_0c0是光速。
雷达处理器通过计算接收信号和发射信号之间的互相关函数ryx(t,τ)r_{yx}(t, \tau)ryx(t,τ)来估计到散射物体的距离:
ryx(t,τ)=∫t=0LNsymT(A∑i=0LNsym−1c(i)g(t−2Rc0−iT))×(∑k=0LNsym−1c(k)g(t−τ−kT)∗)dtr_{yx}(t, \tau) = \int_{t=0}^{LN_{sym}T} \left(A\sum_{i=0}^{LN_{sym}-1} c(i)g\left(t - \frac{2R}{c_0} - iT\right)\right) \times \left(\sum_{k=0}^{LN_{sym}-1} c(k)g(t - \tau - kT)^*\right) dtryx(t,τ)=∫t=0LNsymT Ai=0∑LNsym−1c(i)g(t−c02R−iT) × k=0∑LNsym−1c(k)g(t−τ−kT)∗ dt
这可以重写为:
ryx(t,τ)=A∑i=0LNsym−1∑k=0LNsym−1c(i)c(k)∫t=0LNsymTg(t−2Rc0−iT)×g(t−τ−kT)∗dtr_{yx}(t, \tau) = A\sum_{i=0}^{LN_{sym}-1} \sum_{k=0}^{LN_{sym}-1} c(i)c(k) \int_{t=0}^{LN_{sym}T} g\left(t - \frac{2R}{c_0} - iT\right) \times g(t - \tau - kT)^* dtryx(t,τ)=Ai=0∑LNsym−1k=0∑LNsym−1c(i)c(k)∫t=0LNsymTg(t−c02R−iT)×g(t−τ−kT)∗dt
显然,积分描述了基带脉冲形状g(t)g(t)g(t)的自相关函数rgg(τ)r_{gg}(\tau)rgg(τ)的时移版本:
ryx(τ)=A∑i=0LNsym−1∑k=0LNsym−1c(i)c(k)rgg(τ−2Rc0+(k−i)T)r_{yx}(\tau) = A\sum_{i=0}^{LN_{sym}-1} \sum_{k=0}^{LN_{sym}-1} c(i)c(k)r_{gg}\left(\tau - \frac{2R}{c_0} + (k-i)T\right)ryx(τ)=Ai=0∑LNsym−1k=0∑LNsym−1c(i)c(k)rgg(τ−c02R+(k−i)T)
因此,码序列的特性和基带脉冲自相关函数的形状都直接影响接收器中执行的相关结果。然而,由于kkk和iii的离散性质以及τ\tauτ的连续性质,上式的简化实际上是不可能的。如果假设g(t)g(t)g(t)是根升余弦滚降滤波器的脉冲响应,其最大峰值在t=0t=0t=0处,那么rgg(τ)r_{gg}(\tau)rgg(τ)将在τ=0\tau=0τ=0的条件下显示峰值。为了使时移自相关函数贡献其最大值,必须满足以下条件:
τ=2Rc0−(k−i)T\tau = \frac{2R}{c_0} - (k-i)Tτ=c02R−(k−i)T
然而,为了使ryx(τ)r_{yx}(\tau)ryx(τ)中出现峰值,序列c(i)c(i)c(i)和c(k)c(k)c(k)也必须以相干叠加的方式移位。当τ=0\tau = 0τ=0时:
k=i+⌊2Rc0T⌋k = i + \left\lfloor\frac{2R}{c_0T}\right\rfloork=i+⌊c0T2R⌋
因此,对于由物体距离确定的索引移位,在ryx(τ)r_{yx}(\tau)ryx(τ)中出现主峰。对于kkk和iii的其他组合,rgg(τ)r_{gg}(\tau)rgg(τ)贡献的值降低,其高度由g(t)g(t)g(t)的旁瓣电平决定。此外,发射符号序列c(i)c(i)c(i)的不完美互相关特性也会贡献额外的旁瓣。两种效应相互作用,导致复杂的旁瓣形状。为了获得最佳性能,应应用具有低旁瓣电平的脉冲形状g(t)g(t)g(t)。可以实现的最大峰值旁瓣比必须通过数值仿真来确定。上式的结果还表明,实现了与帧长度LNsymLN_{sym}LNsym相对应的处理增益。由于执行的相关是线性操作,可以分辨任意数量不同距离的散射体,它们将作为雷达图像中的不同峰值出现。
码序列与系统性能
对于所应用的伪随机序列的特性有不同的要求。对于通信应用,需要有一定数量的正交序列可供分配给不同用户。如果假设不同用户在时间上不同步,这一要求变得更加严格。在这种情况下,序列必须具有理想的互相关特性,即对于任何时间偏移,序列都必须正交。对于雷达处理的可操作性,所使用的发射序列必须具有理想的自相关特性,即其自相关函数必须产生单个峰值。如果要同时执行两种功能,伪随机序列必须满足两个要求,即具有理想的互相关和理想的自相关特性。已经分析证明,两个条件不能同时满足;在互相关函数的最大值和自相关函数的最大旁瓣上存在联合下界(Welch界):
max{∣rcc(i≠0)∣,∣rc1c2(i)∣}≥L2(M−1)LM−1\max\{|r_{cc}(i \neq 0)|, |r_{c_1c_2}(i)|\} \geq \sqrt{\frac{L^2(M-1)}{LM-1}}max{∣rcc(i=0)∣,∣rc1c2(i)∣}≥LM−1L2(M−1)
其中LLL表示伪随机序列的长度,MMM是可以从生成规则导出的不同码序列的数量。自相关函数的最大值随码长LLL线性增加,而根据上式,旁瓣大约随LLL的平方根增加。因此,通过足够高的码序列长度和选择适当的码族,可以实现非常低的旁瓣电平。具有少量成员MMM的著名码族是所谓的优选m序列(某一阶数所有可能m序列的子集)和Kasami序列。在以下研究中将考虑的其他流行伪随机码是Gold序列和混沌序列,后者由于其不可预测的行为而对安全应用特别有用。
系统仿真模型
为了验证所提出概念的可操作性,并研究关于可实现的雷达峰值旁瓣比的系统性能,在MatLab中实现了完整的系统模型。
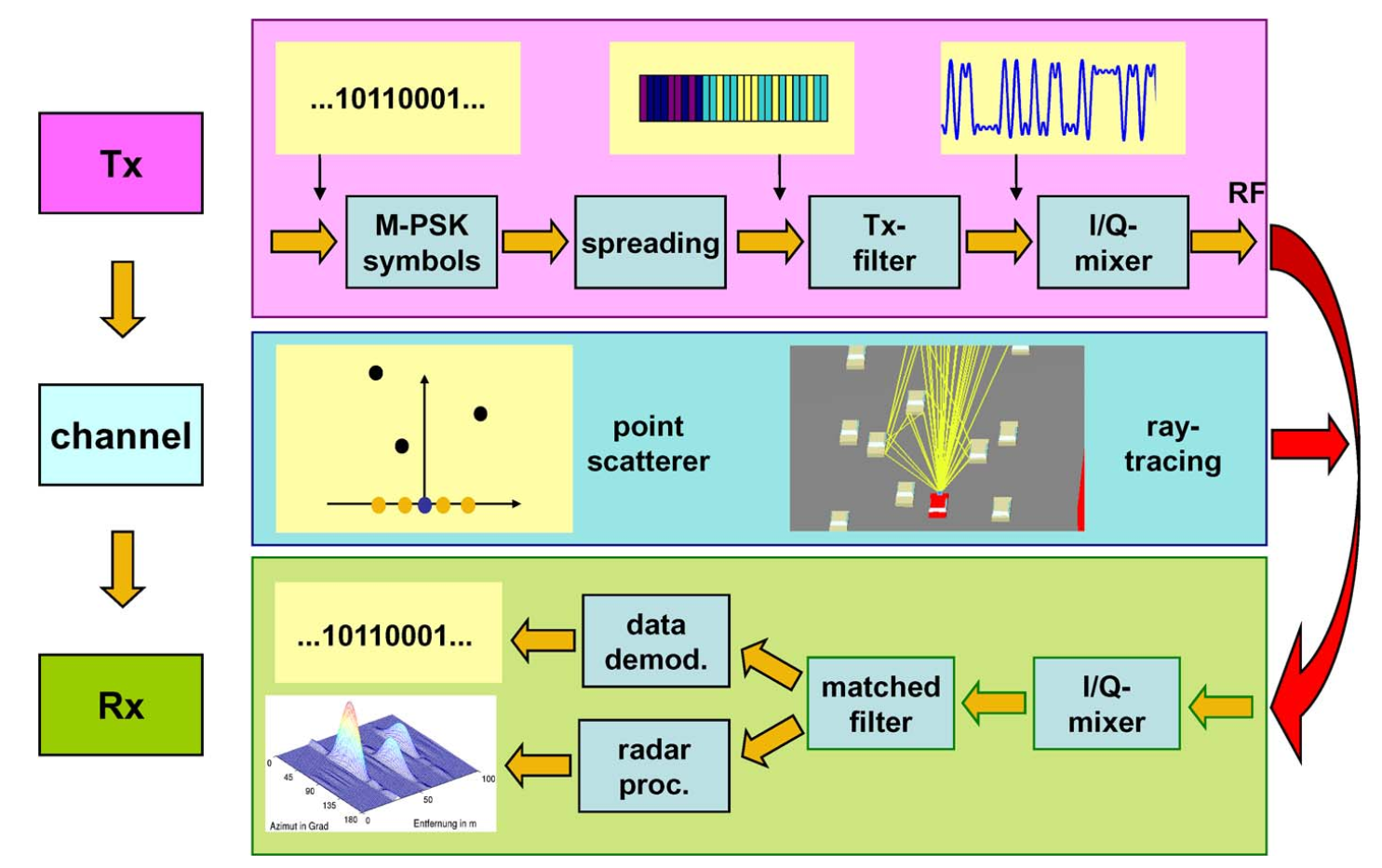
图3:图3展示了扩频雷达系统和场景仿真工具的框图。系统分为三个主要部分:发射器(Tx)、信道和接收器(Rx)。在发射器中,M-PSK符号首先经过扩频处理,生成编码符号序列"...10110001...",然后通过发射滤波器(Tx-filter)进行脉冲成形,再经过I/Q混频器上变频到射频(RF)进行发射。信道模型包括两种选择:点散射体模型和基于射线追踪的传播仿真器。点散射体模型对每个散射体单独计算时间延迟、衰减和相移,然后将散射信号叠加。接收器接收反射信号后,经过I/Q混频器下变频,通过匹配滤波器,然后分为两条路径:一条用于数据解调,另一条用于雷达处理。雷达处理器执行相关运算,输出雷达距离剖面(图中显示为距离-方位角的二维图像)。
在发射器中,扩频编码应用于随机生成的用户数据序列,然后每个编码的发射符号c(i)c(i)c(i)被映射到基本基带脉冲上,以创建连续的基带信号。结果基带信号在I/Q混频器中转换到载波频率。在传播仿真中,对任意数量的点散射体的信号传播和散射进行建模。对于每个散射体,单独计算时间延迟、衰减和相移。然后,将散射信号叠加。或者,可以采用基于射线追踪的真实道路场景传播仿真器。最后,在接收器中执行雷达处理。
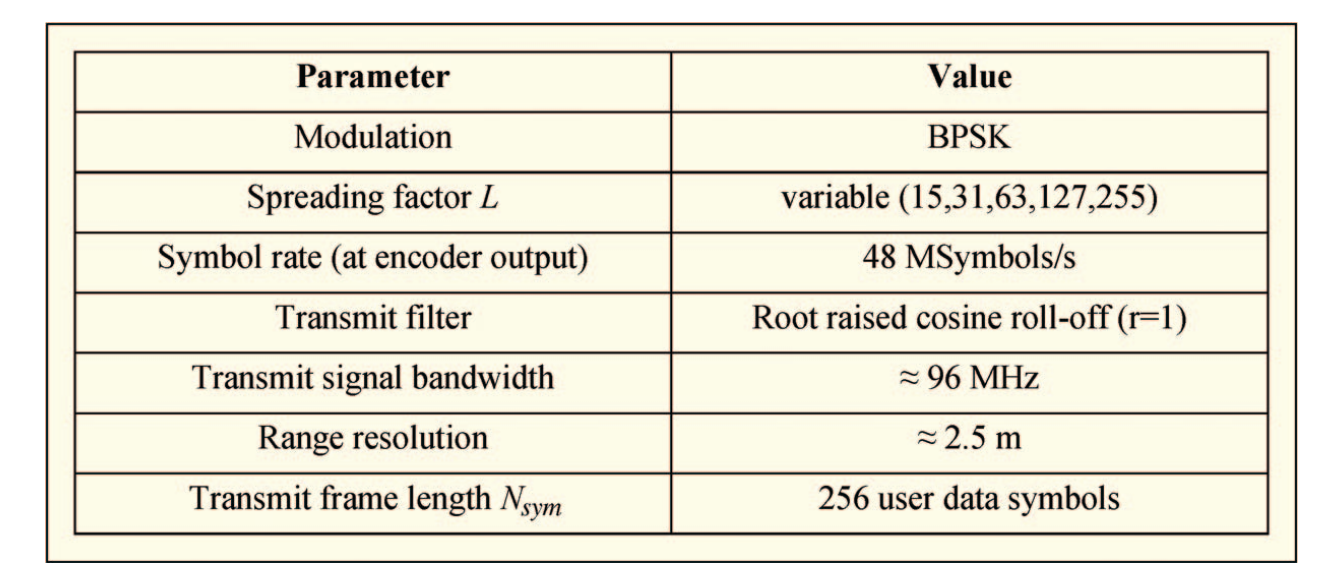
表1 :表1列出了扩频仿真模型的系统参数。调制方式为BPSK;扩频因子LLL可变,取值为15、31、63、127、255;编码器输出的符号率为48MSymbols/s;发射滤波器采用根升余弦滚降滤波器(滚降因子r=1);发射信号带宽约为96MHz;距离分辨率约为2.5m;发射帧长度NsymN_{sym}Nsym为256个用户数据符号。
编码符号c(i)c(i)c(i)的符号率在编码器输出处保持恒定值,以便具有与所应用扩频因子无关的恒定信号带宽。
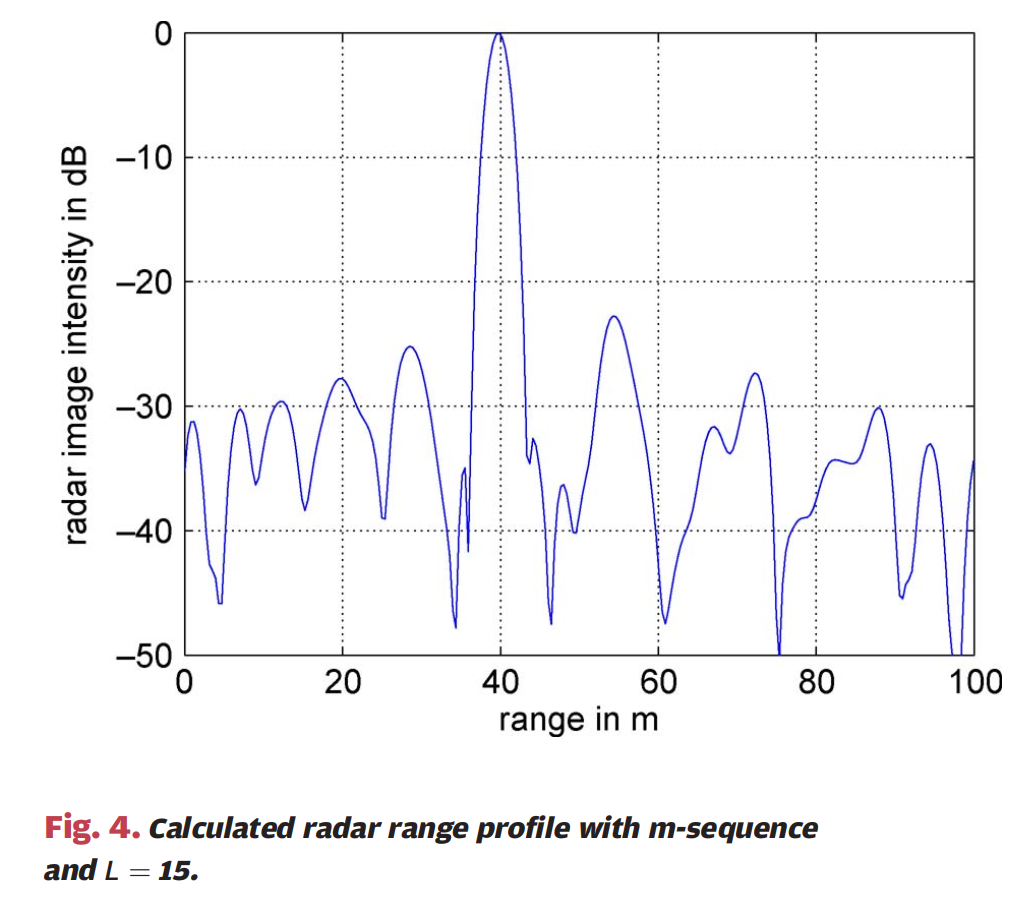
图4 :图4展示了使用m序列和扩频因子L=15L=15L=15计算的雷达距离剖面。横轴表示距离(单位:米),纵轴表示雷达图像强度(单位:dB)。图中显示了位于40m处的点散射体产生的主峰,峰值归一化为0dB。主峰的3dB宽度约为2.5m,大于理想可实现的1.5m,这种展宽是由根升余弦滚降滤波器引起的(可以被解释为频谱域中的cos2\cos^2cos2窗)。由于基带脉冲形状的旁瓣和发射序列非理想自相关特性产生的旁瓣之间的相互作用而产生的旁瓣清晰可见,它们看起来与典型的傅里叶变换旁瓣不同。尽管扩频因子相对较低(L=15L=15L=15),也实现了约-23dB的相对最大旁瓣电平。
雷达处理的积分时间对应于一个发射帧长度Nsym=256N_{sym}=256Nsym=256个用户数据符号,或NsymL=3840N_{sym}L=3840NsymL=3840个码符号,对应于36.6μs的帧持续时间。
除了扩频因子外,伪随机码序列的总长度和序列类型对旁瓣性能也有很强的影响。不同类型的伪随机序列已实现用于扩频编码。此外,区分和测试了两种扩频编码方法。在短码编码的情况下,伪随机序列随每个用户数据符号重复,即序列长度等于扩频因子。在长码编码的情况下,伪随机序列比扩频因子长得多,甚至不会在一个发射帧内重复。仿真中还包括来自第二个系统的干扰。使用相同的发射器模型计算来自第二个系统的干扰信号,但使用相同类型的不同伪随机序列进行编码。第一步假设固定的信干比为0dB。
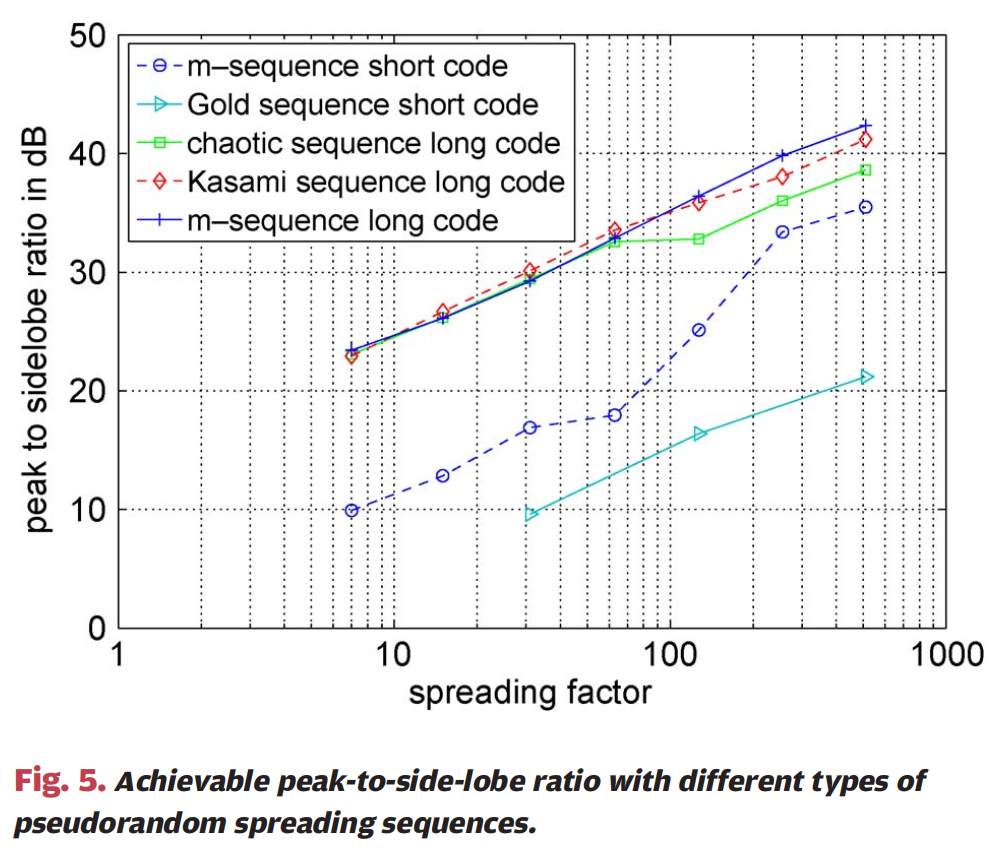
图5 :图5展示了使用不同类型伪随机扩频序列可实现的峰值旁瓣比。横轴为扩频因子(对数刻度,从1到1000),纵轴为峰值旁瓣比(单位:dB,从0到50dB)。图中比较了五种不同的编码方案:短码m序列、短码Gold序列、长码混沌序列、长码Kasami序列和长码m序列。结果显示,使用长码编码,与使用短码编码相比,可以实现显著更高的PSL。对于长码编码,m序列和Kasami序列(具有少量不同成员的码序列族的典型代表)表现相似且良好。对于扩频因子L=512L=512L=512,即使在存在干扰的情况下,也可以实现40dB或更高的动态范围。类似地,混沌序列也表现得相当好。使用短码编码,性能明显下降。特别是对于低扩频因子,与长码编码相比,PSL降低超过10dB。最差的结果是使用Gold序列获得的,Gold序列针对正交性进行了优化,已知具有相当差的自相关特性。
为了更深入地研究存在干扰时的性能,进行了不同干扰水平的仿真。在这些仿真中,仅考虑使用m序列的短码编码。
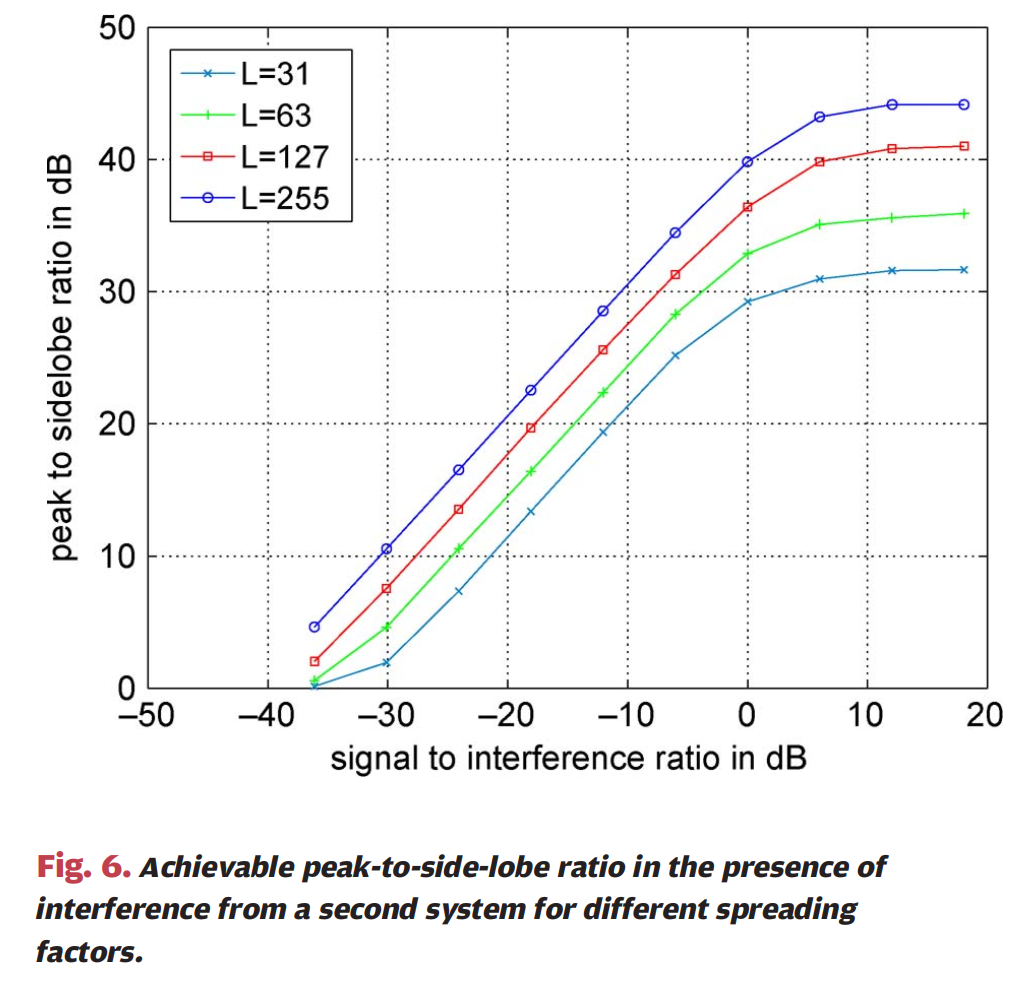
图6 :图6展示了存在来自第二系统干扰时不同扩频因子可实现的峰值旁瓣比。横轴为信干比(SIR,单位:dB,从-50到20),纵轴为峰值旁瓣比(单位:dB,从0到50)。图中显示了四种不同扩频因子(L=31L=31L=31、L=63L=63L=63、L=127L=127L=127、L=255L=255L=255)的性能曲线。对于低于0dB的信干比,可用动态范围几乎随干扰功率的增加而线性下降。从大约10dB的信干比开始,动态范围出现饱和,对于更好的信干比,性能没有明显改善。这是因为在这个区域,性能仅受码序列特性的限制,而不受干扰信号的影响。
应该提到的是,类似的研究也使用加性白噪声信号代替干扰进行了。与干扰情况下获得的结果相比,动态范围结果相同。这种一致性显然是扩频信号类噪声特性的结果。最后,可以得出结论,所研究的波形设计概念为雷达应用提供了30到40dB数量级的峰值旁瓣比,在存在非常强干扰时会下降。通过灵活选择扩频因子,系统配置可以适应不同的环境约束。
多普勒频移的影响
对于车辆环境中的应用,必须预期接收信号由于通信伙伴之间或雷达平台与反射物体之间的相对速度而产生频率偏移。在两个以相对速度vrelv_{rel}vrel运动的平台之间的通信链路情况下,接收器处的多普勒频移fDf_DfD为:
fD,comm=vrelλ=vrelfcc0f_{D,comm} = \frac{v_{rel}}{\lambda} = \frac{v_{rel}f_c}{c_0}fD,comm=λvrel=c0vrelfc
其中λ\lambdaλ是波长,fcf_cfc是载波频率。在雷达应用的情况下,由于双向传播,会发生两倍的多普勒频移:
fD,radar=2vrelλ=2vrelfcc0f_{D,radar} = \frac{2v_{rel}}{\lambda} = \frac{2v_{rel}f_c}{c_0}fD,radar=λ2vrel=c02vrelfc
因此,多普勒频移对雷达应用更为关键;所应用的波形必须能够承受上式描述的多普勒频移。理想情况下,不仅要设计雷达应用对多普勒频移具有鲁棒性,还要允许明确估计结果多普勒频移,以便能够确定反射物体的速度差。然而,使用扩频信号,这种估计几乎是不可能的。唯一的解决方案是计算与原始发射信号频率偏移副本的相关,这将需要极高的计算量,在实际实时应用中几乎不可行。
为了使系统对多普勒频移具有鲁棒性,计算相关的帧持续时间NsymLTN_{sym}LTNsymLT必须足够短,以使调制符号的相位在此期间不会受到多普勒频移的太大影响。为了研究所研究概念的实际鲁棒性,在信干比为0dB的情况下进行了不同多普勒频移的额外仿真。
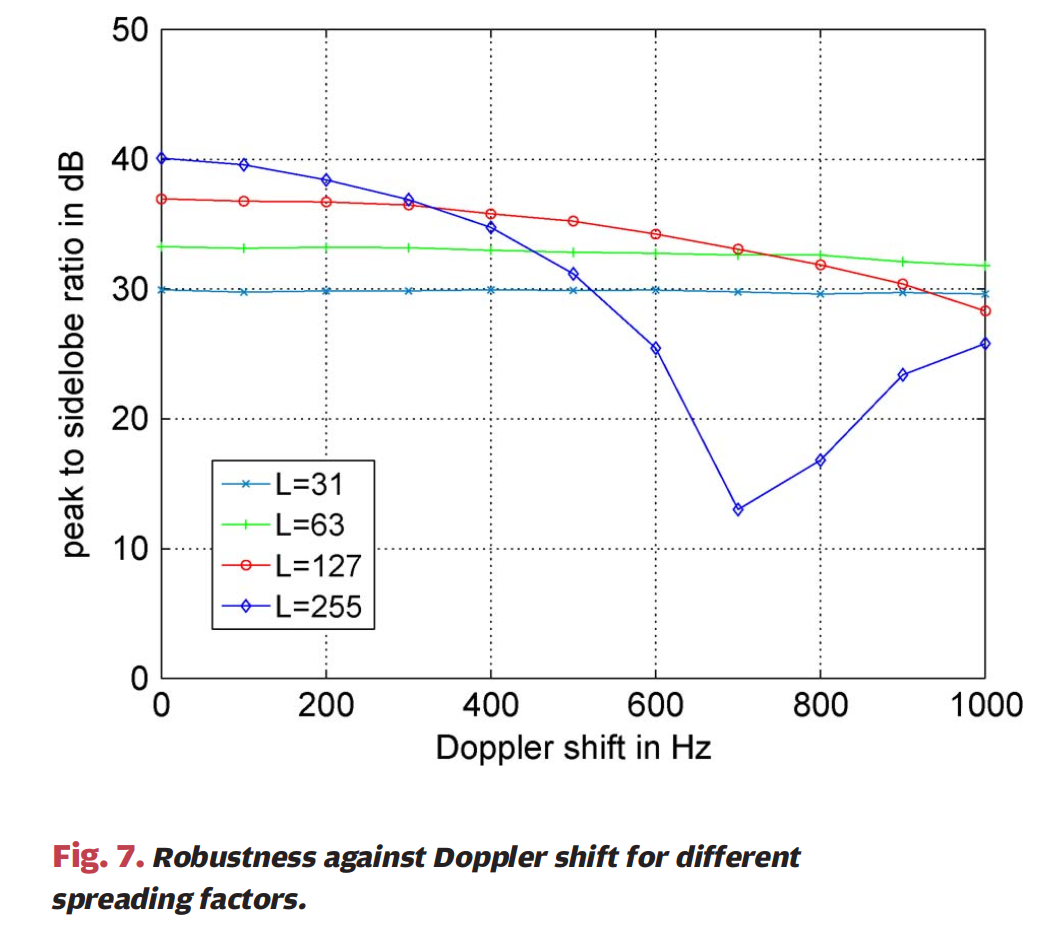
图7 :图7展示了不同扩频因子对多普勒频移的鲁棒性。横轴为多普勒频移(单位:Hz,从0到1000),纵轴为峰值旁瓣比(单位:dB,从0到50)。图中显示了四种不同扩频因子(L=31L=31L=31、L=63L=63L=63、L=127L=127L=127、L=255L=255L=255)的性能曲线。可以看出,较高的扩频因子最初提供更高的动态范围,但性能在多普勒影响下退化更快,在几百赫兹时就已经开始。令人惊讶的是,PSL并不是持续下降,而是在某个多普勒频移处开始再次上升,如L=255L=255L=255的情况所示。这种行为可以解释为,在旋转相位上积分会产生零阶贝塞尔函数。例如,对于载波频率24GHz,fD=1f_D=1fD=1kHz的多普勒频移对应于vrel=6.25v_{rel}=6.25vrel=6.25m/s(或22.5km/h)的相对速度。从图7可以看出,在具有运动物体的场景中,使用扩频信号进行雷达测量可以实现的PSL通常是有限的。
单载波波形的结论
可以得出结论,单载波通信信号与扩频技术相结合,通常适用于联合通信和雷达应用。对于通信应用,多用户操作是固有可能的,因为不同用户可以通过用户特定的码分离。同时,用户数据速率按扩频因子降低。然而,由于结果发射序列的准完美自相关特性,雷达测量中的动态范围仍然有限。使用长码编码以及m序列或Kasami码可以获得最佳性能。在具有运动物体的应用中,由于多普勒效应,积分时间受到限制。对于100MHz数量级的系统带宽,即使在存在干扰和适度多普勒频移的情况下,也可以实现40dB数量级的动态范围。汽车应用的一个主要缺点是,反射物体速度的估计将需要巨大的计算量。
OFDM多载波方法
OFDM信号雷达感知的经典方法
由于OFDM信号对衰落和多径传播效应的鲁棒性,它们已成为最近无线通信标准中的流行选择。典型的例子是WLAN标准IEEE 802.11.a/g/n、它们对车对车网络的适配IEEE 802.11.p,以及当前用于高数据速率移动通信的长期演进(LTE)标准的标准化过程。在雷达界,由于多载波信号能够灵活占用可用频谱资源和抵抗可能的干扰器,它们最近也在频率捷变波形的背景下引起了兴趣。与单载波波形(沿时间轴的单一维度描述)不同,多载波信号还包含沿频率维度的分集,因此可以被解释为占据时间和频率的二维空间。这一事实为应用复杂的雷达处理算法提供了多种机会,这些算法远远超出了经典的时域相关方法。
关于多载波波形用于雷达应用适用性的首批研究于2000年由Levanon发表。然而,在他的工作中,没有考虑通过编码和键控各个载波相位来传输信息。通过各子载波的相位调制将信息引入多载波信号,并实现频谱的高效双重使用的想法,直到很久以后的2006年才出现。在那个背景下,现在也明确使用了术语OFDM而不是多载波,假设OFDM信号如前所述,包括每个OFDM符号的循环前缀。然而,到目前为止,明确利用OFDM信号频率维度的可能性仍未完全实现。
在随后的几年中,提出了联合雷达和通信应用的详细系统概念。Garmatyuk等人开发了一个用于符合FCC超宽带(UWB)法规应用的联合雷达和通信OFDM系统。该系统以500MHz带宽运行,仅覆盖高达5m的短距离。接收器处的处理通过计算发射和接收基带信号的相关函数来进行。提供的结果显示相对较低的峰值旁瓣比,约为15dB。Tigrek等人发表了第一个包括OFDM雷达信号多普勒处理的概念。该应用是X波段监视雷达网络,信号带宽约为1MHz,工作距离约为50km;在这个概念中,接收器中的处理也是基于计算相关函数。为了确定多普勒,使用对应于不同多普勒频移的不同相关模板。除了计算多个相关函数的非常高的计算量外,这种方法的缺点是对于某个限制以上的目标距离,在子载波间隔的倍数处产生多普勒模糊,这取决于OFDM系统参数的选择。作者将循环前缀和后续OFDM符号之间的干扰确定为这些模糊的原因。为了实现无模糊的雷达图像(即使对于大目标距离),建议使用没有循环前缀和子载波上固定相位星座的特殊信号,然而这将同时禁用通信功能。
因此,可以得出结论,使用经典的基于相关的处理方法,在峰值旁瓣比和模糊性方面存在性能限制。此外,所有基于相关处理方法的概念都没有明确考虑信号的信息内容来优化雷达处理。开发一个考虑OFDM信号多载波结构并补偿用户数据影响的专用匹配滤波器的想法,最早由Berger等人在被动雷达应用的背景下描述。在这项工作中,还提出了多普勒估计的解决方案,该方案评估接收信号相对于时间的相移。
调制符号域中的OFDM雷达处理
下面考虑作者开发的OFDM信号先进联合距离和多普勒估计算法,它允许更简单和直观的描述,因为它直接操作发射和接收的调制符号,而不是基带信号。因此,它被称为"调制符号"域中的处理。这种方法充分利用了OFDM信号的二维信号结构,同时可以高效实现。这种方法的一般思想已在距离处理中引入。在这种方法中,用户数据在处理过程中被完全消除,这允许非常高的峰值旁瓣比,因为基带信号的不完美自相关特性不会影响估计。非常相似的概念可以在调制符号域中并行应用于多普勒估计。
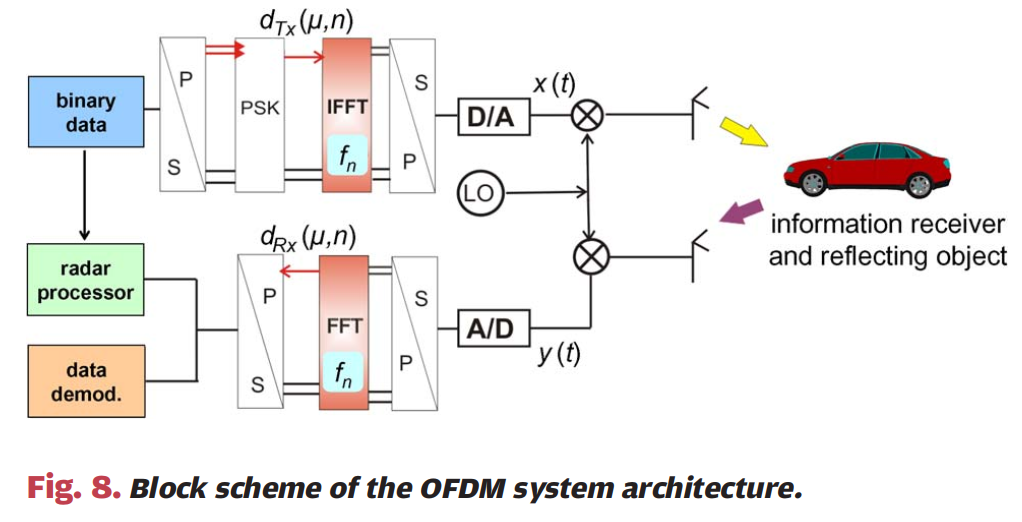
图8 :图8展示了OFDM系统架构的框图。在发射端,二进制用户数据首先经过串并转换(S/P),然后通过PSK调制映射为复值PSK符号,得到调制符号序列dTx(μ,n)d_{Tx}(\mu, n)dTx(μ,n)。通过块状逆快速傅里叶变换(IFFT)和随后的并串转换(P/S),计算出由正交载波波形fnf_nfn组成的时域信号x(t)x(t)x(t)。该信号经过数模转换器(D/A)转换为模拟信号,并与本地振荡器(LO)信号混频后在载波频率上辐射。在接收端,执行相同的步骤但顺序相反:射频信号经过下变频、模数转换(A/D),然后通过快速傅里叶变换(FFT)从接收的基带信号y(t)y(t)y(t)中恢复接收调制符号dRx(μ,n)d_{Rx}(\mu, n)dRx(μ,n)。信号被发送到反射物体,同时也被远处的信息接收器接收。接收调制符号被送入雷达处理器进行处理,同时也用于数据解调。
下面的考虑将揭示一种算法,该算法仅通过调制符号dTx(μ,n)d_{Tx}(\mu, n)dTx(μ,n)和dRx(μ,n)d_{Rx}(\mu, n)dRx(μ,n)的知识就可以执行雷达测量。如果按照前述公式描述的OFDM信号从距离RRR处的物体反射,并由于相对运动而产生多普勒频移fDf_DfD,则接收信号可以描述为:
y(t)=∑μ=0Nsym−1∑n=0Nc−1A(μ,n)dTx(μNc+n)×exp(j2πfn(t−2Rc0))exp(j2πfDt)×rect(t−μTOFDM−2Rc0TOFDM)y(t) = \sum_{\mu=0}^{N_{sym}-1} \sum_{n=0}^{N_c-1} A(\mu, n)d_{Tx}(\mu N_c + n) \times \exp\left(j2\pi f_n\left(t - \frac{2R}{c_0}\right)\right) \exp(j2\pi f_D t) \times \text{rect}\left(\frac{t - \mu T_{OFDM} - \frac{2R}{c_0}}{T_{OFDM}}\right)y(t)=μ=0∑Nsym−1n=0∑Nc−1A(μ,n)dTx(μNc+n)×exp(j2πfn(t−c02R))exp(j2πfDt)×rect(TOFDMt−μTOFDM−c02R)
其中dTx(μ,n)d_{Tx}(\mu, n)dTx(μ,n)是用户数据符号,与扩频传输不同,它们不受任何特定编码的约束。为了使距离和多普勒影响的差异更加清晰可见,上式可以重新排列为:
y(t)=∑μ=0Nsym−1exp(j2πfDt)∑n=0Nc−1A(μ,n)×{dTx(μNc+n)exp(−j2πfn2Rc0)}×exp(j2πfnt)rect(t−μTOFDM−2Rc0TOFDM)y(t) = \sum_{\mu=0}^{N_{sym}-1} \exp(j2\pi f_D t) \sum_{n=0}^{N_c-1} A(\mu, n) \times \left\{d_{Tx}(\mu N_c + n) \exp\left(-j2\pi f_n\frac{2R}{c_0}\right)\right\} \times \exp(j2\pi f_n t) \text{rect}\left(\frac{t - \mu T_{OFDM} - \frac{2R}{c_0}}{T_{OFDM}}\right)y(t)=μ=0∑Nsym−1exp(j2πfDt)n=0∑Nc−1A(μ,n)×{dTx(μNc+n)exp(−j2πfnc02R)}×exp(j2πfnt)rect(TOFDMt−μTOFDM−c02R)
接收器通过仅在基本OFDM符号持续时间T<TOFDMT < T_{OFDM}T<TOFDM内观察接收信号来恢复与一个OFDM符号相关的各个调制符号。只要保护间隔持续时间TGT_GTG被正确选择,接收器仍然从同一个OFDM符号中截取观察样本,因此可以忽略rect函数的时移。关于单个调制符号,可以看到,对于固定的OFDM符号索引μ\muμ,多普勒频率对同一OFDM符号内的不同调制符号没有单独的影响。相反,多普勒频率在每个子载波上引起相同的相移,前提是OFDM信号带宽远小于载波频率。另一方面,对于固定的子载波索引nnn,多普勒效应在该子载波上的连续调制符号之间引入线性相移,对应于多普勒频率在总发射OFDM符号持续时间内的相位变化2πfDTOFDM2\pi f_D T_{OFDM}2πfDTOFDM。此外,到反射物体的距离对一个子载波上后续调制符号之间的相移没有影响。然而,最重要的观察是,反射物体引入的距离和多普勒对调制符号具有完全正交的影响。距离仅沿频率轴引入线性相移,而多普勒也是如此,但仅沿时间轴。这种正交性成立的前提是观察持续时间足够短,使得反射物体保持在一个距离分辨率单元内。因此,必须能够使用合适的处理算法独立恢复距离和多普勒。
考虑到子载波间隔和相对速度与多普勒频率之间的关系,运动物体对接收调制符号dRx(n)d_{Rx}(n)dRx(n)的影响可以量化为:
dRx(μNc+n)=A(μ,n)dTx(μNc+n)exp(−j2πnΔf2Rc0)×exp(j2πμTOFDM2vrelfcc0)d_{Rx}(\mu N_c + n) = A(\mu, n)d_{Tx}(\mu N_c + n) \exp\left(-j2\pi n\Delta f\frac{2R}{c_0}\right) \times \exp\left(j2\pi\mu T_{OFDM}\frac{2v_{rel}f_c}{c_0}\right)dRx(μNc+n)=A(μ,n)dTx(μNc+n)exp(−j2πnΔfc02R)×exp(j2πμTOFDMc02vrelfc)
为了得到更具描述性的表示,调制符号帧现在被视为一个矩阵,其中每一列代表一个OFDM符号,每一行代表一个子载波:
D=(d(0)d(Nc)⋯d((Nsym−1)Nc)d(1)d(Nc+1)⋯d((Nsym−1)Nc+1)⋮⋮⋱⋮d(Nc−1)d(2Nc−1)⋯d(NsymNc−1))\mathbf{D} = \begin{pmatrix} d(0) & d(N_c) & \cdots & d((N_{sym}-1)N_c) \\ d(1) & d(N_c+1) & \cdots & d((N_{sym}-1)N_c+1) \\ \vdots & \vdots & \ddots & \vdots \\ d(N_c-1) & d(2N_c-1) & \cdots & d(N_{sym}N_c-1) \end{pmatrix}D= d(0)d(1)⋮d(Nc−1)d(Nc)d(Nc+1)⋮d(2Nc−1)⋯⋯⋱⋯d((Nsym−1)Nc)d((Nsym−1)Nc+1)⋮d(NsymNc−1)
这种重排可以应用于发射和接收的调制符号,因此上式中省略了下标。在相同的矩阵表示中,在运动物体反射后的接收调制符号为:
(DRx)μ,n=A(μ,n)(DTx)μ,n⋅(k⃗R⊗k⃗D)μ,n(\mathbf{D}{Rx}){\mu,n} = A(\mu, n)(\mathbf{D}{Tx}){\mu,n} \cdot (\vec{k}_R \otimes \vec{k}D){\mu,n}(DRx)μ,n=A(μ,n)(DTx)μ,n⋅(k R⊗k D)μ,n
其中(⋅)μ,n⋅(⋅)μ,n(\cdot){\mu,n} \cdot (\cdot){\mu,n}(⋅)μ,n⋅(⋅)μ,n表示矩阵的逐元素乘法,⊗\otimes⊗指并矢积,且:
k⃗R=(0exp(−j2πΔf2Rc0)⋯exp(−j2π(Nc−1)Δf2Rc0))\vec{k}_R = \left(0 \quad \exp\left(-j2\pi\Delta f\frac{2R}{c_0}\right) \quad \cdots \quad \exp\left(-j2\pi(N_c-1)\Delta f\frac{2R}{c_0}\right)\right)k R=(0exp(−j2πΔfc02R)⋯exp(−j2π(Nc−1)Δfc02R))
k⃗D=(0exp(j2πTOFDM2vrelfcc0)⋯exp(j2π(Nsym−1)TOFDM2vrelfcc0))\vec{k}D = \left(0 \quad \exp\left(j2\pi T{OFDM}\frac{2v_{rel}f_c}{c_0}\right) \quad \cdots \quad \exp\left(j2\pi(N_{sym}-1)T_{OFDM}\frac{2v_{rel}f_c}{c_0}\right)\right)k D=(0exp(j2πTOFDMc02vrelfc)⋯exp(j2π(Nsym−1)TOFDMc02vrelfc))
分别独立描述反射物体的距离和多普勒对接收调制符号的影响。从上述描述中,现在清楚地表明这些影响是正交的。
距离和速度估计算法的推导
为了实现距离和相对速度的处理器,第一步必须通过逐元素复除法从接收信息符号中去除发射信息:
(Ddiv)μ,n=(DRx)μ,n(DTx)μ,n=A(μ,n)(k⃗R⊗k⃗D)(\mathbf{D}{div}){\mu,n} = \frac{(\mathbf{D}{Rx}){\mu,n}}{(\mathbf{D}{Tx}){\mu,n}} = A(\mu, n)(\vec{k}_R \otimes \vec{k}_D)(Ddiv)μ,n=(DTx)μ,n(DRx)μ,n=A(μ,n)(k R⊗k D)
这产生了携带距离和多普勒信息的两个向量的并矢积。唯一剩余的任务是确定RRR和vrelv_{rel}vrel。为此,从向量描述返回到解析表示更为方便:
kR(n)=exp(−j2πnΔf2Rc0)k_R(n) = \exp\left(-j2\pi n\Delta f\frac{2R}{c_0}\right)kR(n)=exp(−j2πnΔfc02R)
kD(μ)=exp(j2πμTOFDM2vrelfcc0)k_D(\mu) = \exp\left(j2\pi\mu T_{OFDM}\frac{2v_{rel}f_c}{c_0}\right)kD(μ)=exp(j2πμTOFDMc02vrelfc)
在距离向量表达式中,距离RRR转换为沿频率轴的调制符号之间的线性相移。评估到反射物体距离的最方便方法是计算kR(n)k_R(n)kR(n)的离散傅里叶逆变换:
r(k)=IDFT[kR(n)]=1Nc∑n=0Nc−1kR(n)exp(j2πNcnk)=1Nc∑n=0Nc−1exp(−j2πnΔf2Rc0)exp(j2πNcnk)r(k) = \text{IDFT}[k_R(n)] = \frac{1}{N_c}\sum_{n=0}^{N_c-1} k_R(n) \exp\left(j\frac{2\pi}{N_c}nk\right) = \frac{1}{N_c}\sum_{n=0}^{N_c-1} \exp\left(-j2\pi n\Delta f\frac{2R}{c_0}\right) \exp\left(j\frac{2\pi}{N_c}nk\right)r(k)=IDFT[kR(n)]=Nc1n=0∑Nc−1kR(n)exp(jNc2πnk)=Nc1n=0∑Nc−1exp(−j2πnΔfc02R)exp(jNc2πnk)
k=0,...,Nc−1k = 0, \ldots, N_c - 1k=0,...,Nc−1
可以看出,当满足以下条件时,两个指数项相互抵消并产生单位值:
k=⌊2RΔfNcc0⌋,k=0,...,Nc−1k = \left\lfloor\frac{2R\Delta fN_c}{c_0}\right\rfloor, \quad k = 0, \ldots, N_c - 1k=⌊c02RΔfNc⌋,k=0,...,Nc−1
这意味着在时间响应r(k)r(k)r(k)的这个索引kkk处将出现一个峰值。类似地,可以通过对多普勒向量应用离散傅里叶变换来求解vrelv_{rel}vrel的确定:
v(l)=DFT[kD(μ)]=∑μ=0Nsym−1kD(μ)exp(−j2πNsymμl)=∑μ=0Nsym−1exp(j2πμTOFDM2vrelfcc0)×exp(−j2πNsymμl)v(l) = \text{DFT}[k_D(\mu)] = \sum_{\mu=0}^{N_{sym}-1} k_D(\mu) \exp\left(-j\frac{2\pi}{N_{sym}}\mu l\right) = \sum_{\mu=0}^{N_{sym}-1} \exp\left(j2\pi\mu T_{OFDM}\frac{2v_{rel}f_c}{c_0}\right) \times \exp\left(-j\frac{2\pi}{N_{sym}}\mu l\right)v(l)=DFT[kD(μ)]=μ=0∑Nsym−1kD(μ)exp(−jNsym2πμl)=μ=0∑Nsym−1exp(j2πμTOFDMc02vrelfc)×exp(−jNsym2πμl)
l=0,...,Nsym−1l = 0, \ldots, N_{sym} - 1l=0,...,Nsym−1
指数项的抵消和相干叠加产生的索引为:
l=⌊2vrelfcTOFDMNsymc0⌋,l=0,...,Nsym−1l = \left\lfloor\frac{2v_{rel}f_cT_{OFDM}N_{sym}}{c_0}\right\rfloor, \quad l = 0, \ldots, N_{sym} - 1l=⌊c02vrelfcTOFDMNsym⌋,l=0,...,Nsym−1
处理步骤完全独立于发射信息。这保证了高动态范围性能,因为只有典型的傅里叶旁瓣会产生。所有处理步骤都是线性运算,这保证了相同的方法适用于具有不同距离和相对速度的无限数量的反射物体。
实际实现算法的基础是接收调制符号矩阵DRx\mathbf{D}{Rx}DRx。完整的处理至少包括三个步骤。第一步,对所有矩阵元素执行逐元素复除法。下一个可选步骤是沿两个矩阵维度应用窗函数,以降低后续傅里叶变换引入的旁瓣电平。然后,第二个必要步骤是计算Ddiv\mathbf{D}{div}Ddiv每一行的离散傅里叶变换。最后,第三步是计算前一步骤得到的矩阵每一列的离散傅里叶逆变换。结果矩阵直接表示距离和多普勒的二维雷达图像。完整的算法非常适合实际应用,因为它只需要计算离散傅里叶变换,这是一个可以高效实现的标准过程。
由于傅里叶变换包含可以或多或少任意选择的归一化,雷达图像中的结果峰值不是处理增益的度量。相反,在每个傅里叶变换中,信号以相干确定性过程相加,产生N2N^2N2的总功率增益,而噪声作为随机量仅经历NNN的功率增益。这导致从距离处理得到的处理增益GPG_PGP等于NsymN_{sym}Nsym,从多普勒处理得到的处理增益等于NcN_cNc。因此,总处理增益GPG_PGP为:
GP=NcNsymG_P = N_cN_{sym}GP=NcNsym
这等于在最佳条件下使用相关处理器可以实现的处理增益,直接对应于相关样本的数量。调制符号域处理算法在分辨率和处理增益方面提供与相关处理器相同的性能。调制符号域处理方法的处理增益已通过测量验证。调制符号域处理算法也可以被解释为最大似然估计器。
系统参数化
为了找到适合实际车辆应用的OFDM系统参数集,进行了24GHz ISM频段的参数研究。大多数参数化标准实际上从通信和雷达角度来看是相同的,因为它们与信道的物理特性有关。信道的限制特性主要是多普勒扩展和最大多径延迟。一般来说,这些效应对雷达应用的影响更强,因为在这种情况下,由于双向传播,总是涉及因子2。假设典型交通场景中的最大相对速度为vrel,max=200v_{rel,max}=200vrel,max=200km/h(对应vrel,max=55.6v_{rel,max}=55.6vrel,max=55.6m/s),根据多普勒公式,反射信号的最大多普勒频移为fD,max=8.9f_{D,max}=8.9fD,max=8.9kHz。根据典型的OFDM系统设计规则,子载波间隔必须选择为Δf>10fD,max\Delta f > 10f_{D,max}Δf>10fD,max以确保子载波的正交性。
循环前缀的持续时间必须根据不同传播路径之间预期的最大延迟差来选择。对于雷达应用,必须假设发射天线和接收天线之间存在直接耦合,因此循环前缀持续时间必须根据系统平台与最远目标之间的往返传播时间来选择。由于雷达测量中的高衰减以及24GHz ISM规定的20dBm EIRP功率限制,合理假设最大可探测距离为200m,这导致最小循环前缀持续时间TG>1.33μsT_G > 1.33\mu sTG>1.33μs。对于通信应用,这一限制对应于传播路径之间400m的最大延迟差。
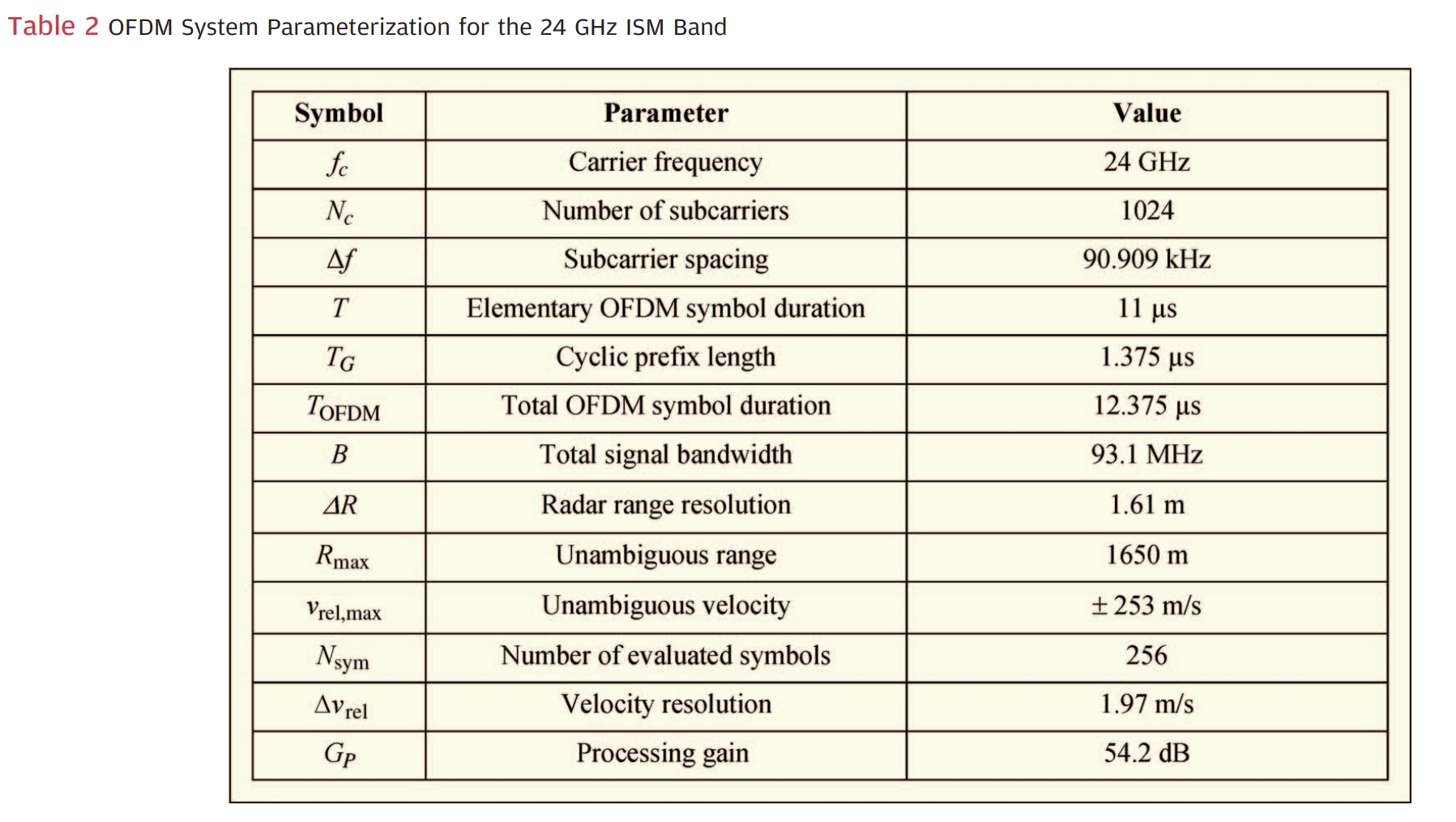
表2 :表2列出了24GHz ISM频段的OFDM系统参数化。载波频率fcf_cfc为24GHz;子载波数NcN_cNc为1024;子载波间隔Δf\Delta fΔf为90.909kHz;基本OFDM符号持续时间TTT为11μs;循环前缀长度TGT_GTG为1.375μs;总OFDM符号持续时间TOFDMT_{OFDM}TOFDM为12.375μs;总信号带宽BBB为93.1MHz;雷达距离分辨率ΔR\Delta RΔR为1.61m;无模糊距离RmaxR_{max}Rmax为1650m;无模糊速度vrel,maxv_{rel,max}vrel,max为±253m/s;评估符号数NsymN_{sym}Nsym为256;速度分辨率Δvrel\Delta v_{rel}Δvrel为1.97m/s;处理增益GPG_PGP为54.2dB。
除了信道的物理限制外,还有一些仅针对雷达操作的限制,主要涉及可能的模糊性。使用符号域处理,最大测量距离对应于信号在基本OFDM符号持续时间TTT内传播的距离。然而,基本符号持续时间通常比保护间隔TGT_GTG长得多,这意味着通过适当选择保护间隔,不需要考虑对TTT选择的额外要求。可以测量的多普勒频移fDf_DfD的最大绝对值受两个连续OFDM符号之间的时间步长限制,即TOFDMT_{OFDM}TOFDM。可以测量的最大绝对多普勒频移为1/(2TOFDM)1/(2T_{OFDM})1/(2TOFDM)。因此,为了覆盖广泛的可能相对速度vrelv_{rel}vrel,TOFDMT_{OFDM}TOFDM必须选择尽可能短,这意味着子载波间隔应尽可能大。显然,距离和多普勒测量的联合最优选择并不存在。相反,对于预期的汽车应用,必须找到适合的OFDM符号持续时间折衷,以满足典型道路场景的要求。作为结论,可以说明表2中的参数集满足通信和雷达角度的所有要求,因此保证了两种应用以高性能同时运行。
仿真结果
为了评估基于OFDM的方法,还应用了完整的仿真模型,包括OFDM发射器、点散射体传播模型和支持相关处理和调制符号域处理的OFDM接收器。为了量化调制符号域方法相对于标准相关处理器实现的改进,首先比较了单个反射物体的仅距离处理仿真结果。在仿真中,物体放置在距离R=30R=30R=30m处。
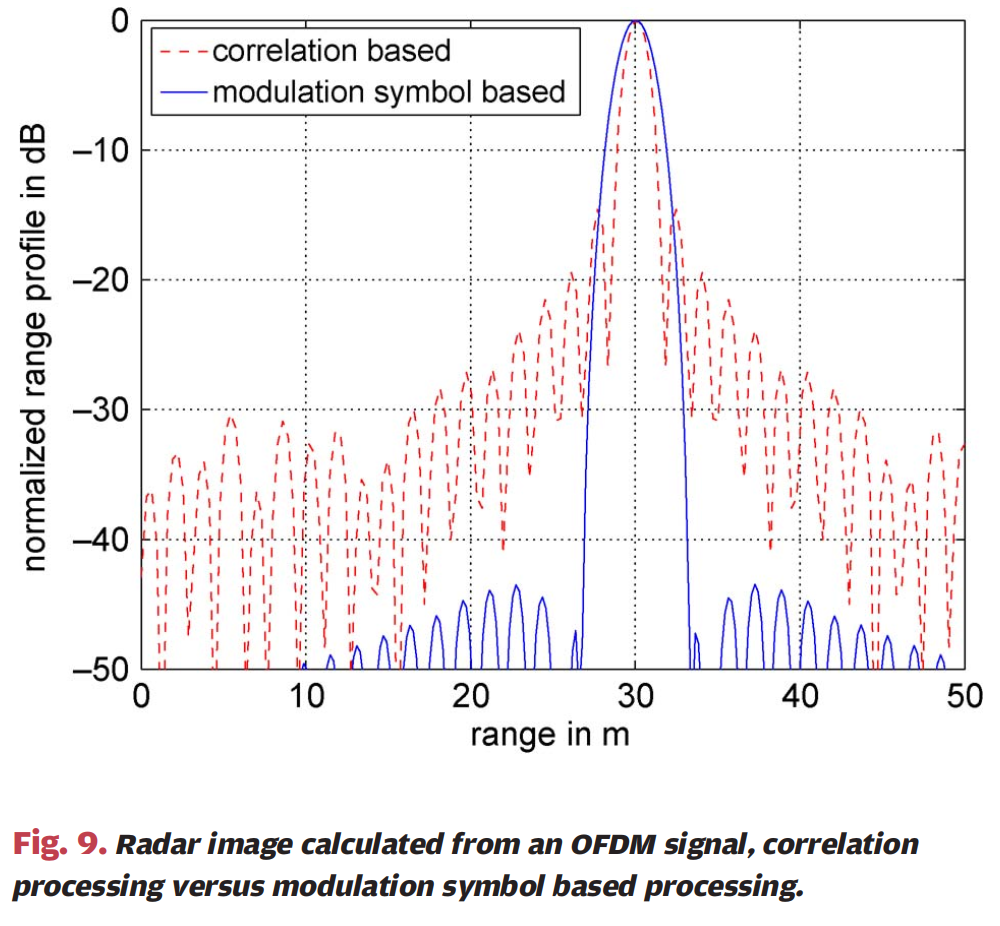
图9 :图9显示了从OFDM信号计算的雷达图像,比较了相关处理与调制符号域处理的结果。横轴为距离(单位:米,从0到50m),纵轴为归一化距离剖面强度(单位:dB,从0到-50dB)。图中有两条曲线:虚线表示相关处理的结果,实线表示调制符号域处理的结果。两种方法都在30m处显示主峰。调制符号域估计在Nsym=256N_{sym}=256Nsym=256个OFDM符号上执行,包括应用汉明窗。可以看出,调制符号域处理方法提供了显著更高的峰值旁瓣比。使用相关处理器,出现了两种不期望的旁瓣效应:首先,存在约-15dB电平的典型傅里叶一阶旁瓣(这是OFDM信号的固有特性,由OFDM发射器中的矩形脉冲成形产生);其次,存在约-30dB电平的额外旁瓣(例如在0到10m的距离范围内),这不是由傅里叶变换产生的,而是由发射数据中的内部相关产生的。必须假设,当传输真实用户数据而不是随机数据时,这些旁瓣的电平可能会更高。即使由矩形脉冲成形产生的傅里叶旁瓣可以通过专用滤波器抑制,也没有可能通过简单滤波器去除由内部数据相关引起的旁瓣,因为这些是发射信号的固有特性。另一方面,使用调制符号域处理方法,峰值旁瓣比仅受众所周知的傅里叶旁瓣限制。矩形脉冲形状的旁瓣和用户数据内相关的旁瓣都不会出现。由于汉明窗的应用,物体位置处的峰值被展宽。
然而,最重要的事实是表明所提出的调制符号域算法确实能够为多个反射物体独立估计距离和多普勒。为此,进行了具有3个点散射体的仿真,其中两个放置在距离R=30R=30R=30m处,第三个在R=35R=35R=35m处,同时只有第一个散射体被分配了vrel=5v_{rel}=5vrel=5m/s的相对速度,第二和第三个散射体以vrel=15v_{rel}=15vrel=15m/s运动。
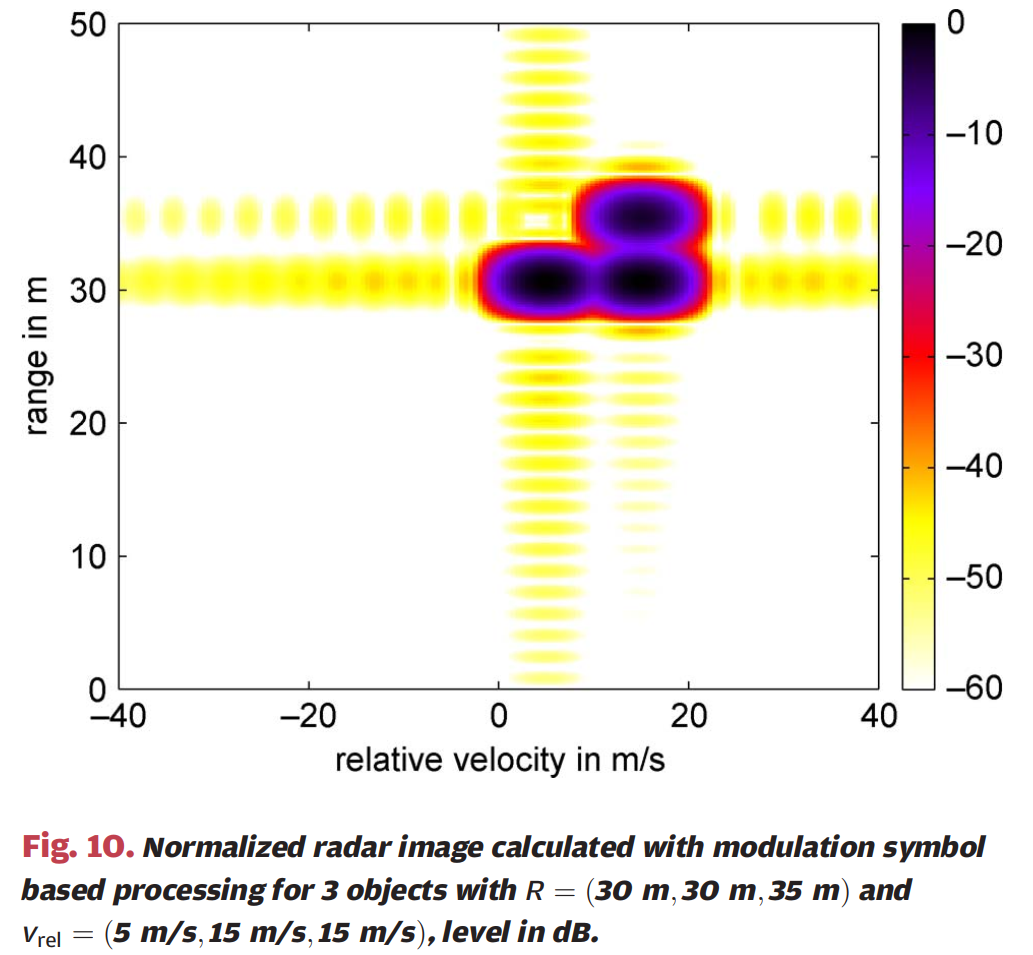
图10 :图10显示了使用调制符号域处理方法为Nsym=256N_{sym}=256Nsym=256计算的归一化雷达图像。横轴为相对速度(单位:m/s,从-40到40m/s),纵轴为距离(单位:米,从0到50m),颜色条表示归一化强度(单位:dB,从0到-60dB)。图中显示三个明亮的点,分别对应三个目标:距离30m、相对速度5m/s的目标;距离30m、相对速度-15m/s的目标;距离35m、相对速度-15m/s的目标。所有三个物体在雷达图像中作为单独的点出现在其对应的距离和相对速度位置。由于汉明窗的应用,旁瓣被很好地衰减到-40dB以下。仿真结果表明,即使多个物体位于相同距离或具有相同相对速度,也可以分离它们。距离和多普勒的估计是完全独立和正交的。
为了更好地了解潜在的系统性能,进行了不同噪声水平和不同评估OFDM符号数NsymN_{sym}Nsym的仿真。特别是,接收基带信号的SNRsignalSNR_{signal}SNRsignal在-40dB到40dB之间变化。在仿真中,评估了结果雷达图像信噪比SNRimageSNR_{image}SNRimage(物体引起的峰值与雷达图像中平均噪声电平之间的比率)以及峰值旁瓣比(PSL),针对不同NsymN_{sym}Nsym值,假设一个单点散射体。在这些仿真中,应用矩形窗以避免SNR损失,背景噪声电平的评估不考虑矩形窗产生的旁瓣。
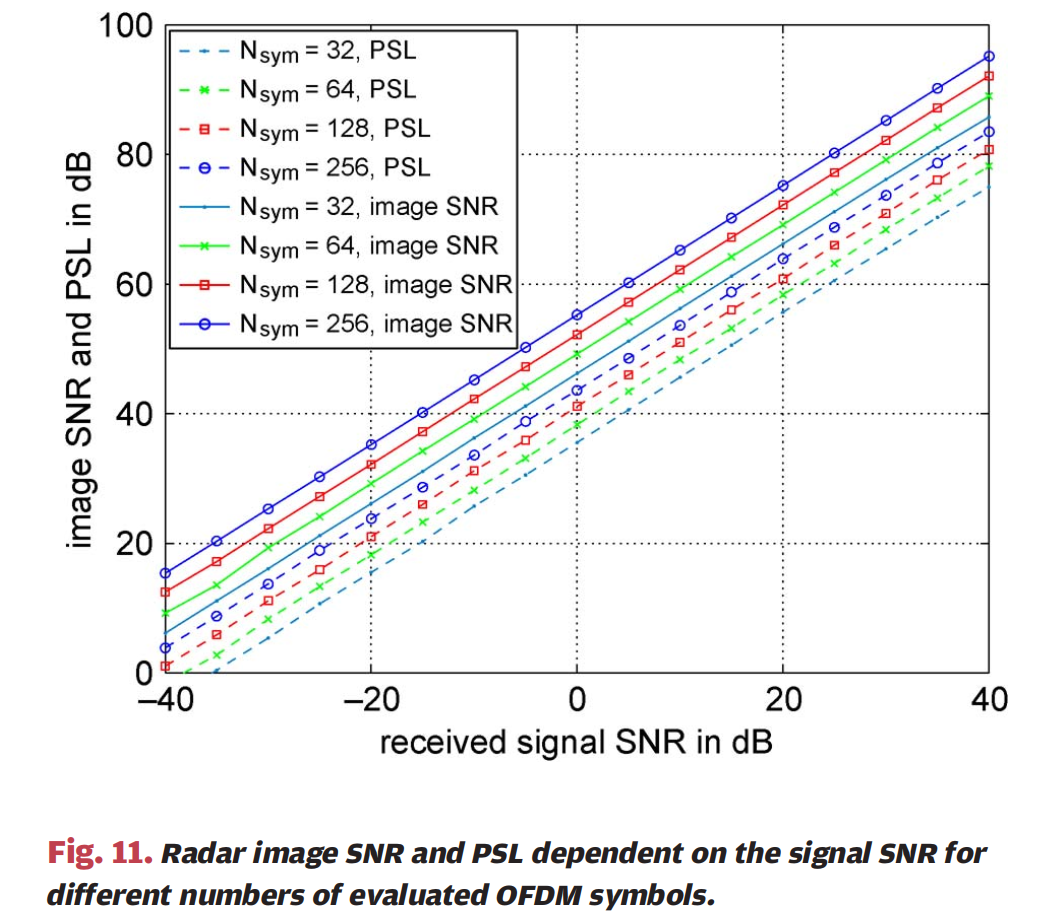
图11 :图11展示了雷达图像SNR和PSL随信号SNR的变化,针对不同数量的评估OFDM符号。横轴为接收信号SNR(单位:dB,从-40到40dB),纵轴为图像SNR和PSL(单位:dB,从0到100dB)。图中显示了八条曲线,分别对应Nsym=32N_{sym}=32Nsym=32、64、128、256的PSL(用符号标记)和图像SNR(实线)。可以看出,在双对数表示中,SNRimage和PSL都随SNRsignal线性改善。当比较相同NsymN_{sym}Nsym值时,SNRimage和PSL之间的差异保持恒定,约为12dB,这意味着在最坏情况下,背景噪声中的峰值超过平均背景噪声电平约12dB。通过将评估OFDM符号数NsymN_{sym}Nsym加倍,噪声电平降低3dB。处理增益非常高,保证即使对于低SNRsignal,雷达图像中的背景噪声相对于峰值保持在低水平。当Nsym=256N_{sym}=256Nsym=256且SNRsignal=0dB时,SNRimage为55.3dB,这对应于从处理增益公式理论上预期的处理增益。当比较OFDM系统概念的峰值旁瓣比结果与第三节中扩频方法获得的结果时,明显可以看出,使用OFDM方法结合调制符号域处理,可以实现高达80dB的更高峰值旁瓣比。使用扩频方法,动态范围往往在0dB的SNRsignal水平处饱和,动态范围约为40dB。这种效应在基于OFDM的方法中不会发生,可用峰值旁瓣比随着SNRsignal的增加而持续增长。这种行为源于这样的事实:在调制符号域处理方法中,发射的用户信息被完全去除,不会影响雷达处理的结果。此外,在调制符号域OFDM雷达处理方法中,多普勒被固有地补偿,这意味着多普勒频移不会像扩频方法那样限制积分时间。
应该提到的是,类似的研究已经进行,以研究来自其他OFDM信号的干扰对系统性能的影响。使用完全相同的仿真模型,除了用另一个具有相同参数但不同随机用户数据的OFDM信号代替白噪声,以不同的信干比添加到接收信号。结果表明,来自另一个OFDM信号的干扰与添加白噪声具有完全相同的影响,即只有背景噪声电平上升,但不会出现虚假目标。OFDM干扰影响下的SNRimage和PSL结果与图11所示的仿真结果相同。因此,基于OFDM的方法对干扰也非常鲁棒,处理增益公式也适用于对抗OFDM干扰。