图算法趣味学——图遍历

设计一条最优观光路线的问题，非常适合用图论来建模。根据我们的旅行偏好，可能希望恰好访问一组主要地标各一次、最小化总旅行距离，或者在目的地城市里走遍每一条商铺林立的街道。这些需求都可以归结为一个经典的图论问题：规划在图中的路径。

在本章中，我们将探讨这个核心问题的几种变体。哈密顿路径（Hamiltonian path） 要求恰好访问图中每个节点一次，可用于规划需要依次参观一组离散景点的行程。旅行商问题（Traveling Salesperson Problem，TSP） 的目标是访问每个景点并最小化总行程距离。欧拉路径（Eulerian path） 要求每条边仅走一次，适合规划不重复走街的"漫步"路线。

这些路径规划问题在现实中有着远超度假计划的应用，例如解决航运业中的物流调度问题。然而，它们在计算上往往颇具挑战性。虽然计算欧拉路径有高效算法，但哈密顿路径和旅行商问题都是 NP 困难（NP-hard） 的。本章将基于前面章节的技术，构建穷举算法来求解这些问题。

哈密顿路径与哈密顿回路

哈密顿路径（Hamiltonian path）以数学家威廉·哈密顿（William Hamilton）的名字命名，是一条在图中恰好访问每个节点一次的路径。我们可以把它看作是为一位"认真但容易厌倦的游客"制定的行程规划问题。游客需要在两个目标之间取得平衡：

1. 必须确保参观城市中的每一处景点，绝不遗漏。
2. 避免二次访问同一地点------毕竟，巨大的钟楼看过一次，就不必再看第二次了。

图 18-1 展示了一个在六个节点的图上的哈密顿路径 [0, 1, 2, 5, 4, 3]。路径从节点 0 出发，依次经过节点 1、2、5、4，最终到达节点 3。每个节点仅被访问一次。

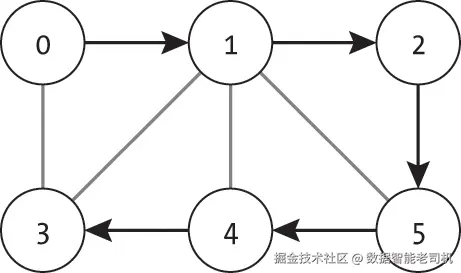
对于游客来说，更实用的是 哈密顿回路（Hamiltonian cycle 或 Hamiltonian circuit），它在恰好访问每个节点一次的同时，从同一个节点出发并回到该节点。虽然游客希望尽可能避免重复到访的景点，但他们也希望旅程能从酒店出发并在酒店结束------为了不用拖着行李在城里到处走，这是一个可以接受的折中方案。

在游客的例子中，我们用一个预先确定的节点（酒店）作为起点和终点，但哈密顿回路可以从图中的任意节点出发并结束。图 18-2 中的哈密顿回路示例可以从节点 0 出发，也可以从其他任意五个节点之一出发。

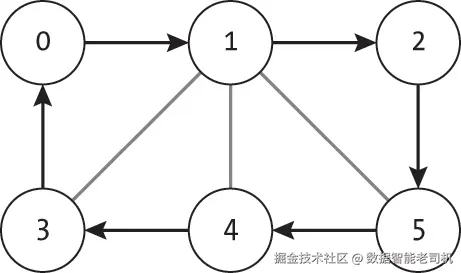
由于图 18-2 中的路径构成了一个环，因此路径上的所有节点都必须能够从自身到达自身。正如我们将看到的，这种灵活性在一般的哈密顿路径中并不适用。

验证哈密顿路径

要判断一条路径是否是哈密顿路径，我们需要检查该路径是否恰好访问了每个节点一次。我们定义了一个函数 is_hamiltonian_path() 来进行验证，该函数接收一个路径（由访问节点的列表表示）作为输入：

def is_hamiltonian_path(g: Graph, path: list) -> bool: 
    num_nodes: int = len(path)
  ❶ if num_nodes != g.num_nodes:
        return False

    visited: list = [False] * g.num_nodes
  ❷ prev_node: int = path[0]
    visited[prev_node] = True

    for step in range(1, num_nodes):
        next_node: int = path[step]

      ❸ if not g.is_edge(prev_node, next_node):
            return False
      ❹ if visited[next_node]:
            return False

        visited[next_node] = True
        prev_node = next_node

    return True

代码首先通过比较路径长度与图的节点数量是否相等❶来初步判断路径的有效性。如果路径长度少于节点数，那么不可能访问了所有节点；如果路径长度多于节点数，则必然有节点被访问了不止一次。这一步也顺便处理了路径为空和图为空的特殊情况。

如果路径非空，代码会初始化一个布尔数组 visited 来跟踪每个节点是否已被访问，并用 prev_node 记录路径中的前一个节点❷。算法从路径的第一个节点开始，将其标记为已访问。

接下来的主要逻辑是一个 for 循环，用来遍历路径。在每一步中，算法会先检查前一个节点与当前节点之间是否存在边❸，然后检查当前节点是否已经访问过❹。如果这两个条件有一个不满足，说明该路径不是有效的哈密顿路径，立即返回 False。如果两个检查都通过，则将当前节点标记为已访问，并更新 prev_node 。当循环结束时，说明路径访问了图中所有节点且无重复，函数返回 True，表示该路径有效。

使用深度优先搜索查找哈密顿路径

虽然寻找哈密顿路径是一个 NP-困难（NP-hard） 问题，但我们仍然可以定义一种穷举搜索方法，尽管代价高昂，但它能够找到所有这样的路径。我们使用的是深度优先搜索（DFS）的变体，与传统 DFS 只访问每个节点一次不同，这里会探索经过某个节点的所有可能路径。

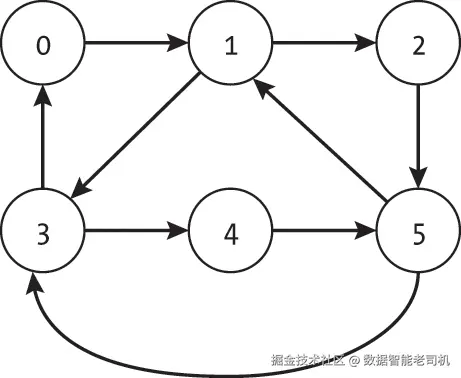
例如，图 18-3(a) 中的图有一条有效的哈密顿路径 [0, 1, 3, 2, 4]（见图 18-3(b)）。然而，第 4 章介绍的常规深度优先搜索并不会按这个顺序访问节点，而是会在访问节点 3 之前先访问节点 2。

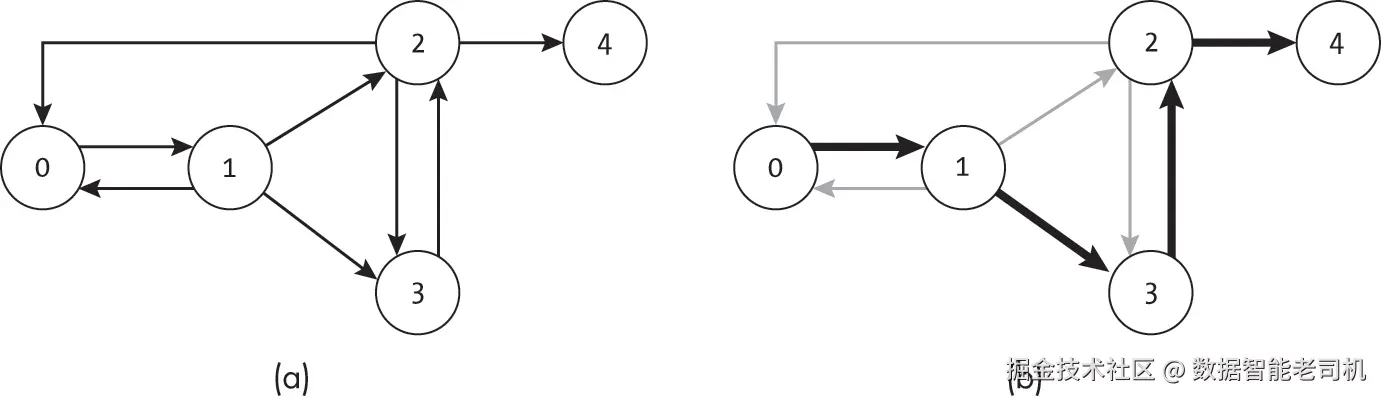
要找到有效的哈密顿路径，我们必须扩展深度优先搜索，使其具备回溯能力，从而尝试不同的路径。搜索在当前节点之后必须将已访问的节点重置为"未访问"状态，以便能够通过其他路径到达这些节点。

代码清单 18-1 展示了哈密顿路径深度优先搜索的实现，它在标准 DFS 的基础上做了少量修改：

def hamiltonian_dfs_rec(g: Graph, current: int, path: list,
                        seen: list) -> Union[list, None]: 
    path.append(current)
    seen[current] = True
  ❶ if len(path) == g.num_nodes:
        return path

    for edge in g.nodes[current].get_edge_list():
        n: int = edge.to_node
        if not seen[n]:
          ❷ result: Union[list, None] = hamiltonian_dfs_rec(g, n, path, seen)
            if result is not None:
                return result

  ❸ _ = path.pop()
    seen[current] = False
    return None

代码清单 18-1：递归搜索哈密顿路径的函数

函数 hamiltonian_dfs_rec() 接收以下参数：

• g：图对象
• current：当前节点索引
• path：当前路径（节点列表）
• seen：布尔列表，记录节点是否访问过

如果找到路径，则返回节点列表，否则返回 None。为了支持返回值的类型提示，需要从 Python 的 typing 库导入 Union。

算法首先将当前节点加入路径，并标记为已访问。然后检查是否已经访问了 g.num_nodes 个唯一节点❶，如果是，说明 path 是有效的哈密顿路径，直接返回它。

如果路径尚未完成，代码会遍历当前节点的所有出边，并对未访问的邻居递归调用❷。如果在这些探索中找到了有效的哈密顿路径（result 不为 None），则立即返回该路径。此时不会重置 seen 或 path，因为不需要再继续尝试其他路径。

如果遍历完所有出边仍未找到有效路径，算法会回溯 到上一个节点：将当前节点从 path 中移除，并将其标记为未访问❸，以便之后通过其他路径再次访问。最后返回 None，表示此分支未能找到路径。

我们还定义了一个包装函数，用于从每个可能的起始节点发起搜索：

def hamiltonian_dfs(g: Graph) -> Union[list, None]: 
    seen: list = [False] * g.num_nodes
    for start in range(g.num_nodes):
        path: Union[list, None] = hamiltonian_dfs_rec(g, start, [], seen)
        if path is not None:
            return path
    return None

hamiltonian_dfs() 函数将 seen 列表初始化为全 False，并用一个 for 循环从每个节点作为起点发起递归搜索。一旦找到路径（返回值非 None），就立即返回该路径；如果所有起点都未能找到有效的哈密顿路径，则返回 None。

图 18-4 展示了这个更新后的搜索过程。在图 18-4(a) 中访问节点 1 时，搜索有两个可选的下一步：节点 2 或节点 3。它首先探索节点 2，如图 18-4(b) 所示，但这会在节点 3 处陷入死胡同，导致节点 4 未被访问。由于无法访问节点 4，该路径无效，搜索必须回溯并尝试其他路径。

搜索回溯到节点 2，并将节点 3 标记为未访问状态，因为当前路径中已不再包含该节点。然后，搜索会考虑节点 2 的其他可行路径。由于节点 0 之前已经访问过，因此边 (2, 0) 被排除，只剩下边 (2, 4)，如图 18-4(c) 所示。不幸的是，沿着这条边会走到一个死胡同，无法访问节点 3，再次被阻断。

此时，搜索必须一路回溯到节点 1，并尝试通向节点 3 的路径，如图 18-4(d) 所示。它会将节点 2 和节点 4 都重置为未访问状态，并回到图 18-4(a) 所示的搜索状态。这使得搜索可以从节点 3 前往节点 2，再到节点 4。

然而，仅执行一次深度优先搜索可能还不够。与哈密顿回路不同，哈密顿路径的搜索结果会受到起始节点的影响。图 18-5 展示了一个图：如果从节点 1 出发，可以找到哈密顿路径 [1, 0, 2]；如果从节点 2 出发，可以找到哈密顿路径 [2, 0, 1]；但如果从节点 0 出发，则找不到任何哈密顿路径。

为了解决这个问题，我们可以针对每一个可能的起始节点分别运行一次深度优先搜索。搜索会一直进行，直到所有起始节点都尝试完，或者找到一条有效路径为止。

旅行商问题

旅行商问题（Traveling Salesperson Problem，TSP） 是在哈密顿回路 基础上的一种扩展，它引入了边权重的概念。该问题源于一个旅行推销员需要规划行程以访问多个城市的情境，其目标是找到一条路径，使得：

1. 从同一个节点出发并回到该节点；
2. 恰好访问每个节点一次；
3. 边权重（路径总花费）之和最小。

图 18-6 展示了一个示例图 (a) 以及通过该图的最低成本旅行商路线 (b)。即使在这样一个简单的图上，花几分钟手动尝试不同路径，也会很快发现问题的难度所在：即便是小规模的图，可能路径的数量也会呈爆炸式增长。

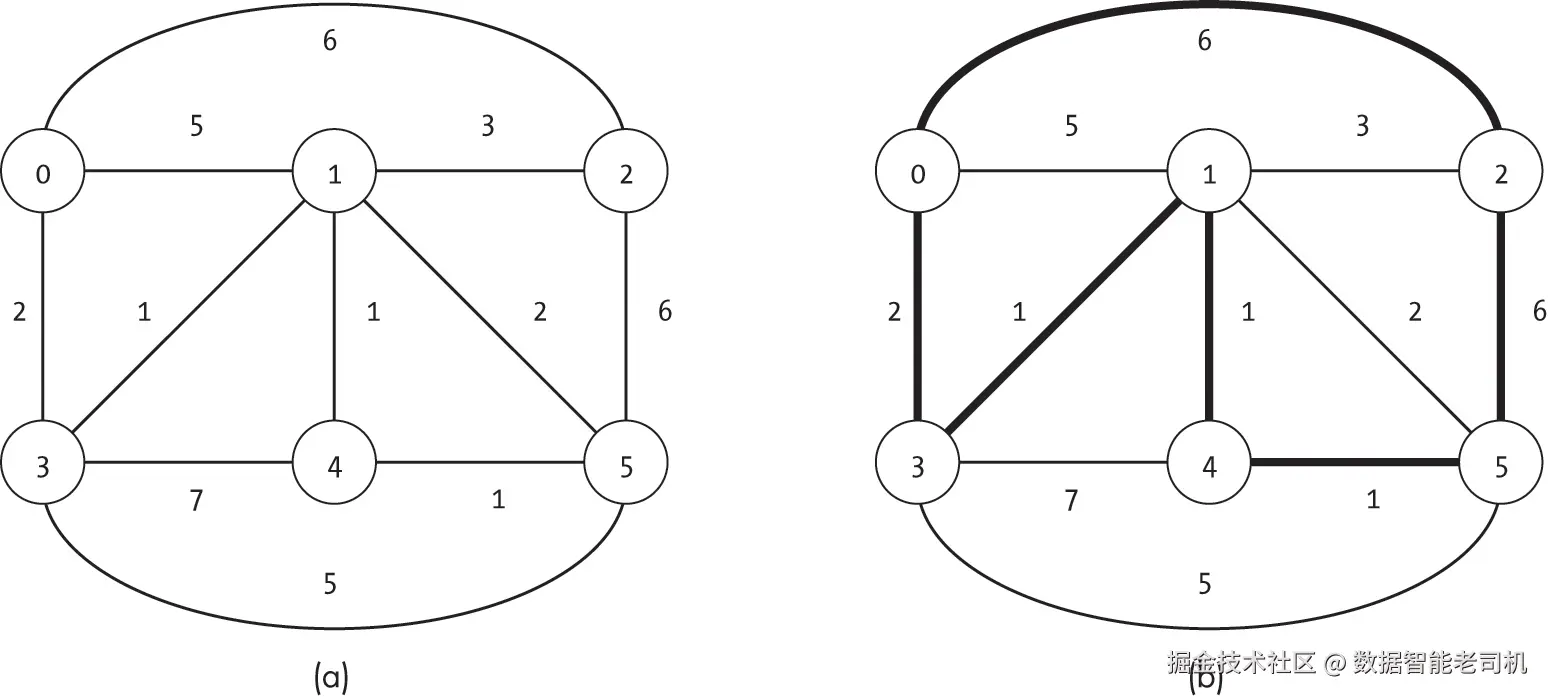
这个任务在现实世界的路径规划问题中有许多具体应用，使其在航运 和物流 等领域至关重要。正因如此，计算机科学家和数学家投入了大量时间和精力研究旅行商问题（TSP） ，并提出了多种方法，包括启发式搜索 和近似算法。在本节中，我们将在前面章节的方法基础上，研究一种基于**深度优先搜索（DFS）**的穷举解法。

深度优先搜索

我们可以直接将哈密顿路径的深度优先搜索算法改造，以支持路径成本计算。需要做三处改动：

1. 因为要找的是回路而不是路径，所以算法需要回到起点；
2. 不再在找到第一个有效结果时就停止，而是要继续搜索所有可能的哈密顿回路，以找到最低成本的那一个；
3. 在搜索过程中，需要记录目前找到的最佳路径 及其成本。

算法会在路径上执行深度优先搜索，在回溯时重置每个节点的 seen 状态，这样可以尝试从该节点出发的其他路径。每当递归到达终点并形成一个哈密顿回路时，就返回一份路径及其总成本的副本。调用方会比较每次递归返回的路径与成本，并保留最优解。

与哈密顿路径不同，TSP 的搜索可以从任意一个节点开始，因为最终结果是一个回路------无论起点选哪一个，回路的总成本都相同。

代码实现

我们将哈密顿路径的代码（见清单 18-1）改造，得到 TSP 的递归函数，如清单 18-2 所示：

def tsp_dfs_rec(g: Graph, path: list, seen: list, cost: float) -> tuple:
    current: int = path[-1]

    # ❶ 递归基：所有节点已访问
    if len(path) == g.num_nodes:
        last_edge: Union[Edge, None] = g.get_edge(current, path[0])
        if last_edge is not None:
            return (cost + last_edge.weight, path + [path[0]])
        else:
            return (math.inf, [])

    best_path: list = []
    best_score: float = math.inf
    for edge in g.nodes[current].get_edge_list():
        n: int = edge.to_node
        if not seen[n]:
            # ❷ 标记访问
            seen[n] = True
            path.append(n)

            # ❸ 递归探索
            result: tuple = tsp_dfs_rec(g, path, seen, cost + edge.weight)

            # ❹ 回溯
            seen[n] = False
            _ = path.pop()

            if result[0] < best_score:
                best_score = result[0]
                best_path = result[1]

    return (best_score, best_path)

清单 18-2：旅行商问题的递归搜索函数

tsp_dfs_rec() 接收图 g、当前路径 path、节点访问状态 seen 以及当前路径成本 cost。它先取当前节点 current（路径末尾的节点）。

在递归基 ❶ 中，如果所有节点都已访问，就检查能否从当前节点回到起点 path[0]：

• 如果可以，则返回总成本 和完整回路；
• 如果不行，则返回无限大成本，表示这不是一个有效回路。

如果还有未访问的节点，算法会遍历 current 的所有邻边，递归探索尚未访问的邻居节点 ❸。在探索前 ❷ 标记该节点已访问，并将其加入路径；探索完成后 ❹ 回溯，恢复访问状态并移除该节点。然后比较返回结果是否优于当前最佳解，如果更优，则更新。

外层封装函数

def tsp_dfs(g: Graph) -> tuple:
    if (g.num_nodes == 1):
        return (0.0, [0])

    seen: list = [False] * g.num_nodes
    path: list = [0]
    seen[0] = True

    return tsp_dfs_rec(g, path, seen, 0.0)

tsp_dfs() 先处理只有一个节点的特殊情况，返回 (0.0, [0])。否则，从节点 0 开始路径，标记为已访问，并调用递归搜索返回结果。

性能优化建议

清单 18-2 的递归函数是 TSP 的基础实现，可以通过剪枝提高效率，例如：

• 如果当前路径成本已超过当前最佳成本，则直接放弃该路径；
• 优先按照边权从小到大的顺序探索邻居节点，从而更快找到低成本解。

如前所述，TSP 的优化与启发式方法非常丰富，远超本章范围。

示例

图 18-7 展示了在图 18-6(a) 上运行该搜索的结果。每个子图表示一次递归到达基例时找到的哈密顿回路，其中路径以粗体标出，并在下方标注了成本。

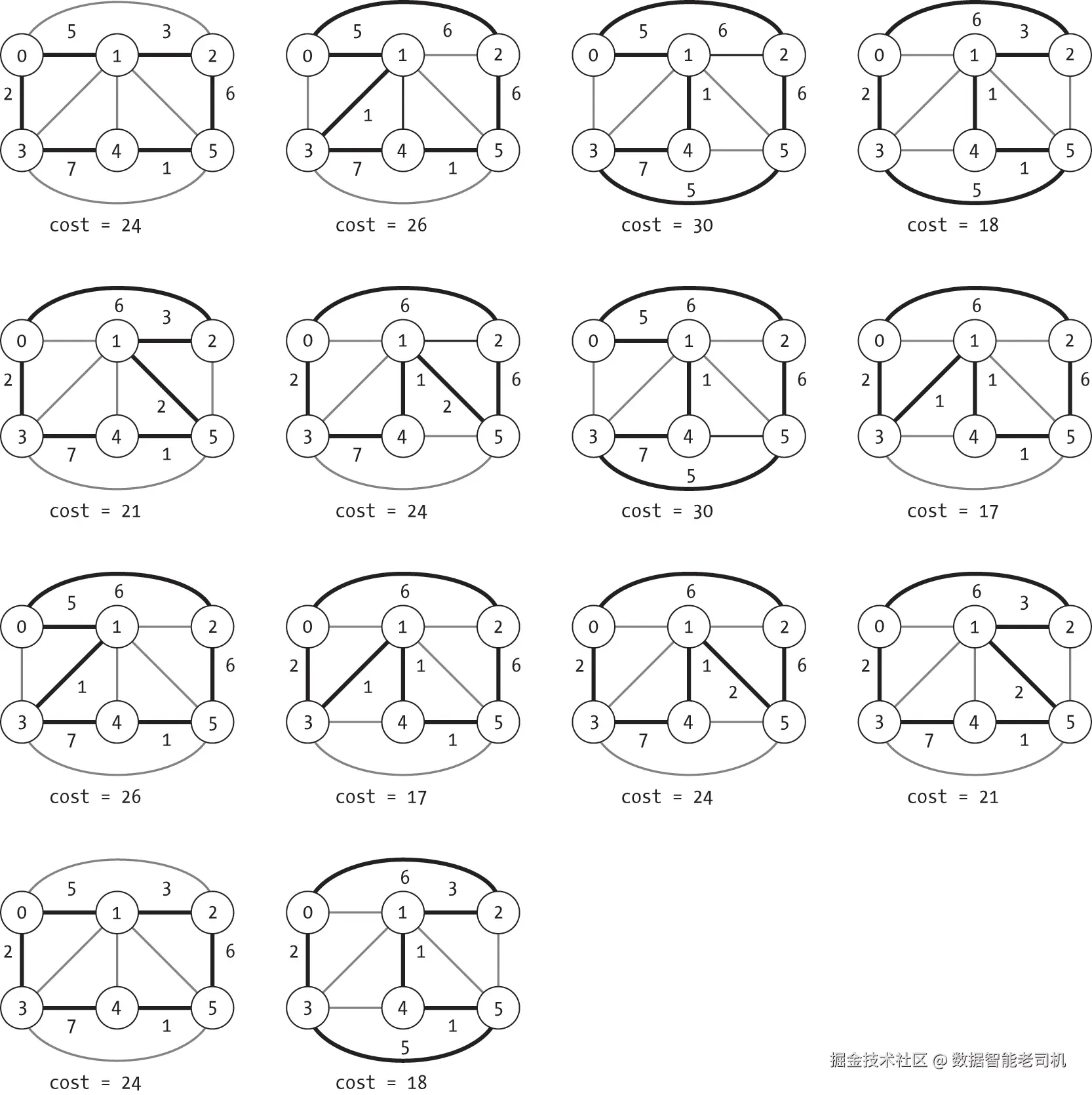
每条路径在图 18-7 中都会出现多次，因为算法会在两个方向上找到这个环路。

例如，第一个子图对应的路径是 [0, 1, 2, 5, 4, 3, 0]，而倒数第二个子图对应的路径是 [0, 3, 4, 5, 2, 1, 0]。

欧拉路径与欧拉回路

欧拉路径（Eulerian path）以数学家莱昂哈德·欧拉（Leonhard Euler）的名字命名，是图中一条恰好遍历每条边一次的路径。

我们可以把这个问题类比成一个高效的"橱窗购物"游客：为了逛遍城市里的所有商店，这位游客要寻找一条恰好经过每条道路一次的路线。他既不愿意错过任何潜在的好店（跳过一条路），也不愿意浪费时间去重复经过已经看过的商店。

欧拉回路（Eulerian cycle）是起点与终点相同的欧拉路径，非常适合那种既想每条路只走一次、又希望从酒店出发、最后回到酒店的游客。

注意

请记住，正如第 3 章所述，这里我们使用的是计算机科学教材中常见的路径定义，允许节点重复。这与图论中的严格定义不同，后者不允许节点重复。在图论中，这类问题通常被称为"欧拉迹（Eulerian trail）"的寻找。

图 18-8 展示了一个由六个节点组成的图上的欧拉回路。路径从节点 0 开始，为 [0, 1, 2, 5, 1, 3, 4, 5, 3, 0]。虽然它会多次经过某些节点，但它对九条边中的每一条都只遍历一次。游客可能会多次穿过同一个十字路口，但每条街上的橱窗只会看一次。

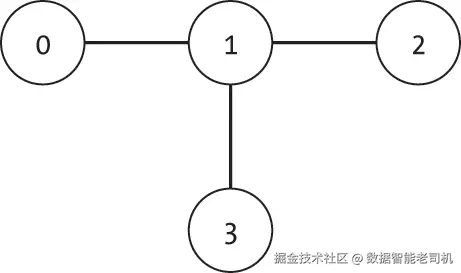
并非所有图都包含欧拉路径。图 18-9 展示了一个无法存在欧拉路径的无向图。

从节点 1 移动到任意其他节点后，搜索都需要使用同一条边返回到节点 1。由于节点 0、2 和 3 仅与节点 1 相连，任何经过所有边的路径都必须返回到节点 1。

莱昂哈德·欧拉提出了一种简单而有效的方法来测试一个连通的无向图是否存在欧拉环：

一个连通的无向图存在欧拉环，当且仅当所有节点的度数都是偶数。

利用这一测试，我们可以定义一个辅助函数，用于判断图是否既连通又存在欧拉环，如清单 18-3 所示：

def has_eulerian_cycle(g: Graph) -> bool: 
    ❶ components: list = dfs_connected_components(g)
    for i in range(g.num_nodes):
        ❷ if components[i] != 0:
            return False

        ❸ degree: int = g.nodes[i].num_edges()
        if i in g.nodes[i].edges:
            degree += 1
        if degree % 2 == 1:
            return False
    return True

清单 18-3：检查图是否连通并存在欧拉环

代码首先使用第 4 章的 dfs_connected_components() 函数标记每个节点的连通分量 ❶。然后通过 for 循环检查每个节点，确保它属于同一连通分量 ❷ 并且度数为偶数。

为了完整性，has_eulerian_cycle() 中的度数计算处理了无向自环的情况 ❸。正如第 2 章所述，无向图中形成自环的边在计算度数时会被计两次，因为它的两端都连接同一个节点。

如果代码发现有不连通的分量或度数为奇数的节点，会立即返回 False。如果检查完所有节点没有问题，则返回 True。

验证欧拉环路径

要判断一条路径是否为有效的欧拉环，需要检查每条边是否恰好使用一次。我们定义一个检查函数，该函数将路径表示为节点列表：

def is_eulerian_cycle(g: Graph, path: list) -> bool: 
    num_nodes: int = len(path)
    ❶ if num_nodes == 0:
        return g.num_nodes == 0

    ❷ used: dict = {}
    for node in g.nodes:
        for edge in node.get_edge_list():
            used[(edge.from_node, edge.to_node)] = False

    prev_node: int = path[0]
    for step in range(1, num_nodes):
        next_node: int = path[step]
        ❸ if not g.is_edge(prev_node, next_node):
            return False
        ❹ if used[(prev_node, next_node)]:
            return False

        ❺ used[(prev_node, next_node)] = True
        if g.undirected:
            used[(next_node, prev_node)] = True

        prev_node = next_node

    ❻ for value in used.values():
        if not value:
            return False
    ❼ return path[0] == path[-1]

is_eulerian_cycle() 代码首先检查空路径的边界情况，只有当图中没有节点时空路径才被认为有效 ❶。

如果路径包含边，代码会建立一个字典 used，将图中每条边映射为一个布尔值，表示该边是否已经被访问过 ❷。

代码主体通过 for 循环遍历路径，用前一个节点（prev_node）和当前节点（next_node）确定当前边。如果路径使用了不存在的边 ❸ 或已经被遍历的边 ❹，函数立即返回 False。否则，代码将边标记为已访问 ❺，对于无向图，需同时标记两个方向。

最后，代码检查所有边是否都已被访问，如果发现未访问的边则返回 False ❻。函数的最终检查是路径的起点和终点是否相同，从而确认路径是一个环 ❼。

使用 Hierholzer 算法寻找欧拉环

与本章前两个问题不同，寻找欧拉环并非 NP 难问题，存在一种高效方法可以在图中找到欧拉环。数学家 Carl Hierholzer 提出了一个算法，用于提取图中存在的欧拉环。Hierholzer 算法通过不断寻找未使用边的循环，并将这些循环从图中移除来操作。由于算法要求图必须存在欧拉环，因此我们使用欧拉度数测试（以及清单 18-3 的代码）预先检查图。

该方法的主要思路是：如果图存在欧拉环，我们可以将整个环构建为一系列可能较小的循环。我们称这些较小的循环为 子环，以区别于完整欧拉环。算法从在图中找到任意一个循环开始，并移除其边，这可能会在图中留下其他边。由于图有完整的欧拉环覆盖所有边，算法可以通过将剩余的边插入完整路径的方式，将每个以当前路径中某节点开始和结束的子环拼接进去，从而形成完整欧拉环。

图 18-10 展示了该算法的示例。在图 18-10(b) 中，搜索找到一个初始循环 [0, 1, 2, 5, 3, 0]，使用了五条边并访问了五个阴影节点。然后移除这些边，如图 18-10(c) 所示。

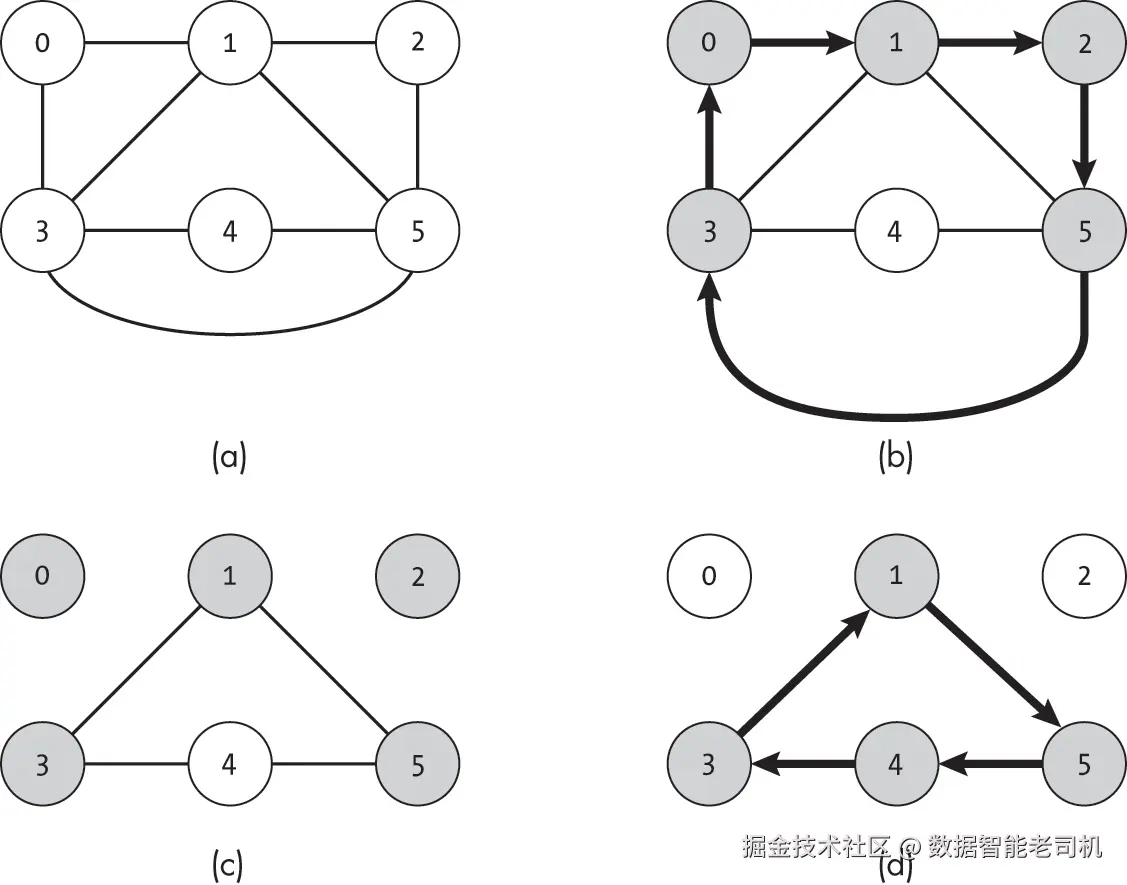
接下来，算法寻找一个从先前访问过的节点出发并返回该节点的循环，但路径上使用的是尚未遍历的边。图 18-10(d) 显示了循环 [1, 5, 4, 3, 1]。我们可以通过将这个新循环插入完整路径中节点 1 的位置，将其拼接为完整路径 [0, 1, 5, 4, 3, 1, 2, 5, 3, 0]。

根据算法选择下一个访问节点的不同方式，不同的实现可能最终探索不同的子环，并生成同一图的不同欧拉环。例如，本节的代码会按照图 18-10(a) 中节点的顺序，生成图 18-8 的最终欧拉环 [0, 1, 2, 5, 1, 3, 4, 5, 3, 0]。

要从图中提取欧拉环，我们必须沿着子环遍历图：

def hierholzers(g: Graph) -> Union[list, None]: 
    ❶ if not has_eulerian_cycle(g):
        return None

    g_r: Graph = g.make_copy()
    options: set = set([0])
    full_cycle: list = [0]

    while len(options) > 0:
        ❷ start: int = options.pop()
        current: int = start
        subcycle: list = [start]

        ❸ while current != start or len(subcycle) == 1:
            ❹ neighbor: int = list(g_r.nodes[current].edges.keys())[0]
            subcycle.append(neighbor)
            g_r.remove_edge(current, neighbor)

            ❺ new_num_edges: int = g_r.nodes[current].num_edges()
            if new_num_edges > 0:
                options.add(current)
            elif new_num_edges == 0 and current in options:
                options.remove(current)

            current = neighbor

        ❻ if g_r.nodes[start].num_edges() == 0 and start in options:
            options.remove(start)

        loc: int = full_cycle.index(start)
        ❼ full_cycle = full_cycle[0:loc] + subcycle + full_cycle[loc+1:]

    return full_cycle

代码首先使用清单 18-3 中的 has_eulerian_cycle() 函数确认图中存在欧拉环 ❶。如果检查失败，代码返回 None 表示不存在欧拉环。这里使用 typing 库的 Union 来支持多类型返回值的类型提示。

如果检查通过，代码初始化所需的数据结构，包括可修改的图副本 g_r、可用作子环起点的节点集合 options 以及用于跟踪构建中欧拉环的列表 full_cycle。代码通过沿着子环不断遍历，并将子环插入 full_cycle 中，逐步构建完整的欧拉环。

算法的主体是一个 while 循环，在存在已访问但仍有未使用边的节点时继续寻找新循环（即 options 非空）。options 集合提供了可开始新子环的节点列表。代码从 options 中弹出任意一个节点 ❷ 作为起点开始遍历循环。

代码通过内层 while 循环遍历新循环，直到完成环路并返回起点 ❸。循环条件还保证新循环至少走过一步才结束；如果 len(subcycle) == 1，循环继续执行，因为路径尚未移动。每一步，代码选择当前节点边字典的第一个键作为下一个访问节点（neighbor）❹，并将其添加到当前子环，同时从图副本中删除该边。

代码通过检查当前节点剩余的边数更新 options ❺。如果还有至少一条边，节点被添加到 options 表示存在其他路径可走；如果刚刚删除了该节点的最后一条边，则从 options 中移除该节点。内层循环结束后，如果起点已无剩余边，也从 options 中移除 ❻。

完成内层循环后，代码将子环插入 full_cycle ❼。为简化处理，这里使用线性时间查找（index()）并构建新的 full_cycle 副本。通过额外的记录，我们可以使用更高效的方法来降低该步骤的开销。

图 18-11 展示了 Hierholzer 算法在一个八节点图上的操作。图 18-11(a) 显示算法开始前图的状态、options 集合和 full_cycle 列表。后续子图展示了每次外层 while 循环迭代后的算法状态。该迭代中遍历并移除的边用粗体标出。

我们可以用一个城市旅游局官员规划全面游览的比喻来理解这个算法。他们的目标是设计一条路径，使每条街道仅走一次，让游客全面体验城市而不重复。官员选择城市的顶级酒店作为起点（节点 0）并开始出行。他们记录每条走过的街道，并访问尚未走过道路的交叉口。

图 18-11(b) 展示了旅游官员第一天的结果。他们走未走过的道路，完成一个小循环 [0, 1, 2, 0] 回到酒店。此时，从当前节点没有未走过的道路。尽管城市还有许多街道未探索，他们仍将已走过的道路 (0, 1)、(1, 2)、(2, 0) 从地图上标记为完成。他们也注意到，在交叉口（即节点）1 和 2，原本可以选择不同的道路。

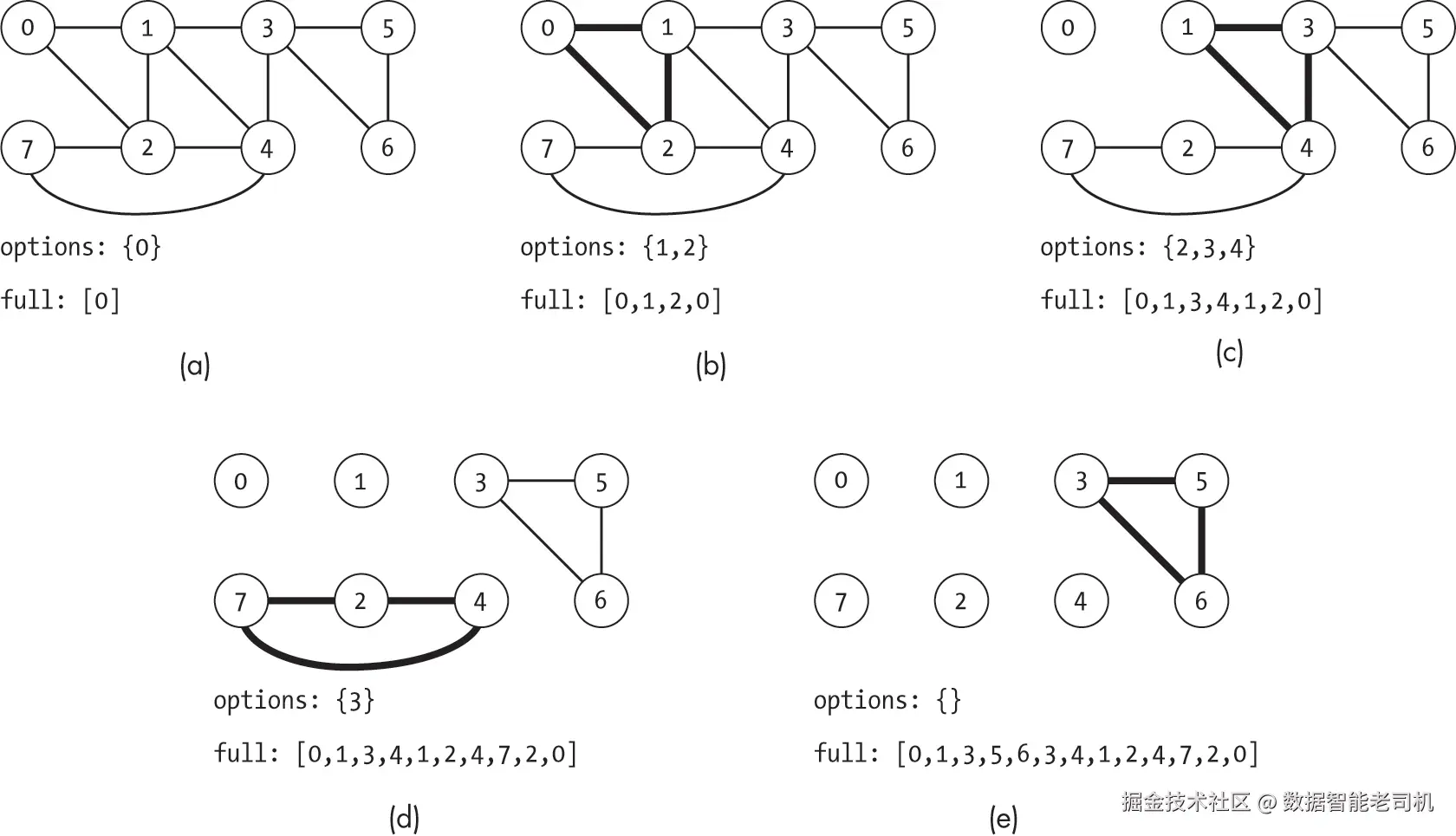
第二天，规划者前往一个还存在未走边的节点，从那里继续探索。如图 18-11(c) 所示，他们选择从节点 1 出发，因为它在前一次循环中可达，并且还有未探索的选项。他们完成了另一个小循环 [1, 3, 4, 1]，然后返回到节点 1，发现已经走完了所有相邻的街道。他们更新地图，删除已走的道路 (1, 3)、(3, 4) 和 (4, 1)，并记录下还有街道从交叉口 2、3 和 4 分支出去。当天的路径被拼接进昨天的路径，在节点 1 处形成一个组合路径 [0, 1, 3, 4, 1, 2, 0]。

第三天的过程类似，规划者从节点 2 出发，如图 18-11(d) 所示。他们完成循环 [2, 4, 7, 2]，删除已走的街道，并将组合路径扩展为 [0, 1, 3, 4, 1, 2, 4, 7, 2, 0]。在执行当天的巡游时，他们注意到已走完所有与节点 2 和 4 相邻的道路，因此从起始选项中删除这两个节点，只剩下节点 3。

最后一天从节点 3 出发，如图 18-12(e) 所示。规划者走过 [3, 5, 6, 3] 并将其拼接到组合路径中，形成一个欧拉回路 [0, 1, 3, 5, 6, 3, 4, 1, 2, 4, 7, 2, 0]。

为什么这很重要

本章讨论的三个问题------寻找哈密顿路径和欧拉路径，以及解决旅行商问题------在各种现实世界的规划和优化场景中都有明确应用。与前两章中从给定起点到指定终点寻找路径不同，这里讨论的问题旨在找到访问图中每个节点或每条边的路径。

这些问题为构建更复杂的任务提供了基础。我们可以在欧拉路径问题上加入成对顺序约束。例如，游客可能需要先访问城市的欢迎中心并购买票，才能乘坐贡多拉。公司可能会将城市分配给五个销售人员，需要同时分配城市和路径给每位员工。本章的三种问题形式只是我们可以提出的有趣且复杂问题的冰山一角。

本章的问题还表明，看似相似的问题在求解难度上可能存在巨大差异。虽然寻找欧拉路径和哈密顿路径在现实世界中有类似的类比，但它们的最坏情况计算成本差别显著。在考虑解决新问题的方法时，认识并理解这些差异非常重要。