DreamGym：通过经验合成实现代理学习的可扩展化

DreamGym：通过经验合成实现代理学习的可扩展化

今天，我们来聊聊一篇刚刚发布的论文：《Scaling Agent Learning via Experience Synthesis》（通过经验合成实现代理学习的扩展）。这篇论文由Meta Superintelligence Labs和FAIR团队主导，发表于2025年11月7日（arXiv:2511.03773v2）。如果你已经熟悉PPO（Proximal Policy Optimization）和GRPO（Group Relative Policy Optimization）等RL算法，这篇论文会特别对你的胃口。它提出了一种名为DreamGym的统一框架，旨在解决LLM代理在RL训练中的痛点：数据收集成本高、任务多样性不足、奖励信号不稳定，以及基础设施的复杂性。通过合成经验，DreamGym让代理训练变得高效、可扩展，甚至在sim-to-real转移中表现出色。

论文的核心洞见是：代理RL训练并不需要完美复制真实环境，而是需要多样、信息丰富且因果 grounded 的交互数据。DreamGym正是基于这个想法，构建了一个基于推理的经验模型，来生成合成 rollout，同时结合经验重放缓冲区和课程学习机制。接下来，我一步步拆解论文的内容，包括问题背景、方法细节和实验结果。走起！

RL在LLM代理中的瓶颈：为什么传统范式不work？

回想一下，LLM代理已经在web导航（Zhou et al., 2023）、具身控制（Shridhar et al.）和多轮工具使用（Yao et al., 2024）中大放异彩。但当我们转向"经验时代"（Silver and Sutton, 2025），用RL让代理通过自交互 bootstrapping 自我提升时，问题就来了。

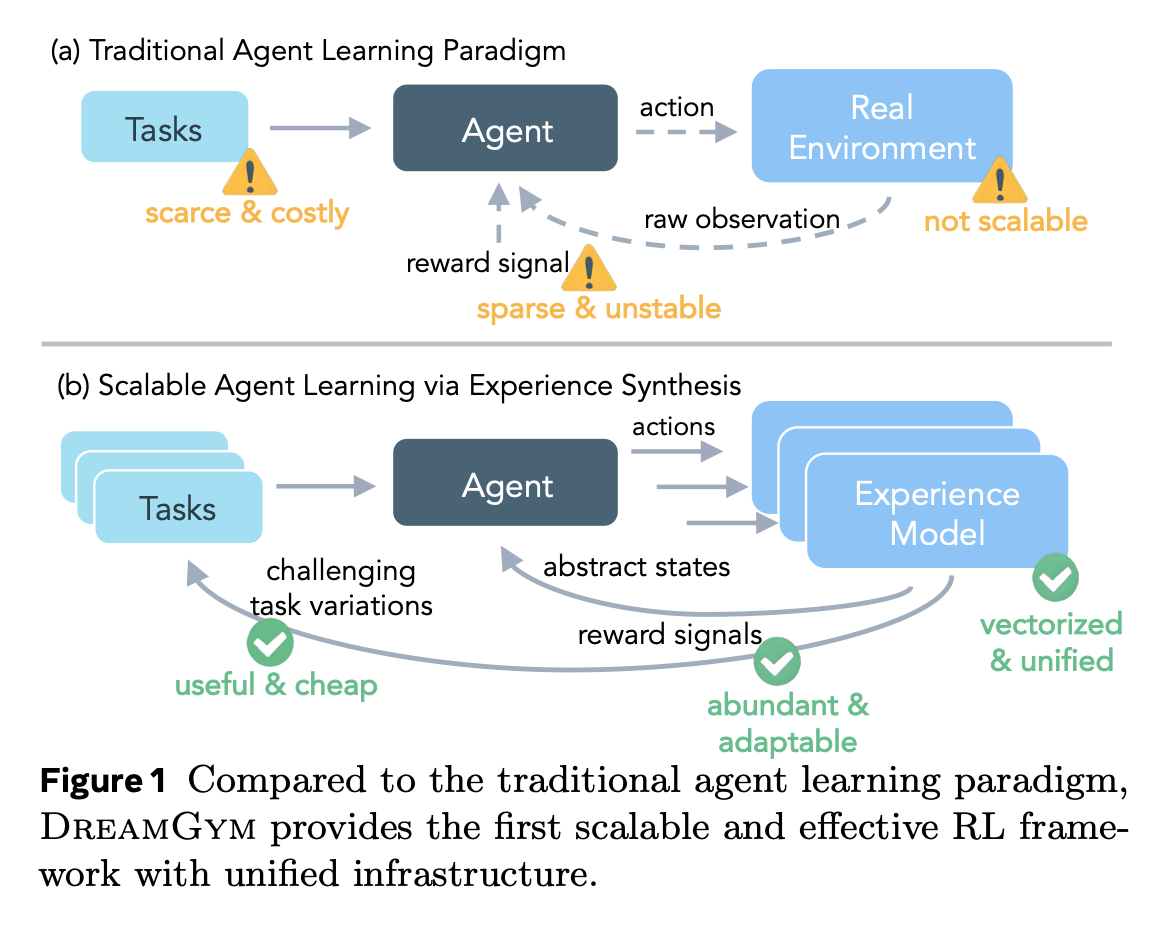
传统代理学习范式如图1(a)所示：代理与真实环境交互，产生 rollout，但面临四大挑战：

• 高成本 rollout：真实环境交互序列长、计算密集、奖励稀疏（Wei et al., 2025; Jiang et al., 2025）。
• 任务多样性不足：现有环境任务静态，扩展需人工验证（Xue et al., 2025），不利于目标条件RL（Eysenbach et al., 2018）。
• 奖励不稳定：动态环境（如web页面）产生噪声或虚假反馈（Deng et al., 2023），加上安全风险（如不可逆操作）。
• 基础设施复杂：依赖Docker或VM（Jimenez et al.; Xie et al., 2024b），大批量采样工程密集。

这些问题让RL在LLM代理上的实际应用举步维艰。论文提出DreamGym（如图1(b)），一个统一的合成经验框架，抽象环境动态到文本空间，生成廉价、多样且稳定的数据，支持在线RL训练。

预备知识：MDP与PPO/GRPO回顾

论文将代理学习形式化为MDP：M=(S,A,T,R,γ,ρ0)M = (S, A, T, R, \gamma, \rho_0)M=(S,A,T,R,γ,ρ0)，其中SSS是状态空间（e.g., 网页内容），AAA是动作空间（e.g., 点击UI），T:S×A→Δ(S)T: S \times A \to \Delta(S)T:S×A→Δ(S)是转移函数，R:S×A→RR: S \times A \to \mathbb{R}R:S×A→R是奖励，γ∈[0,1]\gamma \in [0,1]γ∈[0,1]是折扣因子，ρ0\rho_0ρ0包含初始任务τ0\tau_0τ0。

目标是优化策略πθ:S→Δ(A)\pi_\theta: S \to \Delta(A)πθ:S→Δ(A)，最大化期望累积奖励：
∇J(θ)=E(st,at)∼πθ[∇log⁡πθ(at∣st)⋅A^(st,at)], \nabla J(\theta) = \mathbb{E}{(s_t,a_t) \sim \pi\theta} \left[ \nabla \log \pi_\theta(a_t | s_t) \cdot \hat{A}(s_t, a_t) \right], ∇J(θ)=E(st,at)∼πθ[∇logπθ(at∣st)⋅A^(st,at)],

其中A^(st,at)\hat{A}(s_t, a_t)A^(st,at)是优势函数。

PPO（Schulman et al., 2017）用GAE计算优势：
A^tPPO=∑l=0K−1(γλ)l[rt+l+γV(st+l+1)−V(st+l)], \hat{A}^{\text{PPO}}t = \sum{l=0}^{K-1} (\gamma \lambda)^l [r_{t+l} + \gamma V(s_{t+l+1}) - V(s_{t+l})], A^tPPO=l=0∑K−1(γλ)l[rt+l+γV(st+l+1)−V(st+l)],
V(⋅)V(\cdot)V(⋅)由LLM近似，λ\lambdaλ平衡偏差-方差。

GRPO（Shao et al., 2024）扩展PPO，丢弃价值函数，用组内归一化奖励：
A^tGRPO=rt−Ei∈G[ri]stdi∈G[ri], \hat{A}^{\text{GRPO}}t = \frac{r_t - \mathbb{E}{i \in G} [r_i]}{\text{std}_{i \in G} [r_i]}, A^tGRPO=stdi∈G[ri]rt−Ei∈G[ri],

其中GGG是同一任务的响应组。这更易扩展，但样本效率可能稍低。DreamGym与这些算法正交，焦点是合成高质量经验。

DreamGym的核心：三个关键组件

DreamGym围绕三个组件构建（如图2）：（1）推理经验模型MexpM_{\text{exp}}Mexp，（2）经验重放缓冲区，（3）课程任务生成器。它们协同生成多样 rollout，支持RL训练。

1. 推理经验模型：抽象文本空间中的高效合成

传统世界模型（如Dreamer, Hafner et al., 2020）在像素空间昂贵。DreamGym用LLM-based MexpM_{\text{exp}}Mexp在抽象文本状态SSS中工作，丢弃无关细节（e.g., HTML标签，只保留元素列表）。这让训练高效，只需少量离线轨迹（如WebArena基准）。

推理过程 ：给定当前状态-动作对、历史{(si,ai)}i=0t\{(s_i, a_i)\}{i=0}^t{(si,ai)}i=0t、任务τ\tauτ和top-k相似演示{dj}j=1k\{d_j\}{j=1}^k{dj}j=1k（从缓冲区检索，相似度cos⁡(ϕ(st,at),ϕ(si,ai))\cos(\phi(s_t, a_t), \phi(s_i, a_i))cos(ϕ(st,at),ϕ(si,ai))），模型用CoT生成下一状态和奖励：
(st+1,rt+1)=Mexp(Rt∣{(si,ai)}i=0t,{dj}j=1k,τ), (s_{t+1}, r_{t+1}) = M_{\text{exp}} \left( R_t \mid \{(s_i, a_i)\}{i=0}^t, \{d_j\}{j=1}^k, \tau \right), (st+1,rt+1)=Mexp(Rt∣{(si,ai)}i=0t,{dj}j=1k,τ),
RtR_tRt是显式推理轨迹。奖励基于结局：成功 r=1 （最终步），否则（最终步），否则（最终步），否则 r=0 （Feng et al., 2025）。这确保因果一致，避免幻觉。

训练 ：用SFT蒸馏离线数据D={(st,at,st+1,rt+1)}D = \{(s_t, a_t, s_{t+1}, r_{t+1})\}D={(st,at,st+1,rt+1)}，每个转移标注CoT Rt∗R_t^*Rt∗：
LSFT=E(st,at,st+1,Rt∗)∼D[−log⁡Pθ(Rt∗∣st,at,Ht,Dk)−log⁡Pθ(st+1∣st,at,Rt∗,Ht,Dk)], \mathcal{L}{\text{SFT}} = \mathbb{E}{(s_t,a_t,s_{t+1},R_t^*) \sim D} \left[ -\log P_\theta(R_t^* | s_t, a_t, H_t, D_k) - \log P_\theta(s_{t+1} | s_t, a_t, R_t^*, H_t, D_k) \right], LSFT=E(st,at,st+1,Rt∗)∼D[−logPθ(Rt∗∣st,at,Ht,Dk)−logPθ(st+1∣st,at,Rt∗,Ht,Dk)],
HtH_tHt是历史，DkD_kDk是检索演示。这让模型不仅模仿专家，还学会泛化推理。

2. 经验重放缓冲区：离线+在线共进化

缓冲区从离线真实数据初始化，存储轨迹。交互中检索相似轨迹指导MexpM_{\text{exp}}Mexp，减少噪声。新合成轨迹在线更新缓冲区，与代理策略共进化，确保数据对齐。

3. 课程任务生成器：奖励熵驱动的适应性

任务扩展成本高，DreamGym用MtaskM_{\text{task}}Mtask（共享MexpM_{\text{exp}}Mexp参数）从种子任务生成变体：
τt=Mtask({τit−1}i=1m). \tau_t = M_{\text{task}} \left( \{\tau_i^{t-1}\}_{i=1}^m \right). τt=Mtask({τit−1}i=1m).

种子选高价值任务：组奖励熵
Vτ=1n∑i=1n(ri−rˉ)2,rˉ=1n∑i=1nri, V_\tau = \frac{1}{n} \sum_{i=1}^n (r_i - \bar{r})^2, \quad \bar{r} = \frac{1}{n} \sum_{i=1}^n r_i, Vτ=n1i=1∑n(ri−rˉ)2,rˉ=n1i=1∑nri,

高熵表示任务可行但挑战（成功/失败平衡，Gao et al., 2025）。用超参λ\lambdaλ控制合成任务比例，避免分布偏移。

训练循环：从种子任务开始，代理-模型交互生成 rollout，用PPO/GRPO更新策略。然后生成新任务变体，循环至收敛。附录B.1证明了合成经验下的策略改进下界（信任域假设）。

实验亮点：30%+提升，sim-to-real神器

论文在多样环境和代理骨架上评估DreamGym。

• 非RL-ready任务（如WebArena）：DreamGym是唯一可行RL方案，提升30%+ vs. 基线/SOTA。
• RL-ready但昂贵环境：纯合成交互匹配GRPO/PPO性能，无需外部交互。
• DreamGym-S2R (sim-to-real)：先合成训练，再转移真实环境，提升40%+，仅用<10%真实数据。作为warm-start策略，完美！

这些结果证明DreamGym在任务/奖励稀疏中卓越，启用高效合成RL和泛化转移。

结语：DreamGym的潜力与启发

DreamGym不是简单模拟器，而是RL-ready的统一基础设施，解决LLM代理训练的 scalability 瓶颈。它与AgentSynth（Xie et al., 2025）或UI-Simulator（Wang et al., 2025b）不同，提供完整工具链：多样任务生成、一致 rollout 和丰富奖励。

如果你在搞代理RL，这框架值得一试！代码/细节见论文附录。欢迎评论你的想法------PPO vs. GRPO在合成数据上，谁更香？下期见~

（参考：arXiv:2511.03773v2，Meta团队，2025）

DreamGym中经验模型的核心公式详解

在上面，简要介绍了DreamGym框架的推理经验模型（Reasoning Experience Model, MexpM_{\text{exp}}Mexp），包括其推理过程和训练损失函数。这些公式是DreamGym的核心，体现了如何通过链式思考（Chain-of-Thought, CoT）在抽象文本空间中生成一致的合成经验，从而支持高效的RL训练。如果你熟悉PPO和GRPO的策略梯度优化（∇J(θ)=E[∇log⁡πθ(at∣st)⋅A^(st,at)]\nabla J(\theta) = \mathbb{E} [\nabla \log \pi_\theta(a_t | s_t) \cdot \hat{A}(s_t, a_t)]∇J(θ)=E[∇logπθ(at∣st)⋅A^(st,at)]），这些公式可以看作是上游数据生成机制：它们确保生成的(st+1,rt+1)(s_{t+1}, r_{t+1})(st+1,rt+1)对下游优势估计A^\hat{A}A^更稳定、信息丰富。下面，我一步步拆解这些公式，结合论文的上下文（从提供的PDF页面1-6），解释其数学含义、设计动机、计算细节，以及与RL训练的关联。解释会保持严谨，但易懂------假设你已知MDP基础（M=(S,A,T,R,γ,ρ0)M = (S, A, T, R, \gamma, \rho_0)M=(S,A,T,R,γ,ρ0)）。

1. 推理过程公式：生成下一状态和奖励

论文的核心公式是经验模型的推理 rollout 生成 ：
(st+1,rt+1)=Mexp(Rt∣{(si,ai)}i=0t,{dj}j=1k,τ), (s_{t+1}, r_{t+1}) = M_{\text{exp}} \left( R_t \mid \{(s_i, a_i)\}{i=0}^t, \{d_j\}{j=1}^k, \tau \right), (st+1,rt+1)=Mexp(Rt∣{(si,ai)}i=0t,{dj}j=1k,τ),

其中：

• 左侧输出 ：(st+1,rt+1)(s_{t+1}, r_{t+1})(st+1,rt+1) 是代理在时间t+1t+1t+1的下一状态（抽象文本描述，如网页元素的精炼列表）和奖励信号。状态st+1∈Ss_{t+1} \in Sst+1∈S（抽象空间，e.g., "订单表显示了1月食品支出150"），奖励150"），奖励150"），奖励r_{t+1} \in {0, 1}$（二元结局奖励，详见下文）。
• 右侧条件输入 ：
  • {(si,ai)}i=0t\{(s_i, a_i)\}_{i=0}^t{(si,ai)}i=0t：交互历史轨迹（长度t+1t+1t+1），确保状态一致性（e.g., 避免突然"跳跃"到无关页面）。
  • {dj}j=1k\{d_j\}_{j=1}^k{dj}j=1k：从经验重放缓冲区检索的top-kkk相似演示（kkk通常小，如5-10）。相似度用余弦距离cos⁡(ϕ(st,at),ϕ(si,ai))\cos(\phi(s_t, a_t), \phi(s_i, a_i))cos(ϕ(st,at),ϕ(si,ai))计算，其中ϕ(⋅)\phi(\cdot)ϕ(⋅)是任意语义编码器（e.g., LLM嵌入）。这注入"记忆"，减少幻觉（hallucination），类似于RAG（Retrieval-Augmented Generation）。
  • τ\tauτ：当前任务指令（自然语言，e.g., "查询1月中食品支出"），条件化模型对动作的解释。
  • RtR_tRt：显式CoT推理轨迹（文本链），由MexpM_{\text{exp}}Mexp先生成，用于指导输出。例如，RtR_tRt可能描述："用户点击'我的账户'链接 → 加载订单页 → 提取食品类别数据 → 验证任务进度，未完成"。

设计动机 ：传统RL rollout依赖真实环境T(st,at)→st+1T(s_t, a_t) \to s_{t+1}T(st,at)→st+1，但成本高且不稳定（稀疏奖励、噪声）。这里，MexpM_{\text{exp}}Mexp（LLM参数化）在抽象SSS中模拟TTT和RRR，通过CoT确保因果一致 （causal grounding）：输出反映动作的真实后果，而非随机。论文强调，这不需要像素级真实（不像Dreamer的像素世界模型），只需"足够多样、信息丰富"的数据，就能为PPO/GRPO提供高质量轨迹ϵ={τ0∣s0,a0,... }\epsilon = \{\tau_0 | s_0, a_0, \dots \}ϵ={τ0∣s0,a0,...}。

计算细节：

• 步骤1 ：输入历史+检索+τ\tauτ到MexpM_{\text{exp}}Mexp，生成RtR_tRt（自回归文本生成，e.g., Llama-3提示："基于历史和演示，逐步推理动作ata_tat的影响"）。
• 步骤2 ：用RtR_tRt条件化生成(st+1,rt+1)(s_{t+1}, r_{t+1})(st+1,rt+1)。如果ata_tat无效（e.g., 点击不存在链接），RtR_tRt推导出失败状态st+1s_{t+1}st+1（e.g., "错误页"）和rt+1=0r_{t+1}=0rt+1=0；反之，推进进度。
• 奖励设计 （论文4.1.1，引用Feng et al., 2025）：结局导向（outcome-based），仅在最终步（done=True）成功时r=1r=1r=1，否则全程r=0r=0r=0。这简化稀疏奖励问题，与GRPO的组归一化A^tGRPO=(rt−μG)/σG\hat{A}^{\text{GRPO}}_t = (r_t - \mu_G)/\sigma_GA^tGRPO=(rt−μG)/σG兼容（组GGG内平衡成功/失败，提升熵）。
• 与RL关联 ：生成的轨迹直接喂入PPO的GAE（A^tPPO=∑(γλ)l[rt+l+γV(st+l+1)−V(st+l)]\hat{A}^{\text{PPO}}t = \sum (\gamma \lambda)^l [r{t+l} + \gamma V(s_{t+l+1}) - V(s_{t+l})]A^tPPO=∑(γλ)l[rt+l+γV(st+l+1)−V(st+l)]）或GRPO，避免真实环境的噪声。实验显示，这匹配真实PPO性能，但零外部交互。

潜在局限 ：CoT依赖LLM质量，若ϕ(⋅)\phi(\cdot)ϕ(⋅)编码弱，检索可能偏差；论文用小kkk和历史窗口缓解。

2. 奖励信号的二元设计：r=1r = 1r=1（成功，最终步）或r=0r = 0r=0（否则）

这不是独立公式，而是嵌入上式的约束（rt+1∈{0,1}r_{t+1} \in \{0,1\}rt+1∈{0,1}，仅终端状态触发111）。动机 ：LLM代理任务多为长序列（long-horizon），中间奖励稀疏易导致崩溃（credit assignment难）。二元设计聚焦"任务完成"，简化A^\hat{A}A^计算，尤其GRPO（组内标准化奖励，无需V(⋅)V(\cdot)V(⋅)）。

计算 ：RtR_tRt评估任务τ\tauτ进度，若轨迹结束且τ\tauτ满足（e.g., 提取正确支出），r=1r=1r=1；否则000。这确保"因果一致，避免幻觉"------e.g., 模型不会随意给高奖励。

与RL关联 ：在高熵任务（Vτ=1n∑(ri−rˉ)2>0V_\tau = \frac{1}{n} \sum (r_i - \bar{r})^2 > 0Vτ=n1∑(ri−rˉ)2>0）中，平衡成功/失败，促进探索（Eysenbach et al., 2018）。PPO用此累积A^\hat{A}A^，GRPO用组rˉ,σr\bar{r}, \sigma_rrˉ,σr归一化，提升稳定性。

3. 训练公式：SFT损失函数

经验模型MexpM_{\text{exp}}Mexp通过监督微调（SFT）从离线数据D={(st,at,st+1,rt+1)}D = \{(s_t, a_t, s_{t+1}, r_{t+1})\}D={(st,at,st+1,rt+1)}蒸馏知识：
LSFT=E(st,at,st+1,Rt∗)∼D[−log⁡Pθ(Rt∗∣st,at,Ht,Dk)−log⁡Pθ(st+1∣st,at,Rt∗,Ht,Dk)], \mathcal{L}{\text{SFT}} = \mathbb{E}{(s_t,a_t,s_{t+1},R_t^*) \sim D} \left[ -\log P_\theta(R_t^* | s_t, a_t, H_t, D_k) - \log P_\theta(s_{t+1} | s_t, a_t, R_t^*, H_t, D_k) \right], LSFT=E(st,at,st+1,Rt∗)∼D[−logPθ(Rt∗∣st,at,Ht,Dk)−logPθ(st+1∣st,at,Rt∗,Ht,Dk)],

其中：

• 期望E∼D\mathbb{E} \sim DE∼D：从离线轨迹数据集采样（e.g., WebArena基准，小型公开数据，论文称"高度样本高效"）。
• 每个转移标注 ：用LLM（提示见附录C.1）为(st,at)→(st+1,rt+1)(s_t, a_t) \to (s_{t+1}, r_{t+1})(st,at)→(st+1,rt+1)生成 ground-truth CoT Rt∗R_t^*Rt∗（e.g., "动作点击订单 → 因任务τ\tauτ，状态更新为表提取 → 奖励0，因未终"）。
• 联合损失 ：两项负对数似然（cross-entropy）：
  • 第一项−log⁡Pθ(Rt∗∣st,at,Ht,Dk)-\log P_\theta(R_t^* | s_t, a_t, H_t, D_k)−logPθ(Rt∗∣st,at,Ht,Dk)：生成忠实推理（faithful reasoning）。HtH_tHt是历史（类似上式），DkD_kDk是检索演示（训练时也用RAG模拟在线）。
  • 第二项−log⁡Pθ(st+1∣st,at,Rt∗,Ht,Dk)-\log P_\theta(s_{t+1} | s_t, a_t, R_t^*, H_t, D_k)−logPθ(st+1∣st,at,Rt∗,Ht,Dk)：条件于Rt∗R_t^*Rt∗预测下一状态，确保CoT指导输出一致。
• 参数θ\thetaθ ：MexpM_{\text{exp}}Mexp的LLM权重（共享MtaskM_{\text{task}}Mtask）。

设计动机 ：不像像素世界模型需海量数据，抽象SSS让训练只需少量DDD（e.g., 公共基准轨迹）。联合目标让模型不只模仿专家（imitation），还学会泛化推理 （generalize）：Rt∗R_t^*Rt∗解释因果（"为什么ata_tat导致st+1s_{t+1}st+1"），桥接离线到在线RL。

计算细节：

• 数据准备 ：对DDD中每个转移，LLM标注Rt∗R_t^*Rt∗（一次性，成本低）。
• 优化 ：标准SFT（e.g., AdamW），焦点是token-level交叉熵。PθP_\thetaPθ是自回归概率（LLM输出分布）。
• 效率 ：论文4.1.2强调，只需"abundant offline trajectory datasets"如WebArena；在线时，缓冲区更新DDD，让MexpM_{\text{exp}}Mexp与代理πθ\pi_\thetaπθ共进化。

与RL关联 ：训练好的MexpM_{\text{exp}}Mexp生成轨迹ϵ\epsilonϵ，喂入PPO/GRPO更新πθ\pi_\thetaπθ。这放大RL效果：合成数据多样（via 课程），稳定（CoT），信息丰富（检索），实验中sim-to-real提升40%+（用<10%真实数据）。

这些公式的整体作用与启发

• 统一流程 （图2）：种子任务τ0\tau_0τ0 → 代理选ata_tat → MexpM_{\text{exp}}Mexp用上式生成(st+1,rt+1)(s_{t+1}, r_{t+1})(st+1,rt+1) → 更新缓冲 → 高熵任务变体（VτV_\tauVτ选）→ 循环RL。
• 理论支撑 ：附录B.1证明合成经验下策略改进下界（trust-region假设下，E[∇J]≥ϵ\mathbb{E}[\nabla J] \geq \epsilonE[∇J]≥ϵ）。
• 实践价值：对PPO/GRPO用户，这提供"廉价warm-start"------纯合成训练匹配真实性能，转移时少量finetune。

DreamGym中的课程任务生成（Curriculum-based Task Generation）详解

大家好！在上两篇关于《Scaling Agent Learning via Experience Synthesis》（通过经验合成实现代理学习的扩展）论文的讨论中，我们先介绍了整体框架，然后深挖了推理经验模型的公式。今天，我们聚焦论文的4.2节：基于课程的任务生成 （Curriculum-based Task Generation）。这个机制是DreamGym的亮点之一，它解决了RL训练中任务多样性不足的痛点：传统方法扩展任务需大量人工验证（Zhou et al., 2025），成本高且不适应动态代理策略。DreamGym通过经验模型MexpM_{\text{exp}}Mexp的变体MtaskM_{\text{task}}Mtask，自动生成适应性任务变体，实现在线课程学习（online curriculum learning），让代理逐步面对更具挑战性的问题，从而提升知识获取效率。

如果你熟悉PPO或GRPO，这部分特别实用：它确保生成的合成任务与下游优势估计A^\hat{A}A^对齐，提供高信息增益（information gain）的轨迹，避免训练崩溃（training collapse）。下面，我从动机、核心公式、选择机制、稳定性设计，到与RL的整合，一步步拆解。解释基于论文提供的抽象状态空间SSS和MDP形式化（M=(S,A,T,R,γ,ρ0)M = (S, A, T, R, \gamma, \rho_0)M=(S,A,T,R,γ,ρ0)），公式会用LaTeX格式呈现（单符号用'，完整公式用`，完整公式用'，完整公式用$）。

1. 动机：为什么需要课程任务生成？

RL代理（如LLM-based）需要多样、课程对齐的任务指令来获取知识（Zhou et al., 2025）。但现实中：

• 扩展成本高：验证新任务的可行性需人工努力（e.g., 检查web环境是否支持），尤其在目标域（如WebArena）中。
• 静态任务不足：现有环境任务有限，无法支持有效探索（Eysenbach et al., 2018）。
• 适应性差 ：代理策略πθ\pi_\thetaπθ更新后，原任务可能太简单，导致信息增益低；或太难，导致失败率高，奖励稀疏。

DreamGym的创新：利用经验模型的合成多轮转移能力 （synthetic multi-turn transitions），从少量种子任务（seed tasks）生成变体，无需真实环境验证。这构建了一个自适应课程：代理能力提升时，任务难度同步递增，促进渐进学习（progressive learning）。结果？实验中，DreamGym在高熵任务上提升代理探索，sim-to-real转移性能+40%（仅用<10%真实数据）。

2. 核心公式：任务生成过程

任务生成由MtaskM_{\text{task}}Mtask（参数共享MexpM_{\text{exp}}Mexp，复用CoT推理能力）驱动，从上一迭代的mmm个种子任务{τit−1}i=1m\{\tau_i^{t-1}\}{i=1}^m{τit−1}i=1m产生新任务τt\tau_tτt：
τt=Mtask({τit−1}i=1m). \tau_t = M{\text{task}} \left( \{\tau_i^{t-1}\}_{i=1}^m \right). τt=Mtask({τit−1}i=1m).

• 输入 ：{τit−1}i=1m\{\tau_i^{t-1}\}_{i=1}^m{τit−1}i=1m 是上一轮高价值种子（详见下节），自然语言描述（e.g., "查询1月中食品支出"）。
• 输出 ：τt\tau_tτt 是变体（e.g., "查询2月中食品支出，并比较增长率"），保持域内一致，但增加复杂度（如多步推理）。
• 共享参数 ：MtaskM_{\text{task}}Mtask继承MexpM_{\text{exp}}Mexp的θ\thetaθ，利用CoT生成"渐进挑战"（progressively challenging variations）。这高效：无需额外训练，只需提示调整（e.g., "基于种子，生成更难变体"）。

设计洞见 ：种子选择基于双标准：

1. 足够挑战当前πθ\pi_\thetaπθ：最大化信息增益（maximizing information gain），避免过易任务。
2. 定义良好：过滤不现实/畸形任务（unrealistic or malformed），确保可合成。

这让生成过程自举（self-bootstrapping）：从少量种子（e.g., 10-20个初始任务）扩展到数千变体，支持大规模RL。

3. 种子选择机制：组奖励熵（Group-based Reward Entropy）

为量化"高价值"种子，论文引入奖励熵作为价值度量 VτV_\tauVτ，捕捉任务的挑战性与可行性 。对于任务τ\tauτ，从nnn次 rollout（在组GGG内）获取结局奖励ri∈{0,1}r_i \in \{0,1\}ri∈{0,1}（二元：成功=1，否则=0），定义：
Vτ=1n∑i=1n(ri−rˉ)2,rˉ=1n∑i=1nri. V_\tau = \frac{1}{n} \sum_{i=1}^n (r_i - \bar{r})^2, \quad \bar{r} = \frac{1}{n} \sum_{i=1}^n r_i. Vτ=n1i=1∑n(ri−rˉ)2,rˉ=n1i=1∑nri.

• 数学含义 ：VτV_\tauVτ 是奖励的样本方差 （sample variance），度量不确定性（entropy）。rˉ\bar{r}rˉ是组均值，(ri−rˉ)2(r_i - \bar{r})^2(ri−rˉ)2惩罚偏差。
  • Vτ=0V_\tau = 0Vτ=0：全成功（太易，无学习价值）或全失败（不可行）。
  • Vτ>0V_\tau > 0Vτ>0：混合成功/失败，表示可行但挑战（feasible yet challenging）。
  • 最大熵 ：Vτ≈0.25V_\tau \approx 0.25Vτ≈0.25（Bernoulli分布，p=0.5p=0.5p=0.5时方差最大），成功/失败平衡，提供最大信用分配增益（credit assignment gain）。
• 组GGG定义 ：
  • GRPO模式 ：GGG直接是训练组（同一τ\tauτ的响应采样），兼容组相对优势A^tGRPO=(rt−Ei∈G[ri])/stdi∈G[ri]\hat{A}^{\text{GRPO}}t = (r_t - \mathbb{E}{i \in G}[r_i]) / \text{std}_{i \in G}[r_i]A^tGRPO=(rt−Ei∈G[ri])/stdi∈G[ri]。
  • PPO模式 ：先用语义嵌入器（semantic embedder，如BERT）聚类任务，每个簇形成GGG，再生成变体。确保组内相似，避免分布偏移。
• 与LLM学习一致 ：高熵任务对应"中等难度"（intermediate difficulty），LLM从中获益最多（Gao et al., 2025）。e.g., 在WebArena，VτV_\tauVτ高的任务如"复杂查询+分页"比简单"点击登录"更有效。

计算细节：

• 采样nnn ：小批量（e.g., 10-50），用当前πθ\pi_\thetaπθ在DreamGym中 rollout（零成本合成）。
• 阈值选择 ：选Vτ>θV_\tau > \thetaVτ>θ（θ\thetaθ小正数）的任务作为种子，喂入MtaskM_{\text{task}}Mtask生成变体。
• 为什么熵？：非零方差信号代理看到"边界案例"（edge cases），提升泛化（generalization），一致于探索理论（Eysenbach et al., 2018）。

4. 稳定性设计：超参数λ\lambdaλ的角色

为防训练不稳（e.g., 过度偏向合成任务，导致原分布覆盖不足），引入λ∈[0,1]\lambda \in [0,1]λ∈[0,1]：每迭代采样合成任务的比例上限λ\lambdaλ。

• 效果 ：保留(1−λ)(1-\lambda)(1−λ)原任务覆盖，确保广度；λ\lambdaλ引导探索πθ\pi_\thetaπθ弱点（weakness regions），实现课程平衡（curriculum balance）。
• 调参建议 ：论文隐含λ≈0.3−0.5\lambda \approx 0.3-0.5λ≈0.3−0.5（中等），实验中稳定收敛，避免PPO的偏差-方差问题（λ\lambdaλ在GAE中）。

5. 与RL训练的整合：训练循环中的作用

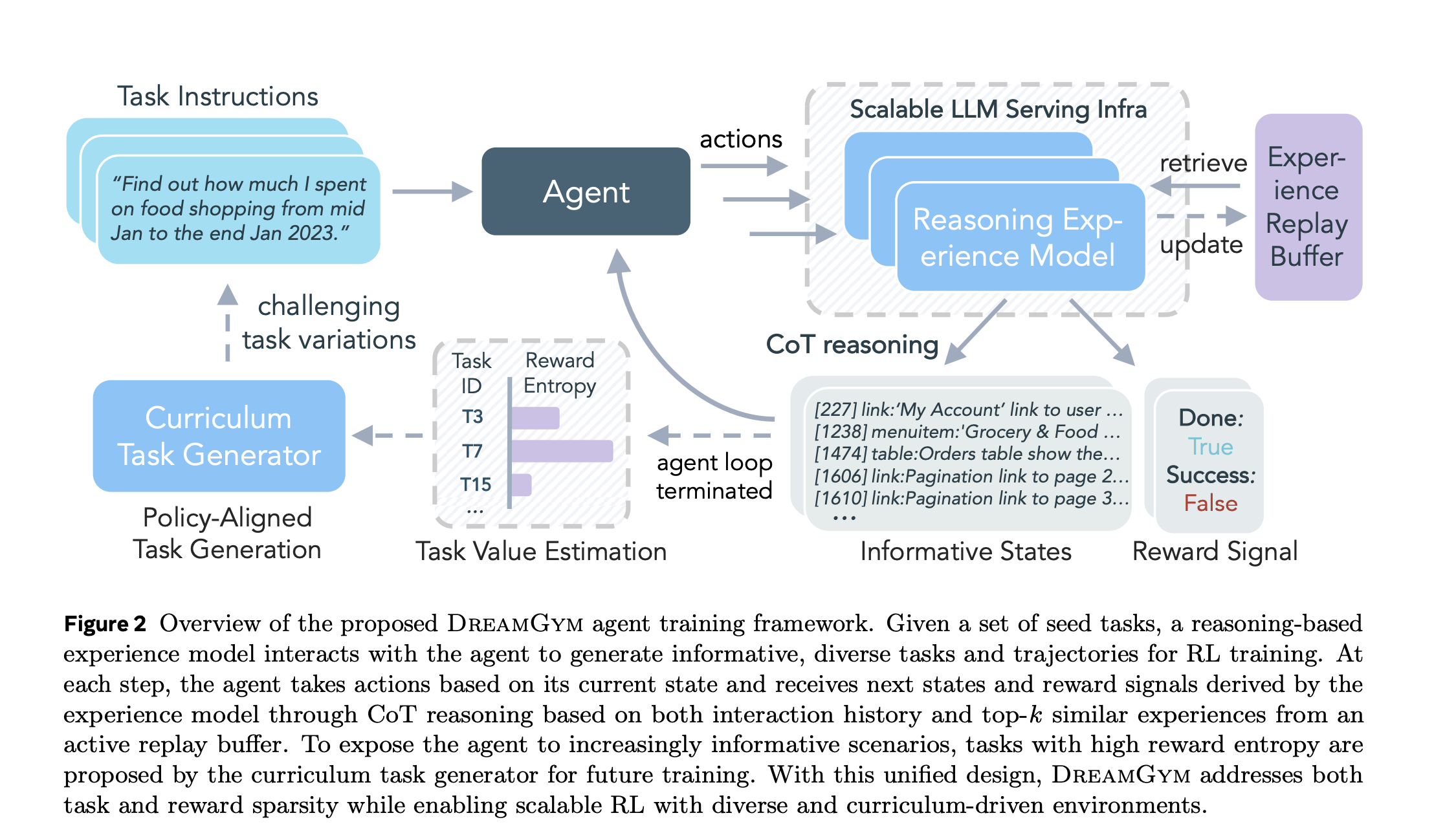
如图2和4.3节所述，课程生成嵌入合成环境训练循环：

1. 初始化 ：种子任务集{τ0}\{\tau_0\}{τ0}。
2. 交互 ：代理πθ\pi_\thetaπθ选at∈Aa_t \in Aat∈A，MexpM_{\text{exp}}Mexp生成(st+1,rt+1)(s_{t+1}, r_{t+1})(st+1,rt+1)（用CoT，公式4）。
3. RL更新 ：轨迹ϵ={τ0∣s0,a0,... }\epsilon = \{\tau_0 | s_0, a_0, \dots\}ϵ={τ0∣s0,a0,...}喂PPO/GRPO，优化θ\thetaθ（公式1-3）。
4. 课程扩展 ：计算VτV_\tauVτ选高熵种子 → MtaskM_{\text{task}}Mtask生成变体τt\tau_tτt → 更新任务集。
5. 循环 ：至收敛或预算尽。附录B.1证明：在信任域（trust-region）假设下，合成经验的策略改进下界E[∇J]≥ϵ>0\mathbb{E}[\nabla J] \geq \epsilon > 0E[∇J]≥ϵ>0。

与PPO/GRPO协同：

• PPO：VτV_\tauVτ辅助GAE的A^tPPO\hat{A}^{\text{PPO}}tA^tPPO，高熵任务丰富V(st+l+1)V(s{t+l+1})V(st+l+1)估计。
• GRPO：直接用GGG的rˉ,σr\bar{r}, \sigma_rrˉ,σr，VτV_\tauVτ量化组变异，提升相对归一化。

实验证据：在WebArena（非RL-ready），课程生成让DreamGym+30% vs. SOTA；在RL-ready环境，匹配GRPO/PPO，但零真实交互。

6. 启发与局限

潜力 ：这不是静态课程（如Teacher-Student），而是代理对齐的动态生成 （policy-aligned），适用于任意域（web、工具使用）。对开发者：从少量种子起步，λ\lambdaλ调稳定性。
局限 ：依赖MtaskM_{\text{task}}Mtask质量（LLM幻觉可能生畸形τt\tau_tτt）；nnn采样需平衡计算（小nnn方差不准）。未来可加人类反馈（RLHF）精炼种子。

总之，课程任务生成让DreamGym从"数据饥饿"转向"自适应供给"，是RL scalability的关键。（参考arXiv:2511.03773v2，2025.11.10）

DreamGym: 整体训练框架伪代码

基于论文《Scaling Agent Learning via Experience Synthesis》（arXiv:2511.03773v2）的描述，我为你提供一个简化的伪代码实现，聚焦于DreamGym的核心组件：推理经验模型（Reasoning Experience Model, Mexp⁡M_{\exp}Mexp）、经验重放缓冲区（Experience Replay Buffer）、课程任务生成器（Curriculum Task Generator）和合成环境下的RL训练循环（使用PPO或GRPO作为示例）。伪代码采用Python-like风格，便于理解和扩展。

伪代码覆盖了论文4.3节的"合成环境策略训练"流程：从种子任务开始，交替生成rollout、RL更新和任务扩展。假设：

• 代理策略πθ\pi_\thetaπθ（e.g., LLM-based policy）。
• Mexp⁡M_{\exp}Mexp已通过SFT训练好（公式5）。
• 奖励为二元结局奖励（r∈{0,1}r \in \{0,1\}r∈{0,1}）。
• 超参数：kkk（检索top-k）、nnn（熵采样次数）、λ\lambdaλ（合成任务比例）、mmm（种子任务数）、γ,λGAE\gamma, \lambda_{\text{GAE}}γ,λGAE（RL相关）。

1. 辅助函数：经验模型推理（公式4）

def experience_model_step(s_t, a_t, history, tau, replay_buffer, k):
    # 检索top-k相似轨迹
    D_k = replay_buffer.retrieve_top_k(s_t, a_t, k)  # 基于cos(φ(s_t, a_t), φ(s_i, a_i))
    
    # CoT推理生成R_t
    R_t = M_exp.generate_reasoning(history + [ (s_t, a_t) ], D_k, tau)
    
    # 预测下一状态和奖励
    s_{t+1}, r_{t+1} = M_exp.predict_next(R_t, s_t, a_t, history, D_k, tau)
    
    # 更新缓冲区（在线丰富）
    replay_buffer.update( (s_t, a_t, s_{t+1}, r_{t+1}, R_t) )
    
    return s_{t+1}, r_{t+1}

2. 辅助函数：任务价值估计（奖励熵，公式7）

def estimate_task_value(tau, pi_theta, n, M_exp, replay_buffer):
    # 在组G中采样n次rollout（合成环境）
    rewards = []
    for _ in range(n):
        rollout = generate_rollout(tau, pi_theta, M_exp, replay_buffer)  # 多轮交互
        r_final = rollout.rewards[-1]  # 结局奖励
        rewards.append(r_final)
    
    mean_r = sum(rewards) / n
    variance = sum( (r - mean_r)**2 for r in rewards ) / n  # V_τ
    
    return variance  # 高熵表示挑战性任务

3. 辅助函数：生成rollout（多轮交互）

def generate_rollout(tau, pi_theta, M_exp, replay_buffer, max_steps=100):
    s_0 = initialize_state(tau)  # 初始抽象状态
    history = []
    trajectory = {'states': [s_0], 'actions': [], 'rewards': []}
    
    for t in range(max_steps):
        a_t = pi_theta.sample_action(trajectory['states'][-1], tau)  # π_θ(s_t) ~ Δ(A)
        history.append( (trajectory['states'][-1], a_t) )
        
        s_{t+1}, r_{t+1} = experience_model_step(trajectory['states'][-1], a_t, history, tau, replay_buffer, k)
        
        trajectory['states'].append(s_{t+1})
        trajectory['actions'].append(a_t)
        trajectory['rewards'].append(r_{t+1})
        
        if is_terminal(s_{t+1}):  # done=True
            break
    
    return trajectory  # ε = {τ | s0, a0, ...}

4. 辅助函数：课程任务生成（公式6）

def generate_curriculum_tasks(seeds, M_task, lambda_param):
    # 过滤高价值种子（基于V_τ阈值）
    high_value_seeds = [tau for tau in seeds if estimate_task_value(tau, pi_theta, n, M_exp, replay_buffer) > threshold]
    
    # 生成m个变体
    new_tasks = []
    for _ in range(m):
        tau_t = M_task.generate_variations(high_value_seeds)  # τ_t = M_task({τ_i^{t-1}})
        new_tasks.append(tau_t)
    
    # 混合：λ比例新任务，(1-λ)原任务
    task_set = (1 - lambda_param) * seeds + lambda_param * new_tasks
    
    return task_set

5. 整体训练循环（合成环境RL，论文4.3）

def dreamgym_train(seed_tasks, num_iterations, rl_algo='PPO'):
    # 初始化
    replay_buffer = ExperienceReplayBuffer(initialize_with_offline_data())  # 离线种子
    M_exp = load_trained_exp_model()  # SFT后
    M_task = M_exp  # 参数共享
    pi_theta = initialize_policy()  # e.g., LLM代理
    V_func = initialize_value_function() if rl_algo == 'PPO' else None  # PPO需V
    
    task_set = seed_tasks  # 初始任务集
    
    for iter in range(num_iterations):
        trajectories = []  # 本迭代rollout集
        
        # 步骤1: 生成多样rollout
        for tau in task_set:
            traj = generate_rollout(tau, pi_theta, M_exp, replay_buffer, max_steps)
            trajectories.append(traj)
        
        # 步骤2: RL更新策略（PPO或GRPO，公式1-3）
        if rl_algo == 'PPO':
            advantages = compute_gae(trajectories, V_func, gamma, lambda_gae)  # 公式2: Â^PPO_t
            update_policy_ppo(pi_theta, trajectories, advantages)  # ∇J(θ) = E[∇log π · Â]
        elif rl_algo == 'GRPO':
            groups = group_trajectories_by_task(trajectories)  # 按τ分组G
            advantages = compute_grpo(groups)  # 公式3: Â^GRPO_t = (r - mean_G)/std_G
            update_policy_grpo(pi_theta, trajectories, advantages)
        
        # 步骤3: 课程扩展任务集
        task_set = generate_curriculum_tasks(task_set, M_task, lambda_param)
        
        # 可选：评估（e.g., sim-to-real转移）
        if iter % eval_freq == 0:
            eval_policy(pi_theta, real_env)  # 少量真实finetune
    
    return pi_theta  # 训练后策略

解释与扩展笔记

• 关键循环 ：交替"生成（合成rollout）→ 更新（RL）→ 扩展（课程）"，确保数据与πθ\pi_\thetaπθ共进化。附录B.1的理论下界保证了合成经验的有效性（trust-region下E[∇J]≥ϵ\mathbb{E}[\nabla J] \geq \epsilonE[∇J]≥ϵ）。
• 效率：全合成，无真实交互；缓冲区从离线（如WebArena）初始化，在线更新。
• PPO vs. GRPO ：伪代码中分支处理；GRPO更适合组高熵任务（VτV_\tauVτ）。
• 实现提示 ：用HuggingFace Transformers实现Mexp⁡M_{\exp}Mexp（CoT提示）；RL用Stable-Baselines3或自定义。完整代码需处理抽象状态SSS（文本精炼）。
• 局限 ：伪代码简化了检索ϕ(⋅)\phi(\cdot)ϕ(⋅)（用SentenceTransformer）和终端判断；实际调参k=5,n=20,λ=0.4k=5, n=20, \lambda=0.4k=5,n=20,λ=0.4。

这个伪代码捕捉了DreamGym的本质：统一、可扩展的RL基础设施。

后记

2025年12月3日于上海，在grok 4.1 thinking 辅助下完成。