深度学习——03 神经网络（3）-网络优化方法

3 网络优化方法

3.1 梯度下降算法回顾

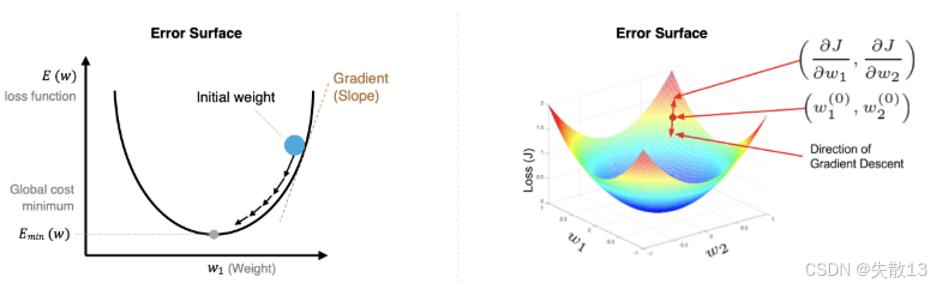
• 梯度下降是一种优化算法 ，目的是最小化损失函数（比如之前的 MSE、MAE）；

• 梯度方向是"损失函数增长最快的方向"。因此，参数更新要沿着梯度的反方向（减去梯度×学习率），才能让损失减小；

  • 左图（一维损失曲面）：参数从"初始点"出发，沿着梯度反方向逐步更新，最终到达"损失最小值点"；
  • 右图（二维损失曲面）：梯度是"当前点的斜率"，参数更新方向是梯度的反方向，逐步逼近全局最优；

  

• 公式：
  Wijnew=Wijold−η∂E∂Wij W_{ij}^{\text{new}} = W_{ij}^{\text{old}} - \eta \frac{\partial E}{\partial W_{ij}} Wijnew=Wijold−η∂Wij∂E

  • WijW_{ij}Wij：模型的参数（比如神经网络的权重）；

  • η\etaη：学习率（控制参数更新的"步长"）；

    • 学习率太小：参数更新慢，训练时间长（比如每次只走一小步，需要很多步才能到"山底"）；
    • 学习率太大：可能"跳过"最优解（比如大步跨过山谷，永远到不了最低点）；

  • ∂E∂Wij\frac{\partial E}{\partial W_{ij}}∂Wij∂E：损失函数对参数的梯度（决定参数更新的方向和大小）。

3.2 训练流程的几个概念

• 3 个核心概念

  • Epoch（轮次） ：用全部训练数据完整训练一次模型；

  • Batch Size（批次大小） ：每次参数更新时，用多少个样本计算梯度；

  • Iteration（迭代） ：用1 个 Batch 的数据更新一次参数；

• 例：假设数据集有 50000 个训练样本，现在选择 Batch Size = 256 对模型进行训练

  • 每个 Epoch 的样本数：50000（用完整数据训练一次）

  • 每个 Epoch 的 Batch 数 ：
    Batch 数=50000256≈195.31→向上取整为 196（因为剩下的样本也要训练） \text{Batch 数} = \frac{50000}{256} \approx 195.31 \rightarrow \text{向上取整为 196（因为剩下的样本也要训练）} Batch 数=25650000≈195.31→向上取整为 196（因为剩下的样本也要训练）

  • 每个 Epoch 的 Iteration 数：196（每个 Batch 对应 1 次参数更新）

  • 10 个 Epoch 的 Iteration 数 ：196×10=1960196 \times 10 = 1960196×10=1960

3.3 梯度下降的 3 种实现方式

• 核心区别：Batch Size 不同

  梯度下降方式	Batch Size	特点
  BGD	N （全部样本）	稳定，但计算量大（每次用全部数据算梯度），适合小数据集
  SGD	1 （单个样本）	计算快，但更新波动大（单个样本的梯度噪声大），适合想快速迭代的场景
  Mini-Batch	B （小批量，比如 32、64、256）	平衡了"稳定"和"速度" → 最常用（比如深度学习训练默认用这种）

• Batch 数计算：

  • 如果NNN能被BBB整除 → Batch 数 =N/BN/BN/B
  • 如果不能整除 → Batch 数 =N/B+1N/B + 1N/B+1（剩下的样本单独作为 1 个 Batch）

3.4 前向传播与反向传播

3.4.1 概述

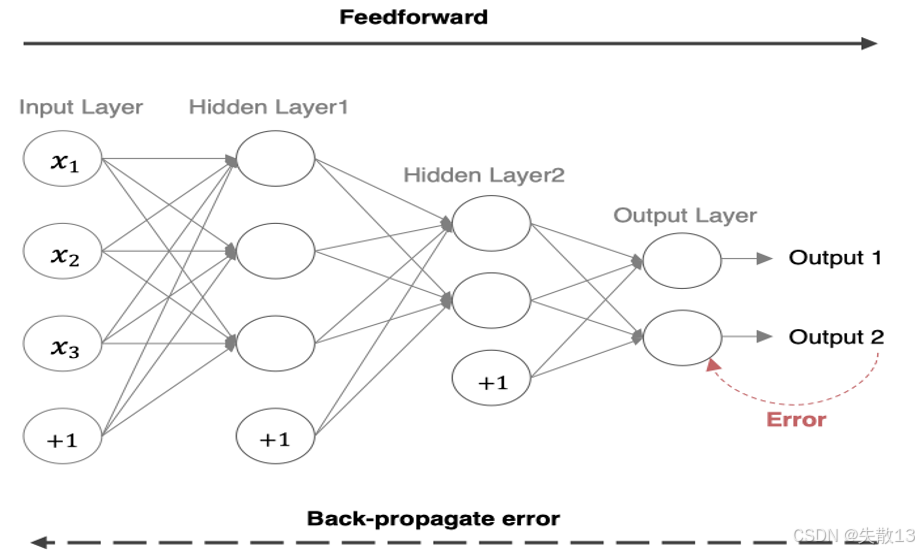
• 前向传播（Feedforward）：指的是数据输入的神经网络中，逐层向前传输，一直到运算到输出层为止；

  • 数据从**输入层（Input Layer）**开始，像x1、x2、x3x_1、x_2、x_3x1、x2、x3这类输入数据，带着"+1"偏置项（辅助调整输出），逐层传给 隐藏层（Hidden Layer1、Hidden Layer2） ，最后到 输出层（Output Layer） 算出结果（Output 1、Output 2）；
  • 简单说：输入数据"从前往后"流，算出预测结果 ，比如识别图片、预测数值，这一步是"算结果"的过程；

• 反向传播 （Back Propagation，即BP算法）：输出结果和"真实答案"对比会产生误差（Error），反向传播就是让误差"从后往前"走；

  • 用损失函数（比如均方误差）衡量误差大小，结合梯度下降算法 ，从输出层往回算，求每个连接参数（权重、偏置）对误差的影响（偏导数）；
  • 根据这些影响，更新参数（调整权重、偏置），让下次前向传播的结果更接近真实答案；
  • 简单说：误差"从后往前"传，指导参数更新 ，是神经网络"学习优化"的核心逻辑；

  

3.4.2 准备案例的网络结构

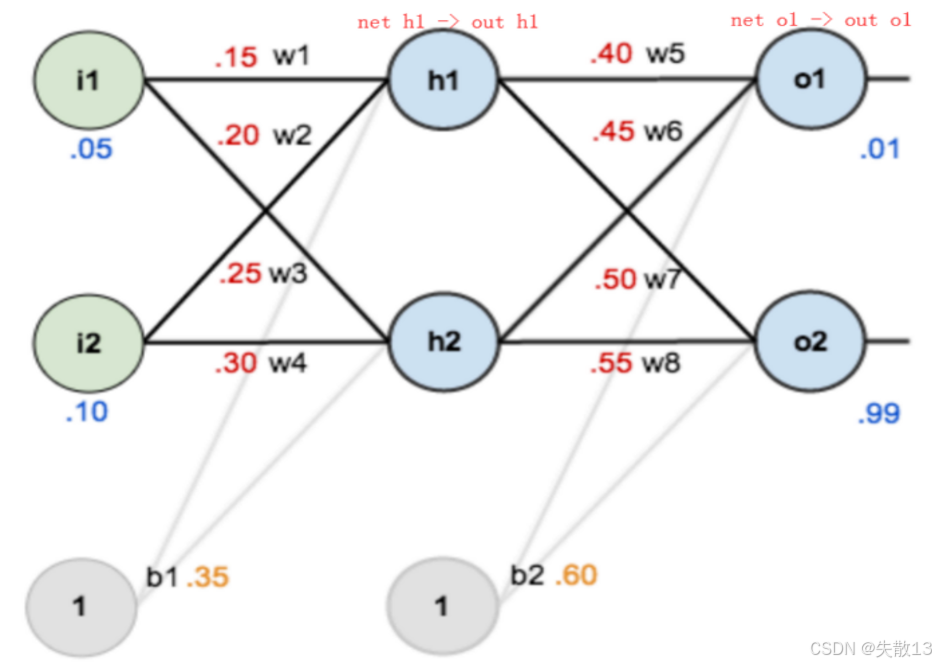
• 网络结构

  

  • 输入层 ：i1=0.05、i2=0.10（含偏置 b1=0.35、b2=0.60）

  • 隐藏层 ：2 个神经元 h1、h2（激活函数：Sigmoid）

  • 输出层 ：2 个神经元 o1、o2（激活函数：Sigmoid）

  • 权重 ：w1=0.15、w2=0.20、w3=0.25、w4=0.30、w5=0.40、w6=0.45、w7=0.50、w8=0.55

  • 真实标签 ：target_o1=0.01、target_o2=0.99

• 核心流程

  • 前向传播：输入 → 隐藏层 → 输出层，计算预测值与损失

  • 反向传播：从输出层 → 隐藏层 → 输入层，反向计算梯度并更新权重

3.4.3 前向传播（计算预测值与损失）

• 隐藏层（h1、h2h1、h2h1、h2）的计算：输入nethnet_hneth，经过 Sigmoid 激活函数（out=11+e−net\text{out} = \frac{1}{1 + e^{-\text{net}}}out=1+e−net1）后输出
  h1的输入：neth1=w1⋅i1+w2⋅i2+b1⋅1=0.15⋅0.05+0.20⋅0.10+0.35⋅1=0.0075+0.02+0.35=0.3775h1的输出：outh1=11+e−neth1=11+e−0.3775≈0.5933h2的输入：neth2=w3⋅i1+w4⋅i2+b1⋅1=0.25⋅0.05+0.30⋅0.10+0.35⋅1=0.0125+0.03+0.35=0.3925h2的输出：outh2=11+e−neth2=11+e−0.3925≈0.5969 h1的输入：\text{net}{h1} = w1 \cdot i1 + w2 \cdot i2 + b1 \cdot 1 = 0.15 \cdot 0.05 + 0.20 \cdot 0.10 + 0.35 \cdot 1 = 0.0075 + 0.02 + 0.35 = 0.3775 \\ h1的输出：\text{out}{h1} = \frac{1}{1 + e^{-\text{net}{h1}}} = \frac{1}{1 + e^{-0.3775}} \approx 0.5933 \\ h2的输入：\text{net}{h2} = w3 \cdot i1 + w4 \cdot i2 + b1 \cdot 1 = 0.25 \cdot 0.05 + 0.30 \cdot 0.10 + 0.35 \cdot 1 = 0.0125 + 0.03 + 0.35 = 0.3925 \\ h2的输出：\text{out}{h2} = \frac{1}{1 + e^{-\text{net}{h2}}} = \frac{1}{1 + e^{-0.3925}} \approx 0.5969 h1的输入：neth1=w1⋅i1+w2⋅i2+b1⋅1=0.15⋅0.05+0.20⋅0.10+0.35⋅1=0.0075+0.02+0.35=0.3775h1的输出：outh1=1+e−neth11=1+e−0.37751≈0.5933h2的输入：neth2=w3⋅i1+w4⋅i2+b1⋅1=0.25⋅0.05+0.30⋅0.10+0.35⋅1=0.0125+0.03+0.35=0.3925h2的输出：outh2=1+e−neth21=1+e−0.39251≈0.5969

• 输出层（o1、o2o1、o2o1、o2） 的计算：输入nethnet_hneth，经过 Sigmoid 激活函数（out=11+e−net\text{out} = \frac{1}{1 + e^{-\text{net}}}out=1+e−net1）后输出
  o1的输入：neto1=w5⋅outh1+w6⋅outh2+b2⋅1=0.40⋅0.5933+0.45⋅0.5969+0.60⋅1≈0.2373+0.2686+0.60=1.1059o1的输出：outo1=11+e−neto1=11+e−1.1059≈0.7514o2的输入：neto2=w7⋅outh1+w8⋅outh2+b2⋅1=0.50⋅0.5933+0.55⋅0.5969+0.60⋅1≈0.2966+0.3283+0.60=1.2249o2的输出：outo2=11+e−neto2=11+e−1.2249≈0.7729 o1的输入：\text{net}{o1} = w5 \cdot \text{out}{h1} + w6 \cdot \text{out}{h2} + b2 \cdot 1 = 0.40 \cdot 0.5933 + 0.45 \cdot 0.5969 + 0.60 \cdot 1 \approx 0.2373 + 0.2686 + 0.60 = 1.1059 \\ o1的输出：\text{out}{o1} = \frac{1}{1 + e^{-\text{net}{o1}}} = \frac{1}{1 + e^{-1.1059}} \approx 0.7514 \\ o2的输入：\text{net}{o2} = w7 \cdot \text{out}{h1} + w8 \cdot \text{out}{h2} + b2 \cdot 1 = 0.50 \cdot 0.5933 + 0.55 \cdot 0.5969 + 0.60 \cdot 1 \approx 0.2966 + 0.3283 + 0.60 = 1.2249 \\ o2的输出：\text{out}{o2} = \frac{1}{1 + e^{-\text{net}{o2}}} = \frac{1}{1 + e^{-1.2249}} \approx 0.7729 o1的输入：neto1=w5⋅outh1+w6⋅outh2+b2⋅1=0.40⋅0.5933+0.45⋅0.5969+0.60⋅1≈0.2373+0.2686+0.60=1.1059o1的输出：outo1=1+e−neto11=1+e−1.10591≈0.7514o2的输入：neto2=w7⋅outh1+w8⋅outh2+b2⋅1=0.50⋅0.5933+0.55⋅0.5969+0.60⋅1≈0.2966+0.3283+0.60=1.2249o2的输出：outo2=1+e−neto21=1+e−1.22491≈0.7729

• 均方误差（MSE）损失：
  Etotal=12∑(target−out)2=12[(0.01−0.7514)2+(0.99−0.7729)2]≈12[0.5490+0.0471]=0.2981 E_{\text{total}} = \frac{1}{2} \sum (\text{target} - \text{out})^2 = \frac{1}{2} \left[ (0.01 - 0.7514)^2 + (0.99 - 0.7729)^2 \right] \approx \frac{1}{2} \left[ 0.5490 + 0.0471 \right] = 0.2981 Etotal=21∑(target−out)2=21[(0.01−0.7514)2+(0.99−0.7729)2]≈21[0.5490+0.0471]=0.2981

3.4.4 反向传播（计算梯度并更新权重）

• 反向传播的核心是链式法则 ：梯度从输出层反向传递，逐层计算损失对权重的偏导，再用梯度下降更新权重。

3.4.4.1 输出层 → 隐藏层（以 w5 为例）

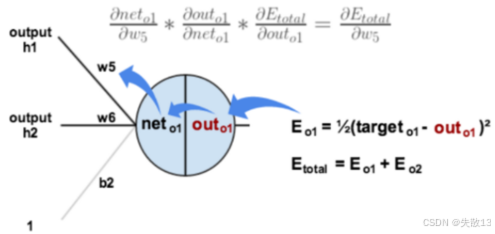
• 目标：计算∂Etotal∂w5\frac{\partial E_{\text{total}}}{\partial w5}∂w5∂Etotal，即误差EEE对w5w5w5的导数。需要先求误差EEE对outo1out_{o1}outo1的导数，再求outo1out_{o1}outo1对neto1net_{o1}neto1的导数，最后再求neto1net_{o1}neto1对w5w5w5的导数，通过链式法则拆解为下式
  ∂Etotal∂w5=∂Etotal∂outo1⋅∂outo1∂neto1⋅∂neto1∂w5 \frac{\partial E_{\text{total}}}{\partial w5} = \frac{\partial E_{\text{total}}}{\partial \text{out}{o1}} \cdot \frac{\partial \text{out}{o1}}{\partial \text{net}{o1}} \cdot \frac{\partial \text{net}{o1}}{\partial w5} ∂w5∂Etotal=∂outo1∂Etotal⋅∂neto1∂outo1⋅∂w5∂neto1
  

• 计算∂Etotal∂outo1\frac{\partial E_{\text{total}}}{\partial \text{out}{o1}}∂outo1∂Etotal
  Etotal=12(targeto1−outo1)2+12(targeto2−outo2)2∂Etotal∂outo1=2∗12(targeto1−outo1)2−1∗(−1)+0=−(targeto1−outo1)=−(0.01−0.7514)=0.7414 E{total} = \frac{1}{2}(target_{o1} - out_{o1})^2 + \frac{1}{2}(target_{o2} - out_{o2})^2 \\ \frac{\partial E_{total}}{\partial out_{o1}} = 2 * \frac{1}{2}(target_{o1} - out_{o1})^{2 - 1} * (-1) + 0 = -(target_{o1} - out_{o1}) = -(0.01 - 0.7514) = 0.7414 Etotal=21(targeto1−outo1)2+21(targeto2−outo2)2∂outo1∂Etotal=2∗21(targeto1−outo1)2−1∗(−1)+0=−(targeto1−outo1)=−(0.01−0.7514)=0.7414

• 计算∂outo1∂neto1\frac{\partial \text{out}{o1}}{\partial \text{net}{o1}}∂neto1∂outo1（Sigmoid 导数）

  • 只要outo1\text{out}{o1}outo1是 Sigmoid 激活的输出，∂outo1∂neto1\boldsymbol{\frac{\partial \text{out}{o1}}{\partial \text{net}_{o1}}}∂neto1∂outo1就等价于 Sigmoid 函数的导数

  Sigmoid导数：∂out∂net=out⋅(1−out)outo1=11+e−neto1∂outo1∂neto1=outo1⋅(1−outo1)=0.7514⋅(1−0.7514)≈0.1868 Sigmoid 导数： \frac{\partial \text{out}}{\partial \text{net}} = \text{out} \cdot (1 - \text{out}) \\ out_{o1} = \frac{1}{1 + e^{-net_{o1}}} \\ \frac{\partial \text{out}{o1}}{\partial \text{net}{o1}} = \text{out}{o1} \cdot (1 - \text{out}{o1}) = 0.7514 \cdot (1 - 0.7514) \approx 0.1868 Sigmoid导数：∂net∂out=out⋅(1−out)outo1=1+e−neto11∂neto1∂outo1=outo1⋅(1−outo1)=0.7514⋅(1−0.7514)≈0.1868

• 计算∂neto1∂w5\frac{\partial \text{net}{o1}}{\partial w5}∂w5∂neto1
  neto1=w5∗outh1+w6∗outh2+b2∗1∂neto1∂w5=outh1=0.5933 net{o1} = w_5 * out_{h1} + w_6 * out_{h2} + b_2 * 1 \\ \frac{\partial \text{net}{o1}}{\partial w5} = \text{out}{h1} = 0.5933 neto1=w5∗outh1+w6∗outh2+b2∗1∂w5∂neto1=outh1=0.5933

• 合并链式法则
  ∂Etotal∂w5=0.7414⋅0.1868⋅0.5933≈0.0822 \frac{\partial E_{\text{total}}}{\partial w5} = 0.7414 \cdot 0.1868 \cdot 0.5933 \approx 0.0822 ∂w5∂Etotal=0.7414⋅0.1868⋅0.5933≈0.0822

• 使用梯度下降算法（公式见3.1 梯度下降算法回顾）更新 w5（学习率η=0.5\eta = 0.5η=0.5）
  w5new=w5old−η⋅∂Etotal∂w5=0.40−0.5⋅0.0822≈0.3589 w5^{\text{new}} = w5^{\text{old}} - \eta \cdot \frac{\partial E_{\text{total}}}{\partial w5} = 0.40 - 0.5 \cdot 0.0822 \approx 0.3589 w5new=w5old−η⋅∂w5∂Etotal=0.40−0.5⋅0.0822≈0.3589

• 同理可以得出w6new、w7new、w8neww6^{\text{new}}、w7^{\text{new}}、w8^{\text{new}}w6new、w7new、w8new。

3.4.4.2 隐藏层 → 输入层（以 w1 为例）

• 目标：计算损失EtotalE_{\text{total}}Etotal对输入层到隐藏层权重w1w1w1的偏导数 ，即∂Etotal∂w1\boldsymbol{\frac{\partial E_{\text{total}}}{\partial w1}}∂w1∂Etotal；

  • w1w1w1是输入层i1i1i1到隐藏层h1h1h1的连接权重 （w1=0.15，连接 i1 → h1）；
  • 要更新w1w1w1，需用链式法则 ，把误差从输出层反向传递到w1w1w1，拆解成多步偏导的乘积；

• 根据链式法则，误差对w1w1w1的偏导可拆为4层传递关系 （从损失到输出层→隐藏层→隐藏层输入→权重w1w1w1）：
  ∂Etotal∂w1=∂Etotal∂outh1⋅∂outh1∂neth1⋅∂neth1∂w1 \frac{\partial E_{\text{total}}}{\partial w1} = \frac{\partial E_{\text{total}}}{\partial \text{out}{h1}} \cdot \frac{\partial \text{out}{h1}}{\partial \text{net}{h1}} \cdot \frac{\partial \text{net}{h1}}{\partial w1} ∂w1∂Etotal=∂outh1∂Etotal⋅∂neth1∂outh1⋅∂w1∂neth1

• 但因为隐藏层h1h1h1的输出outh1\text{out}_{h1}outh1会影响两个输出层神经元o1o1o1、o2o2o2 ，所以还要进一步拆分：
  

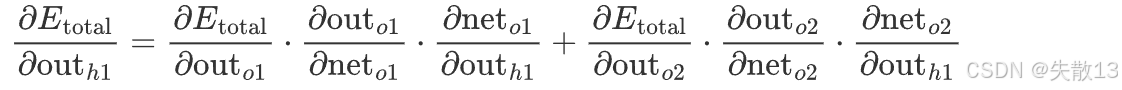
• 所以：
  

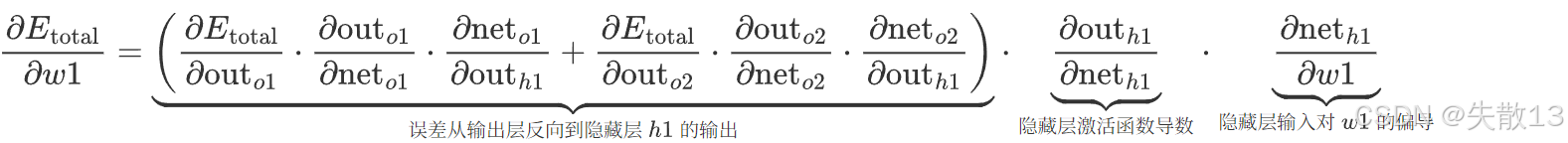
• 计算∂Etotal∂outo1\frac{\partial E_{\text{total}}}{\partial \text{out}{o1}}∂outo1∂Etotal与∂Etotal∂outo2\frac{\partial E{\text{total}}}{\partial \text{out}{o2}}∂outo2∂Etotal
  ∂Etotal∂outo1=−(targeto1−outo1)=−(0.01−0.7514)=0.7414∂Etotal∂outo2=−(targeto2−outo2)=−(0.99−0.7729)=−0.2171 \frac{\partial E{\text{total}}}{\partial \text{out}{o1}} = -(\text{target}{o1} - \text{out}{o1}) = -(0.01 - 0.7514) = 0.7414 \\ \frac{\partial E{\text{total}}}{\partial \text{out}{o2}} = -(\text{target}{o2} - \text{out}_{o2}) = -(0.99 - 0.7729) = -0.2171 ∂outo1∂Etotal=−(targeto1−outo1)=−(0.01−0.7514)=0.7414∂outo2∂Etotal=−(targeto2−outo2)=−(0.99−0.7729)=−0.2171

• 计算∂outo1∂neto1\boldsymbol{\frac{\partial \text{out}{o1}}{\partial \text{net}{o1}}}∂neto1∂outo1与∂outo2∂neto2\frac{\partial \text{out}{o2}}{\partial \text{net}{o2}}∂neto2∂outo2（Sigmoid 导数）
  ∂outo1∂neto1=outo1⋅(1−outo1)=0.7514⋅(1−0.7514)≈0.1868∂outo2∂neto2=outo2⋅(1−outo2)=0.7729⋅(1−0.7729)≈0.1761 \frac{\partial \text{out}{o1}}{\partial \text{net}{o1}} = \text{out}{o1} \cdot (1 - \text{out}{o1}) = 0.7514 \cdot (1 - 0.7514) \approx 0.1868 \\ \frac{\partial \text{out}{o2}}{\partial \text{net}{o2}} = \text{out}{o2} \cdot (1 - \text{out}{o2}) = 0.7729 \cdot (1 - 0.7729) \approx 0.1761 ∂neto1∂outo1=outo1⋅(1−outo1)=0.7514⋅(1−0.7514)≈0.1868∂neto2∂outo2=outo2⋅(1−outo2)=0.7729⋅(1−0.7729)≈0.1761

• 计算∂neto1∂outh1\frac{\partial \text{net}{o1}}{\partial \text{out}{h1}}∂outh1∂neto1和∂neto2∂outh1\frac{\partial \text{net}{o2}}{\partial \text{out}{h1}}∂outh1∂neto2（输出层输入neto1\text{net}{o1}neto1、neto2\text{net}{o2}neto2对隐藏层输出outh1\text{out}{h1}outh1的偏导（即权重w5w5w5、w7w7w7））
  neto1=w5⋅outh1+w6⋅outh2+b2，所以：∂neto1∂outh1=w5=0.40neto2=w7⋅outh1+w8⋅outh2+b2，所以：∂neto2∂outh1=w7=0.50 \text{net}{o1} = w5 \cdot \text{out}{h1} + w6 \cdot \text{out}{h2} + b2，所以： \frac{\partial \text{net}{o1}}{\partial \text{out}{h1}} = w5 = 0.40 \\ \text{net}{o2} = w7 \cdot \text{out}{h1} + w8 \cdot \text{out}{h2} + b2，所以： \frac{\partial \text{net}{o2}}{\partial \text{out}_{h1}} = w7 = 0.50 neto1=w5⋅outh1+w6⋅outh2+b2，所以：∂outh1∂neto1=w5=0.40neto2=w7⋅outh1+w8⋅outh2+b2，所以：∂outh1∂neto2=w7=0.50

• 计算∂outh1∂neth1\boldsymbol{\frac{\partial \text{out}{h1}}{\partial \text{net}{h1}}}∂neth1∂outh1（Sigmoid 导数）
  ∂outh1∂neth1=0.5933⋅(1−0.5933)≈0.2426 \frac{\partial \text{out}{h1}}{\partial \text{net}{h1}} = 0.5933 \cdot (1 - 0.5933) \approx 0.2426 ∂neth1∂outh1=0.5933⋅(1−0.5933)≈0.2426

• 计算∂neth1∂w1\boldsymbol{\frac{\partial \text{net}{h1}}{\partial w1}}∂w1∂neth1（ 隐藏层h1h1h1的输入neth1\text{net}{h1}neth1对权重w1w1w1的偏导（即输入i1i1i1的值 ））
  neth1=w1⋅i1+w2⋅i2+b1，所以：∂neth1∂w1=i1=0.05 \text{net}{h1} = w1 \cdot i1 + w2 \cdot i2 + b1，所以：\frac{\partial \text{net}{h1}}{\partial w1} = i1 = 0.05 neth1=w1⋅i1+w2⋅i2+b1，所以：∂w1∂neth1=i1=0.05

• 合并链式法则
  ∂Etotal∂w1=(0.7414⋅0.1868⋅0.40+(−0.2171)⋅0.1761⋅0.50)⋅0.2426⋅0.05=(0.0555−0.0191)⋅0.0121=0.0364⋅0.0121≈0.00044 \begin{align*} \frac{\partial E_{\text{total}}}{\partial w1} &= \left( 0.7414 \cdot 0.1868 \cdot 0.40 + (-0.2171) \cdot 0.1761 \cdot 0.50 \right) \cdot 0.2426 \cdot 0.05 \\ &= \left( 0.0555 - 0.0191 \right) \cdot 0.0121 \\ &= 0.0364 \cdot 0.0121 \\ &\approx 0.00044 \end{align*} ∂w1∂Etotal=(0.7414⋅0.1868⋅0.40+(−0.2171)⋅0.1761⋅0.50)⋅0.2426⋅0.05=(0.0555−0.0191)⋅0.0121=0.0364⋅0.0121≈0.00044

• 更新 w1
  w1new=w1old−η⋅∂Etotal∂w1=0.15−0.5⋅0.0004≈0.1498 w1^{\text{new}} = w1^{\text{old}} - \eta \cdot \frac{\partial E_{\text{total}}}{\partial w1} = 0.15 - 0.5 \cdot 0.0004 \approx 0.1498 w1new=w1old−η⋅∂w1∂Etotal=0.15−0.5⋅0.0004≈0.1498

3.4.5 代码

• 导包：

  import torch  
  from torch import nn  
  # 从 torch 中导入 optim 模块，用于定义优化器（如 SGD、Adam 等）
  from torch import optim  

• 定义神经网络类：

  # 定义神经网络类，继承 nn.Module（PyTorch 中自定义网络的标准写法）
  class Model(nn.Module):
      # 初始化方法，构建网络结构并设置参数初始值
      def __init__(self):
          # 调用父类（nn.Module）的初始化方法，必须执行，确保模块正确初始化
          super(Model, self).__init__()
          
          # 定义第一层线性层（对应隐藏层 1）：输入维度 2（i1、i2），输出维度 2（h1、h2 两个神经元）
          self.linear1 = nn.Linear(2, 2)
          # 定义第二层线性层（对应隐藏层 2/输出层前的线性变换）：输入维度 2（h1、h2 输出），输出维度 2（o1、o2 两个神经元）
          self.linear2 = nn.Linear(2, 2)
          
          # 手动初始化第一层线性层的权重：对应 w1=0.15, w2=0.20（第一行）；w3=0.25, w4=0.30（第二行）
          self.linear1.weight.data = torch.tensor([[0.15, 0.20], [0.25, 0.30]])
          # 手动初始化第二层线性层的权重：对应 w5=0.40, w6=0.45（第一行）；w7=0.50, w8=0.55（第二行）
          self.linear2.weight.data = torch.tensor([[0.40, 0.45], [0.50, 0.55]])
          # 手动初始化第一层线性层的偏置：b1=0.35（两个神经元共享偏置，这里实际是 h1、h2 的偏置，示例中写法可优化但符合题意）
          self.linear1.bias.data = torch.tensor([0.35, 0.35])  
          # 手动初始化第二层线性层的偏置：b2=0.60（两个神经元共享偏置，对应 o1、o2 的偏置）
          self.linear2.bias.data = torch.tensor([0.60, 0.60])
  
      # 前向传播方法：定义数据从输入到输出的计算流程
      def forward(self, x):
          # 第一步：数据经过第一层线性层（linear1），计算隐藏层 1 的净输入（net_h1）
          x = self.linear1(x)
          # 第二步：对 linear1 的输出应用 Sigmoid 激活函数，得到隐藏层 1 的输出（out_h1）
          x = torch.sigmoid(x)
          # 第三步：数据经过第二层线性层（linear2），计算输出层的净输入（net_o1、net_o2）
          x = self.linear2(x)
          # 第四步：对 linear2 的输出应用 Sigmoid 激活函数，得到最终输出（out_o1、out_o2）
          x = torch.sigmoid(x)
          # 返回输出结果，用于前向传播预测或损失计算
          return x

• 主程序入口：

  # 主程序入口：当脚本直接运行时执行以下逻辑
  if __name__ == '__main__':
      # 定义网络输入值：对应 i1=0.05，i2=0.10（批量维度为 1，即单个样本）
      inputs = torch.tensor([[0.05, 0.10]])
      # 定义目标值（真实标签）：对应 target_o1=0.01，target_o2=0.99（批量维度为 1）
      target = torch.tensor([[0.01, 0.99]])
      
      # 实例化神经网络对象，创建 Model 类的实例
      model = Model()
      # 执行前向传播：将 inputs 输入模型，得到预测输出
      output = model(inputs)
      # 打印预测输出结果
      print("output-->", output)
      
      # 计算均方误差（MSE）损失：(output - target)^2 求和后除以 2（与公式 E_total = 1/2 Σ(...) 对应）
      loss = torch.sum((output - target) ** 2) / 2
      # 打印损失值
      print("loss-->", loss)
      
      # 定义优化器：使用随机梯度下降（SGD），优化模型的所有可训练参数，学习率 lr=0.5
      optimizer = optim.SGD(model.parameters(), lr=0.5)
      # 梯度清零：PyTorch 中默认会累积梯度，反向传播前需手动清零，避免影响计算
      optimizer.zero_grad()
      # 反向传播：自动计算损失对所有可训练参数的梯度（基于链式法则）
      loss.backward()
      # 打印第一层线性层（linear1）权重的梯度：对应 w1、w2、w3、w4 的梯度
      print("w1,w2,w3,w4-->", model.linear1.weight.grad.data)
      # 打印第二层线性层（linear2）权重的梯度：对应 w5、w6、w7、w8 的梯度
      print("w5,w6,w7,w8-->", model.linear2.weight.grad.data)
      # 参数更新：根据计算的梯度，用 SGD 优化器更新模型参数（权重和偏置）
      optimizer.step()
      
      # 打印模型当前的状态字典（包含所有参数的当前值），查看更新后的权重、偏置
      print(model.state_dict())

• 输出：

  output--> tensor([[0.7514, 0.7729]], grad_fn=<SigmoidBackward0>)
  loss--> tensor(0.2984, grad_fn=<DivBackward0>)
  w1,w2,w3,w4--> tensor([[0.0004, 0.0009],
          [0.0005, 0.0010]])
  w5,w6,w7,w8--> tensor([[ 0.0822,  0.0827],
          [-0.0226, -0.0227]])
  OrderedDict({'linear1.weight': tensor([[0.1498, 0.1996],
          [0.2498, 0.2995]]), 'linear1.bias': tensor([0.3456, 0.3450]), 'linear2.weight': tensor([[0.3589, 0.4087],
          [0.5113, 0.5614]]), 'linear2.bias': tensor([0.5308, 0.6190])})

3.5 梯度下降的优化方法

3.5.1 概述

• 在梯度下降优化算法中，把"损失 Loss"想象成一座山，参数www是"下山路径"，梯度下降是"找最陡的路下山"。但实际下山时，会遇到这些麻烦：

  

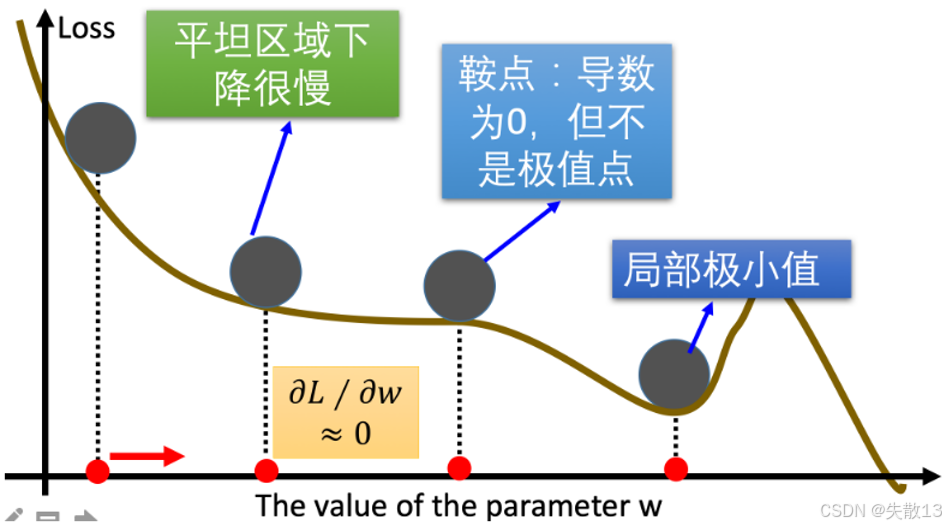
  • 平缓区域（梯度值小，优化变慢）

    • 现象 ：Loss 曲线很"平"，梯度∂L∂w≈0\frac{\partial L}{\partial w} \approx 0∂w∂L≈0（图中绿色区域）；

    • 问题：梯度是"下山方向"，梯度太小→每一步走得极慢，模型训练效率低；

  • 鞍点（梯度为 0，但不是最小值）

    • 现象 ：梯度∂L∂w=0\frac{\partial L}{\partial w} = 0∂w∂L=0，但这里不是"全局最低点"，而是"马鞍形状的中间点"（图中蓝色区域）；

    • 问题：梯度为 0 时，普通梯度下降会"认为到终点了"，但实际还没到全局最优，参数更新直接停住；

  • 局部最小值（参数不是最优）

    • 现象 ：走到一个"小坑"（局部最低点），梯度∂L∂w=0\frac{\partial L}{\partial w} = 0∂w∂L=0（图中深蓝色区域）；

    • 问题：梯度下降会停在这儿，但这不是"全局最小 Loss"，模型效果差；

• 为了让"下山"更顺畅，发明了优化算法（如 Momentum、AdaGrad、RMSprop、Adam 等），核心思路是：

  • 给梯度"加动力"：比如 Momentum 会保留之前的梯度方向，即便当前梯度小或为 0，也能靠"惯性"继续往前冲，跳过平缓区、鞍点；

  • 自适应调整学习率：比如 AdaGrad、Adam 会根据梯度历史动态调整每一步的"步长"，在平缓区大步走，在陡峭区小步走，避免卡局部最优。

3.5.2 方法1：指数加权平均

3.5.2.1 概述

• 指数加权平均（Exponential Weighted Average） ，核心是给不同时刻的数据分配不同权重，近期数据权重更高，远期数据权重指数级衰减，让平均值更关注"近期趋势"。常见于优化梯度下降（如 Adam 优化器）、时间序列预测（如温度预测，假设预测明天气温，"昨天气温"比"一个月前气温"更重要）；

• 指数加权平均值StS_tSt的计算分两种情况：
  St={Y1,当 t=0β⋅St−1+(1−β)⋅Yt,当 t>0 S_t = \begin{cases} Y_1, & \text{当 } t = 0 \\ \beta \cdot S_{t-1} + (1 - \beta) \cdot Y_t, & \text{当 } t > 0 \end{cases} St={Y1,β⋅St−1+(1−β)⋅Yt,当 t=0当 t>0

  • StS_tSt：ttt时刻的指数加权平均值（输出结果）

  • YtY_tYt：ttt时刻的原始数据（输入值，比如某时刻的梯度、温度等）

  • β\betaβ：权重系数（取值0∼10 \sim 10∼1），控制"历史数据的影响力"：

    • β\betaβ越大（如 0.99），历史数据权重越高，平均值越平滑（关注长期趋势）；
    • β\betaβ越小（如 0.9），近期数据权重越高，平均值对变化更敏感（关注短期波动）。

3.5.2.2 代码

import torch
import matplotlib.pyplot as plt

# 定义总天数（数据量），作为全局常量
ELEMENT_NUMBER = 30

# 1. 实际平均温度：生成并绘制原始随机温度数据
def test01():
    # 固定随机数种子（确保每次运行生成的随机数相同，方便复现结果）
    torch.manual_seed(0)
    # 生成 30 天的随机温度：均值为0、标准差为1的正态分布，再乘以10放大波动
    temperature = torch.randn(size=[ELEMENT_NUMBER, 1]) * 10
    # 打印原始温度数据（可选，用于调试或观察数值）
    print(temperature)
    
    # 生成 x 轴坐标：1~30 天（与温度数据一一对应）
    days = torch.arange(1, ELEMENT_NUMBER + 1, 1)
    # 绘制温度变化曲线（红色折线）
    plt.plot(days, temperature, color='r')
    # 绘制温度散点（红色点，突出原始数据）
    plt.scatter(days, temperature)
    # 显示图形（弹出窗口展示绘制结果）
    plt.show()
test01()

tensor([[-11.2584],
        [-11.5236],
        [ -2.5058],
        [ -4.3388],
        [  8.4871],
        [  6.9201],
        [ -3.1601],
        [-21.1522],
        [  3.2227],
        [-12.6333],
        [  3.4998],
        [  3.0813],
        [  1.1984],
        [ 12.3766],
        [ -1.4347],
        [ -1.1161],
        [ -6.1358],
        [  0.3159],
        [ -4.9268],
        [  2.4841],
        [  4.3970],
        [  1.1241],
        [ -8.4106],
        [-23.1604],
        [ -1.0231],
        [  7.9244],
        [ -2.8967],
        [  0.5251],
        [  5.2286],
        [ 23.0221]])

<Figure size 640x480 with 1 Axes>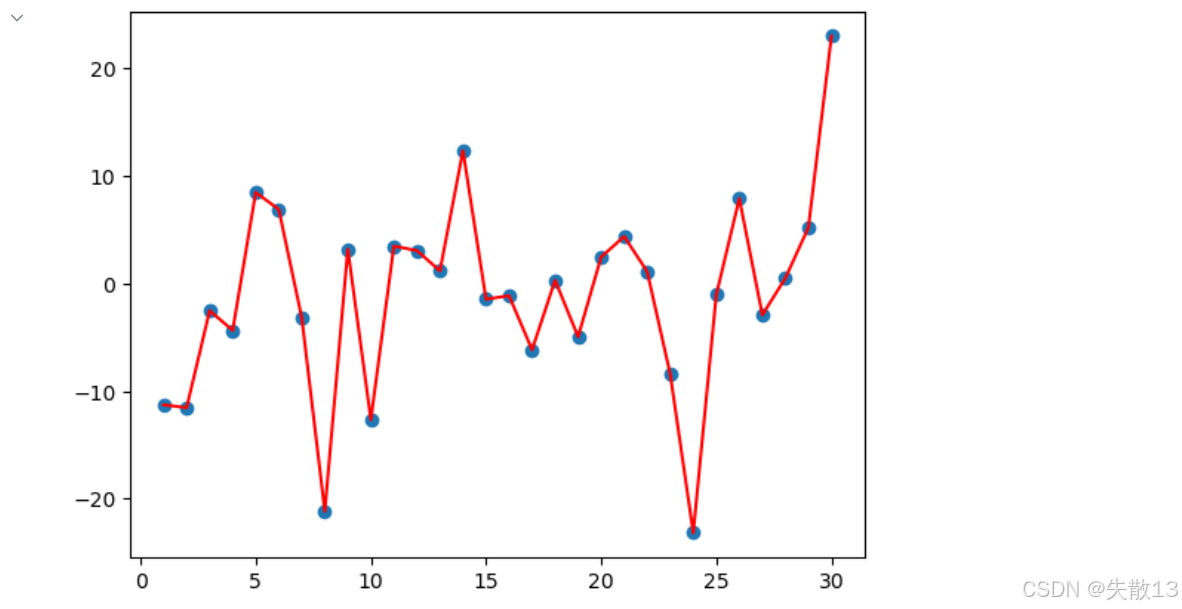

• 上图：原始温度的 "剧烈波动"
  • 蓝点 ：30 天的原始随机温度 （代码里 torch.randn 生成，模拟真实世界的随机波动）；
  • 红线：原始温度的折线连接，能更清晰看到 "每天温度的剧烈变化"------ 这是因为原始数据没经过任何平滑，完全保留了随机噪声；

# 2. 指数加权平均温度：用 EWA 算法平滑温度数据
def test02(beta=0.9):
    # 固定随机数种子（确保和 test01 生成的温度数据一致，方便对比）
    torch.manual_seed(0)
    # 生成和 test01 相同的 30 天随机温度
    temperature = torch.randn(size=[ELEMENT_NUMBER, 1]) * 10
    # 用于存储每天的指数加权平均结果
    exp_weight_avg = []
    
    # 遍历温度数据，idx 是天数（从1开始），temp 是当天温度
    for idx, temp in enumerate(temperature, 1):
        # 数学原理：当 t=1 时，S₁ = Y₁（第一天的 EWA 等于当天温度）
        if idx == 1:
            # 将第一天的温度加入 EWA 结果列表
            exp_weight_avg.append(temp)
            # 跳过后续逻辑，直接处理下一天
            continue
        
        # 数学公式：Sₜ = β·Sₜ₋₁ + (1 - β)·Yₜ
        # exp_weight_avg[idx-2] 是 Sₜ₋₁（前一天的 EWA 结果）
        new_temp = exp_weight_avg[idx - 2] * beta + (1 - beta) * temp
        # 将当天的 EWA 结果加入列表
        exp_weight_avg.append(new_temp)
    
    # 生成 x 轴坐标：1~30 天
    days = torch.arange(1, ELEMENT_NUMBER + 1, 1)
    # 绘制 EWA 平滑后的曲线（红色折线）
    plt.plot(days, exp_weight_avg, color='r')
    # 绘制原始温度散点（对比平滑效果）
    plt.scatter(days, temperature)
    # 显示图形（弹出窗口展示平滑结果）
    plt.show()
test02()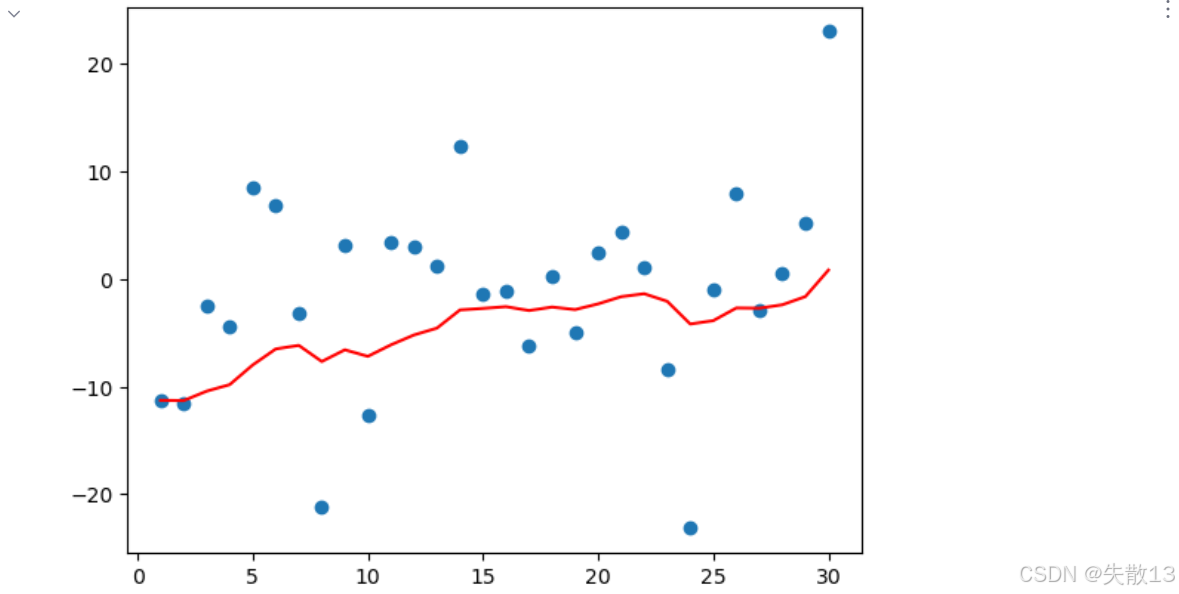

• 上图：指数加权平均的 "平滑效果"

  • 蓝点 ：和左图完全相同的原始温度数据 （因为代码里 torch.manual_seed(0) 固定了随机数，确保数据一致）；
  • 红线 ：指数加权平均后的温度趋势 （代码里用 Sₜ = β·Sₜ₋₁ + (1 - β)·Yₜ 计算，默认 β=0.9）；

• 平滑效果的核心逻辑：

  1. 近期数据权重更高：比如第 30 天的极端高温，会被前 29 天的平均结果 "拉平"，所以红线不会像左图一样突然飙升；
  2. 过滤噪声，保留趋势：红线能大致跟随温度的 "整体变化方向"（比如前期降温、中期平稳、后期缓慢升温），但过滤了单日的极端波动（如第 8 天、第 25 天的极低值）。

3.5.3 方法2：动量优化算法Momentum

3.5.3.1 概述

• 动量优化算法（Momentum），核心解决"普通梯度下降易卡壳、震荡大"的问题；

• 类比"物理动量"：给梯度下降加"惯性"，让参数更新更顺滑。计算带动量的梯度DtD_tDt （替代普通梯度WtW_tWt用于参数更新）：
  Dt=β⋅St−1+(1−β)⋅Wt D_t = \beta \cdot S_{t-1} + (1 - \beta) \cdot W_t Dt=β⋅St−1+(1−β)⋅Wt

  • DtD_tDt：当前时刻的动量梯度（用于参数更新的"平滑后梯度"）

  • St−1S_{t-1}St−1：历史梯度的加权平均（前一时刻的动量梯度，体现"惯性"）

  • WtW_tWt：当前时刻的原始梯度（普通梯度下降用的梯度）

  • β\betaβ：动量系数（如 0.9，控制"历史梯度的影响力"，越大惯性越强）

• 假设β=0.9\beta=0.9β=0.9，梯度更新会叠加"历史惯性"：

  • 第一次（t=1t=1t=1）：D1=W1D_1 = W_1D1=W1（无历史，直接用当前梯度）
  • 第二次（t=2t=2t=2）：D2=0.9⋅D1+0.1⋅W2D_2 = 0.9 \cdot D_1 + 0.1 \cdot W_2D2=0.9⋅D1+0.1⋅W2（历史梯度占 90%，当前占 10%）
  • 第三次（t=3t=3t=3）：D3=0.9⋅D2+0.1⋅W3D_3 = 0.9 \cdot D_2 + 0.1 \cdot W_3D3=0.9⋅D2+0.1⋅W3（惯性继续传递）
  • ...... 以此类推，梯度更新会保留"历史趋势"

• 梯度下降公式中梯度的计算，就不再是当前时刻ttt的梯度值，而是历史梯度值的指数移动加权平均值。公式修改为：
  Wt+1=Wt−α⋅Dt W_{t+1} = W_t - \alpha \cdot D_t Wt+1=Wt−α⋅Dt

  • α\alphaα：学习率（步长）；

  • 本质：让参数更新方向不仅看"当前梯度"，还叠加"历史趋势"，避免被局部波动带偏；

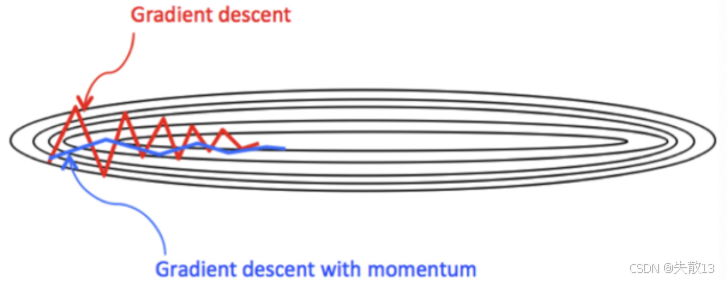
• Monmentum 优化方法是如何一定程度上克服卡鞍点、震荡大的问题呢？

  

  • 跨越鞍点（梯度为 0 时不停滞）

    • 普通梯度下降 ：遇到鞍点（梯度Wt=0W_t=0Wt=0），参数更新直接停住，无法找到更优解

    • 动量算法 ：靠历史积累的DtD_tDt（非零），让参数"惯性前进"，有机会跳过鞍点，继续找全局最优

  • 平滑震荡（让更新方向更稳定）

    • 普通梯度下降（mini-batch）：用少量样本算梯度，易导致参数更新"震荡大、方向乱"（如图中红色折线）

    • 动量算法 ：通过DtD_tDt对梯度做"指数加权平均"，过滤局部波动，让更新方向更平滑（如图中蓝色折线），加速训练且更稳定

3.5.3.2 代码

def test03():
    # 1. 初始化权重参数
    # 创建一个张量 w，值为 [1.0]，开启自动求导（requires_grad=True），数据类型为 float32
    # 这个张量会被用于模拟神经网络中的可学习参数（如权重）
    w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
    # 定义一个简单的计算图：y = (w*2)/2.0 的总和（实际等价于 y = w，但用复杂计算模拟前向传播）
    # 这里的计算会构建梯度反向传播的依赖关系
    y = ((w ** 2) / 2.0).sum()

    # 2. 实例化优化方法：SGD + 动量（momentum=0.9）
    # 优化器负责更新参数 w，学习率 lr=0.01，动量系数 beta=0.9
    # 动量会让参数更新时参考历史梯度，避免震荡并加速收敛
    optimizer = torch.optim.SGD([w], lr=0.01, momentum=0.9)

    # 3. 第1次更新：计算梯度 + 参数更新
    # 梯度清零：PyTorch 会累积梯度，反向传播前必须手动清零，避免影响本次计算
    optimizer.zero_grad()
    # 反向传播：自动计算 y 对 w 的梯度（dy/dw），并把梯度存到 w.grad 中
    y.backward()
    # 执行参数更新：根据动量优化器规则，用梯度更新 w 的值
    optimizer.step()

    # 打印第1次更新的结果
    # w.grad.numpy()：取出 w 的梯度（dy/dw）转成 numpy 数组
    # w.detach().numpy()：取出 w 的值（ detach 避免影响计算图）转成 numpy 数组
    print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))

    # 4. 第2次更新：使用更新后的参数重新计算 + 更新
    # 重新计算前向传播（用更新后的 w 计算新的 y）
    y = ((w ** 2) / 2.0).sum()
    # 梯度清零：准备第二次反向传播
    optimizer.zero_grad()
    # 反向传播：再次计算新的梯度（基于更新后的 w）
    y.backward()
    # 执行第二次参数更新（动量会结合历史梯度）
    optimizer.step()

    # 打印第2次更新的结果（逻辑同第一次）
    print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
test03()

• 第1次更新

  • 梯度 w.grad=1.0 ：反向传播计算得 y 对 w 的导数为 1（因为 y = w²/2，导数 dy/dw = w，初始 w=1.0，所以梯度是 1）；

  • 更新后权重 0.99 ：优化器用动量 SGD 更新参数，公式为：
    wnew=wold−lr×grad w_{\text{new}} = w_{\text{old}} - \text{lr} \times \text{grad} wnew=wold−lr×grad

  • 代入 w=1.0, lr=0.01, grad=1，得 1.0 - 0.01×1 = 0.99；

• 第2次更新

  • 梯度 w.grad=0.99 ：反向传播时，w 已更新为 0.99，所以导数 dy/dw = 0.99（同样因为 y = w²/2，导数是当前 w 的值）；

  • 更新后权重 0.9711 ：动量优化器会结合历史梯度 （第一次的梯度）和当前梯度，使用动量公式更新权重；

    • 具体更新公式为：
      vnew=β⋅vold+(1−β)⋅grad v_{\text{new}} = \beta \cdot v_{\text{old}} + (1 - \beta) \cdot \text{grad} vnew=β⋅vold+(1−β)⋅grad

      • 其中vold=0.1v_{\text{old}} = 0.1vold=0.1是第一次更新时的动量，当前的梯度为0.990.990.99，动量系数β=0.9\beta = 0.9β=0.9；

    • 计算新的动量项：
      vnew=0.9⋅0.1+0.1⋅0.99=0.09+0.099=0.189 v_{\text{new}} = 0.9 \cdot 0.1 + 0.1 \cdot 0.99 = 0.09 + 0.099 = 0.189 vnew=0.9⋅0.1+0.1⋅0.99=0.09+0.099=0.189

    • 然后，使用学习率lr=0.01\text{lr} = 0.01lr=0.01更新权重：
      wnew=wold−lr×vnew w_{\text{new}} = w_{\text{old}} - \text{lr} \times v_{\text{new}} wnew=wold−lr×vnew

    • 代入当前的wold=0.99w_{\text{old}} = 0.99wold=0.99，动量vnew=0.189v_{\text{new}} = 0.189vnew=0.189和学习率lr=0.01\text{lr} = 0.01lr=0.01，计算得到：
      wnew=0.99−0.01×0.189=0.99−0.00189=0.9711 w_{\text{new}} = 0.99 - 0.01 \times 0.189 = 0.99 - 0.00189 = 0.9711 wnew=0.99−0.01×0.189=0.99−0.00189=0.9711

3.5.4 方法3：AdaGrad算法

3.5.4.1 概述

• AdaGrad 优化算法 ：核心是 "自适应调整学习率"，让不同参数按自身梯度历史动态调整更新步长；

• 普通的梯度下降 （Gradient Descent）使用一个固定的学习率 ，这个学习率对所有的参数更新都是相同的。而AdaGrad 则让每个参数有独立的学习率，根据每个参数的历史梯度来调整其学习率。这意味着：

  • 梯度大的参数会导致学习率快速衰减，从而避免因过大的更新导致模型不稳定或震荡；
  • 梯度小的参数会让学习率衰减较慢，允许对这些参数进行更细致的调整；

• 本质是用"历史梯度的平方和"做学习率的分母，让学习率随训练逐步减小，且不同参数衰减速度不同；

• 计算步骤：

  1. 初始化

     • 学习率α\alphaα（全局初始值，如 0.01）、参数θ\thetaθ（要更新的权重/偏置）、小常数σ=10−6\sigma=10^{-6}σ=10−6（避免分母为 0）；

     • 梯度累积变量s=0s=0s=0（记录历史梯度的平方和）；

  2. 计算梯度ggg ：从训练数据中采样，计算参数θ\thetaθ的梯度g=∂Loss∂θg = \frac{\partial \text{Loss}}{\partial \theta}g=∂θ∂Loss（反向传播求导）；

  3. 累积平方梯度sss
     s=s+g⊙g s = s + g \odot g s=s+g⊙g

     • ⊙\odot⊙是逐元素相乘 （每个参数的梯度平方累加到sss对应位置）；

     • 作用：记录每个参数的"历史梯度大小"，梯度大的参数，sss增长快，后续学习率衰减多；

  4. 计算"自适应学习率"
     学习率=αs+σ \text{学习率} = \frac{\alpha}{\sqrt{s} + \sigma} 学习率=s +σα

     • 分母是s+σ\sqrt{s} + \sigmas +σ：
       • s\sqrt{s}s 随训练逐步增大（因为sss累积梯度平方），让学习率全局衰减；
       • σ\sigmaσ是小常数（如10−610^{-6}10−6），避免s=0\sqrt{s}=0s =0时分母为 0；

  5. 参数更新
     θ=θ−αs+σ⋅g \theta = \theta - \frac{\alpha}{\sqrt{s} + \sigma} \cdot g θ=θ−s +σα⋅g

     • 用"自适应学习率"替代固定学习率，让参数更新步长动态调整：
       • 梯度大的参数（sss大 ）→ 学习率小 → 步长小（避免震荡）；
       • 梯度小的参数（sss小 ）→ 学习率大 → 步长大（更灵活调整）；

  6. 循环迭代：重复"算梯度 → 累平方 → 更学习率 → 更参数"，直到训练结束；

• 优点：自适应学习率

  • 对不同参数"因材施教"：梯度大的参数（如分类任务中区分度高的特征）学习率衰减快，梯度小的参数（区分度低的特征）学习率衰减慢;

  • 适合处理稀疏数据（如文本分类，部分特征梯度小但重要，需更慢衰减）；

• 缺点：学习率"过度衰减"

  • sss是累积平方和 ，训练后期sss会非常大 → 学习率αs+σ\frac{\alpha}{\sqrt{s} + \sigma}s +σα趋近于 0 → 参数几乎不更新，模型"学不动"，难收敛到全局最优。

3.5.4.2 代码

def test04():
    # 1. 初始化权重参数
    # 创建可训练参数 w，初始值为 1.0，开启自动求导（requires_grad=True）
    # 这是要优化的目标参数，模拟神经网络中的权重
    w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
    # 定义简单计算图：y = (w²)/2（模拟前向传播的损失计算）
    # 后续反向传播会基于此计算梯度
    y = ((w ** 2) / 2.0).sum()

    # 2. 实例化优化方法：AdaGrad 优化器
    # AdaGrad 的核心是「自适应学习率」，会根据历史梯度调整更新步长
    # lr=0.01 是初始学习率，优化器会自动维护学习率的衰减
    optimizer = torch.optim.Adagrad([w], lr=0.01)

    # 3. 第1次更新：计算梯度 + 参数更新
    # 梯度清零：PyTorch 会累积梯度，反向传播前必须手动清零
    optimizer.zero_grad()
    # 反向传播：自动计算 y 对 w 的梯度（dy/dw = w），结果存到 w.grad
    y.backward()
    # 执行参数更新：AdaGrad 会用「历史梯度平方和」调整学习率，更新 w
    optimizer.step()

    # 打印第1次更新结果
    # w.grad.numpy()：取出梯度值（转成 NumPy 数组）
    # w.detach().numpy()：取出 w 的当前值（detach 断开计算图，避免影响反向传播）
    print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))

    # 4. 第2次更新：用更新后的参数重新计算 + 更新
    # 重新前向传播：用新的 w 计算 y（模拟下一轮训练）
    y = ((w ** 2) / 2.0).sum()
    # 梯度清零：准备第二次反向传播
    optimizer.zero_grad()
    # 反向传播：计算新的梯度（基于更新后的 w）
    y.backward()
    # 执行第二次参数更新（AdaGrad 会继续累积历史梯度，调整学习率）
    optimizer.step()

    # 打印第2次更新结果（逻辑同第一次）
    print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
test04()

• 第1次更新

  • 梯度计算：反向传播计算得 w.grad=1.0（因为 y = w²/2，导数 dy/dw = w，初始 w=1.0，所以梯度是 1.0 ）；

  • AdaGrad 的更新逻辑：AdaGrad 内部维护历史梯度平方和 s （初始为 0）

    • 累积平方梯度：s = s + (w.grad)² = 0 + 1.0² = 1.0

    • 计算自适应学习率：
      lrcurrent=初始 lrs+σ=0.011.0+10−6≈0.01 \text{lr}_{\text{current}} = \frac{\text{初始 lr}}{\sqrt{s} + \sigma} = \frac{0.01}{\sqrt{1.0} + 10^{-6}} \approx 0.01 lrcurrent=s +σ初始 lr=1.0 +10−60.01≈0.01

    • 参数更新：
      w=w−lrcurrent×w.grad=1.0−0.01×1.0=0.99 w = w - \text{lr}_{\text{current}} \times w.grad = 1.0 - 0.01 \times 1.0 = 0.99 w=w−lrcurrent×w.grad=1.0−0.01×1.0=0.99

• 第2次更新（体现 AdaGrad 特性）

  • 梯度计算：参数更新后 w=0.99，重新计算梯度

    • 前向传播：y = (0.99²)/2 ≈ 0.49005

    • 反向传播：w.grad=0.99（因为 dy/dw = w = 0.99 ）

  • AdaGrad 的更新逻辑：此时 AdaGrad 内部的 s 已累积历史梯度

    • 累积平方梯度：s = 1.0 + (0.99)² = 1.0 + 0.9801 = 1.9801

    • 计算自适应学习率：
      lrcurrent=0.011.9801+10−6≈0.011.407≈0.00709 \text{lr}_{\text{current}} = \frac{0.01}{\sqrt{1.9801} + 10^{-6}} \approx \frac{0.01}{1.407} \approx 0.00709 lrcurrent=1.9801 +10−60.01≈1.4070.01≈0.00709

    • 参数更新：和输出 0.982965 细微差异是浮点运算精度问题
      w=0.99−0.00709×0.99≈0.99−0.00702=0.98298 w = 0.99 - 0.00709 \times 0.99 \approx 0.99 - 0.00702 = 0.98298 w=0.99−0.00709×0.99≈0.99−0.00702=0.98298

• 对比两次更新

  1. 学习率衰减 ：第一次学习率≈0.01，第二次≈0.00709，学习率随 s 增大而衰减（s 是历史梯度平方和）；

  2. 自适应步长 ：梯度大的参数（第一次 w.grad=1.0 ），学习率衰减快；梯度变小后（第二次 w.grad=0.99 ），学习率衰减慢，但总体趋势是逐步减小。

3.5.5 方法4：RMSProp算法

3.5.5.1 概述

• RMSProp 优化算法，核心是对 AdaGrad 的改进（用"指数移动平均"替代"历史梯度平方和"），解决其"学习率衰减过快"的问题；

• AdaGrad 的问题 ：历史梯度平方和 s 会持续累加，导致学习率后期趋近于 0，模型无法更新；

• RMSProp 的改进 ：用 指数移动平均（EMA） 计算 s，公式如下
  s=β⋅s+(1−β)⋅g⊙g s = \beta \cdot s + (1 - \beta) \cdot g \odot g s=β⋅s+(1−β)⋅g⊙g

  • β\betaβ是动量系数（如 0.9 ），控制"历史梯度的权重"；

  • g⊙gg \odot gg⊙g是当前梯度的平方（逐元素相乘）；

• 效果 ：让 s 更关注近期梯度（历史梯度的影响指数级衰减），避免学习率过快衰减；

• 计算步骤：

  1. 初始化

     • 学习率α\alphaα（如 0.01 ）、参数θ\thetaθ（要更新的权重/偏置 ）、小常数σ=10−6\sigma=10^{-6}σ=10−6（避免分母为 0）；

     • 梯度累积变量s=0s=0s=0（初始为 0 ，用指数移动平均更新）；

  2. 计算梯度ggg：从训练数据中采样，计算参数θ\thetaθ的梯度g=∂Loss∂θg = \frac{\partial \text{Loss}}{\partial \theta}g=∂θ∂Loss（反向传播求导）；

  3. 指数移动平均更新sss
     s=β⋅s+(1−β)⋅g⊙g s = \beta \cdot s + (1 - \beta) \cdot g \odot g s=β⋅s+(1−β)⋅g⊙g

     • 用当前梯度平方更新sss，但历史梯度的权重随β\betaβ指数衰减；

     • 例如：β=0.9\beta=0.9β=0.9时，当前梯度占 10%，历史梯度占 90%（但历史梯度是"衰减后的历史"）；

  4. 计算"自适应学习率"
     学习率=αs+σ \text{学习率} = \frac{\alpha}{\sqrt{s} + \sigma} 学习率=s +σα

     • 分母是s+σ\sqrt{s} + \sigmas +σ：
       • sss是"近期梯度平方的加权平均"，避免了 AdaGrad 中sss持续累加的问题；
       • σ\sigmaσ是小常数，避免分母为 0；

  5. 参数更新：用"自适应学习率"更新参数，步长由近期梯度的平均决定，更稳定；
     θ=θ−αs+σ⋅g \theta = \theta - \frac{\alpha}{\sqrt{s} + \sigma} \cdot g θ=θ−s +σα⋅g

  6. 循环迭代：重复"计算梯度 → 更新sss→ 调整学习率 → 更新参数"，直到训练结束；

• 对比 AdaGrad：

  • 学习率更稳定 ：用指数移动平均让sss关注近期梯度，避免学习率后期趋近于 0；
  • 平衡历史与当前梯度 ：β\betaβ控制历史梯度的权重，可灵活调整"对历史趋势的关注程度"。

3.5.5.2 代码

def test05():
    # 1. 初始化权重参数
    # 创建一个形状为 [1] 的张量 w，初始值为 1.0，开启自动求导功能，数据类型为 float32
    # 该张量用于模拟神经网络中可学习的参数（如权重），后续会通过优化器进行更新
    w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
    # 定义一个简单的计算图，计算 y 的值，这里 y = (w²) / 2 ，sum 用于将结果转为标量（因 w 是单元素张量，sum 不改变值但符合计算图构建逻辑）
    # 后续反向传播会基于此计算图来计算 w 的梯度
    y = ((w ** 2) / 2.0).sum()

    # 2. 实例化优化方法：RMSProp 优化器
    # RMSProp 是 AdaGrad 的改进版，通过指数移动平均来调整学习率，避免学习率衰减过快的问题
    # [w] 表示要优化的参数列表，lr=0.01 是初始学习率，alpha=0.9 是指数移动平均的衰减系数（对应原理中的 β）
    # alpha 越大，历史梯度对当前更新的影响越持久；alpha 越小，越关注近期梯度
    optimizer = torch.optim.RMSprop([w], lr=0.01, alpha=0.9)

    # 3. 第 1 次更新：计算梯度并更新参数
    # 梯度清零操作，因为 PyTorch 中梯度会累加，在每次反向传播前需要手动清零，避免之前的梯度影响当前计算
    optimizer.zero_grad()
    # 反向传播过程，自动根据计算图计算 y 对 w 的梯度，结果会存储在 w.grad 中
    y.backward()
    # 执行参数更新步骤，RMSProp 优化器会根据当前梯度、历史梯度的指数移动平均结果来调整学习率并更新 w 的值
    optimizer.step()

    # 打印第 1 次更新后的结果
    # w.grad.numpy() 用于获取 w 的梯度值并转换为 numpy 数组（方便打印查看）
    # w.detach().numpy() 用于获取 w 的当前值并转换为 numpy 数组（detach 是为了断开与计算图的连接，避免影响后续计算图，同时能安全地转换为 numpy 数组）
    print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))

    # 4. 第 2 次更新：使用更新后的参数重新计算并更新
    # 重新计算前向传播，此时 w 已经是第 1 次更新后的值，计算新的 y 值，用于再次反向传播
    y = ((w ** 2) / 2.0).sum()
    # 再次梯度清零，准备第二次反向传播
    optimizer.zero_grad()
    # 第二次反向传播，计算新的梯度（基于更新后的 w ）
    y.backward()
    # 第二次执行参数更新，RMSProp 会继续结合新的梯度和历史梯度的指数移动平均结果来调整 w 
    optimizer.step()

    # 打印第 2 次更新后的结果，查看梯度和参数的变化情况
    print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
test05()

• 第1次更新

  1. 梯度计算：反向传播计算得 w.grad=1.0（因为 y = w²/2，导数 dy/dw = w = 1.0 ）；

  2. RMSProp 的更新逻辑：RMSProp 内部维护指数移动平均变量 s （初始为 0 ），公式
     s=β⋅s+(1−β)⋅(w.grad)2 s = \beta \cdot s + (1 - \beta) \cdot (w.grad)^2 s=β⋅s+(1−β)⋅(w.grad)2

     （β=0.9 是代码中 alpha=0.9，控制历史梯度的权重）

  • 第一次更新时：

    • 计算 s：
      s=0.9×0+(1−0.9)×(1.0)2=0.1 s = 0.9 \times 0 + (1 - 0.9) \times (1.0)^2 = 0.1 s=0.9×0+(1−0.9)×(1.0)2=0.1

    • 计算自适应学习率：
      lrcurrent=初始 lrs+ϵ=0.010.1+10−6≈0.0316 \text{lr}_{\text{current}} = \frac{\text{初始 lr}}{\sqrt{s} + \epsilon} = \frac{0.01}{\sqrt{0.1} + 10^{-6}} \approx 0.0316 lrcurrent=s +ϵ初始 lr=0.1 +10−60.01≈0.0316

    • 参数更新：
      w=1.0−0.0316×1.0=0.9684 w = 1.0 - 0.0316 \times 1.0 = 0.9684 w=1.0−0.0316×1.0=0.9684

      （和输出 0.968377 细微差异是浮点运算精度问题）

• 第2次更新（体现 RMSProp 特性）

  1. 梯度计算：参数更新后 w≈0.968377，重新计算梯度

     • 前向传播：y = (0.968377²)/2 ≈ 0.468

     • 反向传播：w.grad=0.968377（因为 dy/dw = w = 0.968377 ）。

  2. RMSProp 的更新逻辑：此时 RMSProp 内部的 s 已用指数移动平均更新

     • 计算新的 s：
       s=0.9×0.1+(1−0.9)×(0.968377)2≈0.9×0.1+0.1×0.9377=0.18377 s = 0.9 \times 0.1 + (1 - 0.9) \times (0.968377)^2 \approx 0.9 \times 0.1 + 0.1 \times 0.9377 = 0.18377 s=0.9×0.1+(1−0.9)×(0.968377)2≈0.9×0.1+0.1×0.9377=0.18377

     • 计算自适应学习率：
       lrcurrent=0.010.18377+10−6≈0.010.4287≈0.0233 \text{lr}_{\text{current}} = \frac{0.01}{\sqrt{0.18377} + 10^{-6}} \approx \frac{0.01}{0.4287} \approx 0.0233 lrcurrent=0.18377 +10−60.01≈0.42870.01≈0.0233

  • 参数更新：
    w=0.968377−0.0233×0.968377≈0.968377−0.0226=0.94577 w = 0.968377 - 0.0233 \times 0.968377 \approx 0.968377 - 0.0226 = 0.94577 w=0.968377−0.0233×0.968377≈0.968377−0.0226=0.94577
    （和输出 0.945788 一致，浮点精度差异）

• 对比两次更新

  1. 学习率衰减更平缓 ：用指数移动平均后，s 更关注近期梯度，避免了 AdaGrad 中学习率"断崖式衰减"的问题；

  2. 自适应步长 ：梯度大的参数（第一次 w.grad=1.0），学习率衰减慢；梯度变小后（第二次 w.grad=0.968），学习率继续衰减，但衰减速度由 β 控制 （β=0.9 时衰减平缓）。

3.5.6 方法5：Adam算法

3.5.6.1 概述

• Adam 优化算法，核心逻辑是**"结合 Momentum（动量）和 RMSProp（自适应学习率）的优点"**，融合了这两种经典优化器：

  优化器	核心能力	缺点
  Momentum	用指数加权平均加速梯度更新（惯性）	无法自适应调整学习率
  RMSProp	用指数加权平均自适应调整学习率	缺少"惯性加速"的特性

• Adam 的创新：同时做两件事

  1. 修正梯度（类似 Momentum）：用指数加权平均平滑梯度，避免震荡；
  2. 修正学习率（类似 RMSProp）：用指数加权平均调整学习率，避免衰减过快；

• Adam 的两大核心步骤

  1. 修正梯度（对应 Momentum 的惯性）。用指数加权平均 计算梯度的"动量"，公式：
     mt=β1⋅mt−1+(1−β1)⋅gt m_t = \beta_1 \cdot m_{t-1} + (1 - \beta_1) \cdot g_t mt=β1⋅mt−1+(1−β1)⋅gt

     • mtm_tmt：当前梯度的"动量修正值"（融合历史梯度的方向）；

     • β1\beta_1β1：动量系数（如 0.9 ），控制历史梯度的权重；

     • 作用：让梯度更新更平滑（类似 Momentum 的"惯性"，加速收敛）；

  2. 修正学习率（对应 RMSProp 的自适应）。用指数加权平均 计算梯度平方的"学习率修正值"，公式：
     vt=β2⋅vt−1+(1−β2)⋅gt2 v_t = \beta_2 \cdot v_{t-1} + (1 - \beta_2) \cdot g_t^2 vt=β2⋅vt−1+(1−β2)⋅gt2

     • vtv_tvt：当前梯度平方的"学习率修正值"（融合历史梯度的大小）；

     • β2\beta_2β2：学习率系数（如 0.999 ），控制历史梯度平方的权重；

     • 作用：让学习率自适应调整（类似 RMSProp，避免震荡）。

3.5.6.2 代码

def test06():
    # 1. 初始化权重参数
    # 创建一个形状为 [1] 的张量 w，初始值为 1.0，开启自动求导功能
    # 该张量用于模拟神经网络中可学习的参数（如权重），后续会通过 Adam 优化器进行更新
    w = torch.tensor([1.0], requires_grad=True)
    # 定义一个简单的计算图，计算 y 的值，这里 y = (w²) / 2 ，sum 用于将结果转为标量（因 w 是单元素张量，sum 不改变值但符合计算图构建逻辑）
    # 后续反向传播会基于此计算图来计算 w 的梯度
    y = ((w ** 2) / 2.0).sum()

    # 2. 实例化优化方法：Adam 优化器
    # Adam 优化器结合了 Momentum（动量，用 betas[0]=0.9 控制）和 RMSProp（自适应学习率，用 betas[1]=0.99 控制）的优点
    # [w] 表示要优化的参数列表，lr=0.01 是初始学习率
    # betas=[0.9, 0.99] 中，第一个值控制梯度的指数移动平均（动量部分），第二个值控制梯度平方的指数移动平均（自适应学习率部分）
    optimizer = torch.optim.Adam([w], lr=0.01, betas=[0.9, 0.99])

    # 3. 第 1 次更新：计算梯度并更新参数
    # 梯度清零操作，因为 PyTorch 中梯度会累加，在每次反向传播前需要手动清零，避免之前的梯度影响当前计算
    optimizer.zero_grad()
    # 反向传播过程，自动根据计算图计算 y 对 w 的梯度，结果会存储在 w.grad 中
    y.backward()
    # 执行参数更新步骤，Adam 优化器会结合当前梯度、梯度的动量平均结果、梯度平方的自适应平均结果来调整学习率并更新 w 的值
    optimizer.step()

    # 打印第 1 次更新后的结果
    # w.grad.numpy() 用于获取 w 的梯度值并转换为 numpy 数组（方便打印查看）
    # w.detach().numpy() 用于获取 w 的当前值并转换为 numpy 数组（detach 是为了断开与计算图的连接，避免影响后续计算图，同时能安全地转换为 numpy 数组）
    print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))

    # 4. 第 2 次更新：使用更新后的参数重新计算并更新
    # 重新计算前向传播，此时 w 已经是第 1 次更新后的值，计算新的 y 值，用于再次反向传播
    y = ((w ** 2) / 2.0).sum()
    # 梯度清零操作，准备第二次反向传播
    optimizer.zero_grad()
    # 第二次反向传播过程，自动根据新的计算图计算 y 对 w 的梯度，结果存储在 w.grad 中
    y.backward()
    # 执行第二次参数更新步骤，Adam 优化器继续结合最新的梯度等信息，按照其内部逻辑（动量 + 自适应学习率）更新 w 的值
    optimizer.step()

    # 打印第 2 次更新后的结果，查看梯度和参数的变化情况
    print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
test06()

• 第1次更新

  1. 梯度计算：反向传播计算得 w.grad=1.0（因为 y = w²/2，导数 dy/dw = w = 1.0 ）；

  2. Adam 的更新逻辑。Adam 内部维护两个关键变量：

     • 动量梯度 m （指数加权平均梯度，对应 β₁=0.9 ）

     • 梯度平方的平均 v （指数加权平均梯度平方，对应 β₂=0.99 ）

  3. 第一次更新时：

     • 动量梯度 m：
       m1=β1⋅m0+(1−β1)⋅g1=0.9×0+0.1×1.0=0.1 m_1 = \beta_1 \cdot m_0 + (1 - \beta_1) \cdot g_1 = 0.9 \times 0 + 0.1 \times 1.0 = 0.1 m1=β1⋅m0+(1−β1)⋅g1=0.9×0+0.1×1.0=0.1

     • 梯度平方平均 v：
       v1=β2⋅v0+(1−β2)⋅g12=0.99×0+0.01×1.02=0.01 v_1 = \beta_2 \cdot v_0 + (1 - \beta_2) \cdot g_1^2 = 0.99 \times 0 + 0.01 \times 1.0^2 = 0.01 v1=β2⋅v0+(1−β2)⋅g12=0.99×0+0.01×1.02=0.01

     • 偏差修正 （因初始 m_0=0, v_0=0，前几步需修正）：
       m1^=m11−β11=0.10.1=1.0v1^=v11−β21=0.010.01=1.0 \hat{m_1} = \frac{m_1}{1 - \beta_1^1} = \frac{0.1}{0.1} = 1.0 \\ \hat{v_1} = \frac{v_1}{1 - \beta_2^1} = \frac{0.01}{0.01} = 1.0 m1^=1−β11m1=0.10.1=1.0v1^=1−β21v1=0.010.01=1.0

     • 参数更新 ：
       w1=w0−lr⋅m1^v1^+ϵ=1.0−0.01×1.01.0+10−8≈0.99 w_1 = w_0 - \text{lr} \cdot \frac{\hat{m_1}}{\sqrt{\hat{v_1}} + \epsilon} = 1.0 - 0.01 \times \frac{1.0}{1.0 + 10^{-8}} \approx 0.99 w1=w0−lr⋅v1^ +ϵm1^=1.0−0.01×1.0+10−81.0≈0.99

• 第2次更新（体现 Adam 特性）

  1. 梯度计算。参数更新后 w≈0.99，重新计算梯度：

     • 前向传播：y = (0.99²)/2 ≈ 0.49005

     • 反向传播：w.grad=0.99（因为 dy/dw = w = 0.99）

  2. Adam 的更新逻辑。第二次更新时，Adam 继续维护 m 和 v：

     • 动量梯度 m：
       m2=β1⋅m1+(1−β1)⋅g2=0.9×0.1+0.1×0.99=0.189 m_2 = \beta_1 \cdot m_1 + (1 - \beta_1) \cdot g_2 = 0.9 \times 0.1 + 0.1 \times 0.99 = 0.189 m2=β1⋅m1+(1−β1)⋅g2=0.9×0.1+0.1×0.99=0.189

     • 梯度平方平均 v：
       v2=β2⋅v1+(1−β2)⋅g22=0.99×0.01+0.01×0.992=0.01+0.009801=0.019801 v_2 = \beta_2 \cdot v_1 + (1 - \beta_2) \cdot g_2^2 = 0.99 \times 0.01 + 0.01 \times 0.99^2 = 0.01 + 0.009801 = 0.019801 v2=β2⋅v1+(1−β2)⋅g22=0.99×0.01+0.01×0.992=0.01+0.009801=0.019801

     • 偏差修正 （t=2 时 ）：
       m2^=m21−β12=0.1891−0.81=0.1890.19≈0.9947v2^=v21−β22=0.0198011−0.9801=0.0198010.0199≈0.995 \hat{m_2} = \frac{m_2}{1 - \beta_1^2} = \frac{0.189}{1 - 0.81} = \frac{0.189}{0.19} \approx 0.9947 \\ \hat{v_2} = \frac{v_2}{1 - \beta_2^2} = \frac{0.019801}{1 - 0.9801} = \frac{0.019801}{0.0199} \approx 0.995 m2^=1−β12m2=1−0.810.189=0.190.189≈0.9947v2^=1−β22v2=1−0.98010.019801=0.01990.019801≈0.995

     • 参数更新 ：
       w2=w1−lr⋅m2^v2^+ϵ=0.99−0.01×0.99470.9975≈0.980003 w_2 = w_1 - \text{lr} \cdot \frac{\hat{m_2}}{\sqrt{\hat{v_2}} + \epsilon} = 0.99 - 0.01 \times \frac{0.9947}{0.9975} \approx 0.980003 w2=w1−lr⋅v2^ +ϵm2^=0.99−0.01×0.99750.9947≈0.980003

• 对比两次更新

  1. 动量加速 ：用 m 累积历史梯度方向，让更新更平滑（第一次到第二次，梯度从 1.0 降到 0.99，但更新步长因动量保持稳定）；

  2. 自适应学习率 ：用 v 累积历史梯度平方，避免学习率"一刀切"，让梯度大的参数（第一次 w.grad=1.0 ）学习率衰减更合理；

  3. 偏差修正 ：前几步修正 m 和 v，避免初始值为 0 导致的更新延迟，加速收敛。

3.6 学习率衰减方法

3.6.1 概述

• 让学习率衰减是深度学习训练中非常重要的策略，核心目的是平衡模型的"探索效率"和"收敛精度"；

• 训练初期：需要较大的学习率快速探索

  • 模型训练初期，参数处于随机初始化状态，离最优解较远；
  • 较大的学习率能让参数"大步跨越"，快速向损失较低的区域靠近，加快收敛速度（避免陷入缓慢的局部探索）；
  • 例如：初始学习率设为0.1，参数更新幅度大，能快速从随机值向合理范围逼近；

• 训练后期：需要较小的学习率精细调整

  • 当模型接近最优解时，参数已经在较优区域附近；

  • 如果继续使用大学习率，可能导致参数在最优解附近"震荡"（步子太大，跳过最优值），无法稳定收敛到最小值；

  • 衰减学习率后（比如降到0.01、0.001），参数更新幅度变小，能在最优解附近"小步微调"，逐步逼近更精确的结果；

• 避免过拟合风险

  • 训练后期，模型可能开始"记住"训练数据的细节（包括噪声），导致过拟合；

  • 较小的学习率能降低参数的"敏感程度"，让模型更关注数据的整体规律而非细节噪声，提高泛化能力。

3.6.2 等间隔学习率衰减

3.6.2.1 概述

• 等间隔学习率衰减（Step LR Scheduler），核心是按固定周期降低学习率，帮模型训练更稳定、效果更好；

• 核心逻辑：学习率（lr）是模型更新参数的"步长"，训练前期用大学习率快速逼近最优解，后期用小学习率精细调整。等间隔衰减 就是每隔 step_size 个训练周期（Epoch），把学习率乘以 gamma（如 lr = lr * gamma ），让步长逐步缩小；

• API：

  lr_scheduler.StepLR(optimizer, step_size, gamma=0.1)

  • optimizer：要调整学习率的优化器（如 Adam、SGD），告诉算法 "改谁的学习率"；

  • step_size：调整间隔，比如设 50，就每训练 50 个 Epoch 衰减一次学习率；

  • gamma：衰减系数，比如 0.5，每次衰减后学习率变成原来的 50% ；设 0.1 就是变成 10% ，控制衰减幅度；

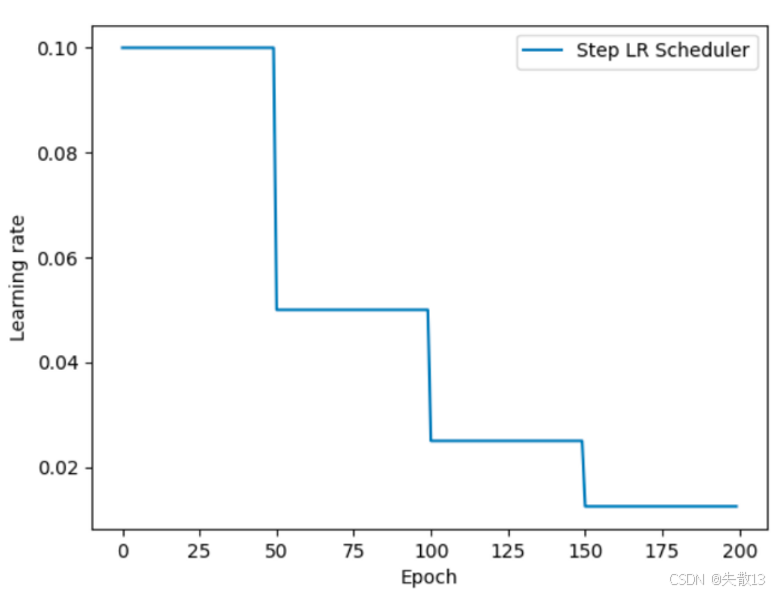
• 下面折线图直观展示学习率随 Epoch 的变化：

  

  • 前 50 个 Epoch ，学习率保持初始值（比如 0.1）；

  • 到第 50 个 Epoch ，学习率乘以 gamma 衰减（比如变成 0.05）；

  • 再到 100、150 Epoch ，重复衰减，逐步缩小步长，适配模型后期精细训练；

• 作用

  • 前期大学习率：快速更新参数，让模型"大步"找最优方向；

  • 后期小学习率：慢慢调整，避免"步子太大"跳过最优解，让训练更稳定、精度更高。

3.6.2.2 代码

import torch
import torch.optim as optim
import matplotlib.pyplot as plt

def test_StepLR():
    # 0. 参数初始化
    LR = 0.1  # 设置学习率初始值为0.1，后续会按策略衰减
    iteration = 10  # 每个epoch里的迭代次数（可理解为一批数据分10次更新，模拟batch训练）
    max_epoch = 200  # 最大训练轮数，控制训练时长

    # 1. 初始化参数
    y_true = torch.tensor([10.])  # 真实标签，假设的监督学习目标值
    x = torch.tensor([1.0])  # 输入特征，这里简化为标量1.0
    w = torch.tensor([1.0], requires_grad=True)  # 模型参数（权重），需要计算梯度更新

    # 2. 优化器：用SGD优化器，优化参数w，学习率LR，动量0.9（加速梯度更新）
    optimizer = optim.SGD([w], lr=LR, momentum=0.9)

    # 3. 设置学习率下降策略：StepLR，每step_size=50个epoch，学习率乘以gamma=0.5衰减
    scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)

    # 4. 用于记录学习率和epoch的列表，后续绘图用
    lr_list, epoch_list = list(), list()

    # 5. 训练循环：遍历每个epoch
    for epoch in range(max_epoch):
        # 记录当前epoch的学习率和epoch编号
        lr_list.append(scheduler_lr.get_last_lr())  # 获取并保存当前生效的学习率
        epoch_list.append(epoch)  # 保存当前epoch编号

        # 每个epoch里的小批量迭代（这里简化模拟，实际是遍历数据集的batch）
        for i in range(iteration):
            # 计算损失：简单的平方损失，(w*x - y_true)^2 / 2 ，模拟预测值与真实值的误差
            loss = ((w * x - y_true) ** 2) / 2.0  
            optimizer.zero_grad()  # 清空梯度，避免累加
            loss.backward()  # 反向传播，计算参数w的梯度
            optimizer.step()  # 根据梯度和优化器规则（SGD）更新参数w

        # 一个epoch的参数更新完后，更新下一个epoch的学习率（StepLR策略生效）
        scheduler_lr.step()  

    # 6. 绘制学习率变化曲线
    plt.plot(epoch_list, lr_list, label="Step LR Scheduler")  # 画epoch-学习率曲线
    plt.xlabel("Epoch")  # x轴：训练轮数
    plt.ylabel("Learning rate")  # y轴：学习率
    plt.legend()  # 显示图例
    plt.show()  # 弹出可视化窗口
test_StepLR()

3.6.3 指定间隔学习率衰减

3.6.3.1 概述

• **MultiStepLR（多阶段学习率衰减）的策略说明，核心是按自定义的多个里程碑（milestones）**调整学习率，比等间隔衰减更灵活；

• 核心逻辑：和 StepLR 类似，也是通过 lr = lr * gamma 衰减学习率，但调整时机由自定义的 milestones 控制，而非固定间隔；

• API：

  lr_scheduler.MultiStepLR(optimizer, milestones, gamma=0.1)

  • optimizer：要调整学习率的优化器（如 Adam、SGD ），指定"改谁的学习率"；

  • milestones：自定义的衰减时机 ，是一个列表，每个数值代表"第几个 Epoch 时衰减"。比如 [50,125,160]，就精准控制在这三个节点降学习率；

  • gamma：衰减系数，学习率乘以这个值缩小，比如 0.5 就是每次衰减为原来的 50%，控制衰减幅度；

• 下图展示了学习率随 Epoch 的变化 ：milestones=[50,125,160]，就在第 50、125、160 个 Epoch 时，分别让学习率乘以 gamma 衰减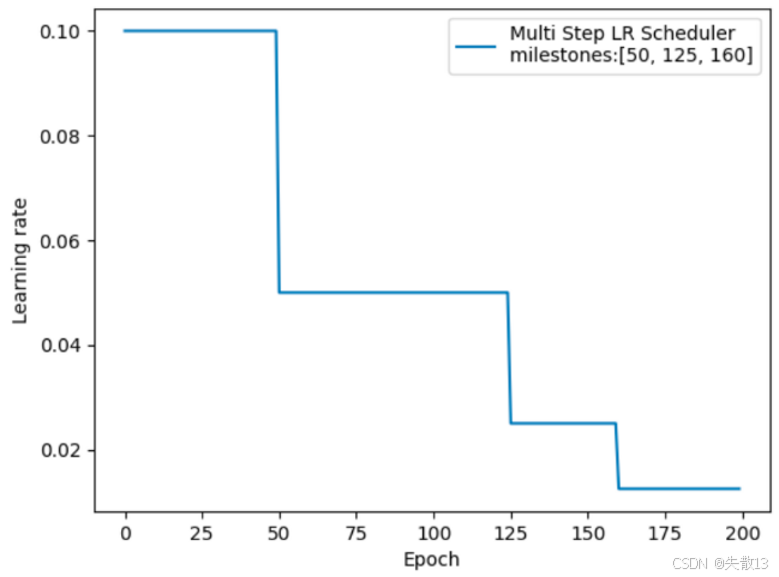

  

  • 0-50 Epoch：学习率保持初始值（如 0.1）；

  • 50 Epoch：触发衰减，学习率乘以 gamma（如变成 0.05）；

  • 125、160 Epoch：再次触发衰减，逐步缩小学习率，适配模型不同阶段的训练需求；

• 对比 StepLR 的优势

  • StepLR 是"固定间隔"衰减（如每 50 Epoch 衰减一次 ），而 MultiStepLR 支持非均匀、自定义时机的衰减；
  • 比如训练中发现"第 125、160 Epoch 是模型收敛的关键节点"，就可以精准在这些位置降学习率，更灵活适配复杂训练需求。

3.6.3.2 代码

import torch
import torch.optim as optim
import matplotlib.pyplot as plt

def test_MultiStepLR():
    # 为PyTorch设置随机种子，确保实验可复现（每次初始化的随机值相同）
    torch.manual_seed(1)  
    
    # 1. 初始化超参数与核心变量
    LR = 0.1  # 初始学习率，控制参数更新的步长
    iteration = 10  # 每个epoch内的迭代次数（可理解为一批数据分10次更新）
    max_epoch = 200  # 最大训练轮数，决定模型训练的总时长
    
    # 初始化模型参数（权重），形状为(1,)，需要计算梯度用于反向传播更新
    weights = torch.randn((1), requires_grad=True)  
    # 定义目标值（标签），形状为(1,)，用于计算损失
    target = torch.zeros((1))  
    
    # 打印初始参数与目标值，方便观察初始状态
    print('weights--->', weights, 'target--->', target)  
    
    # 2. 配置优化器
    # 使用SGD优化器，优化的参数是weights，设置初始学习率LR，动量momentum=0.9（加速梯度更新）
    optimizer = optim.SGD([weights], lr=LR, momentum=0.9)  
    
    # 3. 配置学习率调度器（MultiStepLR）
    # 设定学习率衰减的里程碑（在哪些epoch时衰减）
    milestones = [50, 125, 160]  
    # 初始化MultiStepLR调度器：在milestones指定的epoch处，学习率乘以gamma=0.5衰减
    scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.5)  
    
    # 初始化两个列表，用于记录每个epoch的学习率和对应的epoch编号
    lr_list, epoch_list = list(), list()  

    # 4. 训练循环（核心逻辑）
    # 遍历每个训练轮数epoch（从0到max_epoch-1）
    for epoch in range(max_epoch):  
        # 记录当前epoch的学习率（get_last_lr()获取调度器当前生效的学习率）
        lr_list.append(scheduler_lr.get_last_lr())  
        # 记录当前的epoch编号，用于后续绘图
        epoch_list.append(epoch)  

        # 每个epoch内的小批量迭代（模拟分批次训练）
        for i in range(iteration):  
            # 计算损失：(weights - target)^2 ，这里用torch.pow实现平方运算
            loss = torch.pow((weights - target), 2)  
            # 清空优化器已有的梯度（避免梯度累加影响计算）
            optimizer.zero_grad()  
            # 反向传播：自动计算损失对可训练参数（weights）的梯度
            loss.backward()  
            # 根据梯度更新参数（执行一次参数更新步骤）
            optimizer.step()  

        # 一个epoch的参数更新完成后，更新学习率（触发调度器逻辑，判断是否需要衰减）
        scheduler_lr.step()  

    # 5. 可视化学习率变化
    # 绘制epoch与学习率的关系曲线，label中展示调度器类型和里程碑信息
    plt.plot(epoch_list, lr_list, label=f"Multi Step LR Scheduler\nmilestones: {milestones}")  
    # 设置x轴标签为"Epoch"，表示横轴是训练轮数
    plt.xlabel("Epoch")  
    # 设置y轴标签为"Learning rate"，表示纵轴是学习率
    plt.ylabel("Learning rate")  
    # 显示图例（展示曲线的含义）
    plt.legend()  
    # 显示绘制的图像（弹出窗口展示学习率变化曲线）
    plt.show()  

test_MultiStepLR()

3.6.4 按指数学习率衰减

3.6.4.1 概述

• 指数学习率衰减（Exponential LR Scheduler），核心是让学习率随训练轮次（Epoch）按指数规律下降，实现更细腻的训练节奏控制；

• 调整方式是 lr = lr * (gamma ^ epoch) ，关键理解：

  • gamma 是指数的"底"，必须小于 1 （比如 0.95、0.9 ），这样随着 epoch 增大，gamma^epoch 会指数级缩小，带动学习率 lr 指数衰减；

  • 和 StepLR（阶梯式跳变）不同，指数衰减是"连续、平滑"的下降，学习率每一轮都在变小，而非到固定节点才突变；

• API

  lr_scheduler.ExponentialLR(optimizer, gamma)

  • optimizer：要调整学习率的优化器（如 Adam、SGD），指定"改谁的学习率"；

  • gamma：指数底数，控制衰减速度。比如 gamma=0.95，每过 1 个 Epoch，学习率乘以 0.95；gamma 越小，衰减越快（曲线下降越陡）；

• 下面的折线图直观展示学习率随 Epoch 的变化：

  

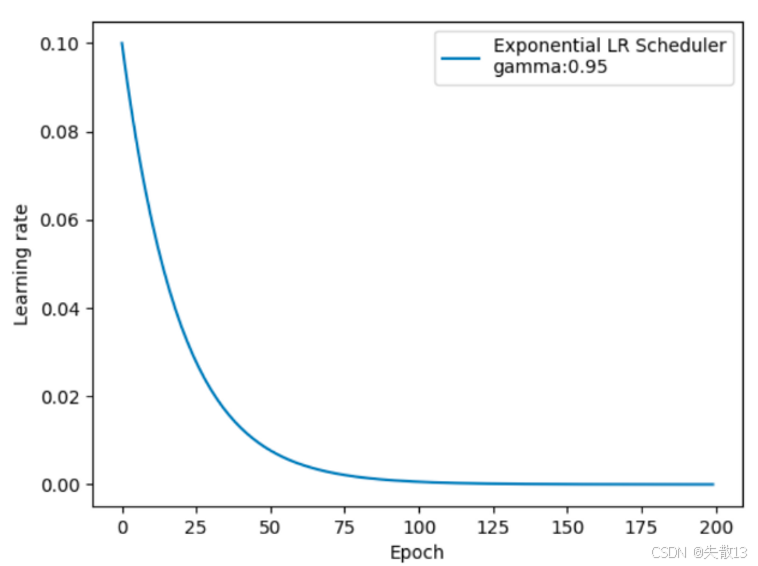
  • 初始学习率较高（比如 0.1），随着 Epoch 增加，学习率按 gamma^epoch 指数缩小；

  • 前期下降快（因为指数函数前期斜率大），后期逐渐趋于平缓（逼近 0 但不会到 0），适配模型训练"先快后慢"的需求；

• 对比其他衰减策略

  策略	特点	适用场景
  指数衰减（Exponential）	连续、平滑指数下降	希望学习率细腻衰减，避免突变
  等间隔衰减（StepLR）	阶梯式跳变衰减	需要明确分段调整的场景
  多阶段衰减（MultiStepLR）	自定义里程碑跳变衰减	精准控制特定 Epoch 衰减

• 指数衰减的优势是学习率变化更平滑 ，不会像阶梯衰减那样"突变"，适合追求细腻训练节奏的场景（比如对学习率敏感的模型）；但缺点是衰减速度由 gamma 固定，不像 MultiStepLR 能灵活自定义衰减时机。

3.6.4.2 代码

import torch
import torch.optim as optim
import matplotlib.pyplot as plt

def test_ExponentialLR():
    # 0. 参数初始化
    # 设置初始学习率，控制参数更新的步长
    LR = 0.1  
    # 每个epoch内的迭代次数（一批数据分10次更新，模拟小批量训练）
    iteration = 10  
    # 最大训练轮数，决定模型训练的总时长
    max_epoch = 200  

    # 1. 初始化模型相关参数
    # 真实标签（目标值），用于计算损失
    y_true = torch.tensor([10.])  
    # 输入特征，形状为[1.0]，用于模型计算
    x = torch.tensor([1.0])  
    # 模型参数（权重），形状为[1.0]，需要计算梯度更新
    w = torch.tensor([1.0], requires_grad=True)  

    # 2. 配置优化器
    # 使用SGD优化器，优化参数w，设置初始学习率LR，动量momentum=0.9（加速梯度更新）
    optimizer = optim.SGD([w], lr=LR, momentum=0.9)  

    # 3. 配置指数学习率调度器（ExponentialLR）
    # 指数衰减的底数gamma，控制衰减速度（gamma越小，衰减越快）
    gamma = 0.95  
    # 初始化ExponentialLR调度器：学习率按 lr = lr * (gamma ^ epoch) 衰减
    scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)  

    # 4. 初始化记录列表
    # 用于保存每个epoch的学习率
    lr_list, epoch_list = list(), list()  

    # 5. 训练循环（核心逻辑）
    # 遍历每个训练轮数epoch（从0到max_epoch-1）
    for epoch in range(max_epoch):  
        # 记录当前epoch的学习率（get_last_lr()获取调度器当前生效的学习率）
        lr_list.append(scheduler_lr.get_last_lr())  
        # 记录当前的epoch编号，用于后续绘图
        epoch_list.append(epoch)  

        # 每个epoch内的小批量迭代（模拟分批次训练）
        for i in range(iteration):  
            # 计算损失：(w*x - y_true)^2 / 2 ，用均方误差衡量预测值与真实值的差异
            loss = ((w * x - y_true) ** 2) / 2.0  
            # 清空优化器已有的梯度（避免梯度累加影响计算）
            optimizer.zero_grad()  
            # 反向传播：自动计算损失对可训练参数（w）的梯度
            loss.backward()  
            # 根据梯度更新参数（执行一次参数更新步骤）
            optimizer.step()  

        # 一个epoch的参数更新完成后，更新学习率（触发指数衰减逻辑）
        scheduler_lr.step()  

    # 6. 可视化学习率变化曲线
    # 绘制epoch与学习率的关系曲线，label标识为"Exponential LR Scheduler"
    plt.plot(epoch_list, lr_list, label="Exponential LR Scheduler")  
    # 设置x轴标签为"Epoch"，表示横轴是训练轮数
    plt.xlabel("Epoch")  
    # 设置y轴标签为"Learning rate"，表示纵轴是学习率
    plt.ylabel("Learning rate")  
    # 显示图例（展示曲线的含义）
    plt.legend()  
    # 显示绘制的图像（弹出窗口展示学习率变化曲线）
    plt.show()  

test_ExponentialLR()