Ⅳ人工智能机器学习之监督学习的概述

1.概述

机器学习的定义：

1.Arthur Samuel的定义：在没有明确设置的情况下使计算机具有学习能力的研究领域。

2.Tom Mitchell的定义：计算机程序从经验E中学习，解决某一任务T，进行某一性能度量P，通过P测定在T上的表现因经验E而提高。

专业术语解析：

监督学习：「学习输入到输出的映射函数」，你可以把它理解为：模型通过 "老师"（标签 Y）的指导，学会从 "题目"（输入 X）中找到 "答案"（Y）的规律，之后遇到新题目时能独立给出答案。

回归(Regression)：我们预测的目标是预测连续值的输出。

分类(Classification):我们预测的目标是预测离散值输出。

回归：标签是连续值（如房价、温度、销量），模型输出是一个数值。
分类：标签是离散值（如 0/1、猫 / 狗、A/B/C 类），模型输出是一个类别。

无监督学习：挖掘数据自身的内在结构」。你可以把它理解为：模型没有 "老师"（无标签），只能自己观察数据的 "特征"（如相似度、分布），总结出数据的规律（比如哪些样本长得像、数据的核心特征是什么）。

聚类任务（如 K-Means）：目标是将数据分成 K 个簇，使得同一簇内的样本相似度高（类内距离小），不同簇的样本相似度低（类间距离大）
降维任务（如 PCA）：目标是将高维特征 X 映射到低维空间，保留数据的核心信息（方差最大）。数学上通过求解协方差矩阵的特征值和特征向量，选取前 k 个最大特征值对应的特征向量作为投影矩阵。

复制代码

机器学习学习范式
├─ 监督学习（有标签，学X→Y映射）
│  ├─ 回归（Y连续：房价、温度）
│  └─ 分类（Y离散：猫/狗、垃圾邮件）
├─ 无监督学习（无标签，学X内在结构）
│  ├─ 聚类（分组：用户群体、商品分类）
│  ├─ 降维（压缩：PCA、图像特征压缩）
│  └─ 异常检测（找异常：欺诈交易、故障设备）
├─ 半监督学习（部分标签，结合两者优势）
└─ 强化学习（无标签，通过奖励试错学习）

2.监督学习

2.1监督学习完整的的解决思路：

1.明确目标：

⭐明确 "已知输入（X）→ 要预测的输出（y）"，判断是否为监督学习（是否有标签 y），并细分任务类型

回归任务（y 是连续值，如房价、温度）；

分类任务（y 是离散标签，如垃圾邮件识别、疾病诊断）；

序列任务（y 是序列，如文本翻译、语音转文字，本质是监督学习的延伸）。

2.数据探索(EDA):

⭐基于问题定义，分析已有数据集的基本情况(pandas/ matplotlib**)，为后续预处理和建模打基础**

样本层面：样本数量（是否足够？太少可能过拟合）、是否有重复样本 / 异常样本（如房价为负数）。

特征层面：特征类型（数值型如面积、类别型如地段）、特征维度（是否高维？如图片像素）、是否有缺失值（如部分房屋未记录房龄）。

标签层面：标签分布（回归是否正态分布？分类是否均衡？如二分类中 90% 是正例，10% 是负例）。

3.数据预处理：

⭐解决数据探索中发现的问题，将原始数据转化为 "干净、规范" 的特征矩阵（X）和标签向量（y）

缺失值处理：缺失值处理：数值型特征用 "均值 / 中位数填充"，类别型特征用 "众数填充" 或 "新增'缺失'类别"；

异常值处理：删除极端异常值（如 3σ 之外），或用 "分位数替换"（如用 99% 分位数替换超过该值的异常值）；

特征编码：类别型特征→数值型（如地段 "北京"→1、"上海"→2，或用独热编码）；

特征缩放：数值型特征标准化（StandardScaler）或归一化（MinMaxScaler）（避免如 "面积（0-1000）" 和 "房龄（0-50）" 因量级差异影响模型）；

特征选择 / 降维：删除冗余特征（如 "身高" 和 "体重" 高度相关，保留一个），高维数据用 PCA 降维（如图片数据）。

4.划分数据集：

⭐将预处理后的数据集分成 3 部分（避免 "用训练数据测试模型" 导致的过拟合误判）

训练集（Train Set，70%-80%）：用于模型训练（学习参数）；

验证集（Validation Set，10%-15%）：用于超参数调优（如学习率、树的深度）；

测试集（Test Set，10%-15%）：用于最终评估（模拟模型在真实场景的表现，只能用一次）。

5.模型选择：设计 "f (x)------ 输入到输出的映射关系"：

⭐根据 "问题类型 + 数据特点" 选择合适的模型（从简单到复杂）

回归任务：线性回归（简单、可解释）→ 决策树回归（处理非线性）→ 随机森林回归（集成模型，精度更高）→ XGBoost/LightGBM（工业界常用，兼顾精度和效率）；

线性回归：f(x) = w₀ + w₁x₁ + w₂x₂ + ... + wₙxₙ（w 是参数，x 是特征）；

分类任务：逻辑回归（简单、可解释）→ 决策树分类→ 支持向量机（SVM，高维数据表现好）→ 神经网络（复杂任务如图像分类）。

f(x) = σ(w₀ + w₁x₁ + ... + wₙxₙ)（σ 是 sigmoid 函数，输出概率）

6.构造损失函数：定义 "模型预测错了多少"（优化的目标）：

⭐设计一个 "衡量预测值ŷ与真实标签 y 差距" 的函数 L (ŷ, y)，损失函数越小，模型预测越准。需根据任务类型选择。

回归问题选择：均方差（MSE）

分类问题选择：交叉熵损失（Cross Entropy）

7.求解参数：找到 "使损失函数最小的 w"

⭐通过优化算法求解参数 w，使损失函数 L (ŷ, y) 最小。

梯度下降算法进行计算

8.模型评估：判断 "模型好不好用"

⭐用测试集计算模型的评估指标（避免用训练集评估，因为训练集上的误差可能是 "过拟合" 导致的）

回归任务：均方根误差（RMSE，MSE 开平方，和 y 同量级，易理解）、决定系数（R²，越接近 1 越好，衡量模型解释力）；

分类任务：准确率（Accuracy，简单但对不平衡数据不友好）、精确率（Precision）、召回率（Recall）、F1 分数（兼顾精确率和召回率）、ROC-AUC（二分类常用，抗不平衡数据）。

判断标准：如果测试集指标远低于训练集指标→过拟合（需正则化、增加数据）；如果训练集和测试集指标都低→欠拟合（需换复杂模型、增加特征）。

9. 模型优化：提升 "模型性能"（迭代过程）

⭐核心任务：根据评估结果调整模型，直到满足业务需求

欠拟合优化：换更复杂的模型（如线性回归→随机森林）、增加特征（如房屋数据中加入 "周边学校数量"）；

过拟合优化：正则化（如线性回归加 L1/L2 正则）、减少特征、增加训练数据、集成学习（如随机森林用多棵树投票）；

超参数调优：用网格搜索（GridSearch）、随机搜索（RandomizedSearch）调整超参数（如学习率、树的深度）。

10.模型部署：落地 "实际应用"（监督学习的最终目标）

⭐核心任务：将训练好的模型封装成接口（如 REST API），供业务系统调用（如房价预测接口嵌入房产 APP）。

用 Python 的pickle/joblib保存模型，用Flask/FastAPI搭建接口，用Docker容器化部署。

2.2线性回归+逻辑回归(分类问题)

1.常见参数说明：

|-----------------|-----------------|
| h(x) | hypothesis 假设函数 |
| m | 训练集样本数量 |
| x | 自变量x,特征值 |
| y | 因变量y,标签值 |
| (x,y) | 一个训练样本 |
| (x^(i),y^(i)) | 第i个训练样本 |
[常见参数说明]

概念剖析：

回归函数的算法模型选择：

思路：数据集->算法选择->模型函数选择->损失函数选择

任务类型模型函数（核心形式）常用损失函数关键备注

单变量线性回归 y = kx + b（线性模型） MSE（均方误差）输入特征仅 1 个，输出连续值

多变量线性回归 y = w_1x_1 + ... + w_nx_n + b（线性模型） MSE 输入特征多个，输出连续值

二分类逻辑回归 y_pred = sigma(w * x + b)(线性 + sigmoid）二分类交叉熵（BCE）输出是类别 1 的概率（0~1）

多分类逻辑回归 y_{pred,i} = softmax(w_i * x + b)（线性 + softmax）多分类交叉熵输出是各类别概率（和为 1）

代价函数 = 损失函数在全体样本上的汇总（通常是平均值或总和） 。

概念计算对象核心作用与另一个概念的关系

损失函数（Loss）单个样本衡量「一个样本」的预测误差代价函数是损失函数的 "平均 / 总和"

代价函数（Cost）全体样本 / 批量样本衡量「整个数据集」的预测误差是优化目标（训练时最小化的函数）

任务类型	模型函数（核心形式）	常用损失函数	关键备注
单变量线性回归	y = kx + b（线性模型）	MSE（均方误差）	输入特征仅 1 个，输出连续值
多变量线性回归	y = w_1x_1 + ... + w_nx_n + b（线性模型）	MSE	输入特征多个，输出连续值
二分类逻辑回归	y_pred = sigma(w * x + b)(线性 + sigmoid）	二分类交叉熵（BCE）	输出是类别 1 的概率（0~1）
多分类逻辑回归	y_{pred,i} = softmax(w_i * x + b)（线性 + softmax）	多分类交叉熵	输出是各类别概率（和为 1）

概念	计算对象	核心作用	与另一个概念的关系
损失函数（Loss）	单个样本	衡量「一个样本」的预测误差	代价函数是损失函数的 "平均 / 总和"
代价函数（Cost）	全体样本 / 批量样本	衡量「整个数据集」的预测误差	是优化目标（训练时最小化的函数）

2.3代价函数(Cost Function)

本质：一个模型的量化指标，预测值和真实值之间误差的"总概括"，是衡量模型性能好坏的"标尺"

Hypothesis:(假设函数)

hθ(x) = θ₀+θ₁x

Parameters:(参数)

θ₀,θ₁

Cost Function:(代价函数)

Goal:(目标)

minimize J(θ₀,θ₁)

回归问题最常用的代价函数：均方误差(MSE)

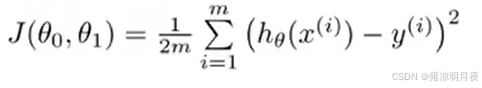
平方项 [h_θ(xᵢ)-yᵢ]²：

保证误差非负（不管预测值比真实值大还是小，平方后都是正的，总和不会抵消）；

对大误差 "惩罚更重"（比如误差 2 和误差 4，平方后是 4 和 16，突出了大误差的影响，让模型更关注修正严重错误）。

1/m：对所有样本的误差取平均值（避免样本数量 m 影响代价函数的大小，比如 1000 个样本的总误差肯定比 10 个样本大，取平均后更易横向对比）；

1/2：是为了后续求导方便（平方项求导后会出现系数 2，乘以 1/2 后可以抵消，让梯度表达式更简洁，不影响最小值的位置）。

分类问题最常用的代价函数：交叉熵(Cross-Entropy)

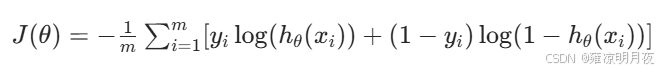
逻辑回归的预测值是 h_θ(x) = σ(θ₀+θ₁x)（σ 是 sigmoid 函数，输出在 0~1 之间，代表 "属于 1 类" 的概率）。

公式拆解（核心逻辑）

当 yᵢ=1（真实是 1 类）：第二项 (1-yᵢ) log (...) 为 0，代价函数简化为 -log (h_θ(xᵢ))。h_θ(xᵢ) 越接近 1（预测越准），log 值越接近 0，代价越小；h_θ(xᵢ) 越接近 0（预测错误），log 值越负，代价越大（惩罚越重）。

当 yᵢ=0（真实是 0 类）：第一项 yᵢlog (...) 为 0，代价函数简化为 -log (1-h_θ(xᵢ))。h_θ(xᵢ) 越接近 0（预测越准），代价越小；越接近 1（预测错误），代价越大。

总结：

本章节主要学习了关于机器学习的基础定义，以及常见的监督学习和无监督学习的区分以及相关的知识点，并简单概括了监督学习的解题思路，以及线性回归和逻辑回归的相关知识，以及更深层次的代价函数的使用和标准。为后续的实际运用奠定基础。