本文我们将一起学习二叉搜索树。如果想了解更多关于二叉树等数据结构的相关知识,请移步主页进行查找,万分感谢你的阅读。
1.二叉搜索树的基础
1.1二叉搜索树的概念
二叉搜索树又称二叉排序树 ,具有以下性质:
1)若它的左子树不为空,左子树上的所有节点值都小于根节点值。
2)若它的右子树不为空,右子树上的所有节点值都大于根节点值。
3)它的左右子树也都是二叉搜索树。
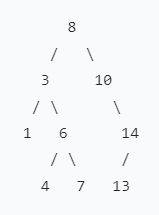
图中给出的二叉树就是一个二叉搜索树。
注意 :容器底层是二叉搜索树的map和set不支持插入相等的节点值,而同样底层容器为二叉搜索树的multimap和multiset是支持插入相等值的。
1.2效率分析
设二叉搜索树的节点数为N,平衡状态下其高度为log 2(N) ,因为在平衡状态下左右子树高度差不多,对树增删改查的效率为O(log N) 。但在一些极端情况下 ,例如插入的数据是有序的,导致二叉树退化成单支或类似单支的结构,导致其效率变为O(N)。
为了解决这种问题的发生,我们在实际使用的时候常采用AVL树或者红黑树(平衡二叉搜索树),通过其特有的旋转机制维持平衡,确保O(log N)的效率稳定。可在个人主页查看具体知识讲解。
2.二叉树的结构及其操作实现
2.1二叉搜索树节点的数据结构
cpp
template <class K>
struct BSTNode
{
K _key;
BSTNode<K>* _left;
BSTNode<K>* _right;
BSTNode(const K& key)
;_key(key)
,_left(nullptr)
,_right(nullptr)
{}
};2.2 二叉搜索树的插入
**BST树插入过程的本质是寻找第一个空的叶子节点位置。**如果树为空,则直接新增节点,赋值给_root指针;树不为空,按二叉搜索树的性质,遵循左大右小原则,新节点的值小于当前节点则插入到左子树,大于则插入大到右子树,且不允许插入重复值。
具体的函数实现代码如下:
cpp
bool Insert(const K& key)
{
if(_root == nullptr)
{
_root=new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur=_root;
while(cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur=new Node(key);
if(parent->_key < key)
{
parent->right = cur;
}
else
{
parent->_left = cur;
}
return true;
}上述代码即为二叉搜索树插入的实现。具体的实现过程分为:判断是否为空树;在while循环后找到cur正确位置的父节点;再通过与父节点的大小比较确定叶节点位置。
2.3二叉搜索树的查找
二叉搜索树的查找原理和插入相似。都是通过一层一层查找到正确位置。
代码实现如下:
cpp
bool Find(const K& key)
{
Node* cur=_root;
while(cur)
{
if(cur->_key > key)
{
cur = cur->left;
}
else if(cur->_key < key)
{
cur = cur->right;
}
else
{
return true;
}
}
return false;
}二叉搜索树的查找就是插入代码中查找的内部分,最多就查高度次,走到空,还没找到,这个值就不存在。
2.4二叉搜索树的删除
删除之前首先查找元素是否存在,如果不存在,直接返回false。
如果存在的话,该节点的位置有四种可能 :
1) 该节点左右子节点都为空;
2) 该节点左节点为空,右节点不为空;
3) 该节点右节点为空,左节点不为空;
**4)**该节点左右节点都不为空。
具体解决问题代码如下:
cpp
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else {
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
return true;
}
else if(cur->_right==nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
return true;
}
else//这个就是节点左右节点都存在,采用替换法
{
Node* rightMinP = cur;//最小值节点的父节点
Node* rightMin = cur->_right;//从右子树开始查找
while (rightMin->_left)//循环找到最左侧节点
{
rightMinP = rightMin;
rightMin = rightMin->_left;
}
cur->_key = rightMin->_key;//值的转移
if (rightMinP->_left == rightMin)//最小值节点是父节点的左孩子
{
rightMinP->_left = rightMin->_right;
}
else//最小值节点是父节点的有孩子(特殊情况)
{
rightMinP->_right = rightMin->_right;
}
delete rightMin;
return true;
}
}
}
return false;
}前三种情况较为简单,重点讲解第四个情况 ,就是左右节点都存在的情况。
核心思路 就是找到待删除节点右子树中值最小的节点(即右子树中最左侧的节点) ,用这个最小值节点的值替换待删除节点的值,最后删除这个节点。这个替代法充分利用了BST的特性结构,在保证删除操作后,二叉搜索树的特性任然存在。
3.类私有工具函数
3.1中序遍历
cpp
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}3.2复制树
cpp
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newRoot = new Node(root->_key, root->_value);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}3.3销毁树
cpp
void Destroy(Node* root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}这三个函数通常被设计为二叉搜索树类的私有成员函数 ,主要是它们的参数需要直接操作底层节点指针,而节点指针属于类的内部实现细节。对外只暴露安全的公共接口,防止被误用。
总结,本节内容主要学习了二叉搜索树的相关概念和操作,对后面学习平衡二叉树(红黑树和AVL树)打下坚实基础。如果你发现文中出现某个错误,希望你能帮忙指出来,万分感谢!希望我们共同进步!