【数据结构】最短路径的求解

2401_841495642025-12-23 15:09

目录

一、习题描述

二、习题解答

[（1）迪杰斯特拉算法（求顶点 A 到其他顶点的最短路径）](#（1）迪杰斯特拉算法（求顶点 A 到其他顶点的最短路径）)

初始化

[步骤 1：处理源点 A 的出边（A→B (3)、A→C (6)）](#步骤 1：处理源点 A 的出边（A→B (3)、A→C (6)）)

[步骤 2：处理顶点 B 的出边（B→C (2)、B→D (6)）](#步骤 2：处理顶点 B 的出边（B→C (2)、B→D (6)）)

[步骤 3：处理顶点 C 的出边（C→D (5)、C→E (4)）](#步骤 3：处理顶点 C 的出边（C→D (5)、C→E (4)）)

[步骤 4：处理顶点 D 的出边（D→E (2)、D→F (2)）](#步骤 4：处理顶点 D 的出边（D→E (2)、D→F (2)）)

[步骤 5：处理顶点 E 的出边（E→F (3)）](#步骤 5：处理顶点 E 的出边（E→F (3)）)

[最终结果（A 到各顶点）](#最终结果（A 到各顶点）)

Python代码：

程序运行结果展示：

（2）弗洛伊德算法（求所有顶点对的最短路径）

初始距离矩阵（∞表示无直接路径）

[步骤 1：以 A 为中间顶点（k=A）](#步骤 1：以 A 为中间顶点（k=A）)

[步骤 2：以 B 为中间顶点（k=B）](#步骤 2：以 B 为中间顶点（k=B）)

[步骤 3：以 C 为中间顶点（k=C）](#步骤 3：以 C 为中间顶点（k=C）)

[步骤 4：以 D 为中间顶点（k=D）](#步骤 4：以 D 为中间顶点（k=D）)

[步骤 5：以 E、F 为中间顶点](#步骤 5：以 E、F 为中间顶点)

最终所有顶点对的最短路径长度（仅展示存在路径的情况）

Python代码：

程序运行结果展示：

（3）迪杰斯特拉算法与弗洛伊德算法的区别

三、总结

一、习题描述

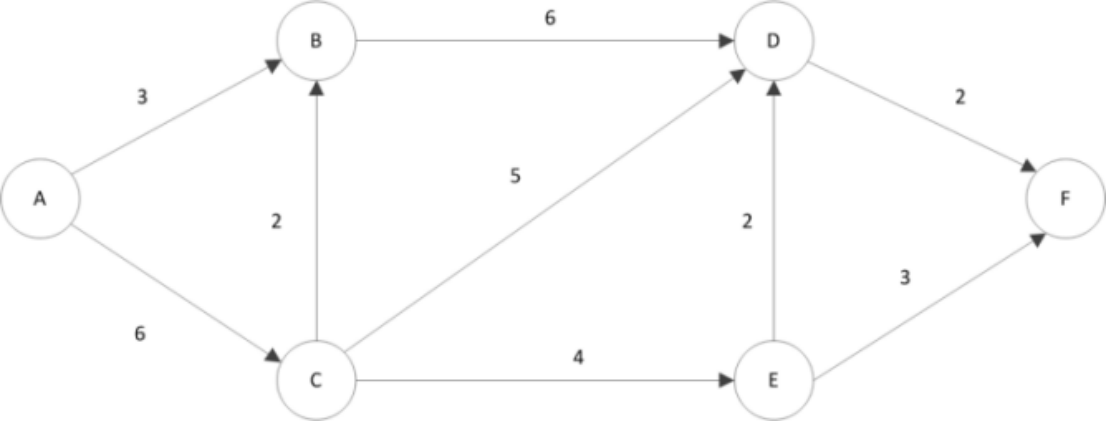
有向网如图所示，请回答下面问题。

  1. 利用迪杰斯特拉算法求出从顶点A到其他各顶点的最短路径及其路径长度在求解过程中的变化。
  2. 利用弗洛伊德算法求出每一对顶点之间的最短路径及其路径长度在求解过程中的变化。
  3. 写出迪杰斯特拉算法和弗洛伊德算法的区别。

二、习题解答

（1）迪杰斯特拉算法（求顶点 A 到其他顶点的最短路径）

迪杰斯特拉算法是单源最短路径算法，以 A 为源点，通过 "选当前最近顶点→松弛邻接边→更新距离" 的步骤求解，过程如下：

初始化
  • 距离数组 dist（记录 A 到各顶点的距离）：dist = [0, ∞, ∞, ∞, ∞, ∞]（对应顶点 A,B,C,D,E,F）
  • 前驱数组 prev（记录路径的前驱顶点）：prev = [-1, -1, -1, -1, -1, -1]
  • 已确定最短路径的顶点集合 S = {A}
步骤 1：处理源点 A 的出边（A→B (3)、A→C (6)）
  • 更新 dist[B] = 3（prev[B] = A），dist[C] = 6（prev[C] = A）
  • 未确定顶点中dist最小的是 B，将 B 加入S（S = {A,B}）
  • 当前dist：[0, 3, 6, ∞, ∞, ∞]
步骤 2：处理顶点 B 的出边（B→C (2)、B→D (6)）
  • 候选距离：B→C为3+2=5（小于原dist[C]=6）→ 更新dist[C] = 5，prev[C] = B
  • 候选距离：B→D为3+6=9（小于原dist[D]=∞）→ 更新dist[D] = 9，prev[D] = B
  • 未确定顶点中dist最小的是 C，将 C 加入S（S = {A,B,C}）
  • 当前dist：[0, 3, 5, 9, ∞, ∞]
步骤 3：处理顶点 C 的出边（C→D (5)、C→E (4)）
  • 候选距离：C→D为5+5=10（大于原dist[D]=9）→ 不更新
  • 候选距离：C→E为5+4=9（小于原dist[E]=∞）→ 更新dist[E] = 9，prev[E] = C
  • 未确定顶点中dist最小的是 D，将 D 加入S（S = {A,B,C,D}）
  • 当前dist：[0, 3, 5, 9, 9, ∞]
步骤 4：处理顶点 D 的出边（D→E (2)、D→F (2)）
  • 候选距离：D→E为9+2=11（大于原dist[E]=9）→ 不更新
  • 候选距离：D→F为9+2=11（小于原dist[F]=∞）→ 更新dist[F] = 11，prev[F] = D
  • 未确定顶点中dist最小的是 E，将 E 加入S（S = {A,B,C,D,E}）
  • 当前dist：[0, 3, 5, 9, 9, 11]
步骤 5：处理顶点 E 的出边（E→F (3)）
  • 候选距离：E→F为9+3=12（大于原dist[F]=11）→ 不更新
  • 将 F 加入S（S = {A,B,C,D,E,F}）
最终结果（A 到各顶点）
顶点 最短路径长度 路径
B 3 A→B
C 5 A→B→C
D 9 A→B→D
E 9 A→B→C→E
F 11 A→B→D→F
Python代码：
python 复制代码 
def dijkstra(graph, start_idx, vertices):
    n = len(graph)
    dist = [float('inf')] * n  # 起点到各顶点的距离
    dist[start_idx] = 0
    prev = [-1] * n  # 前驱顶点，用于构建路径
    visited = [False] * n  # 已确定最短路径的顶点
    process = []  # 记录过程
    process.append(("初始状态", dist.copy()))

    for _ in range(n):
        # 选未访问的距离最小的顶点
        min_dist, u = float('inf'), -1
        for i in range(n):
            if not visited[i] and dist[i] < min_dist:
                min_dist, u = dist[i], i
        if u == -1: break  # 无可达顶点
        visited[u] = True
        process.append((f"选择顶点{vertices[u]}", dist.copy()))

        # 松弛操作：更新邻接顶点的距离
        for v in range(n):
            if not visited[v] and graph[u][v] != float('inf'):
                if dist[v] > dist[u] + graph[u][v]:
                    dist[v] = dist[u] + graph[u][v]
                    prev[v] = u
                    process.append((f"更新顶点{vertices[v]}的距离为{dist[v]}", dist.copy()))

    # 构建路径
    paths = {}
    for v in range(n):
        if dist[v] == float('inf'):
            paths[vertices[v]] = ("不可达", float('inf'))
        else:
            path = []
            current = v
            while current != -1:
                path.append(vertices[current])
                current = prev[current]
            path.reverse()
            paths[vertices[v]] = (path, dist[v])
    return process, paths


# 初始化图（顶点：A=0,B=1,C=2,D=3,E=4,F=5）
vertices = ['A', 'B', 'C', 'D', 'E', 'F']
INF = float('inf')
graph = [
    [0, 3, 6, INF, INF, INF],  # A
    [INF, 0, 2, 6, INF, INF],  # B
    [INF, INF, 0, 5, 4, INF],  # C
    [INF, INF, INF, 0, 2, 2],  # D
    [INF, INF, INF, INF, 0, 3],  # E
    [INF, INF, INF, INF, INF, 0]  # F
]

# 执行迪杰斯特拉
process, paths = dijkstra(graph, 0, vertices)

# 输出过程
print("（1）迪杰斯特拉算法求解过程：")
for step in process:
    print(f"{step[0]}: 距离数组（A,B,C,D,E,F）={step[1]}")

# 输出最终结果
print("\n从A到各顶点的最短路径及长度：")
for v in vertices:
    path, length = paths[v]
    print(f"A→{v}：路径{path}，长度{length}")
程序运行结果展示：
bash 复制代码 
（1）迪杰斯特拉算法求解过程：
初始状态: 距离数组（A,B,C,D,E,F）=[0, inf, inf, inf, inf, inf]
选择顶点A: 距离数组（A,B,C,D,E,F）=[0, inf, inf, inf, inf, inf]
更新顶点B的距离为3: 距离数组（A,B,C,D,E,F）=[0, 3, inf, inf, inf, inf]
更新顶点C的距离为6: 距离数组（A,B,C,D,E,F）=[0, 3, 6, inf, inf, inf]
选择顶点B: 距离数组（A,B,C,D,E,F）=[0, 3, 6, inf, inf, inf]
更新顶点C的距离为5: 距离数组（A,B,C,D,E,F）=[0, 3, 5, inf, inf, inf]
更新顶点D的距离为9: 距离数组（A,B,C,D,E,F）=[0, 3, 5, 9, inf, inf]
选择顶点C: 距离数组（A,B,C,D,E,F）=[0, 3, 5, 9, inf, inf]
更新顶点E的距离为9: 距离数组（A,B,C,D,E,F）=[0, 3, 5, 9, 9, inf]
选择顶点D: 距离数组（A,B,C,D,E,F）=[0, 3, 5, 9, 9, inf]
更新顶点F的距离为11: 距离数组（A,B,C,D,E,F）=[0, 3, 5, 9, 9, 11]
选择顶点E: 距离数组（A,B,C,D,E,F）=[0, 3, 5, 9, 9, 11]
选择顶点F: 距离数组（A,B,C,D,E,F）=[0, 3, 5, 9, 9, 11]

从A到各顶点的最短路径及长度：
A→A：路径['A']，长度0
A→B：路径['A', 'B']，长度3
A→C：路径['A', 'B', 'C']，长度5
A→D：路径['A', 'B', 'D']，长度9
A→E：路径['A', 'B', 'C', 'E']，长度9
A→F：路径['A', 'B', 'D', 'F']，长度11

（2）弗洛伊德算法（求所有顶点对的最短路径）

弗洛伊德算法是多源最短路径算法，通过 "以每个顶点为中间点，松弛任意两点的距离" 求解，初始距离矩阵（顶点顺序：A,B,C,D,E,F）及更新过程如下：

初始距离矩阵（∞表示无直接路径）
A B C D E F
A 0 3 6 ∞ ∞ ∞
B ∞ 0 2 6 ∞ ∞
C ∞ ∞ 0 5 4 ∞
D ∞ ∞ ∞ 0 2 2
E ∞ ∞ ∞ ∞ 0 3
F ∞ ∞ ∞ ∞ ∞ 0
步骤 1：以 A 为中间顶点（k=A）

其他顶点到 A 的距离均为∞，矩阵无变化。

步骤 2：以 B 为中间顶点（k=B）

更新规则：dist[i][j] = min(dist[i][j], dist[i][B] + dist[B][j])

  • A→C：min(6, 3+2)=5

  • A→D：min(∞, 3+6)=9

  • 更新后矩阵：

    A B C D E F
    A 0 3 5 9 ∞ ∞
    B ∞ 0 2 6 ∞ ∞
    C ∞ ∞ 0 5 4 ∞
    D ∞ ∞ ∞ 0 2 2
    E ∞ ∞ ∞ ∞ 0 3
    F ∞ ∞ ∞ ∞ ∞ 0
步骤 3：以 C 为中间顶点（k=C）

更新规则：dist[i][j] = min(dist[i][j], dist[i][C] + dist[C][j])

  • A→E：min(∞, 5+4)=9

  • B→E：min(∞, 2+4)=6

  • 更新后矩阵：

    A B C D E F
    A 0 3 5 9 9 ∞
    B ∞ 0 2 6 6 ∞
    C ∞ ∞ 0 5 4 ∞
    D ∞ ∞ ∞ 0 2 2
    E ∞ ∞ ∞ ∞ 0 3
    F ∞ ∞ ∞ ∞ ∞ 0
步骤 4：以 D 为中间顶点（k=D）

更新规则：dist[i][j] = min(dist[i][j], dist[i][D] + dist[D][j])

  • A→F：min(∞, 9+2)=11

  • B→F：min(∞, 6+2)=8

  • C→F：min(∞, 5+2)=7

  • 更新后矩阵：

    A B C D E F
    A 0 3 5 9 9 11
    B ∞ 0 2 6 6 8
    C ∞ ∞ 0 5 4 7
    D ∞ ∞ ∞ 0 2 2
    E ∞ ∞ ∞ ∞ 0 3
    F ∞ ∞ ∞ ∞ ∞ 0
步骤 5：以 E、F 为中间顶点
  • 以 E 为中间顶点：候选距离均大于当前距离，矩阵无变化；
  • 以 F 为中间顶点：F 到其他顶点无路径，矩阵无变化。
最终所有顶点对的最短路径长度（仅展示存在路径的情况）
起点→终点 长度 起点→终点 长度
A→B 3 B→C 2
A→C 5 B→D 6
A→D 9 B→E 6
A→E 9 B→F 8
A→F 11 C→D 5
C→E 4
C→F 7
D→E 2
D→F 2
E→F 3
Python代码：
python 复制代码 
def floyd(graph, vertices):
    n = len(graph)
    # 初始化距离矩阵和路径矩阵
    dist = [row.copy() for row in graph]
    path = [[-1]*n for _ in range(n)]  # path[i][j]是i到j的路径中j的前驱
    for i in range(n):
        for j in range(n):
            if i != j and dist[i][j] != INF:
                path[i][j] = i

    process = []  # 记录过程
    process.append(("初始状态（无中间顶点）", [row.copy() for row in dist]))

    # 以k为中间顶点，更新所有i→j的路径
    for k in range(n):
        for i in range(n):
            for j in range(n):
                if dist[i][k] + dist[k][j] < dist[i][j]:
                    dist[i][j] = dist[i][k] + dist[k][j]
                    path[i][j] = path[k][j]
        process.append((f"以顶点{vertices[k]}为中间顶点", [row.copy() for row in dist]))

    # 构建所有顶点对的路径
    all_paths = {}
    for i in range(n):
        for j in range(n):
            if i == j:
                all_paths[(vertices[i], vertices[j])] = ([vertices[i]], 0)
            elif dist[i][j] == INF:
                all_paths[(vertices[i], vertices[j])] = ("不可达", INF)
            else:
                current = j
                path_ij = []
                while current != -1:
                    path_ij.append(vertices[current])
                    current = path[i][current]
                path_ij.reverse()
                all_paths[(vertices[i], vertices[j])] = (path_ij, dist[i][j])
    return process, all_paths

# 初始化图（顶点：A=0,B=1,C=2,D=3,E=4,F=5）
vertices = ['A', 'B', 'C', 'D', 'E', 'F']
INF = float('inf')
graph = [
    [0, 3, 6, INF, INF, INF],  # A
    [INF, 0, 2, 6, INF, INF],  # B
    [INF, INF, 0, 5, 4, INF],  # C
    [INF, INF, INF, 0, 2, 2],  # D
    [INF, INF, INF, INF, 0, 3],  # E
    [INF, INF, INF, INF, INF, 0]   # F
]

# 执行弗洛伊德
process_floyd, all_paths = floyd(graph, vertices)

# 输出过程
print("\n（2）弗洛伊德算法求解过程：")
for step in process_floyd:
    print(f"\n{step[0]}：")
    print("距离矩阵（行=起点，列=终点）：")
    for row in step[1]:
        print(row)

# 输出最终结果
print("\n所有顶点对的最短路径及长度：")
for (u, v) in all_paths:
    path, length = all_paths[(u, v)]
    print(f"{u}→{v}：路径{path}，长度{length}")
程序运行结果展示：
bash 复制代码 
（2）弗洛伊德算法求解过程：

初始状态（无中间顶点）：
距离矩阵（行=起点，列=终点）：
[0, 3, 6, inf, inf, inf]
[inf, 0, 2, 6, inf, inf]
[inf, inf, 0, 5, 4, inf]
[inf, inf, inf, 0, 2, 2]
[inf, inf, inf, inf, 0, 3]
[inf, inf, inf, inf, inf, 0]

以顶点A为中间顶点：
距离矩阵（行=起点，列=终点）：
[0, 3, 6, inf, inf, inf]
[inf, 0, 2, 6, inf, inf]
[inf, inf, 0, 5, 4, inf]
[inf, inf, inf, 0, 2, 2]
[inf, inf, inf, inf, 0, 3]
[inf, inf, inf, inf, inf, 0]

以顶点B为中间顶点：
距离矩阵（行=起点，列=终点）：
[0, 3, 5, 9, inf, inf]
[inf, 0, 2, 6, inf, inf]
[inf, inf, 0, 5, 4, inf]
[inf, inf, inf, 0, 2, 2]
[inf, inf, inf, inf, 0, 3]
[inf, inf, inf, inf, inf, 0]

以顶点C为中间顶点：
距离矩阵（行=起点，列=终点）：
[0, 3, 5, 9, 9, inf]
[inf, 0, 2, 6, 6, inf]
[inf, inf, 0, 5, 4, inf]
[inf, inf, inf, 0, 2, 2]
[inf, inf, inf, inf, 0, 3]
[inf, inf, inf, inf, inf, 0]

以顶点D为中间顶点：
距离矩阵（行=起点，列=终点）：
[0, 3, 5, 9, 9, 11]
[inf, 0, 2, 6, 6, 8]
[inf, inf, 0, 5, 4, 7]
[inf, inf, inf, 0, 2, 2]
[inf, inf, inf, inf, 0, 3]
[inf, inf, inf, inf, inf, 0]

以顶点E为中间顶点：
距离矩阵（行=起点，列=终点）：
[0, 3, 5, 9, 9, 11]
[inf, 0, 2, 6, 6, 8]
[inf, inf, 0, 5, 4, 7]
[inf, inf, inf, 0, 2, 2]
[inf, inf, inf, inf, 0, 3]
[inf, inf, inf, inf, inf, 0]

以顶点F为中间顶点：
距离矩阵（行=起点，列=终点）：
[0, 3, 5, 9, 9, 11]
[inf, 0, 2, 6, 6, 8]
[inf, inf, 0, 5, 4, 7]
[inf, inf, inf, 0, 2, 2]
[inf, inf, inf, inf, 0, 3]
[inf, inf, inf, inf, inf, 0]

所有顶点对的最短路径及长度：
A→A：路径['A']，长度0
A→B：路径['A', 'B']，长度3
A→C：路径['A', 'B', 'C']，长度5
A→D：路径['A', 'B', 'D']，长度9
A→E：路径['A', 'B', 'C', 'E']，长度9
A→F：路径['A', 'B', 'D', 'F']，长度11
B→A：路径不可达，长度inf
B→B：路径['B']，长度0
B→C：路径['B', 'C']，长度2
B→D：路径['B', 'D']，长度6
B→E：路径['B', 'C', 'E']，长度6
B→F：路径['B', 'D', 'F']，长度8
C→A：路径不可达，长度inf
C→B：路径不可达，长度inf
C→C：路径['C']，长度0
C→D：路径['C', 'D']，长度5
C→E：路径['C', 'E']，长度4
C→F：路径['C', 'D', 'F']，长度7
D→A：路径不可达，长度inf
D→B：路径不可达，长度inf
D→C：路径不可达，长度inf
D→D：路径['D']，长度0
D→E：路径['D', 'E']，长度2
D→F：路径['D', 'F']，长度2
E→A：路径不可达，长度inf
E→B：路径不可达，长度inf
E→C：路径不可达，长度inf
E→D：路径不可达，长度inf
E→E：路径['E']，长度0
E→F：路径['E', 'F']，长度3
F→A：路径不可达，长度inf
F→B：路径不可达，长度inf
F→C：路径不可达，长度inf
F→D：路径不可达，长度inf
F→E：路径不可达，长度inf
F→F：路径['F']，长度0

（3）迪杰斯特拉算法与弗洛伊德算法的区别

维度 迪杰斯特拉算法 弗洛伊德算法
适用场景 单源最短路径（一个源点→所有顶点） 多源最短路径（所有顶点对）
算法思想 贪心策略（选当前最近顶点松弛） 动态规划（通过中间顶点松弛）
时间复杂度 邻接矩阵：O (n²)；邻接表 + 堆：O (m log n) 固定 O (n³)（n 为顶点数）
负权边处理 不能处理（破坏贪心正确性） 可处理负权边，但不能处理负权环
实现复杂度 较简单（维护距离 / 前驱数组） 更简洁（三重循环）

三、总结

本文通过具体例题对比了迪杰斯特拉算法和弗洛伊德算法求解最短路径的过程。迪杰斯特拉算法采用贪心策略，逐步确定单源点到其他顶点的最短路径（时间复杂度O(n²)），但不能处理负权边。弗洛伊德算法通过动态规划求解所有顶点对的最短路径（时间复杂度O(n³)），能处理负权边但不支持负权环。两种算法在适用场景、处理能力和实现方式上存在显著差异：迪杰斯特拉适合单源点问题，弗洛伊德适用于多源点问题且实现更简洁。文中通过完整的Python代码演示了两种算法的具体实现步骤和求解过程。

相关推荐
这猪好帅2 小时前
【算法】动态规划 - 数字三角形模型
算法·动态规划
tgethe2 小时前
Java 数组（Array）笔记：从语法到 JVM 内核
java·数据结构
客梦2 小时前
数据结构-单链表
数据结构
M__332 小时前
动规入门——斐波那契数列模型
数据结构·c++·学习·算法·leetcode·动态规划
kesifan3 小时前
数据结构线性表
数据结构·算法
点云SLAM4 小时前
boost中boost::adjacency_list 与 boost::adjacency_list_traits
数据结构·图论·最大流·boos中图模块·泛型算法·traits 解耦设计·adjacency_list
梦帮科技4 小时前
第二十二篇：AI驱动的工作流优化：性能瓶颈自动检测
数据结构·数据库·人工智能·python·开源·极限编程
夏乌_Wx4 小时前
练题100天——DAY33：种花问题+三个数的最大乘积+子数组最大平均数Ⅰ
数据结构
程序员阿鹏4 小时前
List和Set的区别
java·开发语言·数据结构·后端·list
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）05Labelme从安装到标注：零基础完整指南06CentOS的ISO镜像下载07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题09BongoCat - 跨平台键盘猫动画工具10Multisim使用教程详尽版--(2025最新版)